北师大版九年级数学下册第二章二次函数本章复习课件(共20张PPT)
文档属性
| 名称 | 北师大版九年级数学下册第二章二次函数本章复习课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 19:14:19 | ||
图片预览






文档简介
(共20张PPT)
第 二 章 二次函数
九年级数学 下 BS
章末复习
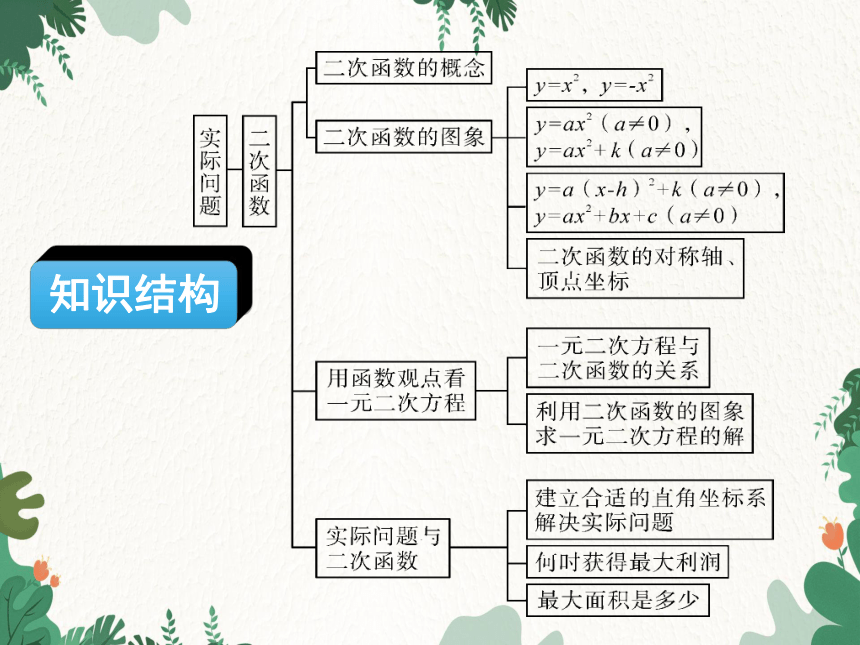
知识结构
1.定义:一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做x的二次函数.
重点解惑
2.填表:
开口向上
开口向上
开口向上
开口向上
开口向上
开口向下
开口向下
开口向下
开口向下
开口向下
y轴
y轴
x=h
x=h
(0,0)
(0,k)
(h,0)
(h,k)
(1)抛物线y=-2x +1的对称轴是 ,顶点坐标是 。
(2)抛物线y=(x-3) -1的最小值是 。
y轴(x=0)
(0,1)
-1
(3)写出一个图象经过原点的二次函数解析式:
。
y=x -2x
(4)抛物线y=-x -2x+3与x轴交于点A( )、
B( ),与y轴交于点C( ),且△ABC的面积为 。
1,0
-3,0
0,3
6
(5)在墙边(足够长)的空地上,准备用36m长的篱笆围一块矩形花圃,问长是多少时,才能使围成的面积最大,最大面积是多少?
解: 设长为xm时 ,面积为y m2
由已知条件得 : y= (36-2x)·x
y= -2(x-9)2+162
∴ 当 x=9 m时, y 的最大面积是162m2
考点一 一元二次方程与二次函数的关系
B
[解析] B 先根据(-7) 2-4k(-7)≥0得到k≥ ,由于是抛物线,所以k≠0.
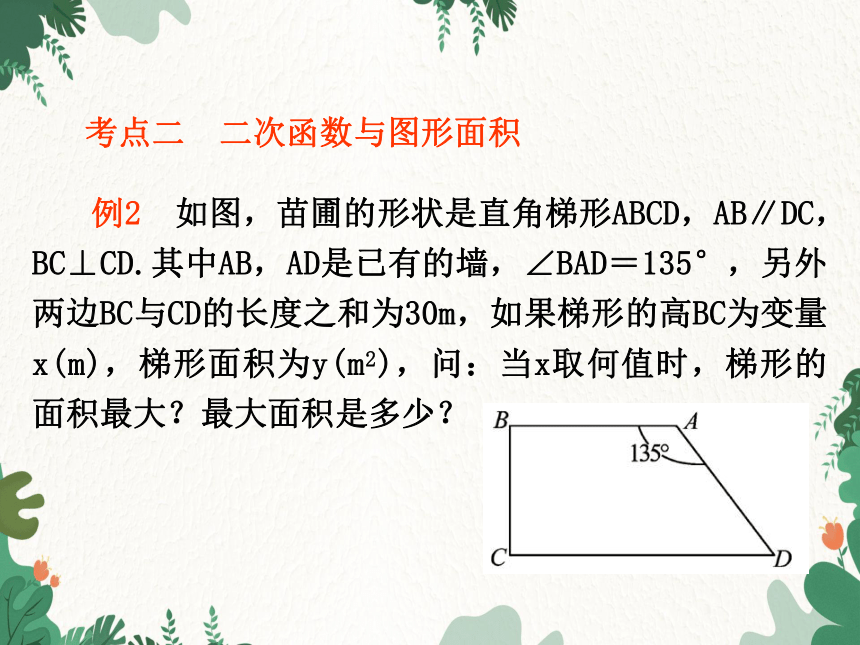
考点二 二次函数与图形面积
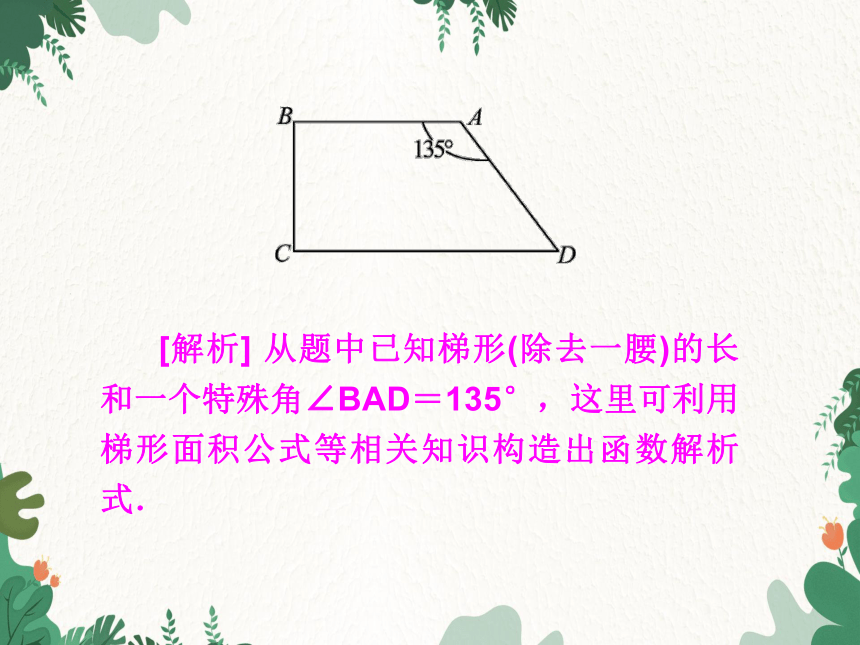
例2 如图,苗圃的形状是直角梯形ABCD,AB∥DC,BC⊥CD.其中AB,AD是已有的墙,∠BAD=135°,另外两边BC与CD的长度之和为30m,如果梯形的高BC为变量x(m),梯形面积为y(m2),问:当x取何值时,梯形的面积最大?最大面积是多少?
[解析] 从题中已知梯形(除去一腰)的长和一个特殊角∠BAD=135°,这里可利用梯形面积公式等相关知识构造出函数解析式.
解:作AE⊥CD于点E,如图,
因为∠BAD=135°,则∠ADC=45°.
∴ BC=AE=ED.
又BC+CE+ED=30,
则AB=30-2x,CD=30-x,故
y=(AB+CD)·BC/2=[(30-2x)+(30-x)]·x/2,
∴ y=-3/2x 2+30x(0<x<15).
配方得:
即当x=10时,y最大=150(米).
考点三 二次函数与生活应用
例3 利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其他费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
“每每型”二次函数模型成为近年考试的热点问题,其特点就是每下降,就每增加;或每增长,就每减少.解决这类问题的关键就是找到单价提高后,该经销店每天售出的建筑材料的吨数,而等量关系为销售利润=销售吨数×每吨的利润.
考点四 二次函数与体育活动
[解析] 解决这个问题的关键是正确地进行数学建模,将运动员在空中的运动路线抽象为所给出的直角坐标系中的抛物线,用待定系数法求出表达式,再利用函数知识求解.
4ac-b2
4a
2
1.通过这节课的学习你有哪些问题?
2.回顾本章知识,你还有哪些问题?
课堂小结
完成本课时的习题。
课后作业
第 二 章 二次函数
九年级数学 下 BS
章末复习
知识结构
1.定义:一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做x的二次函数.
重点解惑
2.填表:
开口向上
开口向上
开口向上
开口向上
开口向上
开口向下
开口向下
开口向下
开口向下
开口向下
y轴
y轴
x=h
x=h
(0,0)
(0,k)
(h,0)
(h,k)
(1)抛物线y=-2x +1的对称轴是 ,顶点坐标是 。
(2)抛物线y=(x-3) -1的最小值是 。
y轴(x=0)
(0,1)
-1
(3)写出一个图象经过原点的二次函数解析式:
。
y=x -2x
(4)抛物线y=-x -2x+3与x轴交于点A( )、
B( ),与y轴交于点C( ),且△ABC的面积为 。
1,0
-3,0
0,3
6
(5)在墙边(足够长)的空地上,准备用36m长的篱笆围一块矩形花圃,问长是多少时,才能使围成的面积最大,最大面积是多少?
解: 设长为xm时 ,面积为y m2
由已知条件得 : y= (36-2x)·x
y= -2(x-9)2+162
∴ 当 x=9 m时, y 的最大面积是162m2
考点一 一元二次方程与二次函数的关系
B
[解析] B 先根据(-7) 2-4k(-7)≥0得到k≥ ,由于是抛物线,所以k≠0.
考点二 二次函数与图形面积
例2 如图,苗圃的形状是直角梯形ABCD,AB∥DC,BC⊥CD.其中AB,AD是已有的墙,∠BAD=135°,另外两边BC与CD的长度之和为30m,如果梯形的高BC为变量x(m),梯形面积为y(m2),问:当x取何值时,梯形的面积最大?最大面积是多少?
[解析] 从题中已知梯形(除去一腰)的长和一个特殊角∠BAD=135°,这里可利用梯形面积公式等相关知识构造出函数解析式.
解:作AE⊥CD于点E,如图,
因为∠BAD=135°,则∠ADC=45°.
∴ BC=AE=ED.
又BC+CE+ED=30,
则AB=30-2x,CD=30-x,故
y=(AB+CD)·BC/2=[(30-2x)+(30-x)]·x/2,
∴ y=-3/2x 2+30x(0<x<15).
配方得:
即当x=10时,y最大=150(米).
考点三 二次函数与生活应用
例3 利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其他费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
“每每型”二次函数模型成为近年考试的热点问题,其特点就是每下降,就每增加;或每增长,就每减少.解决这类问题的关键就是找到单价提高后,该经销店每天售出的建筑材料的吨数,而等量关系为销售利润=销售吨数×每吨的利润.
考点四 二次函数与体育活动
[解析] 解决这个问题的关键是正确地进行数学建模,将运动员在空中的运动路线抽象为所给出的直角坐标系中的抛物线,用待定系数法求出表达式,再利用函数知识求解.
4ac-b2
4a
2
1.通过这节课的学习你有哪些问题?
2.回顾本章知识,你还有哪些问题?
课堂小结
完成本课时的习题。
课后作业
