3-7弧长及扇形的面积[下学期]
图片预览






文档简介
课件20张PPT。第三章 圆北师大版九年级下册3.7 弧长及扇形的面积一 复习提问:已知⊙O半径为R,⊙O的周长C是多少? ⊙O的面积S是多少?C=2πR
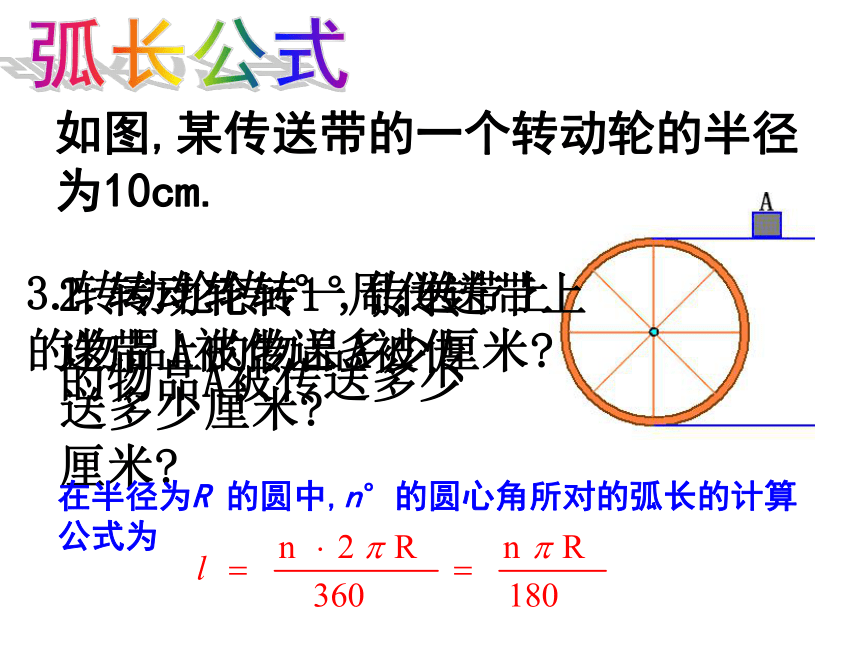
这里π=3.14159…,这个无限不循环的小数叫做圆周率. S=лR2弧长公式如图,某传送带的一个转动轮的半径为10cm.1.转动轮转一周,传送带上的物品A被传送多少厘米?2.转动轮转1°,传送带上
的物品A被传送多少
厘米?3.转动轮转n°,传送带上的物品A被传送多少厘米?在半径为R 的圆中,n°的圆心角所对的弧长的计算公式为注意:(1)在应用弧长公式l 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位
的;
注意:(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只
有在同圆或等圆中,才可能是等弧.
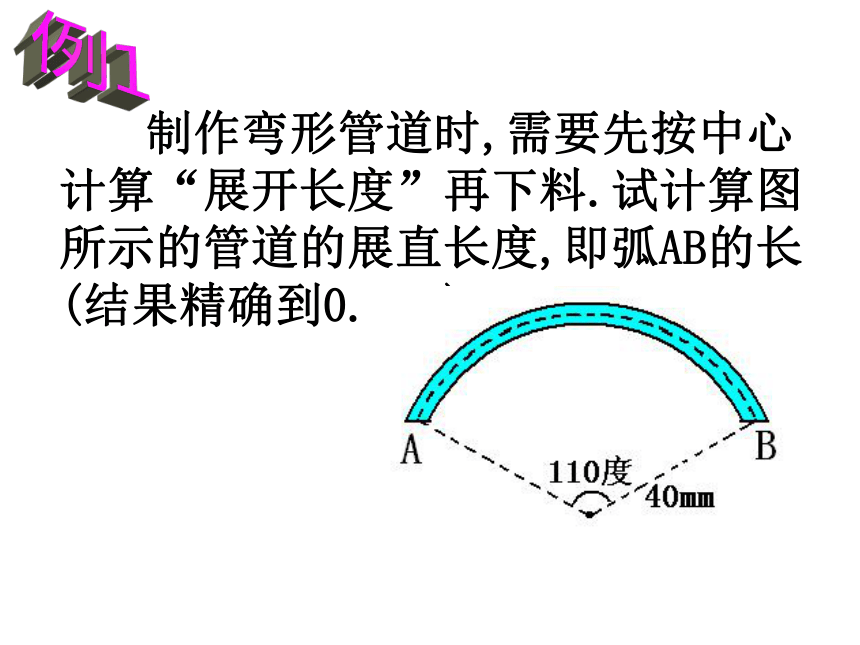
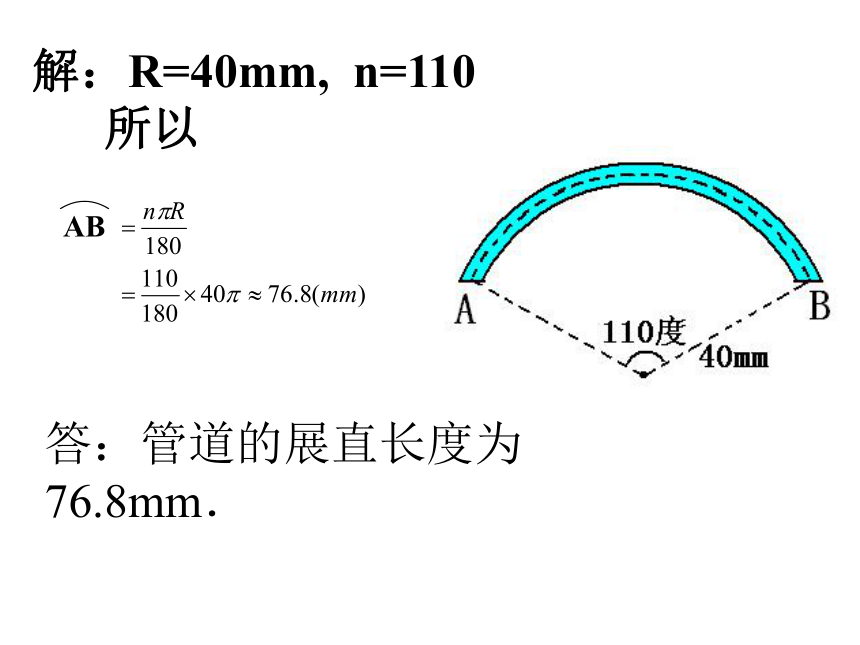
制作弯形管道时,需要先按中心计算“展开长度”再下料.试计算图所示的管道的展直长度,即弧AB的长(结果精确到0.1mm).例1解:R=40mm, n=110
所以
答:管道的展直长度为76.8mm. 想一想 在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的另一端拴着一只狗.(1)这只狗的最大活动区域有多大?(2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大?想一想 在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的另一端拴着一只狗.在半径为R 的圆中,n°的圆心角所对的扇形面积的计算公式为5、已知半径为2的扇形,面积为 ,则这个扇形的弧
长=____. 练习比较弧长公式与扇形面积公式S扇形l 弧在这两个公式中,弧长和扇形面积都和圆心角n°、半径R有关系,因此l 和S之间也有一定的关系,你能猜得出吗? 如图,扇形AOB的半径为12cm, ∠AOB=120°,求:
(1)AB的长(结果精确到0.1cm) 例2(2)扇形AOB的面积(结果精确到0.1cm2)1、已知扇形的圆心角为120°,半径为
2,则这个扇形的面积,S扇=_ .练习2、已知扇形面积为 ,圆心角为120°,则这个扇形的半径R=____. 24、已知半径为2cm的扇形,其弧长为 ,则这个扇形的面积,
S扇=_.
练习3、已知半径为2的扇形,面积为 ,则它的圆心角的度数=____. 120°6、扇形AOB的半径为12cm,∠AOB=120°,求 的长(结果精确到0.1cm)和扇形AOB的面积(结果精确到0.1cm2)练习1、如图,水平放置的一个油管的横截面半径为12cm,其中有油的部分油面高6cm,求截面上有油部分的面积(结果精确到0.1cm2).随堂练习若求由优弧ACB和弦AB组成的阴影部分的面积,则如图,两个同心圆被两条半径截得的AB的长为6,CD的长为10,AC=12,求阴影(红色)部分ABDC的面积. 拓展思考OBDAC例1、已知:如图,圆环的外圆周长C1=250cm,内圆周
长C2=150cm,求圆环的宽度d (精确到1mm).
解:设外圆的半径为R1,内圆的半径为R2,则
d= . ∵ , ,
∴ (cm) 3.探索弧长及扇形的面积之间的关系,并能已知l、n、R、S中的两个量求另一两个量. 1.探索弧长的计算公式 ,并运用公式进行计算. 2.探索扇形的面积公式 ,并运用公式进行计算. 课堂小结
这里π=3.14159…,这个无限不循环的小数叫做圆周率. S=лR2弧长公式如图,某传送带的一个转动轮的半径为10cm.1.转动轮转一周,传送带上的物品A被传送多少厘米?2.转动轮转1°,传送带上
的物品A被传送多少
厘米?3.转动轮转n°,传送带上的物品A被传送多少厘米?在半径为R 的圆中,n°的圆心角所对的弧长的计算公式为注意:(1)在应用弧长公式l 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位
的;
注意:(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只
有在同圆或等圆中,才可能是等弧.
制作弯形管道时,需要先按中心计算“展开长度”再下料.试计算图所示的管道的展直长度,即弧AB的长(结果精确到0.1mm).例1解:R=40mm, n=110
所以
答:管道的展直长度为76.8mm. 想一想 在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的另一端拴着一只狗.(1)这只狗的最大活动区域有多大?(2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大?想一想 在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的另一端拴着一只狗.在半径为R 的圆中,n°的圆心角所对的扇形面积的计算公式为5、已知半径为2的扇形,面积为 ,则这个扇形的弧
长=____. 练习比较弧长公式与扇形面积公式S扇形l 弧在这两个公式中,弧长和扇形面积都和圆心角n°、半径R有关系,因此l 和S之间也有一定的关系,你能猜得出吗? 如图,扇形AOB的半径为12cm, ∠AOB=120°,求:
(1)AB的长(结果精确到0.1cm) 例2(2)扇形AOB的面积(结果精确到0.1cm2)1、已知扇形的圆心角为120°,半径为
2,则这个扇形的面积,S扇=_ .练习2、已知扇形面积为 ,圆心角为120°,则这个扇形的半径R=____. 24、已知半径为2cm的扇形,其弧长为 ,则这个扇形的面积,
S扇=_.
练习3、已知半径为2的扇形,面积为 ,则它的圆心角的度数=____. 120°6、扇形AOB的半径为12cm,∠AOB=120°,求 的长(结果精确到0.1cm)和扇形AOB的面积(结果精确到0.1cm2)练习1、如图,水平放置的一个油管的横截面半径为12cm,其中有油的部分油面高6cm,求截面上有油部分的面积(结果精确到0.1cm2).随堂练习若求由优弧ACB和弦AB组成的阴影部分的面积,则如图,两个同心圆被两条半径截得的AB的长为6,CD的长为10,AC=12,求阴影(红色)部分ABDC的面积. 拓展思考OBDAC例1、已知:如图,圆环的外圆周长C1=250cm,内圆周
长C2=150cm,求圆环的宽度d (精确到1mm).
解:设外圆的半径为R1,内圆的半径为R2,则
d= . ∵ , ,
∴ (cm) 3.探索弧长及扇形的面积之间的关系,并能已知l、n、R、S中的两个量求另一两个量. 1.探索弧长的计算公式 ,并运用公式进行计算. 2.探索扇形的面积公式 ,并运用公式进行计算. 课堂小结
