北师大版九年级下册第三章 圆复习课件(共19张PPT)
文档属性
| 名称 | 北师大版九年级下册第三章 圆复习课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 21:45:30 | ||
图片预览





文档简介
(共19张PPT)
第 三 章 圆
九年级数学 下 BS
章末复习
《圆》知识点
点的轨迹
三种位置关系
垂径定理
圆心角定理
圆周角定理
圆的内接四边形定理
切线的性质与判定定理、切线长定理
圆内接正多边形
扇形弧长、面积公式
知识回顾
点的轨迹
圆:
圆的外部:
圆的内部:
集合:
圆可以看作是到定点的距离等于定长的点的集合;
可以看作是到定点的距离大于定长的点的集合;
可以看作是到定点的距离小于定长的点的集合.
1、到定点的距离等于定长的点的轨迹是:以定点为圆心,定长为半径的圆;
2、到线段两端点距离相等的点的轨迹是:线段的中垂线;
3、到角两边距离相等的点的轨迹是:角的平分线;
4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;
5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线.
轨迹:
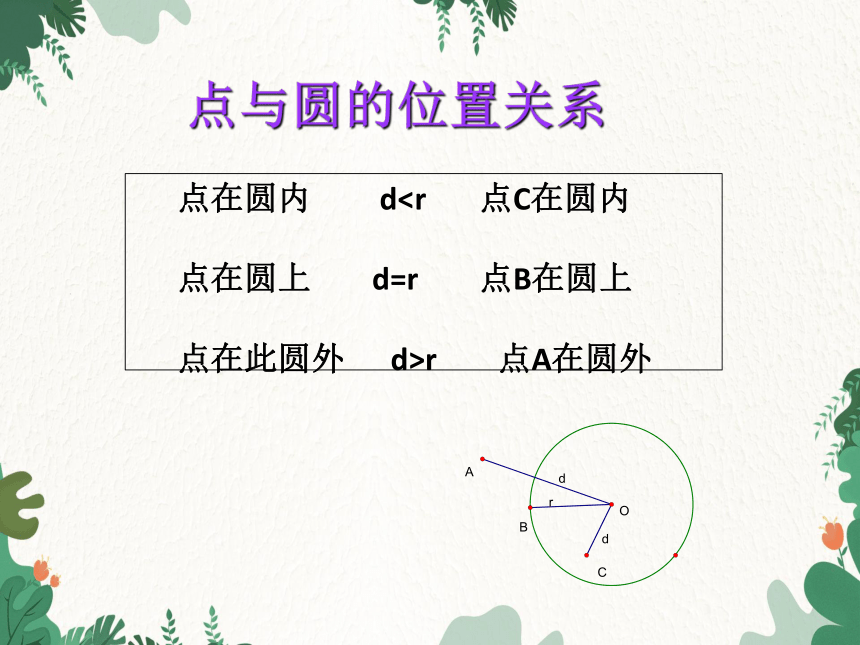
点与圆的位置关系
点在圆内 d点在圆上 d=r 点B在圆上
点在此圆外 d>r 点A在圆外
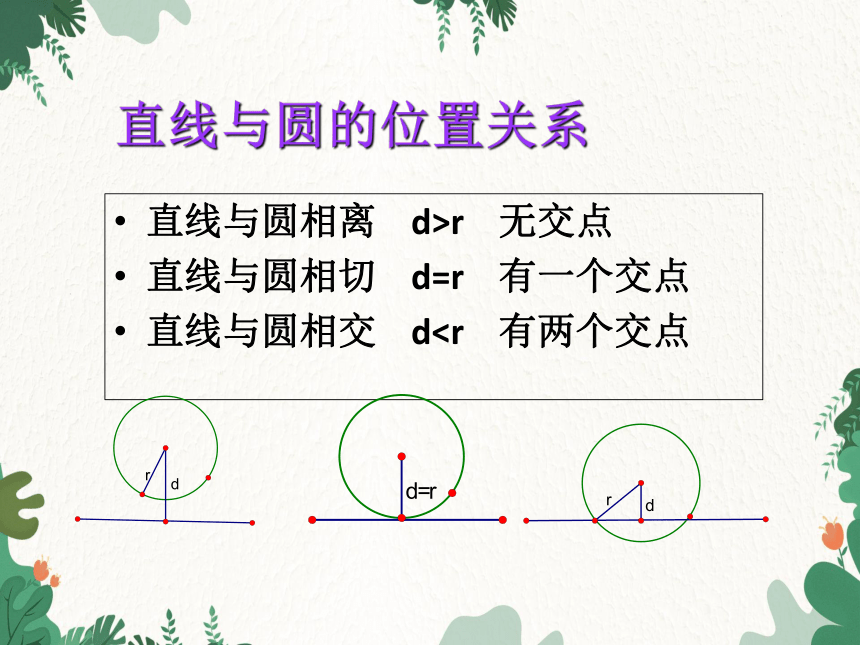
直线与圆的位置关系
直线与圆相离 d>r 无交点
直线与圆相切 d=r 有一个交点
直线与圆相交 d垂径定理
垂径定理:垂直于弦的直径平分弦且平分弦所对的弧
推论1:
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其他3个结论,即:
①AB是直径 ②AB⊥CD ③CE=DE ④ ⑤
①② ③④⑤或①③ ②④⑤或……
推论2:圆的两条平行弦所夹的弧相等。
即:在⊙O中,∵AB∥CD
∴
O
E
D
C
B
A
圆心角定理
圆心角定理:同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等,弦心距相等
此定理也称1推3定理,即上述四个结论中,只要知道其中的1个相等,则可以推出其它的3个结论
也即:①∠AOB=∠DOE ②AB=DE ③OC=OF ④
① ②③④或② ①③④……
圆周角定理
圆周角定理:同一条弧所对的圆周角等于它所对的圆心角的一半
即:∵∠AOB和∠ACB是 所对的圆心角和圆周角
∴
圆周角定理的推论:
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧
即:在⊙O中,∵∠C、∠D都是 所对的圆周角
∴∠C=∠D
推论2:半圆或直径所对的圆周角是直角;圆周角是直角所对的弧是半圆,所对的弦是直径
即:在⊙O中,
∵AB是直径 ∴∠C=90°
或∵∠C=90°
∴AB是直径
推论3:三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形
即:在△ABC中,∵OC=OA=OB
∴△ABC是直角三角形或∠C=90°
注:此推论实是初二年级几何中矩形的推论:在直角三角形中斜边上的中线等于斜边的一半的逆定理。
弦切角定理
弦切角定理:弦切角等于所夹弧所对的圆周角
即:∵MN是切线,AB是弦
∴∠BAM=∠BCA
推论:如果两个弦切角所夹的弧相等,那么这两个弦切角也相等。
圆内接四边形
圆的内接四边形定理:圆的内接四边形的对角互补,外角等于它的内对角。
即:在⊙O中,
∵四边形ABCD是内接四边形
∴∠C+∠BAD=180°
∠B+∠D=180°
∠DAE=∠C
切线的性质与判定定理
(1)性质定理:切线垂直于过切点的半径(如上图)
推论1:过圆心垂直于切线的直线必过切点
推论2:过切点垂直于切线的直线必过圆心
以上三个定理及推论也称二推一定理:
即:过圆心 过切点 垂直切线中知道其中两个条件推出最后一个条件
∵MN是切线
∴MN⊥OA
2)判定定理:过半径外端且垂直于半径的直线是切线
两个条件:过半径外端且垂直半径,二者缺一不可
即:∵MN⊥OA且MN过半径OA外端
∴MN是⊙O的切线
切线长定理
切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角。
即:∵PA、PB是圆的两条切线
∴PA=PB
PO平分∠BPA
圆内接正多边形的计算
(1)正三角形
在⊙O中 △ABC是正三角形,有关计算在Rt△BOD中进行,OD:BD:OB=
(2)正四边形
同理,四边形的有关计算在Rt△OAE中进行,OE :AE:OA=
(3)正六边形
同理,六边形的有关计算在Rt△OAB中进行,AB:OB:OA=
弧长、扇形面积公式
(1)弧长公式:
(2)扇形面积公式:
完成本课时的习题.
课后作业
第 三 章 圆
九年级数学 下 BS
章末复习
《圆》知识点
点的轨迹
三种位置关系
垂径定理
圆心角定理
圆周角定理
圆的内接四边形定理
切线的性质与判定定理、切线长定理
圆内接正多边形
扇形弧长、面积公式
知识回顾
点的轨迹
圆:
圆的外部:
圆的内部:
集合:
圆可以看作是到定点的距离等于定长的点的集合;
可以看作是到定点的距离大于定长的点的集合;
可以看作是到定点的距离小于定长的点的集合.
1、到定点的距离等于定长的点的轨迹是:以定点为圆心,定长为半径的圆;
2、到线段两端点距离相等的点的轨迹是:线段的中垂线;
3、到角两边距离相等的点的轨迹是:角的平分线;
4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;
5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线.
轨迹:
点与圆的位置关系
点在圆内 d
点在此圆外 d>r 点A在圆外
直线与圆的位置关系
直线与圆相离 d>r 无交点
直线与圆相切 d=r 有一个交点
直线与圆相交 d
垂径定理:垂直于弦的直径平分弦且平分弦所对的弧
推论1:
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其他3个结论,即:
①AB是直径 ②AB⊥CD ③CE=DE ④ ⑤
①② ③④⑤或①③ ②④⑤或……
推论2:圆的两条平行弦所夹的弧相等。
即:在⊙O中,∵AB∥CD
∴
O
E
D
C
B
A
圆心角定理
圆心角定理:同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等,弦心距相等
此定理也称1推3定理,即上述四个结论中,只要知道其中的1个相等,则可以推出其它的3个结论
也即:①∠AOB=∠DOE ②AB=DE ③OC=OF ④
① ②③④或② ①③④……
圆周角定理
圆周角定理:同一条弧所对的圆周角等于它所对的圆心角的一半
即:∵∠AOB和∠ACB是 所对的圆心角和圆周角
∴
圆周角定理的推论:
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧
即:在⊙O中,∵∠C、∠D都是 所对的圆周角
∴∠C=∠D
推论2:半圆或直径所对的圆周角是直角;圆周角是直角所对的弧是半圆,所对的弦是直径
即:在⊙O中,
∵AB是直径 ∴∠C=90°
或∵∠C=90°
∴AB是直径
推论3:三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形
即:在△ABC中,∵OC=OA=OB
∴△ABC是直角三角形或∠C=90°
注:此推论实是初二年级几何中矩形的推论:在直角三角形中斜边上的中线等于斜边的一半的逆定理。
弦切角定理
弦切角定理:弦切角等于所夹弧所对的圆周角
即:∵MN是切线,AB是弦
∴∠BAM=∠BCA
推论:如果两个弦切角所夹的弧相等,那么这两个弦切角也相等。
圆内接四边形
圆的内接四边形定理:圆的内接四边形的对角互补,外角等于它的内对角。
即:在⊙O中,
∵四边形ABCD是内接四边形
∴∠C+∠BAD=180°
∠B+∠D=180°
∠DAE=∠C
切线的性质与判定定理
(1)性质定理:切线垂直于过切点的半径(如上图)
推论1:过圆心垂直于切线的直线必过切点
推论2:过切点垂直于切线的直线必过圆心
以上三个定理及推论也称二推一定理:
即:过圆心 过切点 垂直切线中知道其中两个条件推出最后一个条件
∵MN是切线
∴MN⊥OA
2)判定定理:过半径外端且垂直于半径的直线是切线
两个条件:过半径外端且垂直半径,二者缺一不可
即:∵MN⊥OA且MN过半径OA外端
∴MN是⊙O的切线
切线长定理
切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角。
即:∵PA、PB是圆的两条切线
∴PA=PB
PO平分∠BPA
圆内接正多边形的计算
(1)正三角形
在⊙O中 △ABC是正三角形,有关计算在Rt△BOD中进行,OD:BD:OB=
(2)正四边形
同理,四边形的有关计算在Rt△OAE中进行,OE :AE:OA=
(3)正六边形
同理,六边形的有关计算在Rt△OAB中进行,AB:OB:OA=
弧长、扇形面积公式
(1)弧长公式:
(2)扇形面积公式:
完成本课时的习题.
课后作业
