2022届高考数学二轮专题微课-椭圆中的蒙日圆课件(20张PPT)
文档属性
| 名称 | 2022届高考数学二轮专题微课-椭圆中的蒙日圆课件(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 800.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-07 21:47:29 | ||
图片预览






文档简介
(共20张PPT)
专
题
课
微
椭圆中的“蒙日圆”
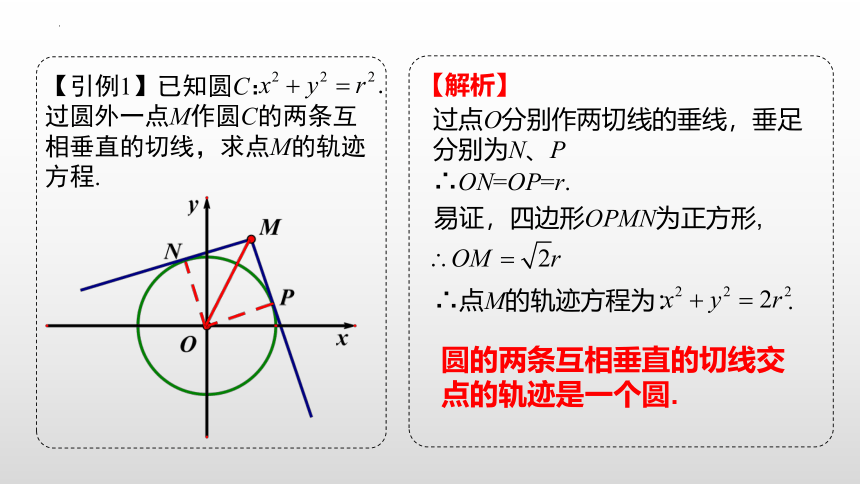
【引例1】已知圆C: 过圆外一点M作圆C的两条互相垂直的切线,求点M的轨迹方程.
【解析】
过点O分别作两切线的垂线,垂足分别为N、P
∴ON=OP=r.
易证,四边形OPMN为正方形,
∴点M的轨迹方程为: .
圆的两条互相垂直的切线交点的轨迹是一个圆.
【引例2】(2014·广东18题)已知椭圆C: ,一个焦点为
,离心率为 .
(1)求椭圆C的标准方程;
(2)若动点P(x0,y0)为椭圆C外一点,且点P到
椭圆C的两条切线相互垂直,求点P的轨迹方程.
P(±3,±2).
【解析】当两条切线中有斜率不存在或斜率为0时,
当两条切线的斜率都存在时,设过P点直线方程为y-y0=k(x-x0).
(9k2+4)x2-18k(kx0-y0)x+9(kx-y0)2-36=0.
∵直线与椭圆相切,
∴△=0
(x02-9)k2-2x0y0k+y02-4=0
∴
综上所述,P的轨迹方程为 .
蒙日圆定理
定理1:椭圆C: 的两条相互垂直的切线的交点P的轨迹方程为 .
蒙日圆
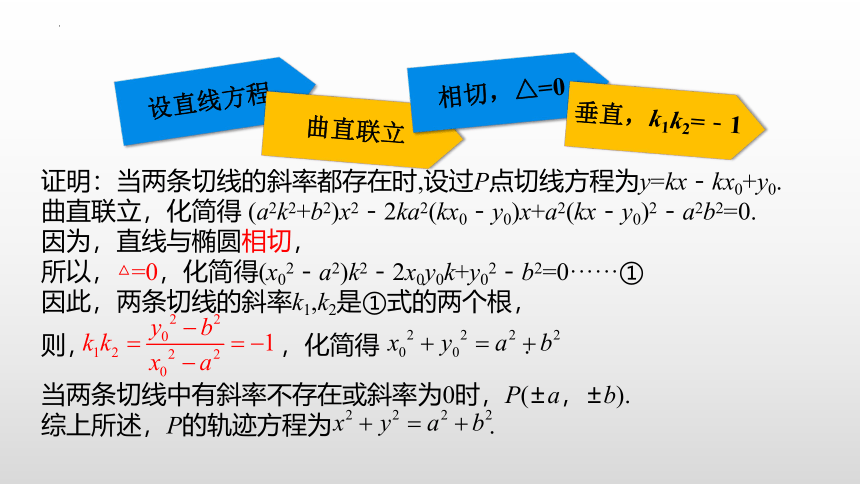
证明:当两条切线的斜率都存在时,设过P点切线方程为y=kx-kx0+y0.
曲直联立,化简得 (a2k2+b2)x2-2ka2(kx0-y0)x+a2(kx-y0)2-a2b2=0.
因为,直线与椭圆相切,
所以,△=0,化简得(x02-a2)k2-2x0y0k+y02-b2=0······①
因此,两条切线的斜率k1,k2是①式的两个根,
则, ,化简得 .
当两条切线中有斜率不存在或斜率为0时,P(±a,±b).
综上所述,P的轨迹方程为 .
设直线方程
曲直联立
相切,△=0
垂直,k1k2=-1
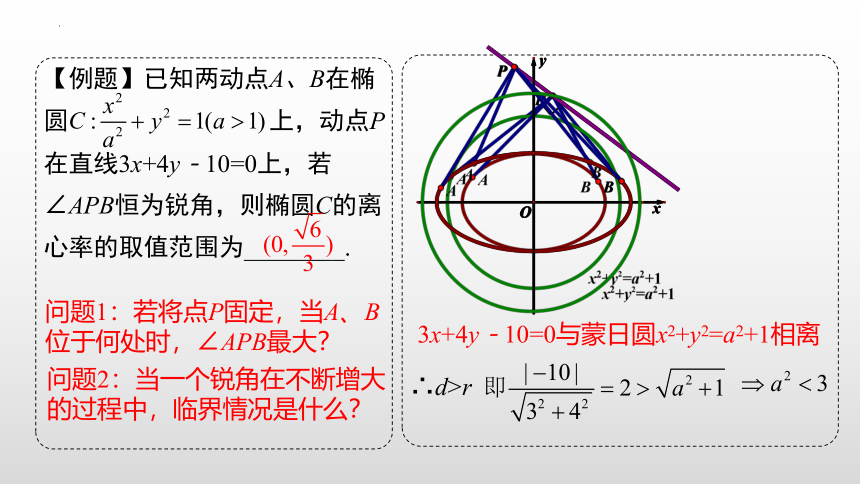
【例题】已知两动点A、B在椭圆 上,动点P在直线3x+4y-10=0上,若∠APB恒为锐角,则椭圆C的离心率的取值范围为________.
3x+4y-10=0与蒙日圆x2+y2=a2+1相离
∴d>r
问题1:若将点P固定,当A、B位于何处时,∠APB最大?
问题2:当一个锐角在不断增大的过程中,临界情况是什么?
蒙日圆定理
定理1:椭圆C: 的两条相互垂直的切线的交点P的轨迹是 .
思考:对于双曲线和抛物线,会有类似结论吗
筷子夹汤圆
圆锥曲线蒙日圆,
切线垂直要齐全。
交点轨迹有两种,
椭双成圆抛准线。
蒙日圆定理应用1
蒙日圆定理应用2
蒙日圆定理应用3
蒙日圆定理应用4
专
题
课
微
椭圆中的“蒙日圆”
【引例1】已知圆C: 过圆外一点M作圆C的两条互相垂直的切线,求点M的轨迹方程.
【解析】
过点O分别作两切线的垂线,垂足分别为N、P
∴ON=OP=r.
易证,四边形OPMN为正方形,
∴点M的轨迹方程为: .
圆的两条互相垂直的切线交点的轨迹是一个圆.
【引例2】(2014·广东18题)已知椭圆C: ,一个焦点为
,离心率为 .
(1)求椭圆C的标准方程;
(2)若动点P(x0,y0)为椭圆C外一点,且点P到
椭圆C的两条切线相互垂直,求点P的轨迹方程.
P(±3,±2).
【解析】当两条切线中有斜率不存在或斜率为0时,
当两条切线的斜率都存在时,设过P点直线方程为y-y0=k(x-x0).
(9k2+4)x2-18k(kx0-y0)x+9(kx-y0)2-36=0.
∵直线与椭圆相切,
∴△=0
(x02-9)k2-2x0y0k+y02-4=0
∴
综上所述,P的轨迹方程为 .
蒙日圆定理
定理1:椭圆C: 的两条相互垂直的切线的交点P的轨迹方程为 .
蒙日圆
证明:当两条切线的斜率都存在时,设过P点切线方程为y=kx-kx0+y0.
曲直联立,化简得 (a2k2+b2)x2-2ka2(kx0-y0)x+a2(kx-y0)2-a2b2=0.
因为,直线与椭圆相切,
所以,△=0,化简得(x02-a2)k2-2x0y0k+y02-b2=0······①
因此,两条切线的斜率k1,k2是①式的两个根,
则, ,化简得 .
当两条切线中有斜率不存在或斜率为0时,P(±a,±b).
综上所述,P的轨迹方程为 .
设直线方程
曲直联立
相切,△=0
垂直,k1k2=-1
【例题】已知两动点A、B在椭圆 上,动点P在直线3x+4y-10=0上,若∠APB恒为锐角,则椭圆C的离心率的取值范围为________.
3x+4y-10=0与蒙日圆x2+y2=a2+1相离
∴d>r
问题1:若将点P固定,当A、B位于何处时,∠APB最大?
问题2:当一个锐角在不断增大的过程中,临界情况是什么?
蒙日圆定理
定理1:椭圆C: 的两条相互垂直的切线的交点P的轨迹是 .
思考:对于双曲线和抛物线,会有类似结论吗
筷子夹汤圆
圆锥曲线蒙日圆,
切线垂直要齐全。
交点轨迹有两种,
椭双成圆抛准线。
蒙日圆定理应用1
蒙日圆定理应用2
蒙日圆定理应用3
蒙日圆定理应用4
同课章节目录
