高中数学北师大版(2019)必修 第一册第四章 对数函数与对数运算:指数函数幂函数对数函数增长的比较提升训练(含解析)
文档属性
| 名称 | 高中数学北师大版(2019)必修 第一册第四章 对数函数与对数运算:指数函数幂函数对数函数增长的比较提升训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 186.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 14:40:24 | ||
图片预览




文档简介
指数函数、幂函数、对数函数增长的比较
基础过关练
题组一 不同增长函数模型的比较
1.下列函数中,增长速度越来越慢的是 ( )
A.y=6x B.y=log6x
C.y=x6 D.y=6x
2.“红豆生南国,春来发几枝.”如图给出了红豆生长时间t(月)与枝数y(枝)的散点图,那么最适合拟合红豆的枝数与生长时间的关系的函数是 ( )
A.指数函数y=2t B.对数函数y=log2t
C.幂函数y=t3 D.二次函数y=2t2
3.三个变量y1,y2,y3,随着变量x的变化情况如下表:
x 1 3 5 7 9 11
y1 5 135 625 1715 3645 6655
y2 5 29 245 2189 19685 177149
y3 5 6.10 6.61 6.95 7.2 7.4
则与x呈对数型函数,指数型函数,幂型函数变化的变量依次为 ( )
A.y1,y2,y3 B.y2,y1,y3
C.y3,y2,y1 D.y1,y3,y2
4.(2020广东惠州高一上期末)有一组实验数据如下表:
t 1.99 3.0 4.0 5.1 6.12
v 1.5 4.04 7.5 12 18.01
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是 ( )
A.v=log2t B.v=lot
C.v= D.v=2t-2
5.函数f(x)=lgx,g(x)=0.3x-1的图像如图所示.
(1)指出图中C1,C2分别对应哪一个函数;
(2)比较两函数的增长差异(以两图像交点为分界点,对f(x),g(x)的大小进行比较).
题组二 不同增长函数模型的应用
6.某林区的森林蓄积量每年比上一年平均增长10.4%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图像大致是 ( )
7.某校甲、乙两食堂某年1月份的营业额相等,甲食堂的营业额逐月增加,并且每月的增加值相同;乙食堂的营业额也逐月增加,且每月增加的百分率相同.已知该年9月份两食堂的营业额又相等,则该年5月份 ( )
A.甲食堂的营业额较高
B.乙食堂的营业额较高
C.甲、乙两食堂的营业额相同
D.不能确定甲、乙哪个食堂的营业额较高
8.一种专门侵占内存的计算机病毒,开机时占据内存2KB,然后每3分钟自身复制一次,复制后所占内存是原来的2倍,那么开机后经过 分钟,该病毒占据64MB内存(1MB=210KB).
9.某人对东北一种松树的生长进行了研究,收集了其高度h(米)与生长时间t(年)的相关数据如下表所示,选择h=mt+b与h=loga(t+1)来拟合h与t的关系,你认为哪个符合 并预测第8年松树的高度.
t(年) 1 2 3 4 5 6
h(米) 0.6 1 1.3 1.5 1.6 1.7
10.某公司承包了一个工程项目,经统计发现该公司在这项工程项目上的月利润P与月份x近似地满足某一函数关系.其中2月到5月所获利润统计如下表:
月份(月) 2 3 4 5
所获利润(亿元) 89 90 89 86
(1)已知该公司的月利润P与月份x近似满足下列中的某一个函数模型:①P(x)=ax2+bx+c;②P(x)=a·bx+c;③P(x)=alogbx+c,请以表中该公司这四个月的利润与月份的数据为依据给出你的选择(需要说明选择该模型的理由),并据此估计该公司8月份在这项工程项目中获得的利润;
(2)根据(1)中选择的函数模型P(x),若该公司承包项目的月成本符合函数模型Q(x)=(单位:亿元),求该公司承包的这项工程项目月成本的最大值及相应的月份.
题组三 不同增长函数模型的图像特征
11.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间后,为了赶时间加快速度行驶.与以上事件吻合得最好的图像是 ( )
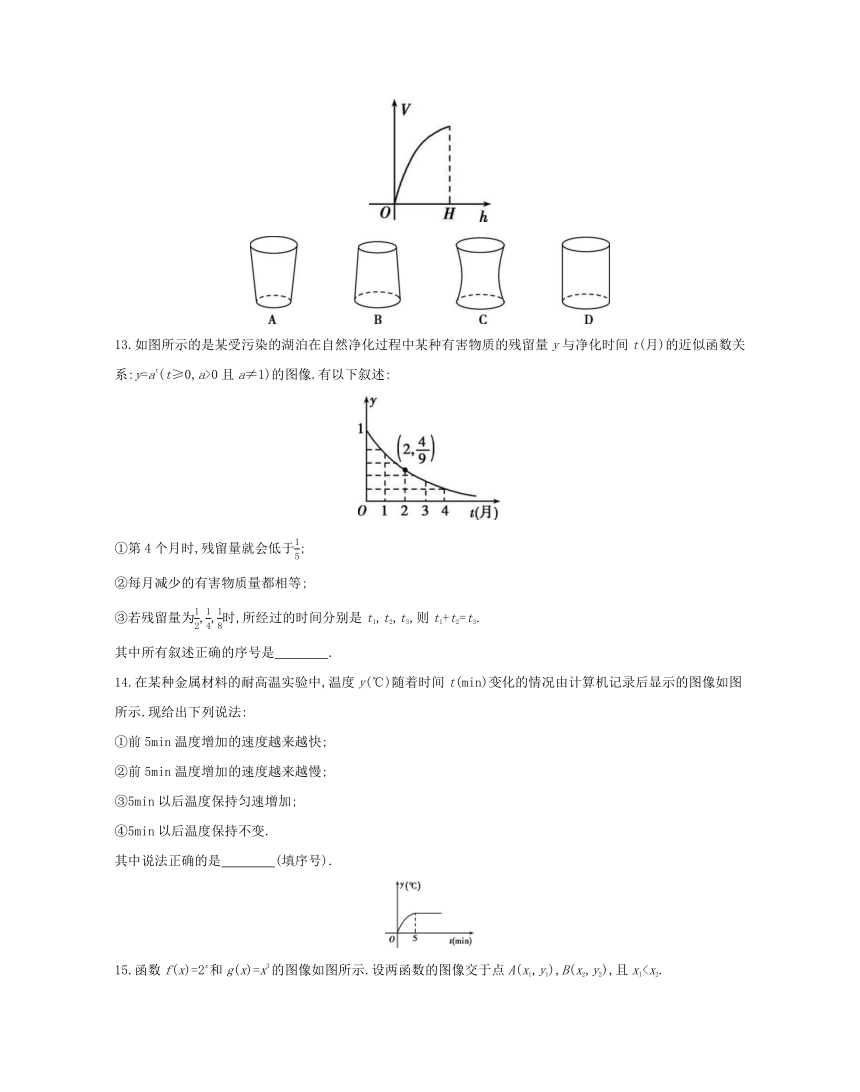
12.向高为H的水瓶内注水,一直到注满为止,如果注水量V与水深h的函数图像如图所示,那么水瓶的形状大致是 ( )
13.如图所示的是某受污染的湖泊在自然净化过程中某种有害物质的残留量y与净化时间t(月)的近似函数关系:y=at(t≥0,a>0且a≠1)的图像.有以下叙述:
①第4个月时,残留量就会低于;
②每月减少的有害物质量都相等;
③若残留量为,,时,所经过的时间分别是t1,t2,t3,则t1+t2=t3.
其中所有叙述正确的序号是 .
14.在某种金属材料的耐高温实验中,温度y(℃)随着时间t(min)变化的情况由计算机记录后显示的图像如图所示.现给出下列说法:
①前5min温度增加的速度越来越快;
②前5min温度增加的速度越来越慢;
③5min以后温度保持匀速增加;
④5min以后温度保持不变.
其中说法正确的是 (填序号).
15.函数f(x)=2x和g(x)=x3的图像如图所示.设两函数的图像交于点A(x1,y1),B(x2,y2),且x1(1)请指出图中曲线C1,C2分别对应的函数;
(2)结合函数图像,比较f(6),g(6),f(2017),g(2017)的大小.
能力提升练
一、选择题
1.已知函数y1=2x,y2=x2,y3=log2x,在区间(0,+∞)上一定存在x0,当x>x0时 ( )
A.2x>x2>log2x B.x2>2x>log2x
C.log2x>2x>x2 D.log2x>x2>2x
2.下表是函数值y随自变量x变化的一组数据,由此判断它最可能的函数模型是 ( )
x 4 5 6
y 15 20 15
A.一次函数模型 B.二次函数模型
C.指数函数模型 D.对数函数模型
3.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:万元)对年销售量y(单位:t)的影响,对近6年的年宣传费xi(i=1,2,…,6)和年销售量yi进行整理,得到的数据如下表所示:
x 1.00 2.00 3.00 4.00 5.00 6.00
y 1.65 2.20 2.60 2.76 2.90 3.10
根据上表数据,下列函数中适宜作为年销售量y关于年宣传费x的拟合函数的是 ( )
A.y=0.5(x+1) B.y=log3x+1.5
C.y=2x-1 D.y=2
4.(2021四川江油一中高一上期中)一种放射性元素最初的质量为500g,按每年10%衰减,则这种放射性元素的半衰期约为 年.(注:剩余质量为最初质量的一半,所需的时间叫作半衰期)(结果精确到0.1,参考数据:lg2=0.3010,lg3=0.4771) ( )
A.5.2 B.6.6 C.7.1 D.8.3
5.(2021湖北武汉三中高一上月考)如图所示,液体从一个圆锥形漏斗漏入一个圆柱形桶中,开始时漏斗中盛满液体,经过3秒漏完,圆柱形桶中液面上升速度是一个常量,则漏斗中液面下降的高度H与下降时间t之间的函数关系的图像只可能是 ( )
6.某小型贸易公司为了实现年终10万元利润的目标,特制订了一个销售人员年终绩效奖励方案:当销售利润为x万元(4≤x≤10)时,奖金y(万元)随销售利润x(万元)的增加而增加,但奖金总数不超过2万元,同时不超过销售利润的,则下列函数中,符合该公司奖励方案的函数模型是(参考数据:lg2≈0.3,lg3≈0.48,lg5≈0.7) ( )
A.y=0.4x B.y=lgx+1
C.y= D.y=1.125x
二、填空题
7.(2020四川泸州泸县一中高一下月考)把物体放在空气中冷却,如果物体原来的温度是θ1℃,空气温度是θ0℃,t分钟后温度θ℃可由公式:θ=θ0+(θ1-θ0)·求得,现有60℃的物体放在15℃的空气中冷却,当物体温度降为35℃时,所用冷却时间t= 分钟.
8.(2020广东深圳中学高一上期中)小菲在选修课中了解到艾宾浩斯记忆曲线,为了解自己记忆一组单词的情况,她记录了随后一个月的有关数据,绘制图像,拟合了记忆保持量 y与时间x(天)之间的函数关系:y=
某同学根据小菲拟合后的信息得到以下结论:
①随着时间的增加,小菲的单词记忆保持量降低;
②9天后,小菲的单词记忆保持量低于40%;
③26天后,小菲的单词记忆保持量不足20%.
其中正确的结论序号有 .
三、解答题
9.(2020江西信丰中学高一上期末)某纪念章于2021年元旦开始上市.通过市场调查,得到该纪念章每一枚的市场价y(单位:元)与上市时间x(单位:天)的数据如下表:
上市时间x天 4 10 36
市场价y元 90 51 90
(1)根据上表数据,从下列函数中选择一个恰当的函数模型描述该纪念章的市场价y与上市时间x的关系,并说明理由;
①y=ax+b(a≠0);②y=ax2+bx+c(a≠0);③y=alogbx(b>0,且b≠1).
(2)利用选取的函数,求该纪念章市场价最低时的上市时间及最低的价格.
10.某医药研究所研发的一种新药,成年人按规定的剂量服用后,据监测:服药后每毫升血液中的含药量y(单位:微克)与时间t(单位:小时)之间近似满足如图所示的曲线对应的函数.
(1)写出服药后y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫升血液中含药量不少于1微克时,治疗有效.问:服药多少小时后开始有治疗效果 治疗效果能持续多少小时 (结果精确到0.1,参考数据:lg2≈0.301)
11.攀枝花是一座资源富集的城市,矿产资源储量巨大,已发现矿种76种,探明储量39种,其中钒、钛资源储量分别占全国的63%和93%,占全球的11%和35%,因此其素有“钒钛之都”的美称.攀枝花市某科研单位在研发钛合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值y(y值越大产品的性能越好)与这种新合金材料的含量x(单位:克)的关系为:当0≤x<7时,y是x的二次函数;当x≥7时,y=.测得部分数据如下表:
x(单位:克) 0 2 6 10 …
y -4 8 8 …
(1)求y关于x的函数关系式y=f(x);
(2)求该新合金材料的含量x为何值时产品的性能达到最佳.
12.()某服装批发市场销售季节性流行服装F,当季节即将来临时,价格呈上升趋势,开始时每件定价为120元,并且每周(7天)每件涨价10元(第1周每件定价为120元,第2周每件定价为130元),4周后开始保持每件160元的价格销售;8周后当季节即将过去时,平均每周每件降价10元,直到第12周末,该服装不再销售.
(1)试建立每件售价A与周次t之间的函数关系式;
(2)若此服装每件进价B与周次t之间的关系式为B=问该服装在第几周每件销售利润R最大 并求出最大值.(注:每件销售利润=售价-进价)
参考答案:
基础过关练
1.B 2.A 3.C 4.C 6.D
7.A 11.C 12.B
1.B A、C中函数的增长速度越来越快,D中一次函数的增长速度不变,只有B中对数函数的增长速度越来越慢,符合题意.
2.A 根据已知所给的散点图,观察得到图像在第一象限,且从左到右图像是上升的,并且增长速度越来越快,根据四个选项中函数的增长趋势可得,用指数函数拟合最好,故选A.
3.C 由题表中的数据可以看出,y3增长缓慢,所以是对数型函数;y2增长速度最快,所以是指数型函数;y1的增长速度仅次于y2,是幂型函数.故选C.
4.C 由题表中的数据可知:v随着t的增大而增大,所以B不符合;
对于A,log21.99≈2,log23≈1.6,log24=2,所以A不符合;
对于C,≈1.5,=4,=7.5,≈12.5,≈18.2,所以C符合;
对于D,2×1.99-2=1.98,2×3-2=4,2×4-2=6,2×5.1-2=8.2,2×6.12-2=10.24,D不符合.故选C.
5.解析 (1)由题中的函数图像特征及变化趋势,知曲线C1对应的函数为g(x)=0.3x-1,
曲线C2对应的函数为f(x)=lgx.
(2)当x∈(0,x1)时,g(x)>f(x);当x∈(x1,x2)时,g(x)f(x).
g(x)呈直线增长,函数值变化是均匀的,f(x)随着x的增大而逐渐增大,其函数值变化得越来越慢.
6.D 设该林区的森林原有蓄积量为a,由题意知,ax=a(1+0.104)y,故y=log1.104x(x≥1),∴y=f(x)的图像大致为D中的图像.
7.A 设甲、乙两食堂1月份的营业额均为m,甲食堂的营业额每月增加a(a>0),乙食堂的营业额每月增加的百分率为x,由题意可知,m+8a=m×(1+x)8,则5月份甲食堂的营业额y1=m+4a,乙食堂的营业额y2=m×(1+x)4=.因为-=(m+4a)2-m(m+8a)=16a2>0,所以y1>y2,故该年5月份甲食堂的营业额较高.
8.答案 45
解析 设开机后经过n个3分钟,该病毒占据64MB内存,
则2×2n=64×210=216,解得n=15,故时间为15×3=45(分钟).
9.解析 根据题表中数据作出散点图如图.
由图像可以看出增长的速度越来越慢,用一次函数模型拟合不合适,选用对数函数模型比较合理.
不妨将(2,1)代入h=loga(t+1)中,得1=loga3,解得a=3.
故可用函数h=log3(t+1)来拟合这个实际问题.
当t=8时,求得h=log3(8+1)=2(米),
故可预测第8年松树的高度为2米.
10.解析 (1)易知a≠0,因为P(x)=a·bx+c,P(x)=alogbx+c为单调函数,由所给数据知,满足条件的函数不单调,所以选取P(x)=ax2+bx+c进行描述.
将题表中(2,89),(3,90),(4,89)代入P(x),得到解方程组得所以该公司月利润P与月份x近似满足的函数为P(x)=-x2+6x+81,x∈[1,12],x∈N+,
当x=8时,得P=65(亿元).
所以8月份所获得的利润约为65亿元.
(2)由(1)得,Q(x)=
=.当x=2时,Q(x)max=11.
所以该公司承包的这项工程项目月成本的最大值为11亿元,相应的月份为2月.
11.C 开始时小明匀速行驶,所得图像为一条直线,且距离学校越来越近,故排除A.因交通堵塞停留了一段时间,与学校的距离不变,故排除D.后来为了赶时间加快速度行驶,故排除B.故选C.
12.B 水深h为自变量,随着h的增大,A中V的增长速度越来越快,C中先慢后快再慢,D中增长速度不变,只有B中V的增长速度越来越慢.故选B.
13.答案 ①③
解析 根据题意,函数的图像经过点2,,故函数为y=.易知①③正确.
14.答案 ②④
解析 因为温度y关于时间t的图像是先凸后平,所以前5min每当t增加一个单位时,相应的增量Δy越来越小,而5min后y关于t的增量保持为0,所以②④正确.
15.解析 (1)曲线C1对应的函数为g(x)=x3,曲线C2对应的函数为f(x)=2x.
(2)∵f(1)=2>g(1)=1,f(2)=4g(10)=1000,∴1由题图可以看出,当x1f(x)当x>x2时,f(x)>g(x),
∴f(2017)>g(2017).
又g(2017)>g(6),
∴f(2017)>g(2017)>g(6)>f(6).
能力提升练
1.A 2.B 3.B 4.B 5.B
6.B
一、选择题
1.A 由于指数函数增长最快,对数函数增长最慢,因此当x很大时,指数函数值最大,对数函数值最小,即在区间(0,+∞)上一定存在x0,当x>x0时,2x>x2>log2x,故选A.
2.B 当自变量x由4增大到5时,函数值y由15增大到20;当自变量x由5增大到6时,函数值y由20减小到15.因此函数不是单调函数,从而函数模型不可能是一次函数模型、指数函数模型和对数函数模型,故选B.
3.B 由题表知,当自变量增加1个单位时,函数值依次增加0.55、0.40、0.16、0.14、0.20,因此A、C不符合题意;当x取1、4时,y=2的值分别为2、4,与题表中的数据相差较大,故选B.
4.B 设这种放射性元素的半衰期为x年,则500(1-10%)x=250,
所以(1-10%)x=,所以log0.9=x,
所以x=lo2,
所以x=,
所以x=,
所以x=≈6.6.
故选B.
解题模板
求解和对数有关的实际问题的思路:
(1)根据题设条件列出符合的关于待求量的等式;
(2)利用指对互化、对数运算法则以及对数运算性质、对数换底公式求出待求量的值.
5.B 由于所给的圆锥形漏斗上口大于下口,
当时间取t时,漏斗中液面下落的高度不
会达到漏斗高度的,对比四个选项的图像可得结果.
故选B.
6.B A选项中,当x=10时,y=4,超过2万元,故A不符合;B选项中,y=lgx+1在[4,10]上是增函数,x=10时,ymax=2,结合图像(如图)知:lgx+1<在x∈[4,10]上恒成立,故B符合;
C选项中,当x=10时,y=>2,超过2万元,故C不符合;
D选项中,当x=10时,y=,设=a,则lga=10(lg9-lg8)≈0.6,
因此a≈100.6>>2,超过2万元,故D不符合.故选B.
二、填空题
7.答案 2
解析 由题意,得θ0=15℃,θ1=60℃,θ=35℃,
∵θ=θ0+(θ1-θ0)·,
∴35=15+(60-15)·,
∴====,
解得t=2.
8.答案 ①②
解析 由y=
可得y随着x的增加而减少,故①正确;
当1,故9天后,小菲的单词记忆保持量低于40%,26天后,小菲的单词记忆保持量高于20%,故②正确,③错误.故答案为①②.
三、解答题
9.信息提取 ①当x=4,10,36时,y依次为90,51,90;②给出三个函数模型,选择一个恰当的函数模型描述该纪念章的市场价y与上市时间x的关系.
数学建模 本题以经济生活中纪念章的市场价的估算为背景,建立函数模型,通过比较函数值增长的快慢选择最恰当的函数模型进行估算.求解时,首先确定三种模型的解析式,分析、验证函数模型,找出最接近的函数模型.
解析 (1)∵随着时间x的增加,y的值先减后增,
而所给的三个函数中,y=ax+b(a≠0)和y=alogbx(b>0,且b≠1)显然都是单调函数,不满足题意,
∴选取y=ax2+bx+c(a≠0).
(2)由题知,把点(4,90),(10,51),(36,90)代入y=ax2+bx+c中,
得解得a=,b=-10,c=126,
∴y=x2-10x+126=(x-20)2+26,
∴当x=20时,ymin=26.
故该纪念章市场价最低时的上市时间为20天,最低的价格为26元.
10.解析 (1)根据题中图像知:当0≤t<1时,y=4t;
当t≥1时,y=a·0.8t,由t=1时,y=4得4=a·0.8,所以a=5,即y=5×0.8t.
因此y=
(2)根据题意,由4t≥1(0≤t<1),解得0.25≤t<1;由5×0.8t≥1(t≥1),得0.8t≥0.2,
所以1≤t≤==≈7.21,
所以0.25≤t≤7.21,
又7.21-0.25=6.96≈7.0,
所以服药0.25小时(即15分钟)后开始有治疗效果,治疗效果能持续7.0小时.
11.解析 (1)当0≤x<7时,y是x的二次函数,可设y=ax2+bx+c(a≠0),
由x=0,y=-4可得c=-4,
由x=2,y=8,可得4a+2b=12,
由x=6,y=8,可得36a+6b=12,
解得a=-1,b=8,即有y=-x2+8x-4;
当x≥7时,y=,由x=10,y=,可得m=8,即有y=.
综上可得,y=
(2)当0≤x<7时,y=-x2+8x-4=-(x-4)2+12,
所以当x=4时,y取得最大值12;
当x≥7时,y=递减,可得y≤3,
所以当x=7时,y取得最大值3.
综上可得,当x=4时产品的性能达到最佳.
12.解析 (1)根据题意计算得:
当t∈(0,4]且t∈N+时,A=110+10t;当t∈(4,8]且t∈N+时,A=160;
当t∈(8,12]且t∈N+时,A=240-10t.
故A=
(2)因为每件销售利润=售价-进价,所以R=A-B,
当t∈(0,4]且t∈N+时,R=4t+30,
t=4时,Rmax=46;
当t∈(4,8]且t∈N+时,R=56;
当t∈(8,12]且t∈N+时,R=136-10t,t=9时,Rmax=46.
故该服装在第5,6,7,8周每件销售利润R最大,最大值是56元.
基础过关练
题组一 不同增长函数模型的比较
1.下列函数中,增长速度越来越慢的是 ( )
A.y=6x B.y=log6x
C.y=x6 D.y=6x
2.“红豆生南国,春来发几枝.”如图给出了红豆生长时间t(月)与枝数y(枝)的散点图,那么最适合拟合红豆的枝数与生长时间的关系的函数是 ( )
A.指数函数y=2t B.对数函数y=log2t
C.幂函数y=t3 D.二次函数y=2t2
3.三个变量y1,y2,y3,随着变量x的变化情况如下表:
x 1 3 5 7 9 11
y1 5 135 625 1715 3645 6655
y2 5 29 245 2189 19685 177149
y3 5 6.10 6.61 6.95 7.2 7.4
则与x呈对数型函数,指数型函数,幂型函数变化的变量依次为 ( )
A.y1,y2,y3 B.y2,y1,y3
C.y3,y2,y1 D.y1,y3,y2
4.(2020广东惠州高一上期末)有一组实验数据如下表:
t 1.99 3.0 4.0 5.1 6.12
v 1.5 4.04 7.5 12 18.01
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是 ( )
A.v=log2t B.v=lot
C.v= D.v=2t-2
5.函数f(x)=lgx,g(x)=0.3x-1的图像如图所示.
(1)指出图中C1,C2分别对应哪一个函数;
(2)比较两函数的增长差异(以两图像交点为分界点,对f(x),g(x)的大小进行比较).
题组二 不同增长函数模型的应用
6.某林区的森林蓄积量每年比上一年平均增长10.4%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图像大致是 ( )
7.某校甲、乙两食堂某年1月份的营业额相等,甲食堂的营业额逐月增加,并且每月的增加值相同;乙食堂的营业额也逐月增加,且每月增加的百分率相同.已知该年9月份两食堂的营业额又相等,则该年5月份 ( )
A.甲食堂的营业额较高
B.乙食堂的营业额较高
C.甲、乙两食堂的营业额相同
D.不能确定甲、乙哪个食堂的营业额较高
8.一种专门侵占内存的计算机病毒,开机时占据内存2KB,然后每3分钟自身复制一次,复制后所占内存是原来的2倍,那么开机后经过 分钟,该病毒占据64MB内存(1MB=210KB).
9.某人对东北一种松树的生长进行了研究,收集了其高度h(米)与生长时间t(年)的相关数据如下表所示,选择h=mt+b与h=loga(t+1)来拟合h与t的关系,你认为哪个符合 并预测第8年松树的高度.
t(年) 1 2 3 4 5 6
h(米) 0.6 1 1.3 1.5 1.6 1.7
10.某公司承包了一个工程项目,经统计发现该公司在这项工程项目上的月利润P与月份x近似地满足某一函数关系.其中2月到5月所获利润统计如下表:
月份(月) 2 3 4 5
所获利润(亿元) 89 90 89 86
(1)已知该公司的月利润P与月份x近似满足下列中的某一个函数模型:①P(x)=ax2+bx+c;②P(x)=a·bx+c;③P(x)=alogbx+c,请以表中该公司这四个月的利润与月份的数据为依据给出你的选择(需要说明选择该模型的理由),并据此估计该公司8月份在这项工程项目中获得的利润;
(2)根据(1)中选择的函数模型P(x),若该公司承包项目的月成本符合函数模型Q(x)=(单位:亿元),求该公司承包的这项工程项目月成本的最大值及相应的月份.
题组三 不同增长函数模型的图像特征
11.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间后,为了赶时间加快速度行驶.与以上事件吻合得最好的图像是 ( )
12.向高为H的水瓶内注水,一直到注满为止,如果注水量V与水深h的函数图像如图所示,那么水瓶的形状大致是 ( )
13.如图所示的是某受污染的湖泊在自然净化过程中某种有害物质的残留量y与净化时间t(月)的近似函数关系:y=at(t≥0,a>0且a≠1)的图像.有以下叙述:
①第4个月时,残留量就会低于;
②每月减少的有害物质量都相等;
③若残留量为,,时,所经过的时间分别是t1,t2,t3,则t1+t2=t3.
其中所有叙述正确的序号是 .
14.在某种金属材料的耐高温实验中,温度y(℃)随着时间t(min)变化的情况由计算机记录后显示的图像如图所示.现给出下列说法:
①前5min温度增加的速度越来越快;
②前5min温度增加的速度越来越慢;
③5min以后温度保持匀速增加;
④5min以后温度保持不变.
其中说法正确的是 (填序号).
15.函数f(x)=2x和g(x)=x3的图像如图所示.设两函数的图像交于点A(x1,y1),B(x2,y2),且x1
(2)结合函数图像,比较f(6),g(6),f(2017),g(2017)的大小.
能力提升练
一、选择题
1.已知函数y1=2x,y2=x2,y3=log2x,在区间(0,+∞)上一定存在x0,当x>x0时 ( )
A.2x>x2>log2x B.x2>2x>log2x
C.log2x>2x>x2 D.log2x>x2>2x
2.下表是函数值y随自变量x变化的一组数据,由此判断它最可能的函数模型是 ( )
x 4 5 6
y 15 20 15
A.一次函数模型 B.二次函数模型
C.指数函数模型 D.对数函数模型
3.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:万元)对年销售量y(单位:t)的影响,对近6年的年宣传费xi(i=1,2,…,6)和年销售量yi进行整理,得到的数据如下表所示:
x 1.00 2.00 3.00 4.00 5.00 6.00
y 1.65 2.20 2.60 2.76 2.90 3.10
根据上表数据,下列函数中适宜作为年销售量y关于年宣传费x的拟合函数的是 ( )
A.y=0.5(x+1) B.y=log3x+1.5
C.y=2x-1 D.y=2
4.(2021四川江油一中高一上期中)一种放射性元素最初的质量为500g,按每年10%衰减,则这种放射性元素的半衰期约为 年.(注:剩余质量为最初质量的一半,所需的时间叫作半衰期)(结果精确到0.1,参考数据:lg2=0.3010,lg3=0.4771) ( )
A.5.2 B.6.6 C.7.1 D.8.3
5.(2021湖北武汉三中高一上月考)如图所示,液体从一个圆锥形漏斗漏入一个圆柱形桶中,开始时漏斗中盛满液体,经过3秒漏完,圆柱形桶中液面上升速度是一个常量,则漏斗中液面下降的高度H与下降时间t之间的函数关系的图像只可能是 ( )
6.某小型贸易公司为了实现年终10万元利润的目标,特制订了一个销售人员年终绩效奖励方案:当销售利润为x万元(4≤x≤10)时,奖金y(万元)随销售利润x(万元)的增加而增加,但奖金总数不超过2万元,同时不超过销售利润的,则下列函数中,符合该公司奖励方案的函数模型是(参考数据:lg2≈0.3,lg3≈0.48,lg5≈0.7) ( )
A.y=0.4x B.y=lgx+1
C.y= D.y=1.125x
二、填空题
7.(2020四川泸州泸县一中高一下月考)把物体放在空气中冷却,如果物体原来的温度是θ1℃,空气温度是θ0℃,t分钟后温度θ℃可由公式:θ=θ0+(θ1-θ0)·求得,现有60℃的物体放在15℃的空气中冷却,当物体温度降为35℃时,所用冷却时间t= 分钟.
8.(2020广东深圳中学高一上期中)小菲在选修课中了解到艾宾浩斯记忆曲线,为了解自己记忆一组单词的情况,她记录了随后一个月的有关数据,绘制图像,拟合了记忆保持量 y与时间x(天)之间的函数关系:y=
某同学根据小菲拟合后的信息得到以下结论:
①随着时间的增加,小菲的单词记忆保持量降低;
②9天后,小菲的单词记忆保持量低于40%;
③26天后,小菲的单词记忆保持量不足20%.
其中正确的结论序号有 .
三、解答题
9.(2020江西信丰中学高一上期末)某纪念章于2021年元旦开始上市.通过市场调查,得到该纪念章每一枚的市场价y(单位:元)与上市时间x(单位:天)的数据如下表:
上市时间x天 4 10 36
市场价y元 90 51 90
(1)根据上表数据,从下列函数中选择一个恰当的函数模型描述该纪念章的市场价y与上市时间x的关系,并说明理由;
①y=ax+b(a≠0);②y=ax2+bx+c(a≠0);③y=alogbx(b>0,且b≠1).
(2)利用选取的函数,求该纪念章市场价最低时的上市时间及最低的价格.
10.某医药研究所研发的一种新药,成年人按规定的剂量服用后,据监测:服药后每毫升血液中的含药量y(单位:微克)与时间t(单位:小时)之间近似满足如图所示的曲线对应的函数.
(1)写出服药后y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫升血液中含药量不少于1微克时,治疗有效.问:服药多少小时后开始有治疗效果 治疗效果能持续多少小时 (结果精确到0.1,参考数据:lg2≈0.301)
11.攀枝花是一座资源富集的城市,矿产资源储量巨大,已发现矿种76种,探明储量39种,其中钒、钛资源储量分别占全国的63%和93%,占全球的11%和35%,因此其素有“钒钛之都”的美称.攀枝花市某科研单位在研发钛合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值y(y值越大产品的性能越好)与这种新合金材料的含量x(单位:克)的关系为:当0≤x<7时,y是x的二次函数;当x≥7时,y=.测得部分数据如下表:
x(单位:克) 0 2 6 10 …
y -4 8 8 …
(1)求y关于x的函数关系式y=f(x);
(2)求该新合金材料的含量x为何值时产品的性能达到最佳.
12.()某服装批发市场销售季节性流行服装F,当季节即将来临时,价格呈上升趋势,开始时每件定价为120元,并且每周(7天)每件涨价10元(第1周每件定价为120元,第2周每件定价为130元),4周后开始保持每件160元的价格销售;8周后当季节即将过去时,平均每周每件降价10元,直到第12周末,该服装不再销售.
(1)试建立每件售价A与周次t之间的函数关系式;
(2)若此服装每件进价B与周次t之间的关系式为B=问该服装在第几周每件销售利润R最大 并求出最大值.(注:每件销售利润=售价-进价)
参考答案:
基础过关练
1.B 2.A 3.C 4.C 6.D
7.A 11.C 12.B
1.B A、C中函数的增长速度越来越快,D中一次函数的增长速度不变,只有B中对数函数的增长速度越来越慢,符合题意.
2.A 根据已知所给的散点图,观察得到图像在第一象限,且从左到右图像是上升的,并且增长速度越来越快,根据四个选项中函数的增长趋势可得,用指数函数拟合最好,故选A.
3.C 由题表中的数据可以看出,y3增长缓慢,所以是对数型函数;y2增长速度最快,所以是指数型函数;y1的增长速度仅次于y2,是幂型函数.故选C.
4.C 由题表中的数据可知:v随着t的增大而增大,所以B不符合;
对于A,log21.99≈2,log23≈1.6,log24=2,所以A不符合;
对于C,≈1.5,=4,=7.5,≈12.5,≈18.2,所以C符合;
对于D,2×1.99-2=1.98,2×3-2=4,2×4-2=6,2×5.1-2=8.2,2×6.12-2=10.24,D不符合.故选C.
5.解析 (1)由题中的函数图像特征及变化趋势,知曲线C1对应的函数为g(x)=0.3x-1,
曲线C2对应的函数为f(x)=lgx.
(2)当x∈(0,x1)时,g(x)>f(x);当x∈(x1,x2)时,g(x)
g(x)呈直线增长,函数值变化是均匀的,f(x)随着x的增大而逐渐增大,其函数值变化得越来越慢.
6.D 设该林区的森林原有蓄积量为a,由题意知,ax=a(1+0.104)y,故y=log1.104x(x≥1),∴y=f(x)的图像大致为D中的图像.
7.A 设甲、乙两食堂1月份的营业额均为m,甲食堂的营业额每月增加a(a>0),乙食堂的营业额每月增加的百分率为x,由题意可知,m+8a=m×(1+x)8,则5月份甲食堂的营业额y1=m+4a,乙食堂的营业额y2=m×(1+x)4=.因为-=(m+4a)2-m(m+8a)=16a2>0,所以y1>y2,故该年5月份甲食堂的营业额较高.
8.答案 45
解析 设开机后经过n个3分钟,该病毒占据64MB内存,
则2×2n=64×210=216,解得n=15,故时间为15×3=45(分钟).
9.解析 根据题表中数据作出散点图如图.
由图像可以看出增长的速度越来越慢,用一次函数模型拟合不合适,选用对数函数模型比较合理.
不妨将(2,1)代入h=loga(t+1)中,得1=loga3,解得a=3.
故可用函数h=log3(t+1)来拟合这个实际问题.
当t=8时,求得h=log3(8+1)=2(米),
故可预测第8年松树的高度为2米.
10.解析 (1)易知a≠0,因为P(x)=a·bx+c,P(x)=alogbx+c为单调函数,由所给数据知,满足条件的函数不单调,所以选取P(x)=ax2+bx+c进行描述.
将题表中(2,89),(3,90),(4,89)代入P(x),得到解方程组得所以该公司月利润P与月份x近似满足的函数为P(x)=-x2+6x+81,x∈[1,12],x∈N+,
当x=8时,得P=65(亿元).
所以8月份所获得的利润约为65亿元.
(2)由(1)得,Q(x)=
=.当x=2时,Q(x)max=11.
所以该公司承包的这项工程项目月成本的最大值为11亿元,相应的月份为2月.
11.C 开始时小明匀速行驶,所得图像为一条直线,且距离学校越来越近,故排除A.因交通堵塞停留了一段时间,与学校的距离不变,故排除D.后来为了赶时间加快速度行驶,故排除B.故选C.
12.B 水深h为自变量,随着h的增大,A中V的增长速度越来越快,C中先慢后快再慢,D中增长速度不变,只有B中V的增长速度越来越慢.故选B.
13.答案 ①③
解析 根据题意,函数的图像经过点2,,故函数为y=.易知①③正确.
14.答案 ②④
解析 因为温度y关于时间t的图像是先凸后平,所以前5min每当t增加一个单位时,相应的增量Δy越来越小,而5min后y关于t的增量保持为0,所以②④正确.
15.解析 (1)曲线C1对应的函数为g(x)=x3,曲线C2对应的函数为f(x)=2x.
(2)∵f(1)=2>g(1)=1,f(2)=4
∴f(2017)>g(2017).
又g(2017)>g(6),
∴f(2017)>g(2017)>g(6)>f(6).
能力提升练
1.A 2.B 3.B 4.B 5.B
6.B
一、选择题
1.A 由于指数函数增长最快,对数函数增长最慢,因此当x很大时,指数函数值最大,对数函数值最小,即在区间(0,+∞)上一定存在x0,当x>x0时,2x>x2>log2x,故选A.
2.B 当自变量x由4增大到5时,函数值y由15增大到20;当自变量x由5增大到6时,函数值y由20减小到15.因此函数不是单调函数,从而函数模型不可能是一次函数模型、指数函数模型和对数函数模型,故选B.
3.B 由题表知,当自变量增加1个单位时,函数值依次增加0.55、0.40、0.16、0.14、0.20,因此A、C不符合题意;当x取1、4时,y=2的值分别为2、4,与题表中的数据相差较大,故选B.
4.B 设这种放射性元素的半衰期为x年,则500(1-10%)x=250,
所以(1-10%)x=,所以log0.9=x,
所以x=lo2,
所以x=,
所以x=,
所以x=≈6.6.
故选B.
解题模板
求解和对数有关的实际问题的思路:
(1)根据题设条件列出符合的关于待求量的等式;
(2)利用指对互化、对数运算法则以及对数运算性质、对数换底公式求出待求量的值.
5.B 由于所给的圆锥形漏斗上口大于下口,
当时间取t时,漏斗中液面下落的高度不
会达到漏斗高度的,对比四个选项的图像可得结果.
故选B.
6.B A选项中,当x=10时,y=4,超过2万元,故A不符合;B选项中,y=lgx+1在[4,10]上是增函数,x=10时,ymax=2,结合图像(如图)知:lgx+1<在x∈[4,10]上恒成立,故B符合;
C选项中,当x=10时,y=>2,超过2万元,故C不符合;
D选项中,当x=10时,y=,设=a,则lga=10(lg9-lg8)≈0.6,
因此a≈100.6>>2,超过2万元,故D不符合.故选B.
二、填空题
7.答案 2
解析 由题意,得θ0=15℃,θ1=60℃,θ=35℃,
∵θ=θ0+(θ1-θ0)·,
∴35=15+(60-15)·,
∴====,
解得t=2.
8.答案 ①②
解析 由y=
可得y随着x的增加而减少,故①正确;
当1
三、解答题
9.信息提取 ①当x=4,10,36时,y依次为90,51,90;②给出三个函数模型,选择一个恰当的函数模型描述该纪念章的市场价y与上市时间x的关系.
数学建模 本题以经济生活中纪念章的市场价的估算为背景,建立函数模型,通过比较函数值增长的快慢选择最恰当的函数模型进行估算.求解时,首先确定三种模型的解析式,分析、验证函数模型,找出最接近的函数模型.
解析 (1)∵随着时间x的增加,y的值先减后增,
而所给的三个函数中,y=ax+b(a≠0)和y=alogbx(b>0,且b≠1)显然都是单调函数,不满足题意,
∴选取y=ax2+bx+c(a≠0).
(2)由题知,把点(4,90),(10,51),(36,90)代入y=ax2+bx+c中,
得解得a=,b=-10,c=126,
∴y=x2-10x+126=(x-20)2+26,
∴当x=20时,ymin=26.
故该纪念章市场价最低时的上市时间为20天,最低的价格为26元.
10.解析 (1)根据题中图像知:当0≤t<1时,y=4t;
当t≥1时,y=a·0.8t,由t=1时,y=4得4=a·0.8,所以a=5,即y=5×0.8t.
因此y=
(2)根据题意,由4t≥1(0≤t<1),解得0.25≤t<1;由5×0.8t≥1(t≥1),得0.8t≥0.2,
所以1≤t≤==≈7.21,
所以0.25≤t≤7.21,
又7.21-0.25=6.96≈7.0,
所以服药0.25小时(即15分钟)后开始有治疗效果,治疗效果能持续7.0小时.
11.解析 (1)当0≤x<7时,y是x的二次函数,可设y=ax2+bx+c(a≠0),
由x=0,y=-4可得c=-4,
由x=2,y=8,可得4a+2b=12,
由x=6,y=8,可得36a+6b=12,
解得a=-1,b=8,即有y=-x2+8x-4;
当x≥7时,y=,由x=10,y=,可得m=8,即有y=.
综上可得,y=
(2)当0≤x<7时,y=-x2+8x-4=-(x-4)2+12,
所以当x=4时,y取得最大值12;
当x≥7时,y=递减,可得y≤3,
所以当x=7时,y取得最大值3.
综上可得,当x=4时产品的性能达到最佳.
12.解析 (1)根据题意计算得:
当t∈(0,4]且t∈N+时,A=110+10t;当t∈(4,8]且t∈N+时,A=160;
当t∈(8,12]且t∈N+时,A=240-10t.
故A=
(2)因为每件销售利润=售价-进价,所以R=A-B,
当t∈(0,4]且t∈N+时,R=4t+30,
t=4时,Rmax=46;
当t∈(4,8]且t∈N+时,R=56;
当t∈(8,12]且t∈N+时,R=136-10t,t=9时,Rmax=46.
故该服装在第5,6,7,8周每件销售利润R最大,最大值是56元.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
