2023届高考数学复习专题 空间角与距离、空间向量及应用(共21张PPT)
文档属性
| 名称 | 2023届高考数学复习专题 空间角与距离、空间向量及应用(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 15:08:44 | ||
图片预览








文档简介
(共21张PPT)
第八章 立体几何与空间向量
8.4 空间角与距离、空间向量及应用
2023届高考数学复习专题 ★★
考点清单
考点一 空间角与距离
1.空间角
(1)异面直线所成角的范围是 ;线面角的范围是 ;二面角的范围是[0,π].
(2)求解异面直线所成角有两种方法:平移法、向量法,应用时应注意异面直线所成角的范围.
(3)用向量法求解斜线与平面所成角的问题,关键是确定斜线的一个方向向量a和平面的一个法向
量b,再通过计算线面角的向量公式sin θ=|cos|= (θ是斜线与平面所成的角)求解,要特别
注意a和b的夹角与线面角的关系.
(4)利用向量法求二面角的大小时,应注意二面角的大小与两半平面的法向量夹角大小的关系,它
们之间可能相等,也可能互补,故应在分清关系的情况下求解,避免出现错误.
(5)计算二面角的关键是作出二面角的平面角,方法较为灵活,可以通过“割”或“补”找二面角
的平面角.对于无棱二面角,可以先找出棱或借助于向量法求解,也可以利用射影面积公式cos θ=
(θ是二面角的平面角)求解.
2.求空间距离常用的方法:
(1)直接法(找所求距离对应的垂线段):利用线线垂直、线面垂直、面面垂直等性质定理和判定定
理,作出空间距离对应的垂线段,再通过解三角形求出距离.其中,找垂足是作垂线段的关键,一般借
助面面垂直的性质定理或线面垂直的判定定理作出面的垂线,因此要充分挖掘条件中的垂直关系.
(2)间接法:在求解线面距离、面面距离的问题时,都可以转化为点面距离求解.在求解点面距离时,
可以转化为点线距离,也可以利用等体积转化法或等比例转化法进行求解;在求解点线距离时,可
以利用勾股定理求解,也可以构造三角形采用等面积转化法求解.
● 拓展
与线面角有关的问题
(1)求斜线与平面所成的角的关键是:找到斜线在平面内的射影,斜线与其射影所成的锐角即为斜
线与平面所成的角.
(2)最小角定理:平面的斜线和它在平面内的射影所成的角是这条斜线和这个平面内任一条直线所
成的角中最小的角.
(3)三余弦公式:cos θ=cos θ1cos θ2(如图所示,其中θ1是斜线OA与平面α所成的角,θ2是斜线OA的射影
AB与平面内的直线AC的夹角,θ是斜线OA与平面内的直线AC的夹角).
(4)点C是∠APB所在平面外的一点,若∠CPA=∠CPB≠90°,则斜线CP在平面APB内的射影落在
∠APB的平分线上.
考点二 空间向量及其应用
1.与空间向量运算有关的结论
设a=(a1,a2,a3),b=(b1,b2,b3),b≠0.
(1)a∥b a=λb a1=λb1,a2=λb2,a3=λb3(λ∈R);
(2)a⊥b a·b=0 a1b1+a2b2+a3b3=0;
(3)|a|= = ;
(4)cos=
= .
2.用向量证明空间中的平行关系
(1)设直线l1和l2的方向向量分别为v1和v2,则l1∥l2(或l1与l2重合) v1∥v2.
(2)设直线l的方向向量为v,与平面α共面的两个不共线向量分别为v1和v2,则l∥α或l α 存在两个
实数x,y,使v=xv1+yv2.
(3)设直线l的方向向量为v,平面α的法向量为u,则l∥α或l α v⊥u.
(4)设平面α,β的法向量分别为u1,u2,则α∥β u1∥u2.
3.用向量证明空间中的垂直关系
(1)设直线l1和l2的方向向量分别为v1和v2,则l1⊥l2 v1⊥v2 v1·v2=0.
(2)设直线l的方向向量为v,平面α的法向量为u,则l⊥α v∥u.
(3)设平面α和β的法向量分别为u1和u2,则α⊥β u1⊥u2 u1·u2=0.
4.用空间向量解决空间角
(1)设异面直线l1,l2的方向向量分别为m1,m2,则l1与l2所成的角θ满足cos θ=|cos|.
(2)设直线l的方向向量和平面α的法向量分别为m和n,则直线l与平面α所成角θ满足sin θ=|cos|.
(3)求二面角的大小
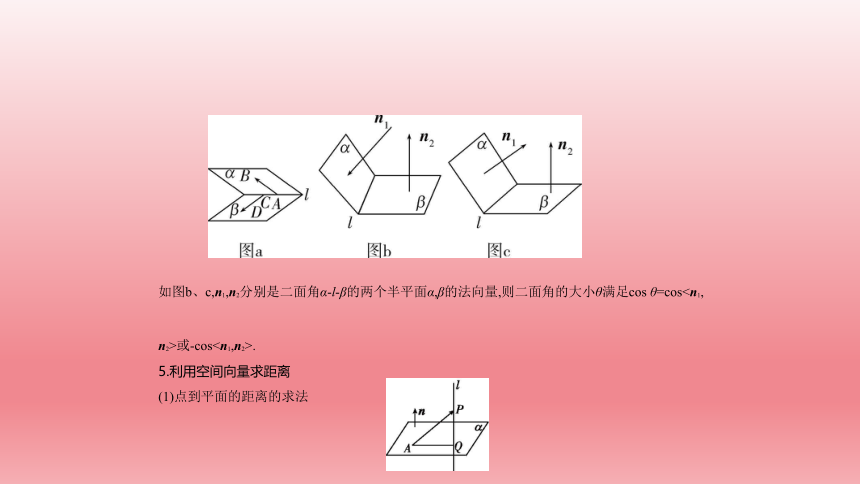
如图a,AB、CD是二面角α-l-β的两个半平面内与棱l垂直的直线,则二面角的大小θ=< , >.
如图b、c,n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小θ满足cos θ=cosn2>或-cos.
5.利用空间向量求距离
(1)点到平面的距离的求法
设点P为平面α外一点,点A是平面α内的定点,则求点到平面的距离的步骤:
①求平面α的一个法向量n;
②求向量 ;
③求向量 在法向量n上投影的绝对值,即为点P到平面α的距离.
(2)直线到平面的距离的求法
当直线与平面平行时,才能求线面距离,此时直线上任一点到平面的距离都相等,即为直线到平面
的距离,故可通过求点面距离来求线面距离.
(3)两平行平面间的距离的求法
两平行平面间的距离可转化为点到平面的距离来解决.
题型方法
一、求解异面直线所成角的方法
1.定义法(平移法)
(1)平移:①利用图中已有的平行线平移;②利用特殊点(线段的端点或中点)作平行线平移;③补形
平移;
(2)证明:证明所作的角是异面直线所成的角或其补角;
(3)寻找:在立体图形中,寻找或者作出含有此角的三角形,并解之;
(4)取舍:所作的角为钝角时,应取它的补角作为异面直线所成的角.
2.向量法
建立空间直角坐标系后,确定两直线的方向向量a,b,则两异面直线所成角θ满足cos θ= .
例1 (2021全国乙,5,5分)在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为
( )
A. B. C. D.
解析 如图所示,连接BC1,C1P,
D
易知四边形ABC1D1是平行四边形,
∴BC1∥AD1,
∴∠C1BP(或其补角)就是异面直线AD1与BP所成的角,
设正方体的棱长为a,则BC1= a,C1P= a,连接AC,BD,设AC交BD于点O,连接OP,则OP⊥平面
ABCD,
∵OB 平面ABCD,∴OP⊥OB,
∴PB= = a.
在△C1BP中,cos∠PBC1= = ,
∴∠PBC1= ,
即直线PB与AD1所成的角为 .故选D.
二、求解直线与平面所成角的方法
1.定义法
(1)作:在斜线上选取恰当的点,过该点向平面引垂线,作出所求角,其中确定垂足的位置是关键;
(2)证:证明所作的角为直线与平面所成的角;(3)求:构造角所在的三角形,利用解三角形的知识求角.
2.公式法
sin θ= (其中h为斜线上除斜足外的任一点到所给平面α的距离,l为该点到斜足的距离,θ为斜线与
平面α所成的角).
3.向量法
sin θ=|cos< ,n>|= (其中AB为平面α的斜线,n为平面α的法向量,θ为斜线与平面α所成的角).
例2 (2018浙江,19,15分)如图,已知多面体ABCA1B1C1中,A1A,B1B,C1C均垂直于平面ABC,∠ABC=
120°,A1A=4,C1C=1,AB=BC=B1B=2.
(1)证明:AB1⊥平面A1B1C1;
(2)求直线AC1与平面ABB1所成的角的正弦值.
解析 解法一:
(1)证明:由AB=2,AA1=4,BB1=2,AA1⊥AB,BB1⊥AB得AB1=A1B1=2 ,所以A1 +A =A ,
故AB1⊥A1B1.(利用勾股定理的逆定理证明线线垂直)
由BC=2,BB1=2,CC1=1,BB1⊥BC,CC1⊥BC得B1C1= ,
由AB=BC=2,∠ABC=120°得AC=2 ,
由CC1⊥AC,得AC1= ,所以A +B1 =A ,
故AB1⊥B1C1.又A1B1∩B1C1=B1,因此AB1⊥平面A1B1C1.
(2)如图,过点C1作C1D⊥A1B1,交直线A1B1于点D,连接AD.由AB1⊥平面A1B1C1且AB1 平面ABB1得平
面A1B1C1⊥平面ABB1,由C1D⊥A1B1得C1D⊥平面ABB1,所以∠C1AD是AC1与平面ABB1所成的角.(利
用定义法找线面角的关键是构造线面垂直)由B1C1= ,A1B1=2 ,A1C1= 得cos∠C1A1B1= ,则
sin∠C1A1B1= ,
所以C1D= ,
故sin∠C1AD= = .
因此,直线AC1与平面ABB1所成的角的正弦值是 .
解法二:
(1)证明:如图,以AC的中点O为原点,分别以射线OB,OC为x,y轴的非负半轴,建立空间直角坐标系O-
xyz.(建立空间直角坐标系)
由题意知各点坐标如下:
A(0,- ,0),B(1,0,0),A1(0,- ,4),B1(1,0,2),C1(0, ,1).因此 =(1, ,2), =(1, ,-2), =(0,2 ,
-3).由 · =0得AB1⊥A1B1.由 · =0得AB1⊥A1C1.(注意两向量垂直的充要条件的应用)
因为A1B1∩A1C1=A1,所以AB1⊥平面A1B1C1.
(2)设直线AC1与平面ABB1所成的角为θ.
由(1)可知 =(0,2 ,1), =(1, ,0), =(0,0,2).
设平面ABB1的法向量为n=(x,y,z).
由 得 可取n=(- ,1,0).
所以sin θ=|cos< ,n>|= = .(注意线面角θ与两向量夹角的关系)
因此,直线AC1与平面ABB1所成的角的正弦值是 .
三、求解二面角的方法
(一)通过找二面角的平面角进行求解
1.定义法:在二面角的棱上找一特殊点,过该点在两个半平面内分别作垂直于棱的射线,如图(1),
∠AOB为二面角α-l-β的平面角.
2.垂面法:过棱上任一点作棱的垂直平面,该平面与二面角的两个半平面的交线所形成的角即为二
面角的平面角,如图(2),∠AOB为二面角α-l-β的平面角.
3.垂线法(三垂线定理法):过二面角的一个半平面内一点作另一个半平面所在平面的垂线,从垂足
出发向棱引垂线,利用三垂线定理即可找到所求二面角的平面角或其补角,如图(3),∠ABO为二面
角α-l-β的平面角.
(二)利用公式进行求解
1.射影面积公式:cos θ= ,该方法主要用来解决无棱二面角大小的计算,关键在于找出其中一个
半平面内的多边形在另一个半平面内的射影.
2.向量法:利用公式cos= (n1,n2分别为两平面的法向量)进行求解,注意与二面角
大小的关系,是相等还是互补,需结合图形进行判断.
例3 (2017山东理,17,12分)如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所
在直线为旋转轴旋转120°得到的,G是 的中点.
(1)设P是 上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
解析 (1)因为AP⊥BE,AB⊥BE,AB,AP 平面ABP,AB∩AP=A,所以BE⊥平面ABP,又BP 平面
ABP,
所以BE⊥BP,又∠EBC=120°,因此∠CBP=30°.
(2)以B为坐标原点,分别以BE,BP,BA所在的直线为x,y,z轴,建立如图所示的空间直角坐标系.
由题意得A(0,0,3),E(2,0,0),G(1, ,3),C(-1, ,0),
故 =(2,0,-3), =(1, ,0), =(2,0,3),
设m=(x1,y1,z1)是平面AEG的法向量.
由
可得
取z1=2,可得平面AEG的一个法向量m=(3,- ,2).
设n=(x2,y2,z2)是平面ACG的法向量.
由
可得
取z2=-2,可得平面ACG的一个法向量n=(3,- ,-2).
所以cos= = .
易知所求角为锐二面角,因此所求的角为60°.
第八章 立体几何与空间向量
8.4 空间角与距离、空间向量及应用
2023届高考数学复习专题 ★★
考点清单
考点一 空间角与距离
1.空间角
(1)异面直线所成角的范围是 ;线面角的范围是 ;二面角的范围是[0,π].
(2)求解异面直线所成角有两种方法:平移法、向量法,应用时应注意异面直线所成角的范围.
(3)用向量法求解斜线与平面所成角的问题,关键是确定斜线的一个方向向量a和平面的一个法向
量b,再通过计算线面角的向量公式sin θ=|cos
注意a和b的夹角与线面角的关系.
(4)利用向量法求二面角的大小时,应注意二面角的大小与两半平面的法向量夹角大小的关系,它
们之间可能相等,也可能互补,故应在分清关系的情况下求解,避免出现错误.
(5)计算二面角的关键是作出二面角的平面角,方法较为灵活,可以通过“割”或“补”找二面角
的平面角.对于无棱二面角,可以先找出棱或借助于向量法求解,也可以利用射影面积公式cos θ=
(θ是二面角的平面角)求解.
2.求空间距离常用的方法:
(1)直接法(找所求距离对应的垂线段):利用线线垂直、线面垂直、面面垂直等性质定理和判定定
理,作出空间距离对应的垂线段,再通过解三角形求出距离.其中,找垂足是作垂线段的关键,一般借
助面面垂直的性质定理或线面垂直的判定定理作出面的垂线,因此要充分挖掘条件中的垂直关系.
(2)间接法:在求解线面距离、面面距离的问题时,都可以转化为点面距离求解.在求解点面距离时,
可以转化为点线距离,也可以利用等体积转化法或等比例转化法进行求解;在求解点线距离时,可
以利用勾股定理求解,也可以构造三角形采用等面积转化法求解.
● 拓展
与线面角有关的问题
(1)求斜线与平面所成的角的关键是:找到斜线在平面内的射影,斜线与其射影所成的锐角即为斜
线与平面所成的角.
(2)最小角定理:平面的斜线和它在平面内的射影所成的角是这条斜线和这个平面内任一条直线所
成的角中最小的角.
(3)三余弦公式:cos θ=cos θ1cos θ2(如图所示,其中θ1是斜线OA与平面α所成的角,θ2是斜线OA的射影
AB与平面内的直线AC的夹角,θ是斜线OA与平面内的直线AC的夹角).
(4)点C是∠APB所在平面外的一点,若∠CPA=∠CPB≠90°,则斜线CP在平面APB内的射影落在
∠APB的平分线上.
考点二 空间向量及其应用
1.与空间向量运算有关的结论
设a=(a1,a2,a3),b=(b1,b2,b3),b≠0.
(1)a∥b a=λb a1=λb1,a2=λb2,a3=λb3(λ∈R);
(2)a⊥b a·b=0 a1b1+a2b2+a3b3=0;
(3)|a|= = ;
(4)cos
= .
2.用向量证明空间中的平行关系
(1)设直线l1和l2的方向向量分别为v1和v2,则l1∥l2(或l1与l2重合) v1∥v2.
(2)设直线l的方向向量为v,与平面α共面的两个不共线向量分别为v1和v2,则l∥α或l α 存在两个
实数x,y,使v=xv1+yv2.
(3)设直线l的方向向量为v,平面α的法向量为u,则l∥α或l α v⊥u.
(4)设平面α,β的法向量分别为u1,u2,则α∥β u1∥u2.
3.用向量证明空间中的垂直关系
(1)设直线l1和l2的方向向量分别为v1和v2,则l1⊥l2 v1⊥v2 v1·v2=0.
(2)设直线l的方向向量为v,平面α的法向量为u,则l⊥α v∥u.
(3)设平面α和β的法向量分别为u1和u2,则α⊥β u1⊥u2 u1·u2=0.
4.用空间向量解决空间角
(1)设异面直线l1,l2的方向向量分别为m1,m2,则l1与l2所成的角θ满足cos θ=|cos
(2)设直线l的方向向量和平面α的法向量分别为m和n,则直线l与平面α所成角θ满足sin θ=|cos
(3)求二面角的大小
如图a,AB、CD是二面角α-l-β的两个半平面内与棱l垂直的直线,则二面角的大小θ=< , >.
如图b、c,n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小θ满足cos θ=cos
5.利用空间向量求距离
(1)点到平面的距离的求法
设点P为平面α外一点,点A是平面α内的定点,则求点到平面的距离的步骤:
①求平面α的一个法向量n;
②求向量 ;
③求向量 在法向量n上投影的绝对值,即为点P到平面α的距离.
(2)直线到平面的距离的求法
当直线与平面平行时,才能求线面距离,此时直线上任一点到平面的距离都相等,即为直线到平面
的距离,故可通过求点面距离来求线面距离.
(3)两平行平面间的距离的求法
两平行平面间的距离可转化为点到平面的距离来解决.
题型方法
一、求解异面直线所成角的方法
1.定义法(平移法)
(1)平移:①利用图中已有的平行线平移;②利用特殊点(线段的端点或中点)作平行线平移;③补形
平移;
(2)证明:证明所作的角是异面直线所成的角或其补角;
(3)寻找:在立体图形中,寻找或者作出含有此角的三角形,并解之;
(4)取舍:所作的角为钝角时,应取它的补角作为异面直线所成的角.
2.向量法
建立空间直角坐标系后,确定两直线的方向向量a,b,则两异面直线所成角θ满足cos θ= .
例1 (2021全国乙,5,5分)在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为
( )
A. B. C. D.
解析 如图所示,连接BC1,C1P,
D
易知四边形ABC1D1是平行四边形,
∴BC1∥AD1,
∴∠C1BP(或其补角)就是异面直线AD1与BP所成的角,
设正方体的棱长为a,则BC1= a,C1P= a,连接AC,BD,设AC交BD于点O,连接OP,则OP⊥平面
ABCD,
∵OB 平面ABCD,∴OP⊥OB,
∴PB= = a.
在△C1BP中,cos∠PBC1= = ,
∴∠PBC1= ,
即直线PB与AD1所成的角为 .故选D.
二、求解直线与平面所成角的方法
1.定义法
(1)作:在斜线上选取恰当的点,过该点向平面引垂线,作出所求角,其中确定垂足的位置是关键;
(2)证:证明所作的角为直线与平面所成的角;(3)求:构造角所在的三角形,利用解三角形的知识求角.
2.公式法
sin θ= (其中h为斜线上除斜足外的任一点到所给平面α的距离,l为该点到斜足的距离,θ为斜线与
平面α所成的角).
3.向量法
sin θ=|cos< ,n>|= (其中AB为平面α的斜线,n为平面α的法向量,θ为斜线与平面α所成的角).
例2 (2018浙江,19,15分)如图,已知多面体ABCA1B1C1中,A1A,B1B,C1C均垂直于平面ABC,∠ABC=
120°,A1A=4,C1C=1,AB=BC=B1B=2.
(1)证明:AB1⊥平面A1B1C1;
(2)求直线AC1与平面ABB1所成的角的正弦值.
解析 解法一:
(1)证明:由AB=2,AA1=4,BB1=2,AA1⊥AB,BB1⊥AB得AB1=A1B1=2 ,所以A1 +A =A ,
故AB1⊥A1B1.(利用勾股定理的逆定理证明线线垂直)
由BC=2,BB1=2,CC1=1,BB1⊥BC,CC1⊥BC得B1C1= ,
由AB=BC=2,∠ABC=120°得AC=2 ,
由CC1⊥AC,得AC1= ,所以A +B1 =A ,
故AB1⊥B1C1.又A1B1∩B1C1=B1,因此AB1⊥平面A1B1C1.
(2)如图,过点C1作C1D⊥A1B1,交直线A1B1于点D,连接AD.由AB1⊥平面A1B1C1且AB1 平面ABB1得平
面A1B1C1⊥平面ABB1,由C1D⊥A1B1得C1D⊥平面ABB1,所以∠C1AD是AC1与平面ABB1所成的角.(利
用定义法找线面角的关键是构造线面垂直)由B1C1= ,A1B1=2 ,A1C1= 得cos∠C1A1B1= ,则
sin∠C1A1B1= ,
所以C1D= ,
故sin∠C1AD= = .
因此,直线AC1与平面ABB1所成的角的正弦值是 .
解法二:
(1)证明:如图,以AC的中点O为原点,分别以射线OB,OC为x,y轴的非负半轴,建立空间直角坐标系O-
xyz.(建立空间直角坐标系)
由题意知各点坐标如下:
A(0,- ,0),B(1,0,0),A1(0,- ,4),B1(1,0,2),C1(0, ,1).因此 =(1, ,2), =(1, ,-2), =(0,2 ,
-3).由 · =0得AB1⊥A1B1.由 · =0得AB1⊥A1C1.(注意两向量垂直的充要条件的应用)
因为A1B1∩A1C1=A1,所以AB1⊥平面A1B1C1.
(2)设直线AC1与平面ABB1所成的角为θ.
由(1)可知 =(0,2 ,1), =(1, ,0), =(0,0,2).
设平面ABB1的法向量为n=(x,y,z).
由 得 可取n=(- ,1,0).
所以sin θ=|cos< ,n>|= = .(注意线面角θ与两向量夹角的关系)
因此,直线AC1与平面ABB1所成的角的正弦值是 .
三、求解二面角的方法
(一)通过找二面角的平面角进行求解
1.定义法:在二面角的棱上找一特殊点,过该点在两个半平面内分别作垂直于棱的射线,如图(1),
∠AOB为二面角α-l-β的平面角.
2.垂面法:过棱上任一点作棱的垂直平面,该平面与二面角的两个半平面的交线所形成的角即为二
面角的平面角,如图(2),∠AOB为二面角α-l-β的平面角.
3.垂线法(三垂线定理法):过二面角的一个半平面内一点作另一个半平面所在平面的垂线,从垂足
出发向棱引垂线,利用三垂线定理即可找到所求二面角的平面角或其补角,如图(3),∠ABO为二面
角α-l-β的平面角.
(二)利用公式进行求解
1.射影面积公式:cos θ= ,该方法主要用来解决无棱二面角大小的计算,关键在于找出其中一个
半平面内的多边形在另一个半平面内的射影.
2.向量法:利用公式cos
大小的关系,是相等还是互补,需结合图形进行判断.
例3 (2017山东理,17,12分)如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所
在直线为旋转轴旋转120°得到的,G是 的中点.
(1)设P是 上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
解析 (1)因为AP⊥BE,AB⊥BE,AB,AP 平面ABP,AB∩AP=A,所以BE⊥平面ABP,又BP 平面
ABP,
所以BE⊥BP,又∠EBC=120°,因此∠CBP=30°.
(2)以B为坐标原点,分别以BE,BP,BA所在的直线为x,y,z轴,建立如图所示的空间直角坐标系.
由题意得A(0,0,3),E(2,0,0),G(1, ,3),C(-1, ,0),
故 =(2,0,-3), =(1, ,0), =(2,0,3),
设m=(x1,y1,z1)是平面AEG的法向量.
由
可得
取z1=2,可得平面AEG的一个法向量m=(3,- ,2).
设n=(x2,y2,z2)是平面ACG的法向量.
由
可得
取z2=-2,可得平面ACG的一个法向量n=(3,- ,-2).
所以cos
易知所求角为锐二面角,因此所求的角为60°.
同课章节目录
