北师大版九年级数学下册试题 第二章 二次函数 复习卷 (含答案)
文档属性
| 名称 | 北师大版九年级数学下册试题 第二章 二次函数 复习卷 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 706.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 09:42:37 | ||
图片预览


文档简介
第二章 《二次函数》复习卷
一、选择题。
1.如图,用绳子围成周长为10m的矩形,记矩形的一边长为,它的邻边长为,矩形的面积为.当x在一定范围内变化时,y和S都随x的变化而变化,则y与x,S与x满足的函数关系分别是( )
A.一次函数关系,二次函数关系 B.正比例函数关系,二次函数关系
C.一次函数关系,正比例函数关系 D.正比例函数关系,一次函数关系
2.对于二次函数y=﹣(x﹣1)2+4,下列说法不正确的是( )
A.当x=1时,y有最大值3
B.当x≥1时,y随x的增大而减小
C.开口向下
D.函数图象与x轴交于点(1,0)和(3,0)
3.函数y=ax+1与y=ax2+bx+1(a≠0)的图象可能是( )
A.B.
C.D.
4.已知抛物线上的部分点的横坐标与纵坐标的对应值如表:
… …
… …
以上结论正确的是( )
A.抛物线的开口向下 B.当时,随增大而增大
C.方程的根为或 D.当时,的取值范围
5.已知二次函数y=﹣(x﹣a)2+a﹣1(m为常数),则对如下两个结论的判断正确的是( )
①不论a为何值,函数图象的顶点始终在一条直线上;
②当﹣1<x<2时,y随x的增大而增大,则a的取值范围为a≥2.
A.两个都对 B.两个都错 C.①对②错 D.①错②对
6.如图, 在平面直角坐标系中放置, 点.现将 沿 轴的正方向无滑动翻转,依次得到 连续翻转 14 次, 则经过三顶点的抛物线解析式为( )
A. B.
C. D.
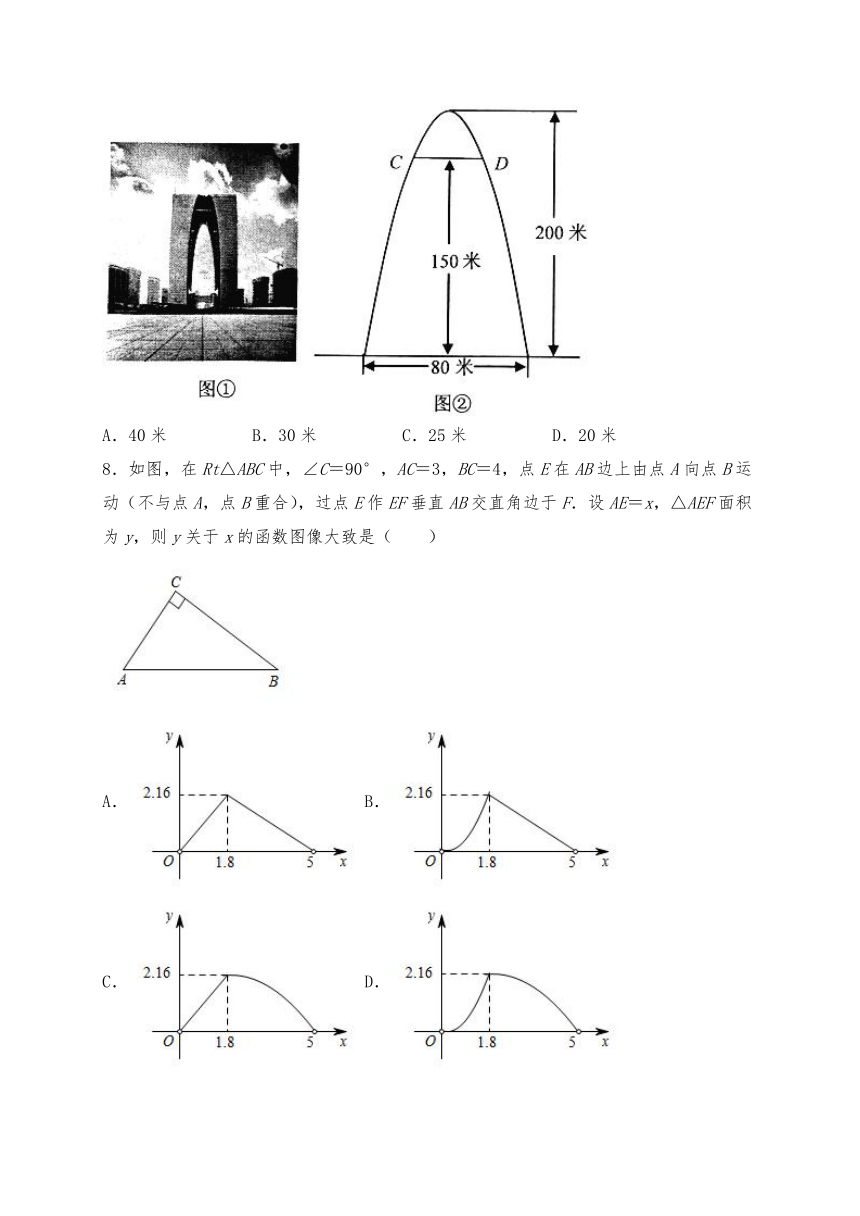
7.如图①,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图②,“门”的内侧曲线呈抛物线形,已知其底部宽度为80米,高度为200米.则离地面150米处的水平宽度(即CD的长)为( )
A.40米 B.30米 C.25米 D.20米
8.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E在AB边上由点A向点B运动(不与点A,点B重合),过点E作EF垂直AB交直角边于F.设AE=x,△AEF面积为y,则y关于x的函数图像大致是( )
A.B.
C.D.
二、填空题。
9.若y=(m﹣2)是关于x的二次函数,则常数m的值为_________.
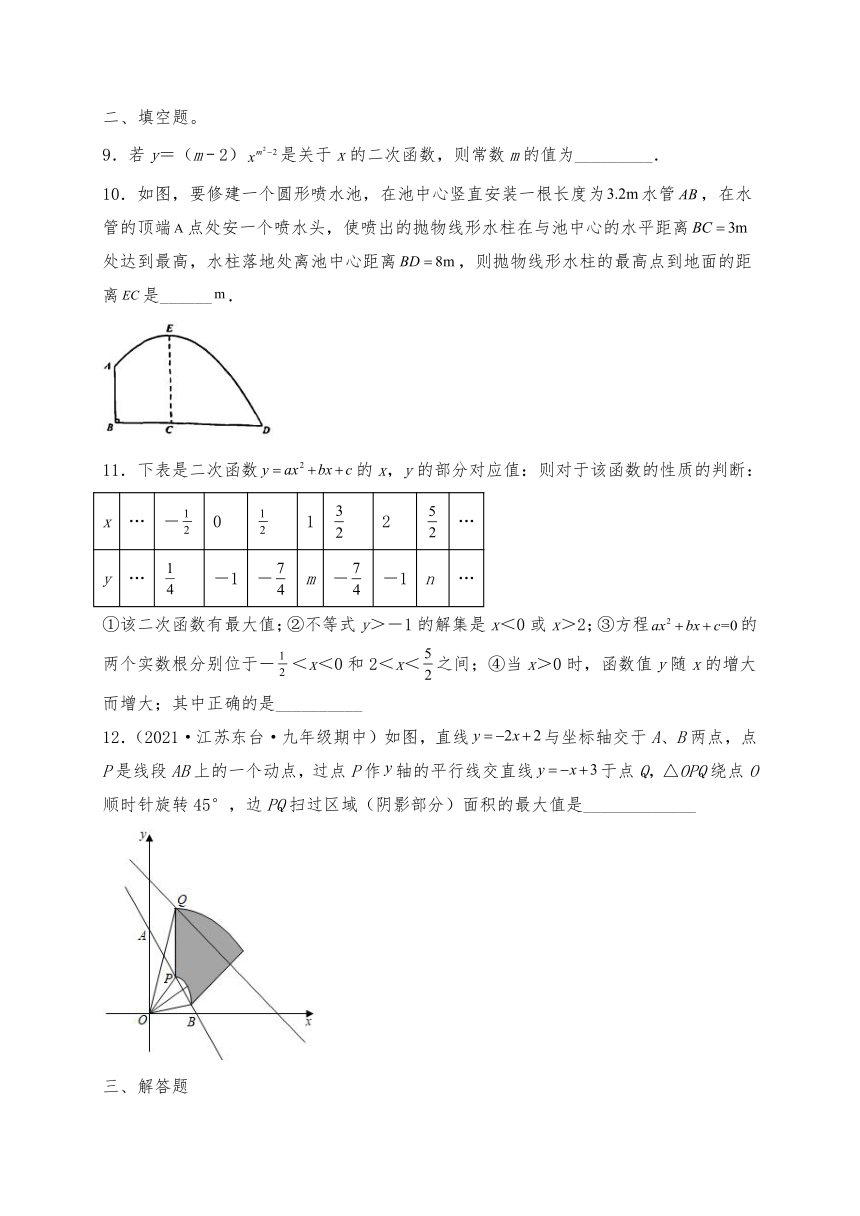
10.如图,要修建一个圆形喷水池,在池中心竖直安装一根长度为水管,在水管的顶端点处安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离处达到最高,水柱落地处离池中心距离,则抛物线形水柱的最高点到地面的距离是______.
11.下表是二次函数的x,y的部分对应值:则对于该函数的性质的判断:
x … - 0 1 2 …
y … -1 - m - -1 n …
①该二次函数有最大值;②不等式y>-1的解集是x<0或x>2;③方程的两个实数根分别位于-<x<0和2<x<之间;④当x>0时,函数值y随x的增大而增大;其中正确的是__________
12.(2021·江苏东台·九年级期中)如图,直线与坐标轴交于A、B两点,点P是线段AB上的一个动点,过点P作轴的平行线交直线于点Q,△OPQ绕点O顺时针旋转45°,边PQ扫过区域(阴影部分)面积的最大值是_____________
三、解答题
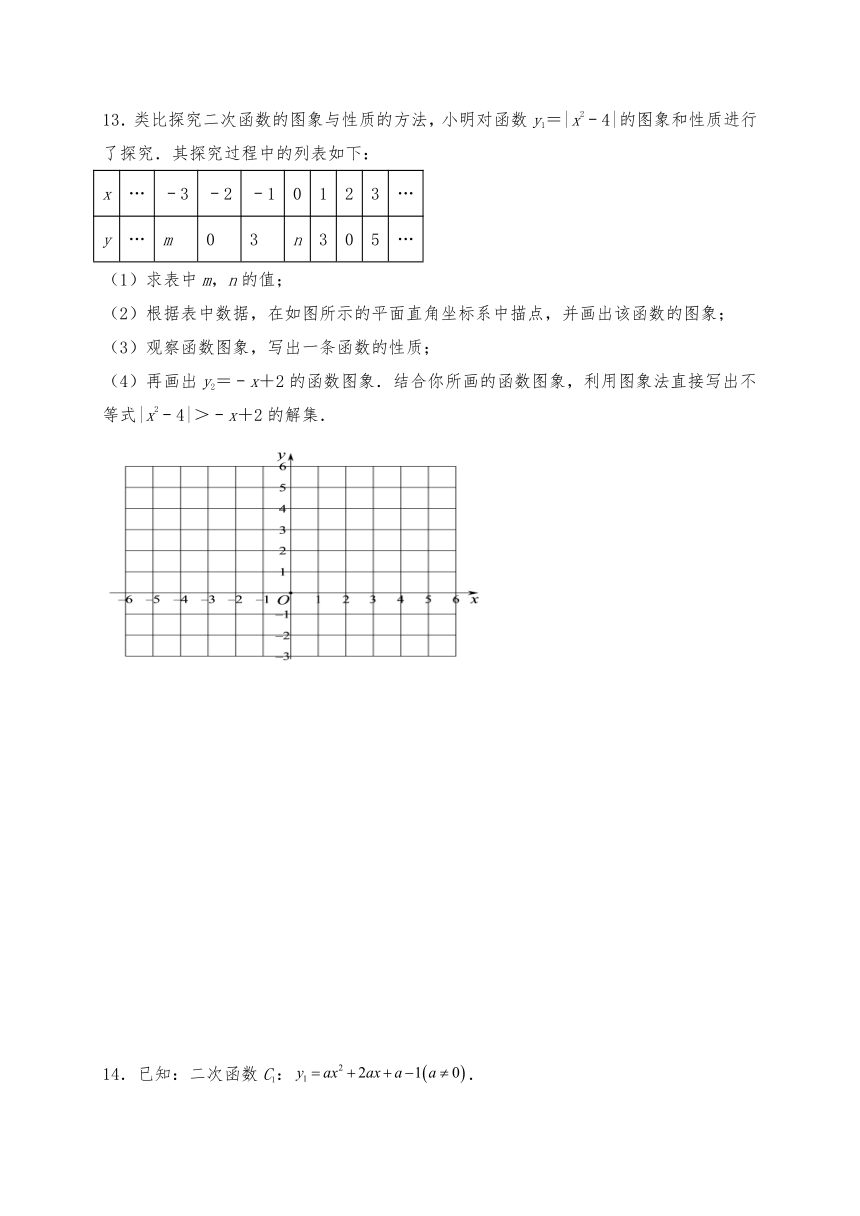
13.类比探究二次函数的图象与性质的方法,小明对函数y1=|x2﹣4|的图象和性质进行了探究.其探究过程中的列表如下:
x … ﹣3 ﹣2 ﹣1 0 1 2 3 …
y … m 0 3 n 3 0 5 …
(1)求表中m,n的值;
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出该函数的图象;
(3)观察函数图象,写出一条函数的性质;
(4)再画出y2=﹣x+2的函数图象.结合你所画的函数图象,利用图象法直接写出不等式|x2﹣4|>﹣x+2的解集.
14.已知:二次函数C1:.
(1)求二次函数C1的对称轴;
(2)已知二次函数C1的图象经过点A(-3,1).
①求a的值;
②点B在二次函数C1的图象上,点A,B关于对称轴对称,连接AB.二次函数C2:的图象,与线段AB只有一个交点,求k的取值范围.
15.合肥老城西大门有一处城门横断面分为两部分,上半部分为抛物线形状,下半部分为正方形(OMNE为正方形),己知城门宽度为4米,最高处离地面6米,如图1所示,现以O点为原点,OM所在的直线为x轴,OE所在的直线为y轴建立直角坐标系.
(1)求出上半部分抛物线的函数表达式,并写出其自变量的取值范围;
(2)有一辆宽3米,高4.5米的货车需要通过该城门进入城区,请问该货车能否正常进入?
(3)由于城门年久失修,需要搭建一个矩形“巩固门”ABCD,该“巩固门”关于抛物线对称轴对称,如图2所示,其中AB、AD、CD为三根承重钢支架,小D在抛物线上,B、C在地面上,己知钢支架每米300元,问搭建这样-一个矩形“巩固门”,仅钢支架一项,最多需要花费多少元?
答案
一、选择题。
A.A.C.C.A.D.A.D.
二、填空题。
9.﹣2
10.5
11.②③.
12..
三、解答题
13.(1)当时,,则
当时,,则
(2)根据表格中的数据,描点,连线,如图;
(3)该函数的一条性质:函数的对称轴为轴(答案不唯一);
(4)如图,
根据图图象可知当时,的取值范围为:或且
|x2﹣4|>﹣x+2的解集为或且
14.
解:(1),
对称轴:x=-1;顶点坐标(-1,-1);
(2)①∵二次函数C1经过点A(-3,1),
则,
∴a=;
②∵A(-3,1),对称轴:x=-1,
∴B(1,1).当k>0时,
当二次函数C2经过点A(-3 ,1)时,,
当二次函数C2经过点B(1,1)时,,
∴.
当k<0时,
即,
∵y2=kx2+kx(k≠0) 的图象,与线段AB只有一个交点,
∴,
解得,(舍)或.
综上所述,或.
15.
解:(1)由题意得,抛物线的顶点为(2,6),
∴设抛物线的表达式为:,
∵抛物线经过点E(0,4),
∴,
解得,
∴抛物线的表达式为:,即;
(2)由题意得,当货车走最中间时,进入的可能性最大,
即当时,,
∴该货车能正常进入;
(3)设B点的横坐标为m,AB+AD+CD的长度为L,则,
由题意知,,即,,
∴,
当,L最大,L最大=+2×1+12=13,
(元),
则最多需要花费3900元.
一、选择题。
1.如图,用绳子围成周长为10m的矩形,记矩形的一边长为,它的邻边长为,矩形的面积为.当x在一定范围内变化时,y和S都随x的变化而变化,则y与x,S与x满足的函数关系分别是( )
A.一次函数关系,二次函数关系 B.正比例函数关系,二次函数关系
C.一次函数关系,正比例函数关系 D.正比例函数关系,一次函数关系
2.对于二次函数y=﹣(x﹣1)2+4,下列说法不正确的是( )
A.当x=1时,y有最大值3
B.当x≥1时,y随x的增大而减小
C.开口向下
D.函数图象与x轴交于点(1,0)和(3,0)
3.函数y=ax+1与y=ax2+bx+1(a≠0)的图象可能是( )
A.B.
C.D.
4.已知抛物线上的部分点的横坐标与纵坐标的对应值如表:
… …
… …
以上结论正确的是( )
A.抛物线的开口向下 B.当时,随增大而增大
C.方程的根为或 D.当时,的取值范围
5.已知二次函数y=﹣(x﹣a)2+a﹣1(m为常数),则对如下两个结论的判断正确的是( )
①不论a为何值,函数图象的顶点始终在一条直线上;
②当﹣1<x<2时,y随x的增大而增大,则a的取值范围为a≥2.
A.两个都对 B.两个都错 C.①对②错 D.①错②对
6.如图, 在平面直角坐标系中放置, 点.现将 沿 轴的正方向无滑动翻转,依次得到 连续翻转 14 次, 则经过三顶点的抛物线解析式为( )
A. B.
C. D.
7.如图①,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图②,“门”的内侧曲线呈抛物线形,已知其底部宽度为80米,高度为200米.则离地面150米处的水平宽度(即CD的长)为( )
A.40米 B.30米 C.25米 D.20米
8.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E在AB边上由点A向点B运动(不与点A,点B重合),过点E作EF垂直AB交直角边于F.设AE=x,△AEF面积为y,则y关于x的函数图像大致是( )
A.B.
C.D.
二、填空题。
9.若y=(m﹣2)是关于x的二次函数,则常数m的值为_________.
10.如图,要修建一个圆形喷水池,在池中心竖直安装一根长度为水管,在水管的顶端点处安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离处达到最高,水柱落地处离池中心距离,则抛物线形水柱的最高点到地面的距离是______.
11.下表是二次函数的x,y的部分对应值:则对于该函数的性质的判断:
x … - 0 1 2 …
y … -1 - m - -1 n …
①该二次函数有最大值;②不等式y>-1的解集是x<0或x>2;③方程的两个实数根分别位于-<x<0和2<x<之间;④当x>0时,函数值y随x的增大而增大;其中正确的是__________
12.(2021·江苏东台·九年级期中)如图,直线与坐标轴交于A、B两点,点P是线段AB上的一个动点,过点P作轴的平行线交直线于点Q,△OPQ绕点O顺时针旋转45°,边PQ扫过区域(阴影部分)面积的最大值是_____________
三、解答题
13.类比探究二次函数的图象与性质的方法,小明对函数y1=|x2﹣4|的图象和性质进行了探究.其探究过程中的列表如下:
x … ﹣3 ﹣2 ﹣1 0 1 2 3 …
y … m 0 3 n 3 0 5 …
(1)求表中m,n的值;
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出该函数的图象;
(3)观察函数图象,写出一条函数的性质;
(4)再画出y2=﹣x+2的函数图象.结合你所画的函数图象,利用图象法直接写出不等式|x2﹣4|>﹣x+2的解集.
14.已知:二次函数C1:.
(1)求二次函数C1的对称轴;
(2)已知二次函数C1的图象经过点A(-3,1).
①求a的值;
②点B在二次函数C1的图象上,点A,B关于对称轴对称,连接AB.二次函数C2:的图象,与线段AB只有一个交点,求k的取值范围.
15.合肥老城西大门有一处城门横断面分为两部分,上半部分为抛物线形状,下半部分为正方形(OMNE为正方形),己知城门宽度为4米,最高处离地面6米,如图1所示,现以O点为原点,OM所在的直线为x轴,OE所在的直线为y轴建立直角坐标系.
(1)求出上半部分抛物线的函数表达式,并写出其自变量的取值范围;
(2)有一辆宽3米,高4.5米的货车需要通过该城门进入城区,请问该货车能否正常进入?
(3)由于城门年久失修,需要搭建一个矩形“巩固门”ABCD,该“巩固门”关于抛物线对称轴对称,如图2所示,其中AB、AD、CD为三根承重钢支架,小D在抛物线上,B、C在地面上,己知钢支架每米300元,问搭建这样-一个矩形“巩固门”,仅钢支架一项,最多需要花费多少元?
答案
一、选择题。
A.A.C.C.A.D.A.D.
二、填空题。
9.﹣2
10.5
11.②③.
12..
三、解答题
13.(1)当时,,则
当时,,则
(2)根据表格中的数据,描点,连线,如图;
(3)该函数的一条性质:函数的对称轴为轴(答案不唯一);
(4)如图,
根据图图象可知当时,的取值范围为:或且
|x2﹣4|>﹣x+2的解集为或且
14.
解:(1),
对称轴:x=-1;顶点坐标(-1,-1);
(2)①∵二次函数C1经过点A(-3,1),
则,
∴a=;
②∵A(-3,1),对称轴:x=-1,
∴B(1,1).当k>0时,
当二次函数C2经过点A(-3 ,1)时,,
当二次函数C2经过点B(1,1)时,,
∴.
当k<0时,
即,
∵y2=kx2+kx(k≠0) 的图象,与线段AB只有一个交点,
∴,
解得,(舍)或.
综上所述,或.
15.
解:(1)由题意得,抛物线的顶点为(2,6),
∴设抛物线的表达式为:,
∵抛物线经过点E(0,4),
∴,
解得,
∴抛物线的表达式为:,即;
(2)由题意得,当货车走最中间时,进入的可能性最大,
即当时,,
∴该货车能正常进入;
(3)设B点的横坐标为m,AB+AD+CD的长度为L,则,
由题意知,,即,,
∴,
当,L最大,L最大=+2×1+12=13,
(元),
则最多需要花费3900元.
