北师大版九年级数学下册试题 第一章 直角三角形的边角关系 单元测试卷 (含答案)
文档属性
| 名称 | 北师大版九年级数学下册试题 第一章 直角三角形的边角关系 单元测试卷 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 729.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 09:45:45 | ||
图片预览



文档简介
第一章《直角三角形的边角关系》单元测试卷
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
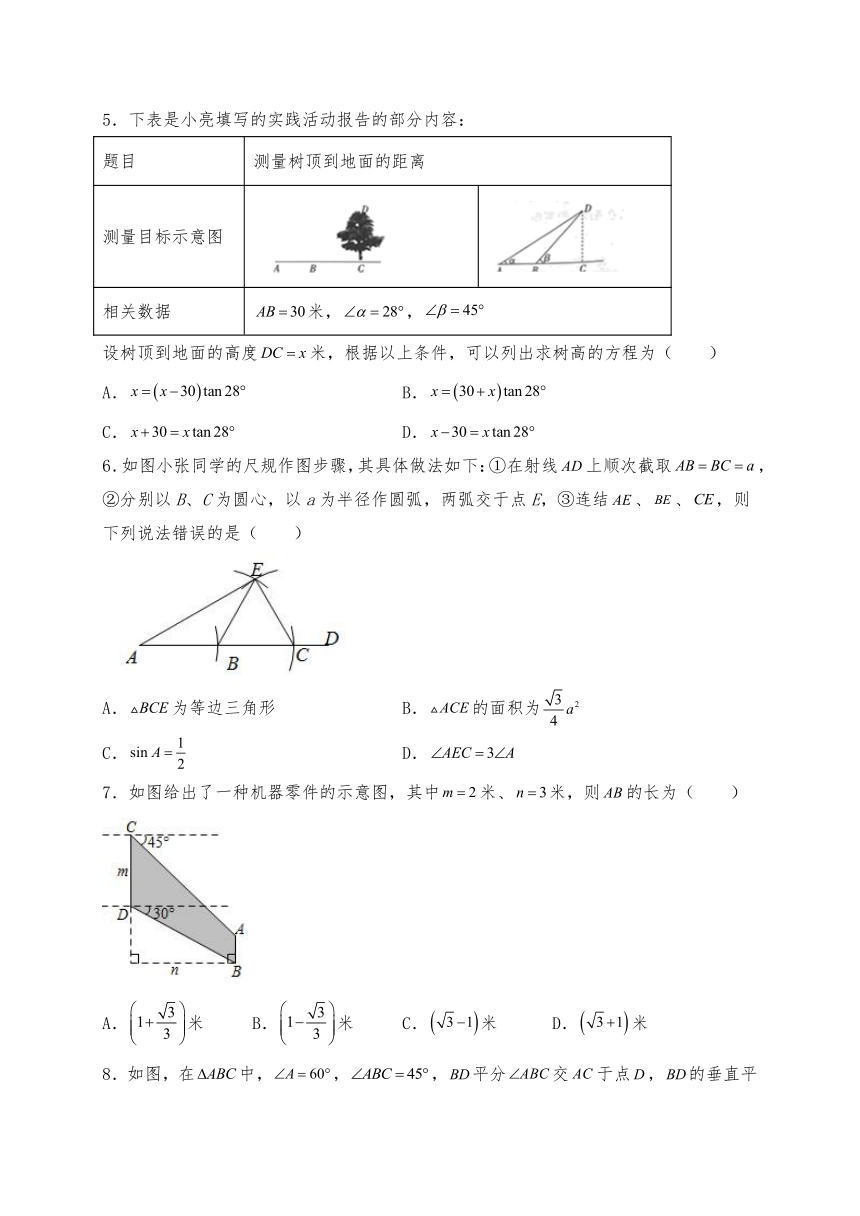
1.如图,在△ABC中,AB=AC=5,BD是AC边上的高线,DC=1,则BD的长等于( )
A.2 B.3
C.4 D.
2.如图所示,在矩形ABCD中,,,点C沿对角线BD折叠,点C的对应点为E,线段BE交AD于点F,则的值为( )
A. B. C. D.
3.如图,点A、B、C均在小正方形的顶点上,且每个小正方形的边长均为1,则的值为( )
A. B. C.1 D.
4.如果,那么=( ).
A.30° B.45° C.60° D.90°
5.下表是小亮填写的实践活动报告的部分内容:
题目 测量树顶到地面的距离
测量目标示意图
相关数据 米,,
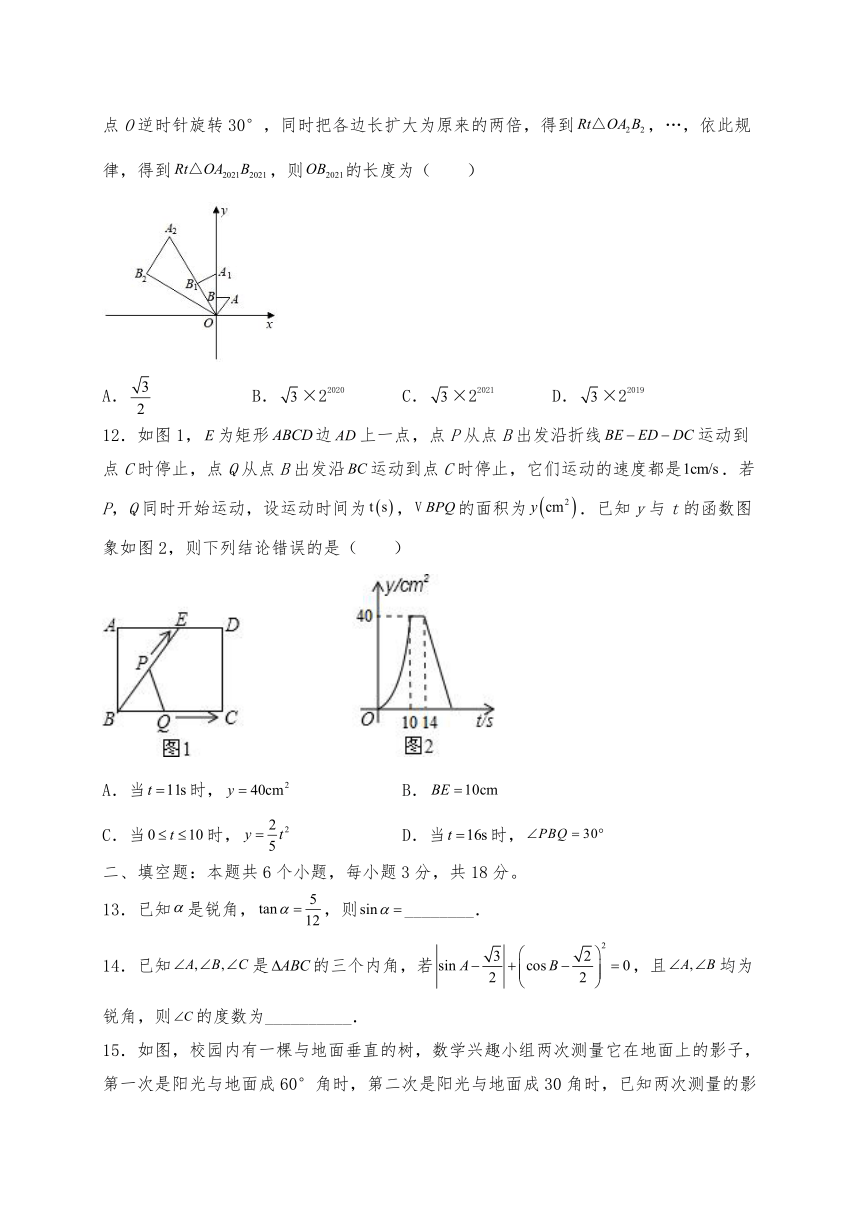
设树顶到地面的高度米,根据以上条件,可以列出求树高的方程为( )
A. B.
C. D.
6.如图小张同学的尺规作图步骤,其具体做法如下:①在射线上顺次截取,②分别以B、C为圆心,以a为半径作圆弧,两弧交于点E,③连结、、,则下列说法错误的是( )
A.为等边三角形 B.的面积为
C. D.
7.如图给出了一种机器零件的示意图,其中米、米,则的长为( )
A.米 B.米 C.米 D.米
8.如图,在中,,,平分交于点,的垂直平分线交于点,交于点,若,则的长为( )
A. B. C. D.
9.在RtABC中,∠A=90°,tan∠C=,E为AC上一点,且CE=5AE,点D为BC中点,把CDE沿ED翻折到FDE,且EG=,则DF的长度为( )
A. B. C. D.2
10.如图,已知中,,,分别为,的中点,连结,过作的平行线与的角平分线交于点,连结,若,,则的正弦值为( )
A. B. C. D.
11.如图,在平面直角坐标系中,有一个,∠ABO=90°,∠AOB=30°,直角边OB在y轴正半轴上,点A在第一象限,且OA=1,将绕原点逆时针旋转30°,同时把各边长扩大为原来的两倍(即OA1=2OA).得到,同理,将绕原点O逆时针旋转30°,同时把各边长扩大为原来的两倍,得到,…,依此规律,得到,则的长度为( )
A. B.×22020 C.×22021 D.×22019
12.如图1,为矩形边上一点,点P从点B出发沿折线运动到点C时停止,点Q从点B出发沿运动到点C时停止,它们运动的速度都是.若P,Q同时开始运动,设运动时间为,的面积为.已知y与t的函数图象如图2,则下列结论错误的是( )
A.当时, B.
C.当时, D.当时,
二、填空题:本题共6个小题,每小题3分,共18分。
13.已知是锐角,,则________.
14.已知是的三个内角,若,且均为锐角,则的度数为__________.
15.如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30角时,已知两次测量的影长相差8米,则树高AB为多少?___.(结果保留根号)
16.已知△ABC是以AB为一腰的等腰三角形,AB=5,tan∠BAC=,则△ABC的底边长为_________.
17.如图,已知菱形ABCD的对角线经过原点O,且∠B=60°,A、C分别在双曲线y=的图象上,若B在双曲线y=的图象上,则k的值为_____.
18.如图,在三角形纸片ABC中,点D是BC边的中点,连接AD,把△ABD沿着AD翻折,得到△AED,连接CE,若BC=3,tan∠ECB=,则△AEC的面积为______.
三、解答题(19题6分,其余每题8分,共46分)
19.如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=,则AD的长为多少
20.如图,在△ABC中,BC=,∠B=30°,∠C=45°,求△ABC的面积.
21.(1)通过用计算器计算,比较下列各对数的大小,并提出你的猜想:
①_______;
②_______;
③_______;
④_______;
⑤_______.
猜想:已知,则_______;
(2)如图,在中,,请根据提示,利用面积方法验证结论.
22.如图,在建筑物的左边有一个小山坡,坡底、同建筑底端在同一水平线上,斜坡的坡比为,小李从斜坡底端沿斜坡走了26米到达坡顶处,在坡顶处看建筑物的顶端D的仰角为35°,然后小李沿斜坡走了米到达底部点,已知建筑物上有一点,在处看建筑物点的仰角为18°,(点、、、、、在同一平面内)建筑物顶端到的距离长度为28.8米,(参考数据:,,,)
(1)求小李从斜坡走到处高度上升了多少米.
(2)求建筑物的高度.
23.有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度,图2是这种升降熨烫台的平面示意图,和是两根相同长度的活动支撑杆,点O是它们的连接点,,,表示熨烫台的高度.
(1)如图2,若,.
①点O到的距离为__________,的长为__________(结果保留根号);
②若,则熨烫台的高度h=__________;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度h为时,两根支撑杆的夹角是74°(如图3).求该熨烫台支撑杆的长度.
(参考数据:,,,
24.边长为4的正方形与边长为的正方形如图1摆放,将正方形绕点顺时针旋转,旋转角为,连接,.
(1)如图1,与的关系为______;
(2)如图2,连接,,判断是否为定值.若是,求这个定值;若不是,说明理由;
(3)当旋转到,,三点共线时,请直接写出此时的值.
答案
一、选择题。
B.A.B.A.B.B.C.A.D.A.B.D.
二、填空题。
13..
14.75°.
15.米
16.或8.
17.﹣9.
18..
三、解答题
19.
解:作DE⊥AB于E,如图,
∴∠AED=∠DEB=90°
∵∠C=90°,AC=BC=6,
∴,∠A=45°,
∴△ADE是等腰直角三角形,
∴AE=DE
在Rt△ADE中,设AE=x,则DE=x,
∴
在Rt△BED中,,
∴BE=5x,
∴,
∴
∴
20.
解:作AD⊥BC与D,如图,
设AD=x,
在Rt△ABD中,∵∠B=30°,
∴BD=AD=x,
在Rt△ADC中,∵∠C=45°,
∴CD=AD=x,
而BD+CD=BC,
∴x+x=,解得x=2,
即AD=2,
∴△ABC的面积=×= .
21.
(1)①=;
②=;
③=;
④=;
⑤=.
猜想:已知,则=;
(2)证明:图1中,
∵,
∴,
又∵,
∴;
图2中,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
22.
解:(1)过作,
∵的坡比,
设,
∴在中,
∴,
∴;
答:小李从斜坡走到处高度上升了10米.
(2)延长角的水平边交于则,
在中,
设,在中,,
∴
∵四边形是矩形,
∴
又∵,
在中,,
,
;
∴;
答:建筑物的高度为40.8米.
23.
解:(1)①如图2,过点O作OE⊥AC,垂足为E,
∵AO=CO=80cm,
∴∠AOE=∠AOC=×120°=60°,AC=2AE.
在Rt△AEO中,OE=OA=40(cm),
AE=AO sin∠AOE=80×=40(cm),
∴AC=2AE=80.
答:AC的长为80cm;
②延长EO交BD于F,
∵DB∥AC,
∴∠BFO=90°,∠FBO=30°,
∵OB=20cm,
∴OF=OB=×20=10(cm),
∴h=OF+OE=10+40=50,
故答案为:40,80,50;
(2)如图,过点B作BF⊥AC,垂足为F,则BF=128cm,
∵AO=CO,∠AOC=74°,
∴∠OAC=∠OCA==53°,
在Rt△ABF中,AB===160(cm),
答:支撑杆AB长160cm.
24.
(1)证明:∵四边形与为正方形,
,,
在和中,,
,
∴∠CBG=∠CDE,
∵∠CBG+∠BGC=90°,
又∵∠DGH=∠BGC,
∴∠EDC+∠DGH=90°,
∴∠DHG=180° 90°=90°,
∴BG⊥DE.
(2)解:连接,,设,交于点,,交于点,
,,,
在和中,,.
,,
,
,由勾股定理得,,
,
,,,,
.
(3)①分类讨论,情况一,如下所示:
作于点,
为等腰直角三角形,
,且,
在中,,
,
,
.
.
②分类讨论,情况二,如下所示:
作于点,
为等腰直角三角形,
,且,
在中,,
,
,
,
,
.
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如图,在△ABC中,AB=AC=5,BD是AC边上的高线,DC=1,则BD的长等于( )
A.2 B.3
C.4 D.
2.如图所示,在矩形ABCD中,,,点C沿对角线BD折叠,点C的对应点为E,线段BE交AD于点F,则的值为( )
A. B. C. D.
3.如图,点A、B、C均在小正方形的顶点上,且每个小正方形的边长均为1,则的值为( )
A. B. C.1 D.
4.如果,那么=( ).
A.30° B.45° C.60° D.90°
5.下表是小亮填写的实践活动报告的部分内容:
题目 测量树顶到地面的距离
测量目标示意图
相关数据 米,,
设树顶到地面的高度米,根据以上条件,可以列出求树高的方程为( )
A. B.
C. D.
6.如图小张同学的尺规作图步骤,其具体做法如下:①在射线上顺次截取,②分别以B、C为圆心,以a为半径作圆弧,两弧交于点E,③连结、、,则下列说法错误的是( )
A.为等边三角形 B.的面积为
C. D.
7.如图给出了一种机器零件的示意图,其中米、米,则的长为( )
A.米 B.米 C.米 D.米
8.如图,在中,,,平分交于点,的垂直平分线交于点,交于点,若,则的长为( )
A. B. C. D.
9.在RtABC中,∠A=90°,tan∠C=,E为AC上一点,且CE=5AE,点D为BC中点,把CDE沿ED翻折到FDE,且EG=,则DF的长度为( )
A. B. C. D.2
10.如图,已知中,,,分别为,的中点,连结,过作的平行线与的角平分线交于点,连结,若,,则的正弦值为( )
A. B. C. D.
11.如图,在平面直角坐标系中,有一个,∠ABO=90°,∠AOB=30°,直角边OB在y轴正半轴上,点A在第一象限,且OA=1,将绕原点逆时针旋转30°,同时把各边长扩大为原来的两倍(即OA1=2OA).得到,同理,将绕原点O逆时针旋转30°,同时把各边长扩大为原来的两倍,得到,…,依此规律,得到,则的长度为( )
A. B.×22020 C.×22021 D.×22019
12.如图1,为矩形边上一点,点P从点B出发沿折线运动到点C时停止,点Q从点B出发沿运动到点C时停止,它们运动的速度都是.若P,Q同时开始运动,设运动时间为,的面积为.已知y与t的函数图象如图2,则下列结论错误的是( )
A.当时, B.
C.当时, D.当时,
二、填空题:本题共6个小题,每小题3分,共18分。
13.已知是锐角,,则________.
14.已知是的三个内角,若,且均为锐角,则的度数为__________.
15.如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30角时,已知两次测量的影长相差8米,则树高AB为多少?___.(结果保留根号)
16.已知△ABC是以AB为一腰的等腰三角形,AB=5,tan∠BAC=,则△ABC的底边长为_________.
17.如图,已知菱形ABCD的对角线经过原点O,且∠B=60°,A、C分别在双曲线y=的图象上,若B在双曲线y=的图象上,则k的值为_____.
18.如图,在三角形纸片ABC中,点D是BC边的中点,连接AD,把△ABD沿着AD翻折,得到△AED,连接CE,若BC=3,tan∠ECB=,则△AEC的面积为______.
三、解答题(19题6分,其余每题8分,共46分)
19.如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=,则AD的长为多少
20.如图,在△ABC中,BC=,∠B=30°,∠C=45°,求△ABC的面积.
21.(1)通过用计算器计算,比较下列各对数的大小,并提出你的猜想:
①_______;
②_______;
③_______;
④_______;
⑤_______.
猜想:已知,则_______;
(2)如图,在中,,请根据提示,利用面积方法验证结论.
22.如图,在建筑物的左边有一个小山坡,坡底、同建筑底端在同一水平线上,斜坡的坡比为,小李从斜坡底端沿斜坡走了26米到达坡顶处,在坡顶处看建筑物的顶端D的仰角为35°,然后小李沿斜坡走了米到达底部点,已知建筑物上有一点,在处看建筑物点的仰角为18°,(点、、、、、在同一平面内)建筑物顶端到的距离长度为28.8米,(参考数据:,,,)
(1)求小李从斜坡走到处高度上升了多少米.
(2)求建筑物的高度.
23.有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度,图2是这种升降熨烫台的平面示意图,和是两根相同长度的活动支撑杆,点O是它们的连接点,,,表示熨烫台的高度.
(1)如图2,若,.
①点O到的距离为__________,的长为__________(结果保留根号);
②若,则熨烫台的高度h=__________;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度h为时,两根支撑杆的夹角是74°(如图3).求该熨烫台支撑杆的长度.
(参考数据:,,,
24.边长为4的正方形与边长为的正方形如图1摆放,将正方形绕点顺时针旋转,旋转角为,连接,.
(1)如图1,与的关系为______;
(2)如图2,连接,,判断是否为定值.若是,求这个定值;若不是,说明理由;
(3)当旋转到,,三点共线时,请直接写出此时的值.
答案
一、选择题。
B.A.B.A.B.B.C.A.D.A.B.D.
二、填空题。
13..
14.75°.
15.米
16.或8.
17.﹣9.
18..
三、解答题
19.
解:作DE⊥AB于E,如图,
∴∠AED=∠DEB=90°
∵∠C=90°,AC=BC=6,
∴,∠A=45°,
∴△ADE是等腰直角三角形,
∴AE=DE
在Rt△ADE中,设AE=x,则DE=x,
∴
在Rt△BED中,,
∴BE=5x,
∴,
∴
∴
20.
解:作AD⊥BC与D,如图,
设AD=x,
在Rt△ABD中,∵∠B=30°,
∴BD=AD=x,
在Rt△ADC中,∵∠C=45°,
∴CD=AD=x,
而BD+CD=BC,
∴x+x=,解得x=2,
即AD=2,
∴△ABC的面积=×= .
21.
(1)①=;
②=;
③=;
④=;
⑤=.
猜想:已知,则=;
(2)证明:图1中,
∵,
∴,
又∵,
∴;
图2中,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
22.
解:(1)过作,
∵的坡比,
设,
∴在中,
∴,
∴;
答:小李从斜坡走到处高度上升了10米.
(2)延长角的水平边交于则,
在中,
设,在中,,
∴
∵四边形是矩形,
∴
又∵,
在中,,
,
;
∴;
答:建筑物的高度为40.8米.
23.
解:(1)①如图2,过点O作OE⊥AC,垂足为E,
∵AO=CO=80cm,
∴∠AOE=∠AOC=×120°=60°,AC=2AE.
在Rt△AEO中,OE=OA=40(cm),
AE=AO sin∠AOE=80×=40(cm),
∴AC=2AE=80.
答:AC的长为80cm;
②延长EO交BD于F,
∵DB∥AC,
∴∠BFO=90°,∠FBO=30°,
∵OB=20cm,
∴OF=OB=×20=10(cm),
∴h=OF+OE=10+40=50,
故答案为:40,80,50;
(2)如图,过点B作BF⊥AC,垂足为F,则BF=128cm,
∵AO=CO,∠AOC=74°,
∴∠OAC=∠OCA==53°,
在Rt△ABF中,AB===160(cm),
答:支撑杆AB长160cm.
24.
(1)证明:∵四边形与为正方形,
,,
在和中,,
,
∴∠CBG=∠CDE,
∵∠CBG+∠BGC=90°,
又∵∠DGH=∠BGC,
∴∠EDC+∠DGH=90°,
∴∠DHG=180° 90°=90°,
∴BG⊥DE.
(2)解:连接,,设,交于点,,交于点,
,,,
在和中,,.
,,
,
,由勾股定理得,,
,
,,,,
.
(3)①分类讨论,情况一,如下所示:
作于点,
为等腰直角三角形,
,且,
在中,,
,
,
.
.
②分类讨论,情况二,如下所示:
作于点,
为等腰直角三角形,
,且,
在中,,
,
,
,
,
.
