北师大版九年级数学下册试题 第一章 直角三角形的边角关系 复习卷 (含答案)
文档属性
| 名称 | 北师大版九年级数学下册试题 第一章 直角三角形的边角关系 复习卷 (含答案) | 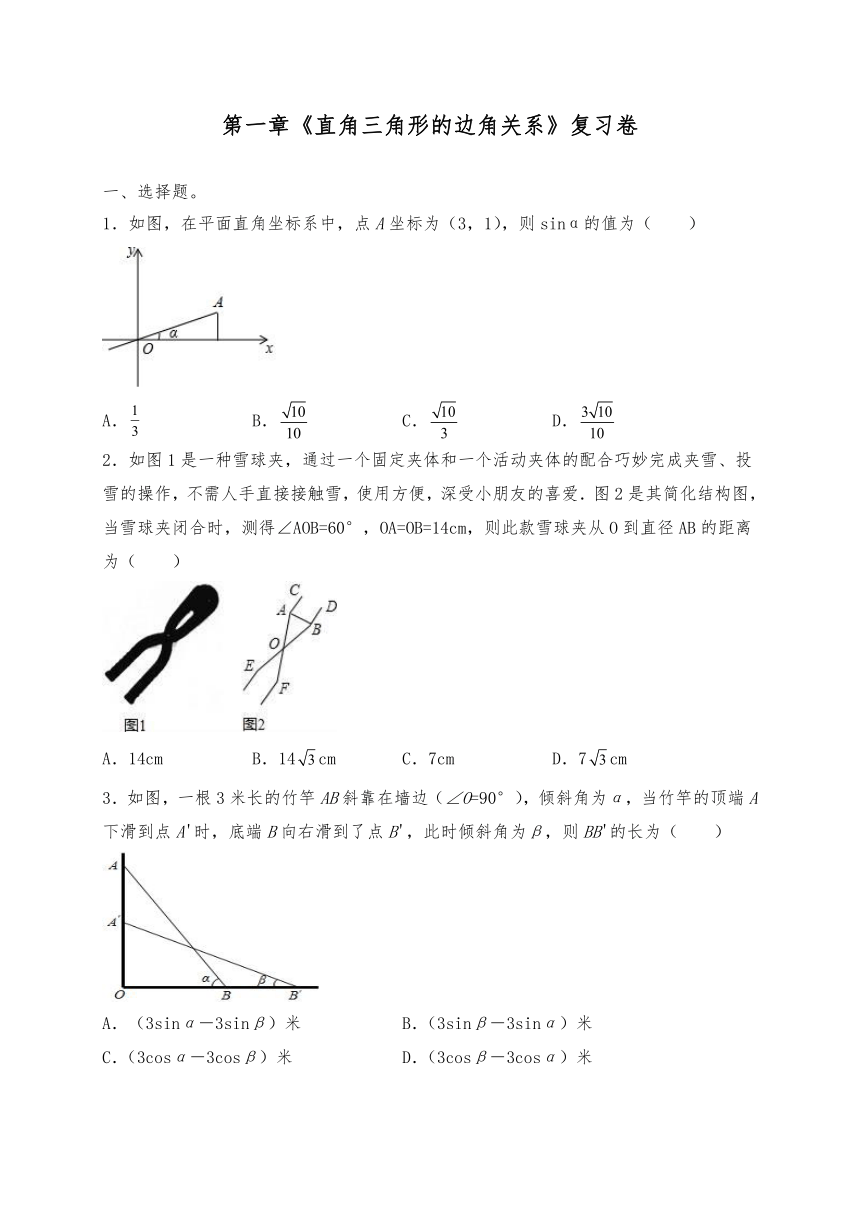 | |
| 格式 | zip | ||
| 文件大小 | 260.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 09:46:29 | ||
图片预览


文档简介
第一章《直角三角形的边角关系》复习卷
一、选择题。
1.如图,在平面直角坐标系中,点A坐标为(3,1),则sinα的值为( )
A. B. C. D.
2.如图1是一种雪球夹,通过一个固定夹体和一个活动夹体的配合巧妙完成夹雪、投雪的操作,不需人手直接接触雪,使用方便,深受小朋友的喜爱.图2是其简化结构图,当雪球夹闭合时,测得∠AOB=60°,OA=OB=14cm,则此款雪球夹从O到直径AB的距离为( )
A.14cm B.14cm C.7cm D.7cm
3.如图,一根3米长的竹竿AB斜靠在墙边(∠O=90°),倾斜角为α,当竹竿的顶端A下滑到点A'时,底端B向右滑到了点B',此时倾斜角为β,则BB'的长为( )
(3sinα-3sinβ)米 B.(3sinβ-3sinα)米
C.(3cosα-3cosβ)米 D.(3cosβ-3cosα)米
4.如图,正方形ABCD中,对角线AC、BD交于点O,点M、N分别为OB、OC的中点,则sin∠OMN的值为( )
A. B.1 C. D.
5.如图,四个全等的直角三角形纸片既可以拼成(内角不是直角)的菱形,也可以拼成正方形,则菱形面积和正方形面积之比为( )
A.1 B. C. D.
6.如图,小敏在参观大风车时,想测一下风叶AB的长度.她首先通过C处的铭牌简介得知每个风车杆子BC的高度为98米,然后沿水平方向走到D处,再沿着斜坡DE走了35米到达E处,她站在E处当风叶AB转到铅垂方向时测得点A的仰角为68°;当风叶AB转到水平方向A′B时测得点A′的仰角为45°,若斜坡DE的坡度i=1:0.75,则风叶AB的长度约为( )米.(参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50)
A.25 B.30 C.32 D.35
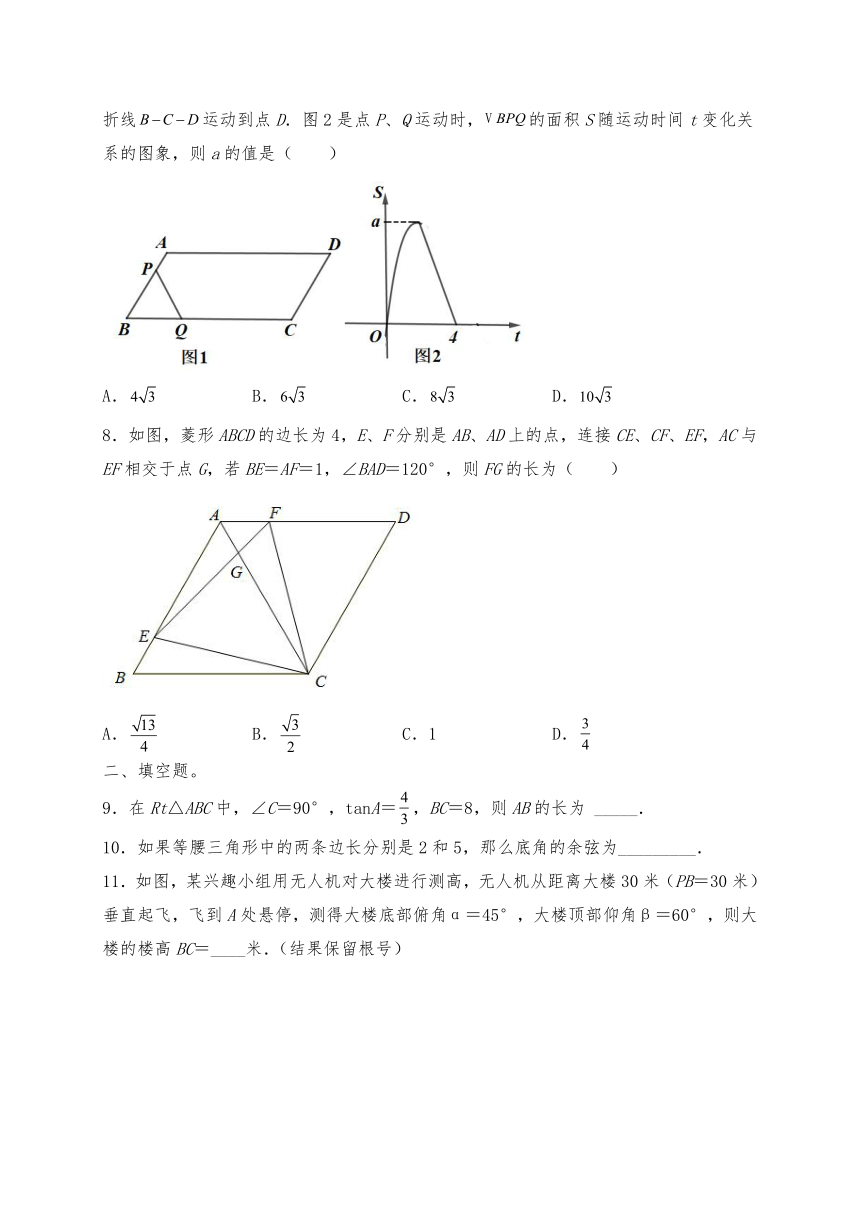
7.如图1,在平行四边形中,,;动点P以每秒1个单位的速度从点A出发沿线段运动到点B,同时动点Q以每秒4个单位的速度从点B出发,沿折线运动到点D.图2是点P、Q运动时,的面积S随运动时间t变化关系的图象,则a的值是( )
A. B. C. D.
8.如图,菱形ABCD的边长为4,E、F分别是AB、AD上的点,连接CE、CF、EF,AC与EF相交于点G,若BE=AF=1,∠BAD=120°,则FG的长为( )
A. B. C.1 D.
二、填空题。
9.在Rt△ABC中,∠C=90°,tanA=,BC=8,则AB的长为 _____.
10.如果等腰三角形中的两条边长分别是2和5,那么底角的余弦为_________.
11.如图,某兴趣小组用无人机对大楼进行测高,无人机从距离大楼30米(PB=30米)垂直起飞,飞到A处悬停,测得大楼底部俯角α=45°,大楼顶部仰角β=60°,则大楼的楼高BC=____米.(结果保留根号)
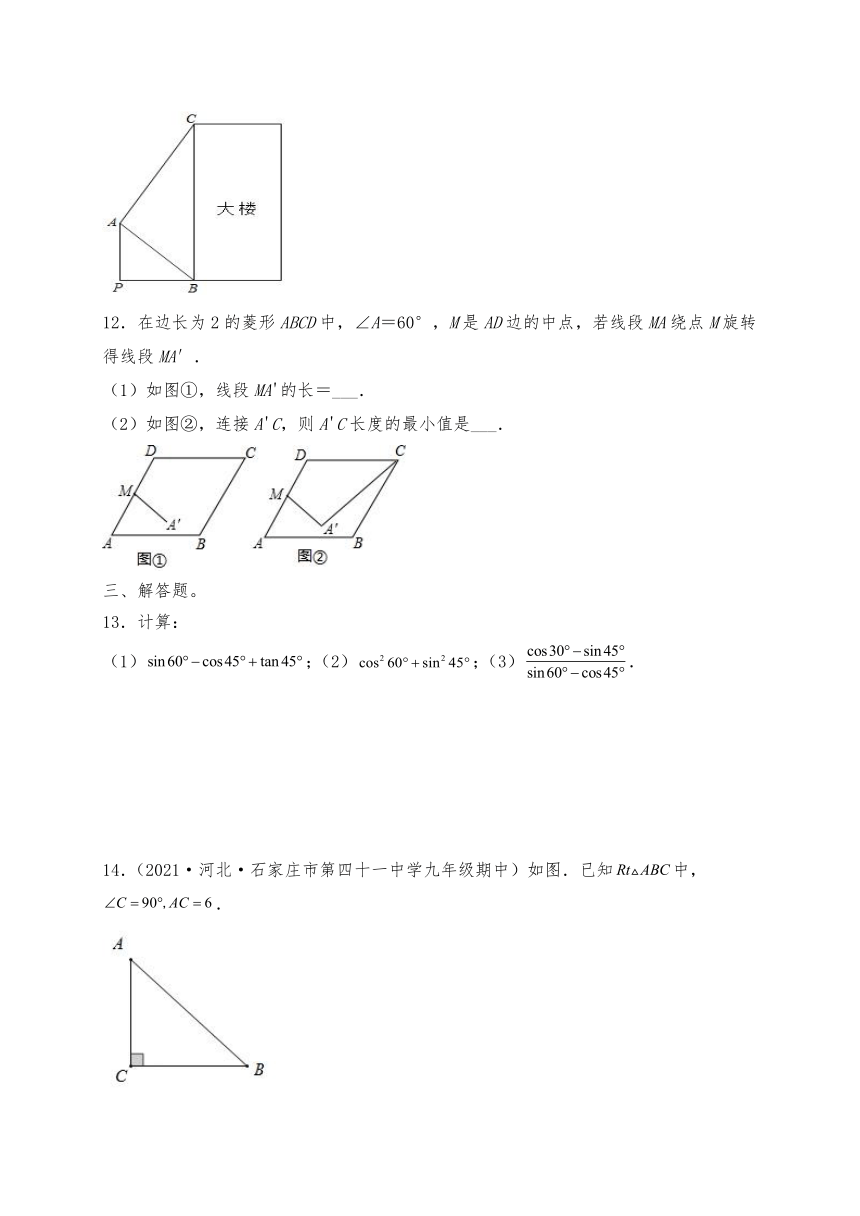
12.在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,若线段MA绕点M旋转得线段MA′.
(1)如图①,线段MA'的长=___.
(2)如图②,连接A'C,则A'C长度的最小值是___.
三、解答题。
13.计算:
(1);(2);(3).
14.(2021·河北·石家庄市第四十一中学九年级期中)如图.已知中,.
(1)若,求的长度.
(2)若,求的长度.
15.图1是一台实物投影仪,图2是它的示意图,折线B﹣A﹣O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8cm,CD=8cm,AB=30cm,BC=35cm.(结果精确到0.1).
(1)如图2,∠ABC=70°,BCOE.
①填空:∠BAO=_______°.
②求投影探头的端点D到桌面OE的距离.
(2)如图3,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6cm时,求∠ABC的大小.(参考数据:sin70°≈0.94,cos20°≈0.94,sin36.8°≈0.60,cos53.2°≈0.60)
答案
一、选择题。
B.D.D.C.C.B.A.A .
二、填空题。
9.10.
10.
11..
12.1.
三、解答题。
13.
(1)原式=;
(2)原式=;
(3)原式=.
14.(1)中,,,
(2)在中
,
设,
勾股定理可得
15.解:(1)①过点A作AGBC,如图1,则∠BAG=∠ABC=70°,
∵BCOE,
∴AGOE,
∴∠GAO=∠AOE=90°,
∴∠BAO=90°+70°=160°,
故答案为:160;
②过点A作AF⊥BC于点F,如图2,
则AF=AB sin∠ABF=30×sin70°≈28.2(cm),
∴投影探头的端点D到桌面OE的距离为:AF+OA﹣CD=28.2+6.8﹣8=27.0(cm);
(2)作DH⊥OE于点H,过点B作BM⊥CD,与DC延长线相交于点M,过A作AF⊥BM于点F,如图3,
则∠MBA=70°,AF=28.2cm,DH=6cm,BC=35cm,CD=8cm,
∴CM=AF+AO﹣DH﹣CD=28.2+6.8﹣6﹣8=21(cm),
∴sin∠MBC=,
∴∠MBC=36.8°,
∴∠ABC=∠ABM﹣∠MBC=33.2°.
一、选择题。
1.如图,在平面直角坐标系中,点A坐标为(3,1),则sinα的值为( )
A. B. C. D.
2.如图1是一种雪球夹,通过一个固定夹体和一个活动夹体的配合巧妙完成夹雪、投雪的操作,不需人手直接接触雪,使用方便,深受小朋友的喜爱.图2是其简化结构图,当雪球夹闭合时,测得∠AOB=60°,OA=OB=14cm,则此款雪球夹从O到直径AB的距离为( )
A.14cm B.14cm C.7cm D.7cm
3.如图,一根3米长的竹竿AB斜靠在墙边(∠O=90°),倾斜角为α,当竹竿的顶端A下滑到点A'时,底端B向右滑到了点B',此时倾斜角为β,则BB'的长为( )
(3sinα-3sinβ)米 B.(3sinβ-3sinα)米
C.(3cosα-3cosβ)米 D.(3cosβ-3cosα)米
4.如图,正方形ABCD中,对角线AC、BD交于点O,点M、N分别为OB、OC的中点,则sin∠OMN的值为( )
A. B.1 C. D.
5.如图,四个全等的直角三角形纸片既可以拼成(内角不是直角)的菱形,也可以拼成正方形,则菱形面积和正方形面积之比为( )
A.1 B. C. D.
6.如图,小敏在参观大风车时,想测一下风叶AB的长度.她首先通过C处的铭牌简介得知每个风车杆子BC的高度为98米,然后沿水平方向走到D处,再沿着斜坡DE走了35米到达E处,她站在E处当风叶AB转到铅垂方向时测得点A的仰角为68°;当风叶AB转到水平方向A′B时测得点A′的仰角为45°,若斜坡DE的坡度i=1:0.75,则风叶AB的长度约为( )米.(参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50)
A.25 B.30 C.32 D.35
7.如图1,在平行四边形中,,;动点P以每秒1个单位的速度从点A出发沿线段运动到点B,同时动点Q以每秒4个单位的速度从点B出发,沿折线运动到点D.图2是点P、Q运动时,的面积S随运动时间t变化关系的图象,则a的值是( )
A. B. C. D.
8.如图,菱形ABCD的边长为4,E、F分别是AB、AD上的点,连接CE、CF、EF,AC与EF相交于点G,若BE=AF=1,∠BAD=120°,则FG的长为( )
A. B. C.1 D.
二、填空题。
9.在Rt△ABC中,∠C=90°,tanA=,BC=8,则AB的长为 _____.
10.如果等腰三角形中的两条边长分别是2和5,那么底角的余弦为_________.
11.如图,某兴趣小组用无人机对大楼进行测高,无人机从距离大楼30米(PB=30米)垂直起飞,飞到A处悬停,测得大楼底部俯角α=45°,大楼顶部仰角β=60°,则大楼的楼高BC=____米.(结果保留根号)
12.在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,若线段MA绕点M旋转得线段MA′.
(1)如图①,线段MA'的长=___.
(2)如图②,连接A'C,则A'C长度的最小值是___.
三、解答题。
13.计算:
(1);(2);(3).
14.(2021·河北·石家庄市第四十一中学九年级期中)如图.已知中,.
(1)若,求的长度.
(2)若,求的长度.
15.图1是一台实物投影仪,图2是它的示意图,折线B﹣A﹣O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8cm,CD=8cm,AB=30cm,BC=35cm.(结果精确到0.1).
(1)如图2,∠ABC=70°,BCOE.
①填空:∠BAO=_______°.
②求投影探头的端点D到桌面OE的距离.
(2)如图3,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6cm时,求∠ABC的大小.(参考数据:sin70°≈0.94,cos20°≈0.94,sin36.8°≈0.60,cos53.2°≈0.60)
答案
一、选择题。
B.D.D.C.C.B.A.A .
二、填空题。
9.10.
10.
11..
12.1.
三、解答题。
13.
(1)原式=;
(2)原式=;
(3)原式=.
14.(1)中,,,
(2)在中
,
设,
勾股定理可得
15.解:(1)①过点A作AGBC,如图1,则∠BAG=∠ABC=70°,
∵BCOE,
∴AGOE,
∴∠GAO=∠AOE=90°,
∴∠BAO=90°+70°=160°,
故答案为:160;
②过点A作AF⊥BC于点F,如图2,
则AF=AB sin∠ABF=30×sin70°≈28.2(cm),
∴投影探头的端点D到桌面OE的距离为:AF+OA﹣CD=28.2+6.8﹣8=27.0(cm);
(2)作DH⊥OE于点H,过点B作BM⊥CD,与DC延长线相交于点M,过A作AF⊥BM于点F,如图3,
则∠MBA=70°,AF=28.2cm,DH=6cm,BC=35cm,CD=8cm,
∴CM=AF+AO﹣DH﹣CD=28.2+6.8﹣6﹣8=21(cm),
∴sin∠MBC=,
∴∠MBC=36.8°,
∴∠ABC=∠ABM﹣∠MBC=33.2°.
