北师大版数学九年级下册 第三章 圆 专题四 模型拓展——圆中经典模型(隐圆问题)课件(共25张PPT)
文档属性
| 名称 | 北师大版数学九年级下册 第三章 圆 专题四 模型拓展——圆中经典模型(隐圆问题)课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 13:31:18 | ||
图片预览



文档简介
(共25张PPT)
专题四 模型拓展——圆中经典模型(隐圆问题)
第三章 圆
目录
01
模型解读
02
针对训练
模型一 定弦定角模型
模型解读
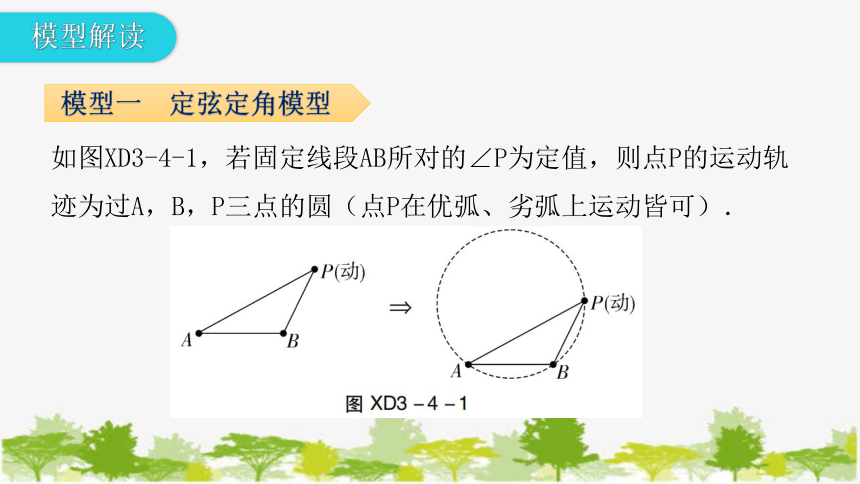
如图XD3-4-1,若固定线段AB所对的∠P为定值,则点P的运动轨迹为过A,B,P三点的圆(点P在优弧、劣弧上运动皆可).
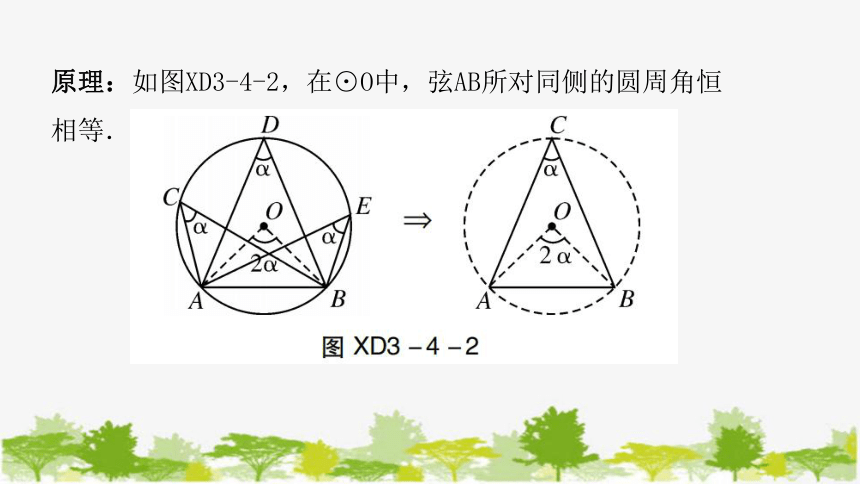
原理:如图XD3-4-2,在⊙O中,弦AB所对同侧的圆周角恒
相等.
针对训练
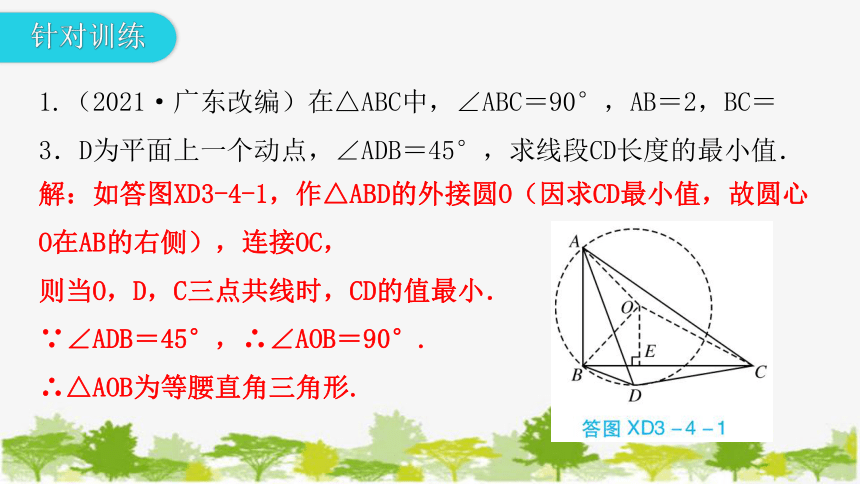
1.(2021·广东改编)在△ABC中,∠ABC=90°,AB=2,BC=3.D为平面上一个动点,∠ADB=45°,求线段CD长度的最小值.
解:如答图XD3-4-1,作△ABD的外接圆O(因求CD最小值,故圆心O在AB的右侧),连接OC,
则当O,D,C三点共线时,CD的值最小.
∵∠ADB=45°,∴∠AOB=90°.
∴△AOB为等腰直角三角形.
模型解读
模型二 动点定长模型
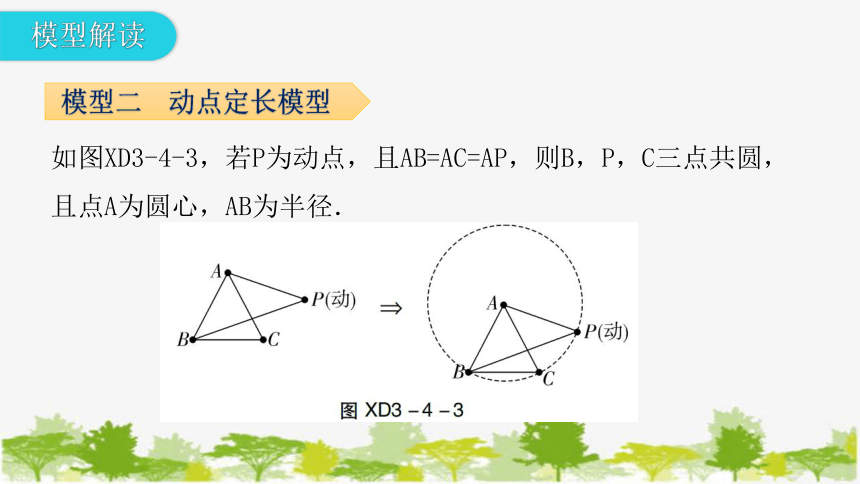
如图XD3-4-3,若P为动点,且AB=AC=AP,则B,P,C三点共圆,且点A为圆心,AB为半径.
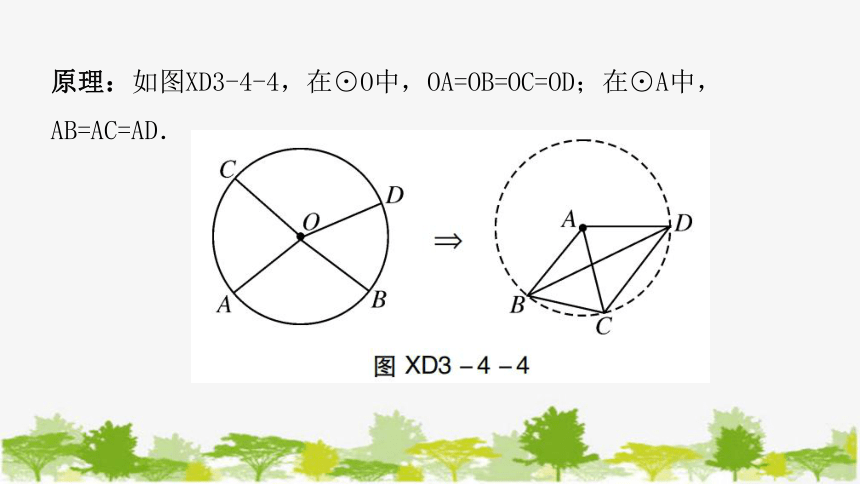
原理:如图XD3-4-4,在⊙O中,OA=OB=OC=OD;在⊙A中,AB=AC=AD.
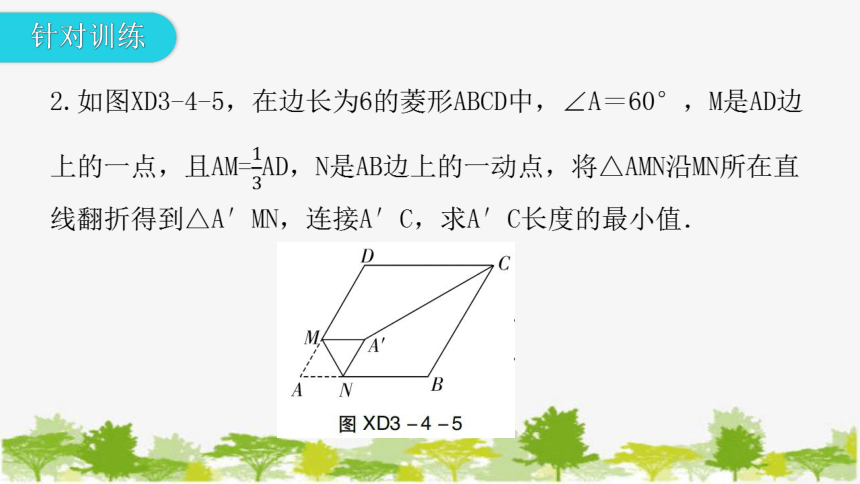
针对训练
模型解读
模型三 直角圆周模型
如图XD3-4-6,若固定线段AB所对动∠C恒为90°,则A,B,C三点共圆,且AB为直径.
原理:如图XD3-4-7,在⊙中,若AB是直径,C是圆上的一点,则∠ACB=90°.
针对训练
3. 如图XD3-4-8,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB+∠PBA=90°,求线段CP长的最小值.
模型解读
模型四 四点共圆模型
【模型一】
如图XD3-4-9,若动角∠A+动角∠C=180°,则A,B,C,D四点共圆.
原理:如图XD3-4-10,四边形ABCD是⊙O的内接四边形,则∠1+∠2=180°,∠3+∠4=180°.
针对训练
4.如图XD3-4-11,在等边△ABC中,AB=6,P为AB上一动点,PD⊥BC,PE⊥AC,求DE的最小值.
解:如答图XD3-4-4,连接PC,取CP的中点O,连接OE,OD,过点O作OH⊥DE于点H.
∵△ABC是等边三角形,
∴∠ACB=∠B=60°,BC=AC=AB=6.
∵PD⊥BC,PE⊥AC,
∴∠PDC=∠PEC=90°.
∴∠PDC+∠PEC=180°.
∴C,D,P,E四点共圆.
∴∠EOD=2∠ACB=120°.
∴当OE的值最小时,DE的值最小.
∴当CP⊥AB时,OE的值最小,即DE的值最小.
模型解读
【模型二】
如图XD3-4-12,若固定线段AB所对同侧动角∠P=∠C,则A,B,C,P四点共圆.
原理:如图XD3-4-13,在⊙O中,四边形ABCD是⊙O的内接四边形,则∠1=∠2,∠3=∠4.
针对训练
5.如图XD3-4-14,PA,PB切⊙O于A,B两点,过点P作割线交⊙O于点C,D,过点B作BE∥CD,连接AE交PD于点M.求证:M为DC的
中点.
谢 谢
专题四 模型拓展——圆中经典模型(隐圆问题)
第三章 圆
目录
01
模型解读
02
针对训练
模型一 定弦定角模型
模型解读
如图XD3-4-1,若固定线段AB所对的∠P为定值,则点P的运动轨迹为过A,B,P三点的圆(点P在优弧、劣弧上运动皆可).
原理:如图XD3-4-2,在⊙O中,弦AB所对同侧的圆周角恒
相等.
针对训练
1.(2021·广东改编)在△ABC中,∠ABC=90°,AB=2,BC=3.D为平面上一个动点,∠ADB=45°,求线段CD长度的最小值.
解:如答图XD3-4-1,作△ABD的外接圆O(因求CD最小值,故圆心O在AB的右侧),连接OC,
则当O,D,C三点共线时,CD的值最小.
∵∠ADB=45°,∴∠AOB=90°.
∴△AOB为等腰直角三角形.
模型解读
模型二 动点定长模型
如图XD3-4-3,若P为动点,且AB=AC=AP,则B,P,C三点共圆,且点A为圆心,AB为半径.
原理:如图XD3-4-4,在⊙O中,OA=OB=OC=OD;在⊙A中,AB=AC=AD.
针对训练
模型解读
模型三 直角圆周模型
如图XD3-4-6,若固定线段AB所对动∠C恒为90°,则A,B,C三点共圆,且AB为直径.
原理:如图XD3-4-7,在⊙中,若AB是直径,C是圆上的一点,则∠ACB=90°.
针对训练
3. 如图XD3-4-8,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB+∠PBA=90°,求线段CP长的最小值.
模型解读
模型四 四点共圆模型
【模型一】
如图XD3-4-9,若动角∠A+动角∠C=180°,则A,B,C,D四点共圆.
原理:如图XD3-4-10,四边形ABCD是⊙O的内接四边形,则∠1+∠2=180°,∠3+∠4=180°.
针对训练
4.如图XD3-4-11,在等边△ABC中,AB=6,P为AB上一动点,PD⊥BC,PE⊥AC,求DE的最小值.
解:如答图XD3-4-4,连接PC,取CP的中点O,连接OE,OD,过点O作OH⊥DE于点H.
∵△ABC是等边三角形,
∴∠ACB=∠B=60°,BC=AC=AB=6.
∵PD⊥BC,PE⊥AC,
∴∠PDC=∠PEC=90°.
∴∠PDC+∠PEC=180°.
∴C,D,P,E四点共圆.
∴∠EOD=2∠ACB=120°.
∴当OE的值最小时,DE的值最小.
∴当CP⊥AB时,OE的值最小,即DE的值最小.
模型解读
【模型二】
如图XD3-4-12,若固定线段AB所对同侧动角∠P=∠C,则A,B,C,P四点共圆.
原理:如图XD3-4-13,在⊙O中,四边形ABCD是⊙O的内接四边形,则∠1=∠2,∠3=∠4.
针对训练
5.如图XD3-4-14,PA,PB切⊙O于A,B两点,过点P作割线交⊙O于点C,D,过点B作BE∥CD,连接AE交PD于点M.求证:M为DC的
中点.
谢 谢
