抓基础、重计算、提素养 课件(38张PPT)
文档属性
| 名称 | 抓基础、重计算、提素养 课件(38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 15:04:46 | ||
图片预览







文档简介
(共38张PPT)
抓基础、重计算、提素养
选择性必修第一册第二章第三章解析几何
3.解析几何在高考中的地位
4.教学建议
试题分析,说解题思路
1.备课组计划和有特色教学措施
2.新旧教材解析几何内容解读
备课组计划和有特色措施
01
备课组计划
依据统一安排,本学期主要完成解析几何、数列、统计的相关内容教学,目前没有增加其他内容的打算,因为本学期的内容相对难度较大,因而需要更多的课时来加强学生的学习与理解。
备课组措施
依照学生学习的实际,结合课标的基本理念,每个内容的教学,也要遵循着螺旋上升的意识,重视复习总结与提升的安排。
在具体的教学中,采用集体备课形式,以组内专家型教师为引领,发挥各位教师的主观能动性,备好每一堂课。备课组针对本年级学生的实际情况,充分利用并完善上届备课组自编的一课一练习题,习题配置难度、题量适中,重点关注数学本质的深度挖掘。
新旧教材解析几何内容解读
02
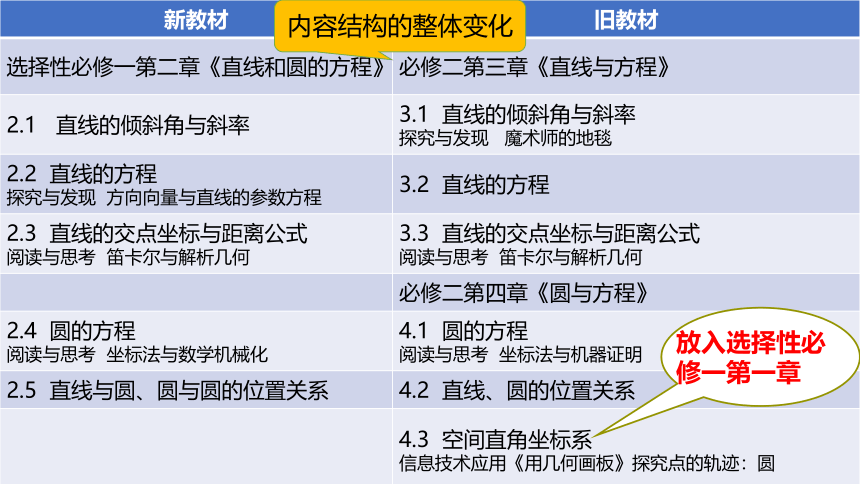
新教材 旧教材
选择性必修一第二章《直线和圆的方程》 必修二第三章《直线与方程》
2.1 直线的倾斜角与斜率 3.1 直线的倾斜角与斜率
探究与发现 魔术师的地毯
2.2 直线的方程 探究与发现 方向向量与直线的参数方程 3.2 直线的方程
2.3 直线的交点坐标与距离公式 阅读与思考 笛卡尔与解析几何 3.3 直线的交点坐标与距离公式
阅读与思考 笛卡尔与解析几何
必修二第四章《圆与方程》
2.4 圆的方程 阅读与思考 坐标法与数学机械化 4.1 圆的方程
阅读与思考 坐标法与机器证明
2.5 直线与圆、圆与圆的位置关系 4.2 直线、圆的位置关系
4.3 空间直角坐标系
信息技术应用《用几何画板》探究点的轨迹:圆
放入选择性必修一第一章
内容结构的整体变化
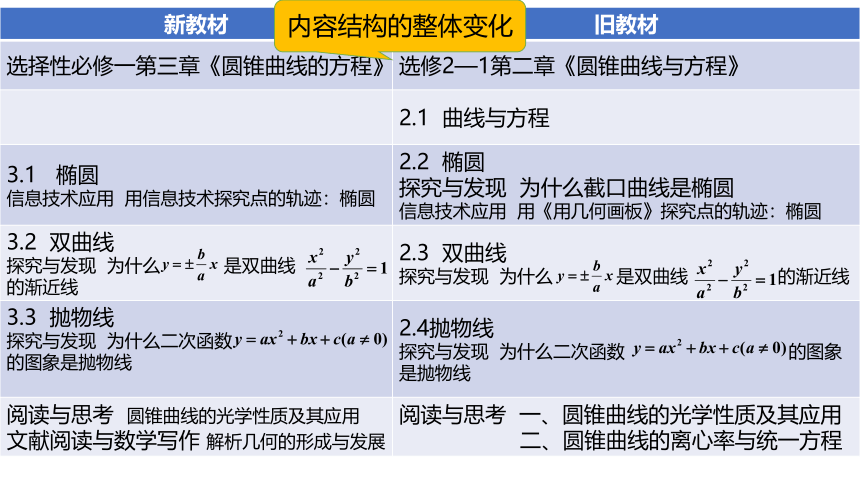
新教材 旧教材
选择性必修一第三章《圆锥曲线的方程》 选修2—1第二章《圆锥曲线与方程》
2.1 曲线与方程
3.1 椭圆 信息技术应用 用信息技术探究点的轨迹:椭圆 2.2 椭圆
探究与发现 为什么截口曲线是椭圆
信息技术应用 用《用几何画板》探究点的轨迹:椭圆
3.2 双曲线 探究与发现 为什么 是双曲线 的渐近线 2.3 双曲线
探究与发现 为什么 是双曲线 的渐近线
3.3 抛物线 探究与发现 为什么二次函数 的图象是抛物线 2.4抛物线
探究与发现 为什么二次函数 的图象是抛物线
阅读与思考 圆锥曲线的光学性质及其应用 文献阅读与数学写作 解析几何的形成与发展 阅读与思考 一、圆锥曲线的光学性质及其应用
二、圆锥曲线的离心率与统一方程
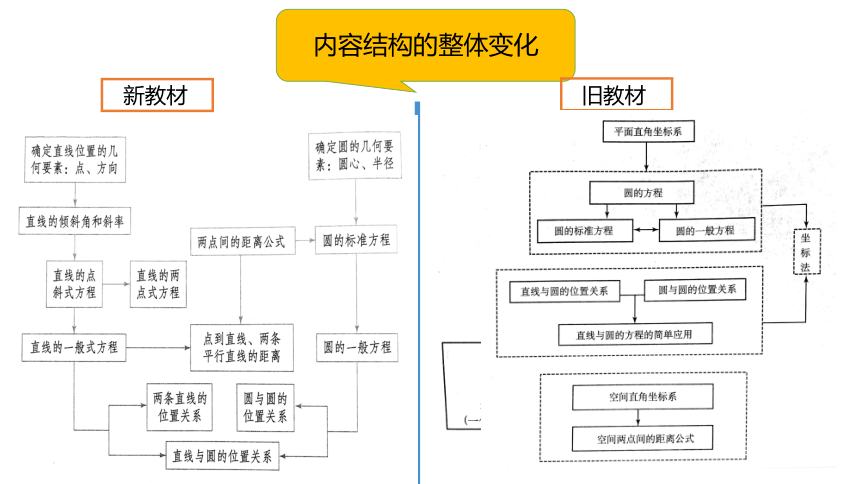
内容结构的整体变化
内容结构的整体变化
新教材
旧教材
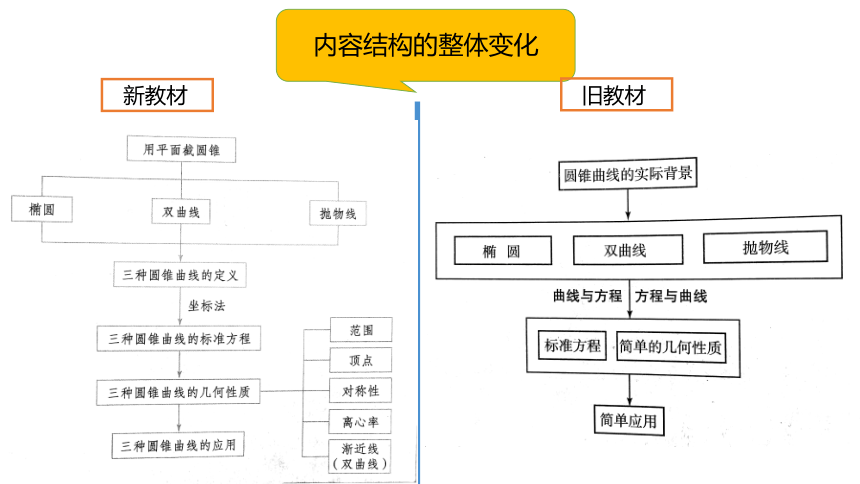
内容结构的整体变化
新教材
旧教材
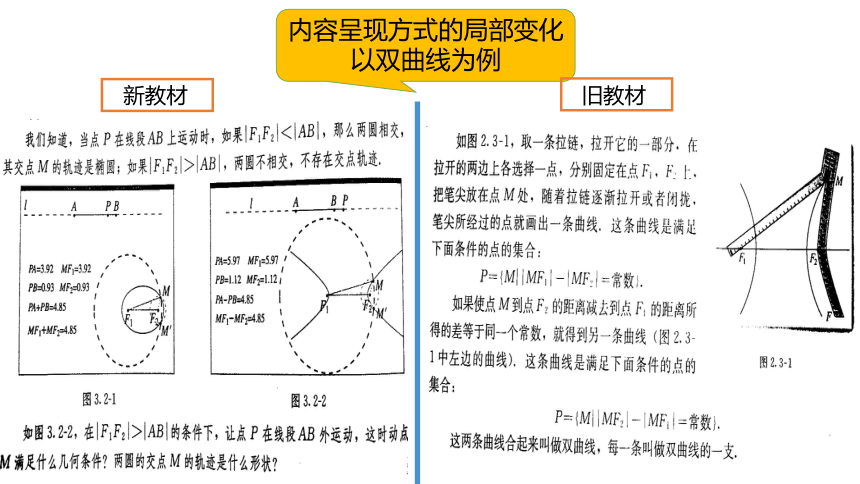
内容呈现方式的局部变化
以双曲线为例
新教材
旧教材
解析几何在高考中的地位
03
解析几何在高中数学中占有重要地位,是高考考查的重点内容之一,有一定的综合性。本模块内容在高考中将近占有百分之二十左右的分值,对学生的高考成绩有着直接的影响。
解析几何在高考中的地位
多选第一题
填空第一题
2020全国新高考I卷
2020全国新高考I卷
定点定值问题
2021全国新高考I卷
填空第二题
2021全国新高考I卷
定值问题
2022全国新高考I卷
多选第三题
填空第四题
2022全国新高考I卷
定值问题
已知PA和QA斜率和为0,
求(1)求直线l的斜率;
法一:线参法一:设直线PQ方程(求什么设什么)
已知PA和QA斜率和为0,
求(1)求直线l的斜率;
法二:线参法二:设直线AP、AQ方程(设而求)
已知PA和QA斜率和为0,
求(1)求直线l的斜率;
法三:点参法:设P、Q两点坐标(点差法)
已知PA和QA斜率和为0,
求(1)求直线l的斜率;
法四:直线参数法:
已知PA和QA斜率和为0,
求(1)求直线l的斜率;
法五:坐标平移法:
已知PA和QA斜率和为0,
求(1)求直线l的斜率;
法六:齐次化简法:
已知PA和QA斜率和为0,
求(1)求直线l的斜率;
法七:极限思想法:(无限逼近)
试题背景
倾角互补,连线定角
试题背景
倾角互补,面积最大
试题背景
斜率积定,连线过定点
2009江苏高中数学联赛解答题3:
联系1
2011全国高中数学联赛11:
联系2
2017全国卷理数20:
联系3
2018江苏高中数学联赛解答题3:
联系4
2021年新高考1卷21:
联系5
教学建议
04
教学启示
01
02
05
03
04
把握命题特点
夯实必备知识
优化学科素养
提高备考效能
提升关键能力
教学启示
明方向:椭圆、双曲线、抛物线
获能力:分析、画图、计算
重思想:数形结合、转化与化归
讲深度:数学背景、结论性质
提素养:落实核心素养,渗透立德树人
感谢各位老师观看!
不妥之处请批评指正!
抓基础、重计算、提素养
选择性必修第一册第二章第三章解析几何
3.解析几何在高考中的地位
4.教学建议
试题分析,说解题思路
1.备课组计划和有特色教学措施
2.新旧教材解析几何内容解读
备课组计划和有特色措施
01
备课组计划
依据统一安排,本学期主要完成解析几何、数列、统计的相关内容教学,目前没有增加其他内容的打算,因为本学期的内容相对难度较大,因而需要更多的课时来加强学生的学习与理解。
备课组措施
依照学生学习的实际,结合课标的基本理念,每个内容的教学,也要遵循着螺旋上升的意识,重视复习总结与提升的安排。
在具体的教学中,采用集体备课形式,以组内专家型教师为引领,发挥各位教师的主观能动性,备好每一堂课。备课组针对本年级学生的实际情况,充分利用并完善上届备课组自编的一课一练习题,习题配置难度、题量适中,重点关注数学本质的深度挖掘。
新旧教材解析几何内容解读
02
新教材 旧教材
选择性必修一第二章《直线和圆的方程》 必修二第三章《直线与方程》
2.1 直线的倾斜角与斜率 3.1 直线的倾斜角与斜率
探究与发现 魔术师的地毯
2.2 直线的方程 探究与发现 方向向量与直线的参数方程 3.2 直线的方程
2.3 直线的交点坐标与距离公式 阅读与思考 笛卡尔与解析几何 3.3 直线的交点坐标与距离公式
阅读与思考 笛卡尔与解析几何
必修二第四章《圆与方程》
2.4 圆的方程 阅读与思考 坐标法与数学机械化 4.1 圆的方程
阅读与思考 坐标法与机器证明
2.5 直线与圆、圆与圆的位置关系 4.2 直线、圆的位置关系
4.3 空间直角坐标系
信息技术应用《用几何画板》探究点的轨迹:圆
放入选择性必修一第一章
内容结构的整体变化
新教材 旧教材
选择性必修一第三章《圆锥曲线的方程》 选修2—1第二章《圆锥曲线与方程》
2.1 曲线与方程
3.1 椭圆 信息技术应用 用信息技术探究点的轨迹:椭圆 2.2 椭圆
探究与发现 为什么截口曲线是椭圆
信息技术应用 用《用几何画板》探究点的轨迹:椭圆
3.2 双曲线 探究与发现 为什么 是双曲线 的渐近线 2.3 双曲线
探究与发现 为什么 是双曲线 的渐近线
3.3 抛物线 探究与发现 为什么二次函数 的图象是抛物线 2.4抛物线
探究与发现 为什么二次函数 的图象是抛物线
阅读与思考 圆锥曲线的光学性质及其应用 文献阅读与数学写作 解析几何的形成与发展 阅读与思考 一、圆锥曲线的光学性质及其应用
二、圆锥曲线的离心率与统一方程
内容结构的整体变化
内容结构的整体变化
新教材
旧教材
内容结构的整体变化
新教材
旧教材
内容呈现方式的局部变化
以双曲线为例
新教材
旧教材
解析几何在高考中的地位
03
解析几何在高中数学中占有重要地位,是高考考查的重点内容之一,有一定的综合性。本模块内容在高考中将近占有百分之二十左右的分值,对学生的高考成绩有着直接的影响。
解析几何在高考中的地位
多选第一题
填空第一题
2020全国新高考I卷
2020全国新高考I卷
定点定值问题
2021全国新高考I卷
填空第二题
2021全国新高考I卷
定值问题
2022全国新高考I卷
多选第三题
填空第四题
2022全国新高考I卷
定值问题
已知PA和QA斜率和为0,
求(1)求直线l的斜率;
法一:线参法一:设直线PQ方程(求什么设什么)
已知PA和QA斜率和为0,
求(1)求直线l的斜率;
法二:线参法二:设直线AP、AQ方程(设而求)
已知PA和QA斜率和为0,
求(1)求直线l的斜率;
法三:点参法:设P、Q两点坐标(点差法)
已知PA和QA斜率和为0,
求(1)求直线l的斜率;
法四:直线参数法:
已知PA和QA斜率和为0,
求(1)求直线l的斜率;
法五:坐标平移法:
已知PA和QA斜率和为0,
求(1)求直线l的斜率;
法六:齐次化简法:
已知PA和QA斜率和为0,
求(1)求直线l的斜率;
法七:极限思想法:(无限逼近)
试题背景
倾角互补,连线定角
试题背景
倾角互补,面积最大
试题背景
斜率积定,连线过定点
2009江苏高中数学联赛解答题3:
联系1
2011全国高中数学联赛11:
联系2
2017全国卷理数20:
联系3
2018江苏高中数学联赛解答题3:
联系4
2021年新高考1卷21:
联系5
教学建议
04
教学启示
01
02
05
03
04
把握命题特点
夯实必备知识
优化学科素养
提高备考效能
提升关键能力
教学启示
明方向:椭圆、双曲线、抛物线
获能力:分析、画图、计算
重思想:数形结合、转化与化归
讲深度:数学背景、结论性质
提素养:落实核心素养,渗透立德树人
感谢各位老师观看!
不妥之处请批评指正!
同课章节目录
