核心素养视域下高中立体几何教学策略分析 课件(28张PPT)
文档属性
| 名称 | 核心素养视域下高中立体几何教学策略分析 课件(28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 60.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 15:24:21 | ||
图片预览








文档简介
(共28张PPT)
核心素养视域下高中立体几何教学策略分析
——以“与球有关的切与接问题”为例
目 录
01
真题分析
02
考情学情
03
教学策略
延迟符
延迟符
真题分析
数学课程标准(2017年版2020年修订)
①认识柱、锥、台、球及简单组合体的结构特征,能用这些特征描述现实生活中简单物体的结构。
②知道球、棱柱、棱锥、棱台的表面积和体积的计算公式,能用公式解决简单的实际问题。
浙江省普通高中学科教学指导意见(2021年8月)
认识柱、锥、台、球的结构特征,了解与正方体、球有关的简单组合体及其结构特征。能根据条件判断几何体的类型。
2019-2022年全国卷数学高考有关球的试题
年份 卷型题型·题号 分值 题涉考点 难度
2022 新高考1卷单选题·8 5分 锥体体积、球体体积、多面体与球内切外接、函数导数(基本不等式)求最值 难
新高考2卷单选题·7 5分 球的表面积、多面体与球内切外接 中
乙卷理科(文科)单选题·9(12) 4分 多面体与球内切外接、锥体体积、基本不等式(也可用函数导数)求最值 中
2021 甲卷理科选择题·11 4分 球内几何体、几何体的体积 中
新高考2卷单选题·4 5分 球的表面积和体积公式、数学文化与应用 易
2020 新高考1卷2卷单选题·4 5分 平面平行、线面垂直、古代数学文化、线面角 中
1卷理科(文科)选择题·10(12) 4分 球的表面积、球的截面性质 中
2卷文科单选题·11 4分 球的表面积、球的截面性质 中
3卷理科填空題·15 4分 圆锥内切球、球体体积、截面性质 中
2019 1卷理科选择题·12 4分 正方体外接球、线面垂直、球的体积 中
球体体积、表面积、多面体与球内切外接、
线面位置关系、与不等式、函数相结合等问题。
考查内容
考查难度
考查题型
考查能力
简单、中档、难题均有,近四年以中档题为主。
选择题或者填空题,一题。
数学运算、空间想象能力、逻辑推理能力。难题考察知识的综合应用能力。
01
高考中的球
重 基 础
会 画 图
能 计 算
1
2
3
4
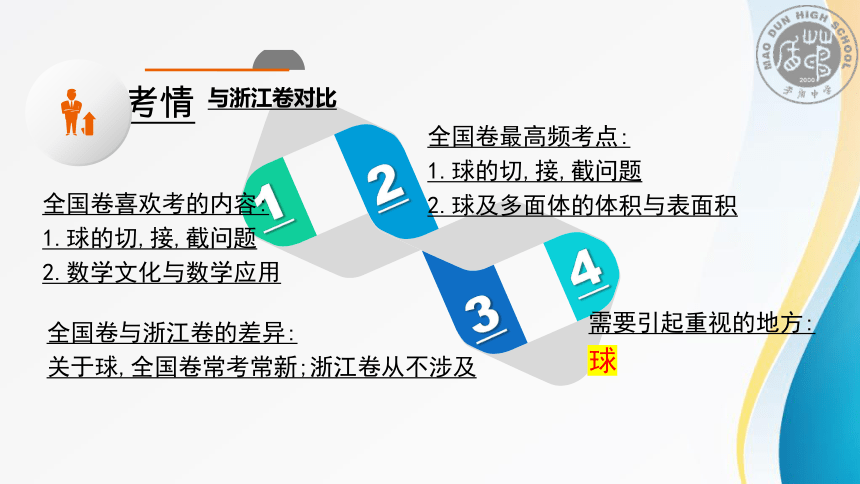
全国卷喜欢考的内容:
1.球的切,接,截问题
2.数学文化与数学应用
需要引起重视的地方:
球
全国卷最高频考点:
1.球的切,接,截问题
2.球及多面体的体积与表面积
全国卷与浙江卷的差异:
关于球,全国卷常考常新;浙江卷从不涉及
考情
与浙江卷对比
02
学情分析
1.学生基础知识薄弱,立体几何模块整体知识的灵活应用能力不足
2.数形结合和空间想象能力不够
3.转化与化归能力的缺乏(缺少建构基本模型如:正方体、长方体、正四面体外接球内切球等)
4.数学运算能力差,缺乏必要的运算技巧(含参运算、解方程组、整体代换)
5.立体几何学习上具有畏惧心理,缺乏自信心
延迟符
延迟符
教学策略
一、注重直观感知和作图能力,培养直观想象
例1已知∠ABC=90°,PA⊥平面ABC,若PA=AB=BC=1,则四面体PABC的外接球(顶点都在球面上)的体积为
√
一、注重直观感知和作图能力,培养直观想象
例1(变式)已知∠ABC=60°,PA⊥平面ABC,若PA=AB=BC=1,则四面体PABC的外接球(顶点都在球面上)的体积为
二、通过问题变式,深化逻辑推理的能力
二、通过问题变式,深化逻辑推理的能力
变式1 条件不变,求此时三棱锥内切球的表面积。
变式2 条件不变,求点O到平面ABC的距离。
这个变式也是2020年全国Ⅱ卷理科第10题的题源 。
二、通过问题变式,深化逻辑推理的能力
也是2021年全国甲卷理科第11题的题源 。
三、注重模型化与平面化的培养
补形为长方体
思考:例1还有别的方法解决吗?
例1已知∠ABC=90°,PA⊥平面ABC,若PA=AB=BC=1,则四面体PABC的外接球(顶点都在球面上)的体积为
②若球为正方体的内切球,则2R=a;
√
例3. 已知三棱锥P-ABC中,PA,PB,PC两两垂直,且PA=1,PB=2,PC=3,则三棱锥P-ABC的外接球的表面积为
三、注重模型化与平面化的培养
一
柱体背景的模型--模型1.墙角模型
补形为长方体
三、注重模型化与平面化的培养
一
柱体背景的模型--模型1.墙角模型
补形为正方体
(湖丽衢2022.11月联考单选题5)
三、注重模型化与平面化的培养
柱体背景的模型--模型1.墙角模型
关键点找到三条两两垂直的线段,直接用公式(2R)2=a2+b2+c2
A.2π B.4π C.6π D.8π
√
三、注重模型化与平面化的培养
模型2.对棱相等模型
补形为长方体
三、注重模型化与平面化的培养
模型3.汉堡模型
(直棱柱的外接球,圆柱的外接球,有一侧棱垂直于底面的多面体)
关键点确定球心O的位置,底面小圆圆心O1,OO1⊥底面,利用勾股定理(R)2=OO12+AO12
三、注重模型化与平面化的培养
锥体背景的模型--模型4.切瓜模型
截面法
关键点是抓住球的截面性质:
(1)球心与截面小圆圆心的连线垂直于截面;
(2)球的半径R,截面圆的半径r及球心到截面的距离d满足R2=r2+d2
√
例5(2022·新高考全国I卷·第8题) 已知正四棱锥的侧棱长为l,其各顶点都在同一球面上。若该球的体积为 ,且 ,则该正四棱锥体积的取值范围是( )
(两个大小圆面互相垂直且交于小圆直径)
三、注重模型化与平面化的培养
锥体背景的模型--模型5.锥体内切球模型
与球截面有关的解题策略
①定球心:如果是内切球,球心到切点的距离相等且为半径;如果是外接球,球心到接点的距离相等且为半径;
②作截面:选准最佳角度作出截面,达到空间问题平面化的目的.
三、注重模型化与平面化的培养
二面角背景的模型--模型6.折叠模型
(两个全等三角形或等腰三角形拼在一起,或菱形折叠)
解决问题的基本方法是找到合适的模型,然后将三维空间图形转化为二维平面中图形的位置关系,球的截面的性质。解题关键是找到模型,会画三图和补形。
三、注重模型化与平面化的培养
四、注重转化与化归思想的培养
通过变式问题链设计,以及将题型模型化处理后,学生由浅入深地展开思考,并在不断推理中深化外接球、内切球问题的解决方法与技巧,训练学生化归与转化思想,降维思考。选准最佳角度作图,达到空间问题平面化的目的.
空间问题
平面问题
一般模型
特殊模型
五、结语
在“与球有关的切与接问题”教学中,学生核心素养与解题能力的培育应注重:①坚持回归基础,从球心的定义找球心,掌握球与多面体的内切、外接性质;②深化通解通法,从高考真题出发,结合变式训练,建立多元化的解题应变策略;③掌握综合知识,从加强学生识图、作图、想图的训练,培养学生空间想象能力和逻辑推理能力。还要结合方程思想、不等式的应用、函数思想等知识应用,全面提升学生转化与化归思想、数形结合思想、运算能力等综合素养。
六、疑问
课标对球的要求不高,和其他几何体的要求一致,没有对球特别提出更高要求,在平时教学中对于球内容和难度上应该教到什么样的程度?
高考近几年的考题是为了考察球特意而为之吗?亦或是偶然,未来几年可能会变其他几何体的组合体考察吗?
感 谢 聆 听!
核心素养视域下高中立体几何教学策略分析
——以“与球有关的切与接问题”为例
目 录
01
真题分析
02
考情学情
03
教学策略
延迟符
延迟符
真题分析
数学课程标准(2017年版2020年修订)
①认识柱、锥、台、球及简单组合体的结构特征,能用这些特征描述现实生活中简单物体的结构。
②知道球、棱柱、棱锥、棱台的表面积和体积的计算公式,能用公式解决简单的实际问题。
浙江省普通高中学科教学指导意见(2021年8月)
认识柱、锥、台、球的结构特征,了解与正方体、球有关的简单组合体及其结构特征。能根据条件判断几何体的类型。
2019-2022年全国卷数学高考有关球的试题
年份 卷型题型·题号 分值 题涉考点 难度
2022 新高考1卷单选题·8 5分 锥体体积、球体体积、多面体与球内切外接、函数导数(基本不等式)求最值 难
新高考2卷单选题·7 5分 球的表面积、多面体与球内切外接 中
乙卷理科(文科)单选题·9(12) 4分 多面体与球内切外接、锥体体积、基本不等式(也可用函数导数)求最值 中
2021 甲卷理科选择题·11 4分 球内几何体、几何体的体积 中
新高考2卷单选题·4 5分 球的表面积和体积公式、数学文化与应用 易
2020 新高考1卷2卷单选题·4 5分 平面平行、线面垂直、古代数学文化、线面角 中
1卷理科(文科)选择题·10(12) 4分 球的表面积、球的截面性质 中
2卷文科单选题·11 4分 球的表面积、球的截面性质 中
3卷理科填空題·15 4分 圆锥内切球、球体体积、截面性质 中
2019 1卷理科选择题·12 4分 正方体外接球、线面垂直、球的体积 中
球体体积、表面积、多面体与球内切外接、
线面位置关系、与不等式、函数相结合等问题。
考查内容
考查难度
考查题型
考查能力
简单、中档、难题均有,近四年以中档题为主。
选择题或者填空题,一题。
数学运算、空间想象能力、逻辑推理能力。难题考察知识的综合应用能力。
01
高考中的球
重 基 础
会 画 图
能 计 算
1
2
3
4
全国卷喜欢考的内容:
1.球的切,接,截问题
2.数学文化与数学应用
需要引起重视的地方:
球
全国卷最高频考点:
1.球的切,接,截问题
2.球及多面体的体积与表面积
全国卷与浙江卷的差异:
关于球,全国卷常考常新;浙江卷从不涉及
考情
与浙江卷对比
02
学情分析
1.学生基础知识薄弱,立体几何模块整体知识的灵活应用能力不足
2.数形结合和空间想象能力不够
3.转化与化归能力的缺乏(缺少建构基本模型如:正方体、长方体、正四面体外接球内切球等)
4.数学运算能力差,缺乏必要的运算技巧(含参运算、解方程组、整体代换)
5.立体几何学习上具有畏惧心理,缺乏自信心
延迟符
延迟符
教学策略
一、注重直观感知和作图能力,培养直观想象
例1已知∠ABC=90°,PA⊥平面ABC,若PA=AB=BC=1,则四面体PABC的外接球(顶点都在球面上)的体积为
√
一、注重直观感知和作图能力,培养直观想象
例1(变式)已知∠ABC=60°,PA⊥平面ABC,若PA=AB=BC=1,则四面体PABC的外接球(顶点都在球面上)的体积为
二、通过问题变式,深化逻辑推理的能力
二、通过问题变式,深化逻辑推理的能力
变式1 条件不变,求此时三棱锥内切球的表面积。
变式2 条件不变,求点O到平面ABC的距离。
这个变式也是2020年全国Ⅱ卷理科第10题的题源 。
二、通过问题变式,深化逻辑推理的能力
也是2021年全国甲卷理科第11题的题源 。
三、注重模型化与平面化的培养
补形为长方体
思考:例1还有别的方法解决吗?
例1已知∠ABC=90°,PA⊥平面ABC,若PA=AB=BC=1,则四面体PABC的外接球(顶点都在球面上)的体积为
②若球为正方体的内切球,则2R=a;
√
例3. 已知三棱锥P-ABC中,PA,PB,PC两两垂直,且PA=1,PB=2,PC=3,则三棱锥P-ABC的外接球的表面积为
三、注重模型化与平面化的培养
一
柱体背景的模型--模型1.墙角模型
补形为长方体
三、注重模型化与平面化的培养
一
柱体背景的模型--模型1.墙角模型
补形为正方体
(湖丽衢2022.11月联考单选题5)
三、注重模型化与平面化的培养
柱体背景的模型--模型1.墙角模型
关键点找到三条两两垂直的线段,直接用公式(2R)2=a2+b2+c2
A.2π B.4π C.6π D.8π
√
三、注重模型化与平面化的培养
模型2.对棱相等模型
补形为长方体
三、注重模型化与平面化的培养
模型3.汉堡模型
(直棱柱的外接球,圆柱的外接球,有一侧棱垂直于底面的多面体)
关键点确定球心O的位置,底面小圆圆心O1,OO1⊥底面,利用勾股定理(R)2=OO12+AO12
三、注重模型化与平面化的培养
锥体背景的模型--模型4.切瓜模型
截面法
关键点是抓住球的截面性质:
(1)球心与截面小圆圆心的连线垂直于截面;
(2)球的半径R,截面圆的半径r及球心到截面的距离d满足R2=r2+d2
√
例5(2022·新高考全国I卷·第8题) 已知正四棱锥的侧棱长为l,其各顶点都在同一球面上。若该球的体积为 ,且 ,则该正四棱锥体积的取值范围是( )
(两个大小圆面互相垂直且交于小圆直径)
三、注重模型化与平面化的培养
锥体背景的模型--模型5.锥体内切球模型
与球截面有关的解题策略
①定球心:如果是内切球,球心到切点的距离相等且为半径;如果是外接球,球心到接点的距离相等且为半径;
②作截面:选准最佳角度作出截面,达到空间问题平面化的目的.
三、注重模型化与平面化的培养
二面角背景的模型--模型6.折叠模型
(两个全等三角形或等腰三角形拼在一起,或菱形折叠)
解决问题的基本方法是找到合适的模型,然后将三维空间图形转化为二维平面中图形的位置关系,球的截面的性质。解题关键是找到模型,会画三图和补形。
三、注重模型化与平面化的培养
四、注重转化与化归思想的培养
通过变式问题链设计,以及将题型模型化处理后,学生由浅入深地展开思考,并在不断推理中深化外接球、内切球问题的解决方法与技巧,训练学生化归与转化思想,降维思考。选准最佳角度作图,达到空间问题平面化的目的.
空间问题
平面问题
一般模型
特殊模型
五、结语
在“与球有关的切与接问题”教学中,学生核心素养与解题能力的培育应注重:①坚持回归基础,从球心的定义找球心,掌握球与多面体的内切、外接性质;②深化通解通法,从高考真题出发,结合变式训练,建立多元化的解题应变策略;③掌握综合知识,从加强学生识图、作图、想图的训练,培养学生空间想象能力和逻辑推理能力。还要结合方程思想、不等式的应用、函数思想等知识应用,全面提升学生转化与化归思想、数形结合思想、运算能力等综合素养。
六、疑问
课标对球的要求不高,和其他几何体的要求一致,没有对球特别提出更高要求,在平时教学中对于球内容和难度上应该教到什么样的程度?
高考近几年的考题是为了考察球特意而为之吗?亦或是偶然,未来几年可能会变其他几何体的组合体考察吗?
感 谢 聆 听!
同课章节目录
