2023届高中数学二轮复习专题三立体几何 课件(170张)
文档属性
| 名称 | 2023届高中数学二轮复习专题三立体几何 课件(170张) |  | |
| 格式 | zip | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 14:27:48 | ||
图片预览











文档简介
(共170张PPT)
专题三 立体几何
上篇
2023
内容索引
01
02
03
高考小题突破4 空间几何体的结构、表面积与体积
◎高考保分大题三 立体几何中的证明与计算
培优拓展 立体几何中的动态、最值问题
04
培优拓展 立体几何中的截面、交线问题
考情分析 1.从题型和题量上看,高考对本专题考查基本稳定在“两小一大”的方式,总分约22分.
2.从考查内容上看,小题主要考查空间几何体的结构特征、体积与表面积、球与几何体的“切”“接”、空间位置关系的判断等,难度中等或中低等.解答题多以几何体为载体,考查空间位置关系的证明、空间角的求解等,难度中等.
3.核心素养:直观想象、逻辑推理、数学运算等.
备考策略 1.掌握特殊几何体的结构特征,熟记体积与表面积公式,理解并会应用空间平行与垂直的相关定理与结论,这是解决立体几何问题的基础.
2.注意对空间想象核心素养的训练,通过动手画图,观察分析图形,对空间几何体中位置关系的证明与应用等,都可以有效提升空间想象能力.
3.重视图形的作用,解立体几何问题,可将题目已知或隐含的条件标注在图形上,达到只通过图形就能表述出题目的已知与所求的效果.
4.归纳几何体中常见的建系方法与技巧,并能合理运用.
5.通过题目的训练,提升运算正确率,尤其是利用空间向量求解空间角的问题.
真题感悟
A.100π B.128π
C.144π D.192π
答案 A
解析 设外接球的半径为R,由题意得,上底面所在平面截球所得圆的半径是3,下底面所在平面截球所得圆的半径是4,在轴截面中,设球心到上下底面
2.(2021·全国乙·理5)在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为( )
答案 D
解析 如图,连接BC1,PC1.
3.(2020·全国Ⅰ·理10)已知A,B,C为球O的球面上的三个点,☉O1为△ABC的外接圆.若☉O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为( )
A.64π B.48π
C.36π D.32π
答案 A
4.(2021·全国甲·文14)已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为 .
答案 39π
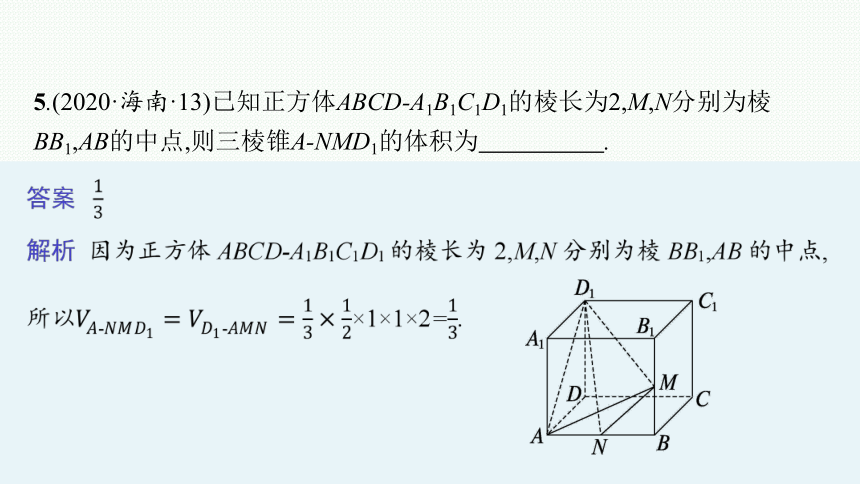
5.(2020·海南·13)已知正方体ABCD-A1B1C1D1的棱长为2,M,N分别为棱BB1,AB的中点,则三棱锥A-NMD1的体积为 .
6. (2022·全国甲·理18)在四棱锥P-ABCD中,PD⊥底面ABCD,
CD∥AB,AD=DC=CB=1,AB=2,DP= .
(1)证明:BD⊥PA;
(2)求PD与平面PAB所成的角的正弦值.
(1)证明 ∵PD⊥平面ABCD,BD 平面ABCD,∴PD⊥BD.取AB的中点E,连接DE.
∵CD=1,BE= AB=1,CD∥BE,
∴四边形CDEB是平行四边形,∴DE=CB=1.
∵DE= AB,∴△ABD为直角三角形,AB为斜边,
∴BD⊥AD.
∵PD 平面PAD,AD 平面PAD,且PD∩AD=D,
∴BD⊥平面PAD.又PA 平面PAD,∴BD⊥PA.
(2)解 由(1)知,PD,AD,BD两两垂直,以点D为坐标原点,DA,DB,DP所在直线分别为x轴、y轴、z轴建立如图所示空间直角坐标系,其中
7. (2022·新高考Ⅰ·19)如图,直三棱柱ABC-A1B1C1的体积为4,△A1BC的面
(1)求A到平面A1BC的距离;
(2)设D为A1C的中点,AA1=AB,平面A1BC⊥平面ABB1A1,求二面角A-BD-C的正弦值.
∵AA1=AB,∴AB1⊥A1B.又平面A1BC⊥平面ABB1A1,平面A1BC∩平面ABB1A1=A1B,∴AB1⊥平面A1BC.
又BC 平面A1BC,∴BC⊥AB1,又BC⊥BB1,AB1,BB1 平面ABB1A1,且AB1∩BB1=B1,
∴BC⊥平面ABB1A1,∴BC⊥AB,BC⊥A1B.
h=BC=2.
∴点A(0,2,0),B(0,0,0),D(1,1,1),E(0,1,1).
设n1=(x1,y1,z1)为平面ABD的一个法向量.
知识精要
1.空间几何体的表面积与体积公式
球的表面积的大小恰好是球的大圆面积大小的4倍
名师点析
1.圆柱、圆锥、圆台的体积公式之间的关系
2.柱体、锥体、台体的体积公式之间的关系
2.线面、面面平行的判定及性质定理
①线面平行的判定定理:a α,b α,a∥b a∥α;
②线面平行的性质定理:a∥α,a β,α∩β=b a∥b;
③面面平行的判定定理:a α,b α,a∥β,b∥β,a∩b=P α∥β;
④面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b a∥b.
3.线面、面面垂直的判定及性质定理
①线面垂直的判定定理:m α,n α,m∩n=P,l⊥m,l⊥n l⊥α;
②线面垂直的性质定理:a⊥α,b⊥α a∥b;
③面面垂直的判定定理:a β,a⊥α β⊥α;
④面面垂直的性质定理:α⊥β,α∩β=l,a α,a⊥l a⊥β.
4.利用空间向量求空间角
(1)两条异面直线所成的角:设异面直线l,m的方向向量分别为a,b,且它们所
公式两边都有绝对值,所以两角相等或互补
名师点析
利用空间向量求空间角时,一定要注意角的取值范围.对于二面角,要注意题目条件是
否明确是锐角还是钝角,如果没有说明,则结合图形特点判断.若求两个不平行平面的夹角,则取直角或锐角.
5.利用空间向量求点到平面的距离
如图所示,已知AB为平面α的一条斜线段,n为平面α的法向量,则点B到平面
常用结论
2.空间几何体中的常用结论
(1)若长方体从一个顶点出发的三条棱长分别为a,b,c,则其外接球的直径为
(2)正四面体(棱长都为a)的几个结论:
正四面体是特殊的正三棱锥,正三棱锥不一定是正四面体
(3)正方体与球的几个结论:
高考小题突破4
考点一
空间几何体的结构特征
(2)(2020·全国Ⅰ·理3)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
答案 (1)B (2)C
解析 (1)设圆锥底面半径为r1,圆锥侧面展开图半圆所在圆的半径为r2.
图①
图②
增分技巧
几何体的表面展开及其应用
(1)圆锥、圆柱的侧面展开图分别为扇形
和矩形,圆锥、圆柱的底面周长分别为扇形的弧长、矩形的一边长,据此建立圆锥、圆柱基本量的联系解决问题.
(2)解决多面体或旋转体的表面上与长度有关的最值问题时,一般采用转化法,即将表面展开化为平面图形,通过“化折为直”或“化曲为直”来解决,注意展开前后哪些几何量发生变化,哪些不变.
(2)(2022·河北秦皇岛二模)在长方体ABCD-A1B1C1D1中,AB=2,AD=3,
A1A=1,P为线段C1D1的中点,一质点从A点出发,沿长方体表面运动到达P点处,则质点从A到P的最短距离为 ;若沿质点A的最短运动路线截长方体,则所得截面的面积为 .
图1
图2
图3
此时质点从A点出发,经过A1D1的中点E,再到达P点,则平面AEP截长方体所得的截面为梯形ACPE,如图5所示,
图4
图5
考点二
空间几何体的表面积与体积
考向1空间几何体的表面积
典例突破2(1)(多选)(2022·湖北武汉模拟)一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R相等,下列结论正确的是( )
A.圆柱的侧面积为4πR2
B.圆锥的侧面积为2πR2
C.圆柱的侧面积与球的表面积相等
D.球的体积是圆锥体积的两倍
(2)(2022·辽宁锦州一模)“水立方”的设计灵感来自威尔·弗兰泡沫,威尔·弗兰泡沫是对开尔文胞体的改进,开尔文胞体是一种多面体,它由正六边形和正方形围成(其中每一个顶点处有一个正方形和两个正六边形),已知该多面体共有24个顶点,且棱长为2,则该多面体的表面积是( )
答案 (1)ACD (2)C
解析 (1)对于A,∵圆柱的底面直径和高都等于2R,∴圆柱的侧面积S1=2πR·2R=4πR2.故A正确;对于B,∵圆锥的底面直径和高等于2R,
(2)由题得,棱长为2的正方形的面积为2×2=4,正六边形的面积为
24个顶点,所以最多有6个正方形,最少有4个正六边形,1个正六边形与3个正方形相连,所以该多面体有6个正方形,则正六边形有6×4÷3=8(个).
增分技巧
空间几何体表面积的求法
(1)求表面积问题的思路是将立体几何问题转化为平面几何问题,即空间图形平面化,这是解决立体几何问题的主要出发点.
(2)求不规则几何体的表面积时,通常将所给几何体分割成柱体、锥体、台体,先求出这些柱体、锥体、台体的表面积,再通过求和或作差求得所给几何体的表面积.
对点练2
(1)(2022·福建福州模拟)如图,一个正六棱柱的茶叶盒,底面边长为10 cm,高为20 cm,则这个茶叶盒的表面积约为 cm2.(精确到0.1, ≈1.732)
(2)(2022·广东惠州一模)若一个圆台的侧面展开图是半圆面所在的扇环,且扇环的面积为4π,圆台上、下底面圆的半径分别为r1,r2(r1答案 (1)1 719.6 (2)2
200+300×1.732=1 719.6(cm2).
(2)因为圆台的侧面展开图是半圆面所在的扇环,所以圆台的母线长为
考向2空间几何体的体积
典例突破3(1)(2022·新高考Ⅰ·4)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5 m时,相应水面的面积为140.0 km2;水位为海拔157.5 m时,相应水面的面积为180.0 km2.将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5 m上升到157.5 m时,增加的水量约为( ≈2.65)( )
A.1.0×109 m3 B.1.2×109 m3
C.1.4×109 m3 D.1.6×109 m3
(2)(2021·北京·8)某一时间段内,从天空降落到地面上的雨水,未经蒸发、渗漏、流失而在水平面上积聚的深度,称为这个时段的降雨量(单位:mm).24 h降雨量的等级划分如下:
等级 24 h降雨量(精确到0.1)
…… ……
小雨 0.1~9.9
中雨 10.0~24.9
大雨 25.0~49.9
暴雨 50.0~99.9
…… ……
在综合实践活动中,某小组自制了一个底面直径为200 mm,高为300 mm的圆锥形雨量器.若一次降雨过程中,该雨量器收集的24 h的雨水高度是150 mm(如图所示),则这24 h降雨量的等级是( )
A.小雨 B.中雨
C.大雨 D.暴雨
答案 (1)C (2)B
解析 (1)由题意可得,此棱台的高h=157.5-148.5=9(m).
设水库水位为海拔148.5 m时,相应水面的面积为S1,水库水位为海拔157.5 m时,相应水面的面积为S2,则S1=140.0 km2=1.4×108 m2,S2=180.0 km2
即增加的水量约为1.4×109 m3.故选C.
增分技巧
求几何体体积的基本方法
(1)直接法:对于规则的几何体,可利用相关公式直接计算求解.
(2)割补法:对于不规则的几何体,可将其分割成规则的几何体,进行体积计算;也可把不规则的几何体补成规则的几何体,进行体积计算.
(3)转换法:主要用于求三棱锥(四面体)的体积,将三棱锥的顶点和底面进行转换,使其底面的面积可求(或容易求),高可求(或容易求),从而代入公式求得体积.
对点练3(1)某品牌暖水瓶的内胆规格如图所示,分为①②③④四个部分(水瓶内胆壁厚不计),它们分别为一个半球、一个大圆柱、一个圆台和一个小圆柱.若其中圆台部分的体积为52π cm3,且水瓶灌满水后盖上瓶塞时水溢
(2)(2019·全国Ⅲ·16)学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm.3D打印所用原料密度为0.9 g/cm3.不考虑打印损耗,制作该模型所需原料的质量为 g.
答案 (1)A (2)118.8
ABCD-A1B1C1D1的体积为V2=4×6×6=144(cm3),
则该模型的体积为V=V2-V1=144-12=132(cm3).故其质量为0.9×132=118.8(g).
考点三
球的“切”“接”问题
考向1外接球问题
典例突破4(1)(2021·天津·6)两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为 ,两个圆锥的高之比为1∶3,则这两个圆锥的体积之和为( )
A.3π B.4π C.9π D.12π
(2)(2022·山东聊城一模)“阿基米德多面体”也称半正多面体,是由边数不全相同的正多边形围成的多面体.如图是以一正方体的各条棱的中点为顶点的多面体,这是一个有八个面为正三角形,六个面为正方形的“阿基米德多面体”,若该多面体的棱长为1,则经过该多面体的各个顶点的球的体积为( )
答案 (1)B (2)A
所以AB=AD+BD=4BD=4,
所以BD=1,AD=3.设两个圆锥的公共底面圆的半径为r,
增分技巧
解决几何体外接球问题的基本方法
(1)由球的定义确定球心.
①正方体或长方体的外接球的球心是其体对角线的中点.
②正棱柱的外接球的球心是上、下底面中心的连线的中点.
③直三棱柱的外接球的球心是上、下底面三角形外心的连线的中点.
④正棱锥的外接球的球心在其高上,具体位置可通过构造直角三角形,利用勾股定理求得.
(2)构造正方体或长方体确定球心.
①可构造正方体的情况:a.正四面体,其棱长对应正方体的面对角线长;b.三条侧棱两两垂直的正三棱锥,其底面边长对应正方体的面对角线长,侧棱长对应正方体的棱长.
②可构造长方体的情况:a.某一个顶点处的三条棱两两垂直的四面体;b.四个面都是直角三角形的三棱锥;c.相对的棱相等的三棱锥.
(3)利用性质确定球心.
对点练4
(1)(2022·广东佛山二模)如图,某几何体由共底面的圆锥和圆柱组合而成,且圆柱的两个底面和圆锥的顶点均在体积为36π的球面上,若圆柱的高为2,则圆锥的侧面积为( )
(2)(2022·湖南长沙高三调研)蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗产名录.已知某鞠的表面上有五个点P,A,B,C,D恰好构成一正四棱锥P-ABCD,若该棱锥的高为8,底面边长为4 ,则该鞠的表面积为( )
A.64π B.100π C.132π D.144π
答案 (1)B (2)B
解析 (1)依题意,作球的剖面图,其中O是球心,E是圆锥的顶点,EC是圆锥的母线.设球的半径为R,则 πR3=36π,解得R=3.
(2)依题意作图,∵P-ABCD是正四棱锥,
∴底面ABCD是正方形,且点P在底面的投影为正方形ABCD的中心O1,则PO1⊥平面ABCD.
∵外接球的球心在PO1上,设球心为O,连接BO,则BO为外接球的半径R.又PO1=8,PO=R,∴在Rt△BOO1中,BO2=(8-PO)2+B,即R2=(8-R)2+42,解得R=5,故外接球的表面积S=4πR2=100π.
考向2内切球问题
典例突破5(1)(2020·全国Ⅲ·文16)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为 .
(2)(2022·广东二模)如图,该十字贯穿体由两个全等的正四棱柱组合而成,且两个四棱柱的侧棱互相垂直,若底面正方形边长为2,则这两个正四棱柱公共部分所构成的几何体的内切球的体积为 .
解析 (1)(方法一)由题意可知该圆锥的轴截面为底边长为2,腰长为3的等腰三角形,其内切圆为该球的大圆.如图,SB=3,BC=1,
设该球内切于母线SB,切点为点O.
(方法二)由题意可知该圆锥的轴截面为底边长为2,腰长为3的等腰三角形,其内切圆为该球的大圆.
(2)如图所示,这两个正四棱柱公共部分所构成的几何体为两个全等的四棱锥S-ABCD和P-ABCD.
由题意,这两个直四棱柱的中心既是外接球的球心,也是
内切球的球心,设内切球的半径为R,线段AC的中点为H,
连接BH,SH,可知SH即为四棱锥S-ABCD的高.
增分技巧
求几何体内切球的半径的常用方法
(1)将空间问题转化为平面问题,通过构造直角三角形,利用平面知识求出内切球的半径.
(2)利用体积分割求出内切球的半径.
对点练5(1)(2022·湖南长郡中学模拟)如图,球与圆柱的侧面及上、下底面相切,设圆柱的体积与球的体积之比为m,圆柱的表面积与球的表面积之比
(2)(2022·山东烟台一模)如图,在三棱锥V-ABC中,VA⊥底面ABC,
∠BAC=90°,AB=AC=AV=2,则该三棱锥的内切球和外接球的半径之比为( )
答案 (1)B (2)C
解析 (1)设球的半径为R,则圆柱的底面圆的半径为R,高为2R,则圆柱的体积
(2)因为VA⊥底面ABC,AB,AC 底面ABC,所以VA⊥AB,VA⊥AC.因为∠BAC=90°,所以AB⊥AC,而AB=AC=AV=2,因为三条互相垂直且共顶点的棱,可以看成正方体中共顶点的三条棱,因此该三棱锥外接球的半径
高考保分大题三
保分1
空间中的平行与垂直
热点一 空间平行、垂直关系的证明与应用
典例突破1
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD= AD,E,F分别为线段PC,BD的中点.
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PDC.
证明 (1)连接AC,AC∩BD=F.因为四边形ABCD为正方形,F为线段AC中点,E为线段PC中点,所以在△CPA中,EF∥PA.
因为PA 平面PAD,EF 平面PAD,
所以EF∥平面PAD.
(2)在正方形ABCD中,CD⊥AD.
因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD 平面ABCD,所以CD⊥平面PAD,所以CD⊥PA.
又PA=PD= AD,所以△PAD是等腰直角三角形,且∠APD=90°,即PA⊥PD.因为CD∩PD=D,且CD,PD 平面PDC,所以PA⊥平面PDC.
又PA 平面PAB,所以平面PAB⊥平面PDC.
增分技巧
空间几何体中线面位置关系的判断方法
(1)明确空间几何体的结构特征,明确其中已有的平行、垂直关系.
(2)熟练掌握线面平行、面面平行、线面垂直、面面垂直的判定定理及性质定理,并能灵活运用.
对点练
(2022·江西南昌模拟)如图所示,四棱锥S-ABCD中,BC⊥平面SAB,AD⊥平面SAB,△SBC是等腰直角三角形,∠SBA=∠DSA=60°,AD=3BC.
(1)求证:SA⊥平面SBC;
(1)证明 因为AD⊥平面SAB,所以SA⊥AD.
在Rt△SAD中,∠DSA=60°,令DA=6,得BC=2,SA=2 .因为BC⊥平面SAB,且SB,SA 平面SAB,故SA⊥BC,SB⊥BC.因为△SBC是等腰直角三角形,故SB=BC=2.
在△SAB中,SA2=BA2+SB2-2BA·SB·cos∠SBA,
解得BA=4,则BA2=SB2+SA2,即SA⊥SB.
因为SB,BC 平面SBC,SB∩BC=B,
故SA⊥平面SBC.
(2)解 连接BD交AC于点G,连接EG.
因为SB∥平面ACE,平面SBD∩平面ACE=EG,
热点二 与体积和空间距离有关的问题
典例突破2
(2022·云南德宏高三期末)如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,且∠BAP=∠CDP=90°.
(1)证明:平面PAB⊥平面PAD;
(2)若PA⊥PD,PA=PD=2,AB=4,求点D到平面PBC的距离.
(1)证明 ∵∠BAP=∠CDP=90°,∴AB⊥AP,CD⊥PD.
∵AB∥CD,∴AB⊥PD.
∵AP∩PD=P,且AP 平面PAD,PD 平面PAD,∴AB⊥平面PAD.
∵AB 平面PAB,∴平面PAB⊥平面PAD.
(2)解 取线段AD的中点O,连接PO,取线段BC的中点E,连接PE,如图所示.∵PA=PD=2,且PA⊥PD,
∵AB⊥平面PAD,PO 平面PAD,∴AB⊥PO.
∵AB∩AD=A,且AB,AD 平面ABCD,∴PO⊥平面ABCD,即点P到平面
增分技巧
求点到平面距离的常用方法
(1)构造法:根据定义构造垂直于平面的直线,确定垂足的位置,将所求线段化归到三角形中求解.
(2)等积变换法:将所求距离看作某个几何体(多为三棱锥)的高,利用体积相等建立方程求解.
热点三 翻折中的位置关系问题
典例突破3(2022·陕西西安三模)如图1,已知正方形ABCD的边长为4,E,F分别为线段AD,BC的中点,将正方形ABCD沿EF折成如图2所示,且∠DEA=60°,点M在线段AB上(包含端点)运动,连接AD.
图1
图2
(1)若M为AB的中点,直线MF与平面ADE的交点为O,试确定点O的位置,并证明直线OD∥平面EMC;
(2)点H为AE的中点,求证:DH⊥平面ABFE.
(1)解 因为直线MF 平面ABFE,故点O在平面ABFE内,也在平面ADE内,
所以点O在平面ABFE与平面ADE的交线,即直线AE上.
如图所示,延长EA,FM交于点O,连接OD.
因为AO∥BF,M为AB的中点,所以△OAM≌△FBM,所以OM=MF,
连接DF交CE于点N,连接MN,则N为线段DF的中点,所以MN∥OD.又OD 平面EMC,MN 平面EMC,所以OD∥平面EMC.
(2)证明 由已知可得EF⊥AE,EF⊥DE.又EA∩DE=E,且EA,DE 平面ADE,所以EF⊥平面ADE.因为EF 平面ABFE,所以平面ABFE⊥平面ADE.因为∠DEA=60°,DE=AE,所以△ADE为等边三角形,则DH⊥AE.而平面ABFE⊥平面ADE,平面ABFE∩平面ADE=AE,DH 平面ADE,
所以DH⊥平面ABFE.
增分技巧
解决翻折问题的关键是分清翻折前后图形的位置和数量关系的变与不变.一般地,位于“折痕”同侧的点、线、面之间的位置和数量关系不变,而位于“折痕”两侧的点、线、面之间的位置关系会发生变化.对于不变的关系应在平面图形中处理,而对于变化的关系则要在立体图形中解决.
培优拓展
立体几何中的动态、最值问题
立体几何中的“动态问题”是指空间图形中的某些点、线、面的位置是不确定的,是可变的一类开放性问题.因其某些点、线、面位置的不确定,往往成为学生进行常规思考、转化的障碍.主要包括空间中动点的轨迹判断,求轨迹的长度及动角的范围,判断动点、动线、动面的位置关系等.
角度1求动点的轨迹(长度)
【例1】 (2020·山东·16)已知直四棱柱ABCD-A1B1C1D1的棱长均为2,
∠BAD=60°.以D1为球心, 为半径的球面与侧面BCC1B1的交线长为 .
解析 如图所示,
∵∠B1C1D1=∠B1A1D1=∠BAD=60°且B1C1=C1D1,
∴△B1C1D1为等边三角形.
∴B1D1=2.
规律方法
立体几何中空间动点轨迹的判断或求轨迹的长度,一般是根据线、面平行,线、面垂直的判定定理和性质定理,结合圆或圆锥曲线的定义推断出动点的轨迹(还可以利用空间向量的坐标运算求出动点的轨迹方程).
角度2求取值范围或最值问题
【例2】 (1)在空间直角坐标系O-xyz中,正四面体P-ABC的顶点A,B分别在x轴、y轴上移动.若该正四面体的棱长是2,则|OP|的取值范围是( )
答案 (1)A (2)60π
解析 (1)如图所示,若固定正四面体P-ABC的位置,则原点O在以AB为直径的球面上运动,
(2)当三棱锥A-BCD的体积最大时,平面ABD⊥平面BCD,如图,取BD的中点为H,连接AH,CH,则AH⊥BD.
设O1,O2分别为△ABD,△BCD外接圆的圆心,O为
三棱锥A-BCD的外接球的球心,则O1在AH上,O2在CH上,
因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AH 平面ABD,故AH⊥平面BCD,则AH∥O2O.
同理,CH∥O1O,故四边形O1OO2H为平行四边形.
因为AH⊥平面BCD,O2H 平面BCD,故AH⊥O2H,
规律方法
解决与空间图形有关的线段、角、距离、面积、体积等最值问题,一般可以从三方面着手:
一是从问题的几何特征入手,充分利用其几何性质去解决;
二是利用空间几何体的侧面展开图;
三是找出问题中的代数关系,建立目标函数,利用代数方法求目标函数的最值.
培优拓展
立体几何中的截面、交线问题
空间几何体的截面问题是高考命题的热点,它是空间问题转化为平面问题的纽带,也是考查空间想象能力的最佳切入点.确定空间几何体的截面关键是寻找这个平面与几何体表面的交线.
平面截几何体有三种基本方式:横截、纵截和斜截.考查较多的是旋转体的轴截面和正方体中的斜截面.常见的几种截面图如下:
1.正方体的斜截面
方式 横截 竖截 斜截
正六面体 正方形 正方形/矩形 如上图所示
2.圆柱体的基本截面
方式 横截 竖截 斜截
圆柱体 圆形 矩形 如上图③④⑤所示
考点二
确定截面形状
角度1直接法
【例1】 在正方体ABCD-A1B1C1D1中,P为BB1的中点,画出过点A1,C1,P的截面.
解 因为此三点在几何体的棱上,且两两在一个平面内,直接连接A1P,A1C1,C1P就得到截面A1C1P.
增分技巧
若截面上的点都在几何体的棱上,且两两在同一个平面内,可借助基本事实“如果一条直线上的两点在一个平面内,那么这条直线上所有点都在这个平面内”,可直接连线作截面.
角度2平行线法
【例2】 (2022·河南南阳中学三模)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点P是棱AB上的动点,过A1,C1,P三点作正方体的截面,若截面把正方体分成体积之比为7∶25的两部分,则该截面的周长为( )
答案 D
解析 如图所示,过点P作PQ∥A1C1,交BC于点Q,则四边形PQC1A1就是过点A1,C1,P的截面,且PB=BQ.设PB=x(0≤x≤2),则台体PBQ-A1B1C1的体积为
增分技巧
若截面与几何体的两个平行平面相交,或者截面上有一条直线与几何体的某一个表面平行,可以借助于两个性质:(1)如果一条直线平行于一个平面,经过这条直线的平面与这个平面相交,那么这条直线就和交线平行;(2)如果两个平面平行,第三个平面和它们相交,那么两条交线平行,利用平行线法作截面.
角度3延长线法
【例3】 (2022·河南商丘检测)已知正方体ABCD-A1B1C1D1的棱长为3,E为棱BB1上靠近B1的三等分点,则平面AED1截正方体ABCD-A1B1C1D1的截面面积为( )
答案 C
解析 延长AE,A1B1交于点F,连接D1F交B1C1于点G,如图所示.
在正方体ABCD-A1B1C1D1中,平面ADD1A1∥平面BCC1B1.
∵平面AFD1∩平面ADD1A1=AD1,平面AFD1∩平面BCC1B1=EG,∴AD1∥GE.
增分技巧
若截面上的点中至少有两个在一个几何体的一个表面上,可以借助基本事实“如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内”,用作延长线的方法确定平面.
对点练1在正方体ABCD-A1B1C1D1中,M,N分别是线段C1D1,C1C的中点,则平面BMN截正方体所得截面的形状为( )
A.长方形 B.等腰三角形
C.平行四边形 D.等腰梯形
答案 D
解析 连接A1B,A1M,则四边形MNBA1为所求截面,易得A1B∥MN,且
MN= A1B,所以平面BMN截正方体所得截面为
梯形MNBA1.因为M,N分别是线段C1D1,C1C的中点,
所以A1M=BN,故所得截面的形状为等腰梯形.
对点练2(2022·湖北恩施高一期中)在正方体ABCD-A1B1C1D1中,M,N分别是棱DD1和BB1上的点,MD= DD1,NB= BB1,那么正方体中过点M,N,C1的截面图形是( )
A.三角形 B.四边形
C.五边形 D.六边形
答案 C
解析 延长C1M,CD相交于点P,延长C1N,CB相交于点Q,连接PQ交AD于点E,交AB于点F,则五边形C1MEFN为所求截面图形.
对点练3 在正方体ABCD-A1B1C1D1中,F为AD的中点,E为棱D1D上的动点(不包括端点),过点B,E,F的平面截正方体所得的截面的形状不可能是( )
A.四边形 B.等腰梯形
C.五边形 D.六边形
答案 D
解析 不妨设正方体的棱长为1,当0特别地,当DE= 时,截面为等腰梯形BFEC1,如图2;
当考点三
球与多面体的交线问题
【例4】 (2022·山东临沂一模)已知正三棱台ABC-A1B1C1的上、下底面边长分别为2和5,侧棱长为3,则以下底面的一个顶点为球心,半径为2的球面与此正三棱台的表面的交线长为 .
答案 2π
解析 由题意不妨令下底面为△ABC,则△ABC是边长为5的等边三角形,侧面均为全等的等腰梯形,在四边形ABB1A1中,AB=5,A1B1=2,AA1=BB1=3,
在棱AB上取BF=2,连接A1F,易知△AA1F为等边三角形,
即∠A1AB=60°,则以下底面的一个顶点A为球心,
增分技巧
先根据题意分析正三棱台的结构特征,确定该球面和三棱台的交线形状,进而利用弧长公式求其长度.
对点练4(2022·广东广州一模)已知三棱锥P-ABC的棱AP,AB,AC两两互相垂直,AP=AB=AC=2 ,以顶点P为球心,4为半径作一个球,球面与该三棱锥的表面相交得到四段弧,则最长弧的弧长等于 .
解析 由题设,将三棱锥P-ABC补全为棱长为2 的正方体,如图所示.
若AD=AF=2,则PD=PF=4,即点D,F在以P为球心,4为半径的球面上,且O为底面中心.
保分2
空间向量与空间角、距离
热点一 利用空间向量求空间角
考向1直线与平面所成的角
典例突破1(2022·全国乙·理18)如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC的中点.
(1)证明:平面BED⊥平面ACD;
(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.
(1)证明 ∵AD=CD,∠ADB=∠BDC,BD=BD,
∴△ABD≌△CBD,∴AB=CB.又E为AC的中点,AD=CD,∴DE⊥AC,BE⊥AC.又BE∩DE=E,∴AC⊥平面BED.
又AC 平面ACD,∴平面BED⊥平面ACD.
(2)解 如图,连接EF,由(1)知AC⊥平面BED.
∴EF⊥AC,∴当△AFC的面积最小时,EF最小.
在△BDE中,若EF最小,则EF⊥BD.
∵AB=CB=2,∠ACB=60°,∴△ABC为等边三角形,
∴△ACD为等腰直角三角形,∴DE=1.
又BD=2,∴DE2+BE2=BD2,∴BE⊥DE.
由(1)知DE⊥AC,BE⊥AC,则以E为原点,EA,EB,ED所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
增分技巧
利用向量求直线与平面所成角的方法
(1)分别求出直线与它在平面内的射影的方向向量,转化为求两个方向向量的夹角(或其补角).
(2)求出直线的方向向量m,平面的法向量n,设直线与平面所成的角为θ,则sin θ=|cos|= ,求出θ的值.
对点练1
(2022·湖北武汉二模)如图,圆台上底面圆O1半径为1,下底面圆O2半径为 ,AB为圆台下底面的一条直径,圆O2上点C满足AC=BC,PO1是圆台上底面的一条半径,点P,C在平面ABO1的同侧,且PO1∥BC.
(1)证明:平面PAC⊥平面ABC;
(2)若圆台的高为2,求直线AO1与平面PBC所成角的正弦值.
(1)证明 取AC的中点M,
所以四边形PO1O2M为平行四边形,则PM∥O1O2.
又O1O2⊥平面ABC,故PM⊥平面ABC.
又PM 平面PAC,故平面PAC⊥平面ABC.
考向2二面角
典例突破2
(12分)(2021·新高考Ⅱ·19)在四棱锥Q-ABCD中,底面ABCD是正方形,若AD=2,QD=QA= ,QC=3.
(1)证明:平面QAD⊥平面ABCD;
(2)求二面角B-QD-A的平面角的余弦值.
【规范解答】
(2)解:在平面ABCD内,过点O作OT∥CD,交BC于点T,则OT⊥AD,
结合(1)中的QO⊥平面ABCD,
故可建立如图所示的空间直角坐标系,
则D(0,1,0),Q(0,0,2),B(2,-1,0),
【教师讲评】
1.在(1)中,要证明面面垂直,需证明其中一个平面内的一条直线与另一个平面垂直.由条件中的数据可知△QAD为等腰三角形,从结论入手,反向思维,可知在△QAD中构造与AD垂直的线即与另一个平面垂直.
2.求二面角一般利用向量法,关键是建系,准确写出相关点的坐标,并寻找或计算两个平面的法向量,再根据公式计算即可.本题建系时可结合第(1)问的线面垂直及底面为正方形来构建.
增分技巧
利用空间向量求二面角的步骤
(1)分别求出两个半平面的一个法向量;
(2)求出两个法向量的夹角;
(3)根据图形判断二面角的平面角是锐角还是钝角,利用二面角的平面角与两个法向量的夹角的关系,求出二面角.
对点练2(2022·新高考Ⅱ·20)如图,PO是三棱锥P-ABC的高,PA=PB,AB⊥AC,E为PB的中点.
(1)证明:OE∥平面PAC;
(2)若∠ABO=∠CBO=30°,PO=3,PA=5,求二面角C-AE-B的正弦值.
(1)证明 连接OA,OB,如图所示.
∵PO是三棱锥P-ABC的高,∴PO⊥平面ABC,
∴PO⊥OA,PO⊥OB,∠POA=∠POB=90°.
又PA=PB,PO=PO,∴△POA≌△POB,∴OA=OB.
取AB的中点D,连接OD,DE,则OD⊥AB.
∵AB⊥AC,∴OD∥AC.
又AC 平面PAC,OD 平面PAC,∴OD∥平面PAC.
∵D,E分别是AB,PB的中点,∴DE∥PA.
又DE 平面PAC,PA 平面PAC,∴DE∥平面PAC.
∵OD∩DE=D,∴平面ODE∥平面PAC.
∵OE 平面ODE,∴OE∥平面PAC.
(2)解 过点D作DF∥OP,分别以DB,DO,DF所在直线为x轴、y轴、z轴,建立如下图所示的空间直角坐标系.
∵PO=3,PA=5,∴OA=4.
由(1)知OB=OA=4,又∠ABO=∠CBO=30°,
热点二 利用空间向量求距离
典例突破3
(2022·北京东城一模)如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,AB=AC=AA1=1,M为线段A1C1上一点.
(1)求证:BM⊥AB1;
(2)若直线AB1与平面BCM所成角为 ,求点A1到平面BCM的距离.
(1)证明 因为AA1⊥平面ABC,AB,AC 平面ABC,
所以AA1⊥AB,AA1⊥AC,而AB⊥AC,因此建立如图所示的空间直角坐标系,
则A(0,0,0),A1(0,0,1),B(1,0,0),C(0,1,0),B1(1,0,1).设M(0,a,1)(a∈[0,1]),
增分技巧
求点到平面的距离的四步骤
对点练3(2022·山东潍坊二模)如图,线段AC是圆O的直径,点B是圆O上异于A,C的点,AC=2,BC=1,PA⊥底面ABC,M是PB上的动点,且 (0<λ<1),N是线段PC的中点.
解 (1)直线l∥平面PBC,证明如下:
当λ= 时,M是线段PB的中点.因为N是线段PC的中点,所以MN∥BC.又BC 平面ABC,且MN 平面ABC,所以MN∥平面ABC.因为MN 平面AMN,且平面AMN∩平面ABC=l,所以MN∥l.又l 平面PBC,MN 平面PBC,所以直线l∥平面PBC.
(2)因为AC是圆O的直径,所以∠ABC=90°.
又AC=2,BC=1,所以AB= .
因为PA⊥平面ABC,BC 平面ABC,所以PA⊥BC.
又AB⊥BC,AB,BC 平面PBA,AB∩PA=A,
所以BC⊥平面PBA,而PB 平面PBA,故PB⊥BC,
以点B为坐标原点,BA,BC所在直线分别为x轴、y轴建立如图所示的空间直角坐标系,
热点三 空间中的探索性问题
考向1位置关系中的探索性问题
典例突破4
(2022·广东江门模拟)如图,在正四棱锥S-ABCD中,AC∩BD=O,SA= AB,P在侧棱SD上,SD⊥平面PAC.
(1)求平面SAB与平面PAC所成的二面角的余弦值;
(2)侧棱SC上是否存在一点E,使得BE∥平面PAC
若存在,求SE∶EC的值;若不存在,请说明理由.
解 (1)如图,由题意知SO⊥平面ABCD,AC⊥BD,故OS,OB,OC两两垂直.
增分技巧
立体几何中探索性问题的求解策略
(1)探索性问题的一般解法:
①可先猜后证,即先观察并尝试给出条件再证明.
②首先假设结论成立,然后把这个假设作为已知条件,与题目的其他已知条件一起进行推理论证和计算.在推理论证和计算无误的前提下,若得到一个合理的结论,则说明假设成立;若得到一个不合理的结论,则说明假设不成立.
(2)涉及在线段上是否存在符合某条件的点的问题,可以先根据条件猜测点的位置,特别注意特殊位置关系和极端情形的应用.
(3)可借助空间直角坐标系将动点用坐标(含参数)表示出来,然后根据已知条件建立关于参数的方程(组),由此解决探索性问题.
对点练4
(2022·江苏苏锡常镇二模)如图,在四棱锥S-ABCD中,已知四边形ABCD为菱形,∠BAD=60°,△SAD为正三角形,平面SAD⊥平面ABCD.
(1)求二面角S-BC-A的大小;
(2)在线段SC上是否存在一点M(端点S,C除外),使得AM⊥BD 若存在,指出点M的位置;若不存在,请说明理由.
解 (1)取AD中点O,连接SO,BO.因为SA=SD,OA=OD,所以SO⊥AD,即SO⊥OA.又因为平面SAD⊥平面ABCD,平面SAD∩平面ABCD=AD,SO 平面SAD,则SO⊥平面ABCD.因为OB 平面ABCD,所以SO⊥OB.
因为BA=BD,OA=OD,所以AO⊥OB,
所以OA,OB,OS两两垂直.
以O为坐标原点建立如图所示空间直角坐标系,设AD=2,则
考向2与空间角有关的探索性问题
典例突破5
(2022·山东德州二模)在《九章算术·商功》中提到的“阳马”这一几何体,是指底面为矩形,有一条侧棱垂直于底面的四棱锥,现有“阳马”P-ABCD,底面为边长为2的正方形,侧棱PA⊥平面ABCD,PA=2,E,F为边BC,CD上的点,
(2)是否存在实数λ(0<λ<1),使二面角P-EF-A的大小为45° 如果不存在,请说明理由;如果存在,求此时直线BM与平面PEF所成角的正弦值.
(1)证明 当λ= 时,点E,F为线段BC,CD的中点.连接AF与BM交于点G,
在△ABM和△DAF中,AB=AD,AM=DF,∠BAM=∠ADF=90°,所以△ABM≌△DAF,故∠ABM=∠FAD.而∠FAD+∠BAF=90°,所以∠ABM+∠BAF=90°,故∠AGB=90°,即BM⊥AF.又PA⊥平面ABCD,BM 平面ABCD,所以PA⊥BM.又PA,AF 平面PAF,PA∩AF=A,所以BM⊥平面PAF.又因为BM 平面PBM,所以平面PBM⊥平面PAF.
(2)解 存在.连接AC交EF于点Q,连接PQ,BD与AC交于点O,如图所示.
所以AC⊥EF.
因为PA⊥平面ABCD,EF 平面ABCD,则PA⊥EF,
而PA,AC 平面PAC,PA∩AC=A,故EF⊥平面PAC.
因为PQ 平面PAC,则PQ⊥EF,
所以∠AQP为二面角P-EF-A的一个平面角.
增分技巧
与空间向量有关的探索性问题主要有两类:一类是探究线面的位置关系;另一类是探究线面角或二面角满足特定要求时的存在性问题.处理原则是:先建立空间直角坐标系,引入参数(有些是题中已给出),设出关键点的坐标,然后探究这样的点是否存在,或参数是否满足要求,从而作出判断.
对点练5
(2022·湖南师大附中二模)在三棱柱ABC-A1B1C1中,四边形AA1B1B是菱形,AB⊥AC,平面AA1B1B⊥平面ABC,平面A1B1C1与平面AB1C的交线为l.
(1)证明:A1B⊥B1C;
(2)若∠ABB1=60°,AB=AC=2,直线l上是否存在点P,
使得A1B与平面ABP所成角为60° 若存在,求B1P的
长度;若不存在,请说明理由.
(1)证明 因为四边形AA1B1B为菱形,所以A1B⊥AB1.因为平面AA1B1B⊥平面ABC,平面AA1B1B∩平面ABC=AB,AC 平面ABC,AC⊥AB,所以AC⊥平面AA1B1B.
又A1B 平面AA1B1B,所以AC⊥A1B.
又AB1,AC 平面B1AC,AB1∩AC=A,所以A1B⊥平面B1AC.又B1C 平面B1AC,所以A1B⊥B1C.
(2)解 直线l上不存在点P,使A1B与平面ABP所成角为60°.理由如下:
取线段A1B1中点D,连接AD.
因为∠ABB1=60°,所以∠AA1B1=60°.又AA1=A1B1,所以△AA1B1为等边三角形,所以AD⊥A1B1.
因为A1B1∥AB,所以AD⊥AB.
因为平面AA1B1B⊥平面ABC,平面AA1B1B∩平面ABC=AB,AD 平面AA1B1B,所以AD⊥平面ABC.
因为AC∥A1C1,AC 平面A1B1C1,A1C1 平面A1B1C1,所以AC∥平面A1B1C1.又因为AC 平面AB1C,平面A1B1C1∩平面AB1C=l,所以AC∥l.
假设l上存在一点P,使A1B与平面ABP所成角为60°.
专题三 立体几何
上篇
2023
内容索引
01
02
03
高考小题突破4 空间几何体的结构、表面积与体积
◎高考保分大题三 立体几何中的证明与计算
培优拓展 立体几何中的动态、最值问题
04
培优拓展 立体几何中的截面、交线问题
考情分析 1.从题型和题量上看,高考对本专题考查基本稳定在“两小一大”的方式,总分约22分.
2.从考查内容上看,小题主要考查空间几何体的结构特征、体积与表面积、球与几何体的“切”“接”、空间位置关系的判断等,难度中等或中低等.解答题多以几何体为载体,考查空间位置关系的证明、空间角的求解等,难度中等.
3.核心素养:直观想象、逻辑推理、数学运算等.
备考策略 1.掌握特殊几何体的结构特征,熟记体积与表面积公式,理解并会应用空间平行与垂直的相关定理与结论,这是解决立体几何问题的基础.
2.注意对空间想象核心素养的训练,通过动手画图,观察分析图形,对空间几何体中位置关系的证明与应用等,都可以有效提升空间想象能力.
3.重视图形的作用,解立体几何问题,可将题目已知或隐含的条件标注在图形上,达到只通过图形就能表述出题目的已知与所求的效果.
4.归纳几何体中常见的建系方法与技巧,并能合理运用.
5.通过题目的训练,提升运算正确率,尤其是利用空间向量求解空间角的问题.
真题感悟
A.100π B.128π
C.144π D.192π
答案 A
解析 设外接球的半径为R,由题意得,上底面所在平面截球所得圆的半径是3,下底面所在平面截球所得圆的半径是4,在轴截面中,设球心到上下底面
2.(2021·全国乙·理5)在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为( )
答案 D
解析 如图,连接BC1,PC1.
3.(2020·全国Ⅰ·理10)已知A,B,C为球O的球面上的三个点,☉O1为△ABC的外接圆.若☉O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为( )
A.64π B.48π
C.36π D.32π
答案 A
4.(2021·全国甲·文14)已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为 .
答案 39π
5.(2020·海南·13)已知正方体ABCD-A1B1C1D1的棱长为2,M,N分别为棱BB1,AB的中点,则三棱锥A-NMD1的体积为 .
6. (2022·全国甲·理18)在四棱锥P-ABCD中,PD⊥底面ABCD,
CD∥AB,AD=DC=CB=1,AB=2,DP= .
(1)证明:BD⊥PA;
(2)求PD与平面PAB所成的角的正弦值.
(1)证明 ∵PD⊥平面ABCD,BD 平面ABCD,∴PD⊥BD.取AB的中点E,连接DE.
∵CD=1,BE= AB=1,CD∥BE,
∴四边形CDEB是平行四边形,∴DE=CB=1.
∵DE= AB,∴△ABD为直角三角形,AB为斜边,
∴BD⊥AD.
∵PD 平面PAD,AD 平面PAD,且PD∩AD=D,
∴BD⊥平面PAD.又PA 平面PAD,∴BD⊥PA.
(2)解 由(1)知,PD,AD,BD两两垂直,以点D为坐标原点,DA,DB,DP所在直线分别为x轴、y轴、z轴建立如图所示空间直角坐标系,其中
7. (2022·新高考Ⅰ·19)如图,直三棱柱ABC-A1B1C1的体积为4,△A1BC的面
(1)求A到平面A1BC的距离;
(2)设D为A1C的中点,AA1=AB,平面A1BC⊥平面ABB1A1,求二面角A-BD-C的正弦值.
∵AA1=AB,∴AB1⊥A1B.又平面A1BC⊥平面ABB1A1,平面A1BC∩平面ABB1A1=A1B,∴AB1⊥平面A1BC.
又BC 平面A1BC,∴BC⊥AB1,又BC⊥BB1,AB1,BB1 平面ABB1A1,且AB1∩BB1=B1,
∴BC⊥平面ABB1A1,∴BC⊥AB,BC⊥A1B.
h=BC=2.
∴点A(0,2,0),B(0,0,0),D(1,1,1),E(0,1,1).
设n1=(x1,y1,z1)为平面ABD的一个法向量.
知识精要
1.空间几何体的表面积与体积公式
球的表面积的大小恰好是球的大圆面积大小的4倍
名师点析
1.圆柱、圆锥、圆台的体积公式之间的关系
2.柱体、锥体、台体的体积公式之间的关系
2.线面、面面平行的判定及性质定理
①线面平行的判定定理:a α,b α,a∥b a∥α;
②线面平行的性质定理:a∥α,a β,α∩β=b a∥b;
③面面平行的判定定理:a α,b α,a∥β,b∥β,a∩b=P α∥β;
④面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b a∥b.
3.线面、面面垂直的判定及性质定理
①线面垂直的判定定理:m α,n α,m∩n=P,l⊥m,l⊥n l⊥α;
②线面垂直的性质定理:a⊥α,b⊥α a∥b;
③面面垂直的判定定理:a β,a⊥α β⊥α;
④面面垂直的性质定理:α⊥β,α∩β=l,a α,a⊥l a⊥β.
4.利用空间向量求空间角
(1)两条异面直线所成的角:设异面直线l,m的方向向量分别为a,b,且它们所
公式两边都有绝对值,所以两角相等或互补
名师点析
利用空间向量求空间角时,一定要注意角的取值范围.对于二面角,要注意题目条件是
否明确是锐角还是钝角,如果没有说明,则结合图形特点判断.若求两个不平行平面的夹角,则取直角或锐角.
5.利用空间向量求点到平面的距离
如图所示,已知AB为平面α的一条斜线段,n为平面α的法向量,则点B到平面
常用结论
2.空间几何体中的常用结论
(1)若长方体从一个顶点出发的三条棱长分别为a,b,c,则其外接球的直径为
(2)正四面体(棱长都为a)的几个结论:
正四面体是特殊的正三棱锥,正三棱锥不一定是正四面体
(3)正方体与球的几个结论:
高考小题突破4
考点一
空间几何体的结构特征
(2)(2020·全国Ⅰ·理3)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
答案 (1)B (2)C
解析 (1)设圆锥底面半径为r1,圆锥侧面展开图半圆所在圆的半径为r2.
图①
图②
增分技巧
几何体的表面展开及其应用
(1)圆锥、圆柱的侧面展开图分别为扇形
和矩形,圆锥、圆柱的底面周长分别为扇形的弧长、矩形的一边长,据此建立圆锥、圆柱基本量的联系解决问题.
(2)解决多面体或旋转体的表面上与长度有关的最值问题时,一般采用转化法,即将表面展开化为平面图形,通过“化折为直”或“化曲为直”来解决,注意展开前后哪些几何量发生变化,哪些不变.
(2)(2022·河北秦皇岛二模)在长方体ABCD-A1B1C1D1中,AB=2,AD=3,
A1A=1,P为线段C1D1的中点,一质点从A点出发,沿长方体表面运动到达P点处,则质点从A到P的最短距离为 ;若沿质点A的最短运动路线截长方体,则所得截面的面积为 .
图1
图2
图3
此时质点从A点出发,经过A1D1的中点E,再到达P点,则平面AEP截长方体所得的截面为梯形ACPE,如图5所示,
图4
图5
考点二
空间几何体的表面积与体积
考向1空间几何体的表面积
典例突破2(1)(多选)(2022·湖北武汉模拟)一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R相等,下列结论正确的是( )
A.圆柱的侧面积为4πR2
B.圆锥的侧面积为2πR2
C.圆柱的侧面积与球的表面积相等
D.球的体积是圆锥体积的两倍
(2)(2022·辽宁锦州一模)“水立方”的设计灵感来自威尔·弗兰泡沫,威尔·弗兰泡沫是对开尔文胞体的改进,开尔文胞体是一种多面体,它由正六边形和正方形围成(其中每一个顶点处有一个正方形和两个正六边形),已知该多面体共有24个顶点,且棱长为2,则该多面体的表面积是( )
答案 (1)ACD (2)C
解析 (1)对于A,∵圆柱的底面直径和高都等于2R,∴圆柱的侧面积S1=2πR·2R=4πR2.故A正确;对于B,∵圆锥的底面直径和高等于2R,
(2)由题得,棱长为2的正方形的面积为2×2=4,正六边形的面积为
24个顶点,所以最多有6个正方形,最少有4个正六边形,1个正六边形与3个正方形相连,所以该多面体有6个正方形,则正六边形有6×4÷3=8(个).
增分技巧
空间几何体表面积的求法
(1)求表面积问题的思路是将立体几何问题转化为平面几何问题,即空间图形平面化,这是解决立体几何问题的主要出发点.
(2)求不规则几何体的表面积时,通常将所给几何体分割成柱体、锥体、台体,先求出这些柱体、锥体、台体的表面积,再通过求和或作差求得所给几何体的表面积.
对点练2
(1)(2022·福建福州模拟)如图,一个正六棱柱的茶叶盒,底面边长为10 cm,高为20 cm,则这个茶叶盒的表面积约为 cm2.(精确到0.1, ≈1.732)
(2)(2022·广东惠州一模)若一个圆台的侧面展开图是半圆面所在的扇环,且扇环的面积为4π,圆台上、下底面圆的半径分别为r1,r2(r1
200+300×1.732=1 719.6(cm2).
(2)因为圆台的侧面展开图是半圆面所在的扇环,所以圆台的母线长为
考向2空间几何体的体积
典例突破3(1)(2022·新高考Ⅰ·4)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5 m时,相应水面的面积为140.0 km2;水位为海拔157.5 m时,相应水面的面积为180.0 km2.将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5 m上升到157.5 m时,增加的水量约为( ≈2.65)( )
A.1.0×109 m3 B.1.2×109 m3
C.1.4×109 m3 D.1.6×109 m3
(2)(2021·北京·8)某一时间段内,从天空降落到地面上的雨水,未经蒸发、渗漏、流失而在水平面上积聚的深度,称为这个时段的降雨量(单位:mm).24 h降雨量的等级划分如下:
等级 24 h降雨量(精确到0.1)
…… ……
小雨 0.1~9.9
中雨 10.0~24.9
大雨 25.0~49.9
暴雨 50.0~99.9
…… ……
在综合实践活动中,某小组自制了一个底面直径为200 mm,高为300 mm的圆锥形雨量器.若一次降雨过程中,该雨量器收集的24 h的雨水高度是150 mm(如图所示),则这24 h降雨量的等级是( )
A.小雨 B.中雨
C.大雨 D.暴雨
答案 (1)C (2)B
解析 (1)由题意可得,此棱台的高h=157.5-148.5=9(m).
设水库水位为海拔148.5 m时,相应水面的面积为S1,水库水位为海拔157.5 m时,相应水面的面积为S2,则S1=140.0 km2=1.4×108 m2,S2=180.0 km2
即增加的水量约为1.4×109 m3.故选C.
增分技巧
求几何体体积的基本方法
(1)直接法:对于规则的几何体,可利用相关公式直接计算求解.
(2)割补法:对于不规则的几何体,可将其分割成规则的几何体,进行体积计算;也可把不规则的几何体补成规则的几何体,进行体积计算.
(3)转换法:主要用于求三棱锥(四面体)的体积,将三棱锥的顶点和底面进行转换,使其底面的面积可求(或容易求),高可求(或容易求),从而代入公式求得体积.
对点练3(1)某品牌暖水瓶的内胆规格如图所示,分为①②③④四个部分(水瓶内胆壁厚不计),它们分别为一个半球、一个大圆柱、一个圆台和一个小圆柱.若其中圆台部分的体积为52π cm3,且水瓶灌满水后盖上瓶塞时水溢
(2)(2019·全国Ⅲ·16)学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm.3D打印所用原料密度为0.9 g/cm3.不考虑打印损耗,制作该模型所需原料的质量为 g.
答案 (1)A (2)118.8
ABCD-A1B1C1D1的体积为V2=4×6×6=144(cm3),
则该模型的体积为V=V2-V1=144-12=132(cm3).故其质量为0.9×132=118.8(g).
考点三
球的“切”“接”问题
考向1外接球问题
典例突破4(1)(2021·天津·6)两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为 ,两个圆锥的高之比为1∶3,则这两个圆锥的体积之和为( )
A.3π B.4π C.9π D.12π
(2)(2022·山东聊城一模)“阿基米德多面体”也称半正多面体,是由边数不全相同的正多边形围成的多面体.如图是以一正方体的各条棱的中点为顶点的多面体,这是一个有八个面为正三角形,六个面为正方形的“阿基米德多面体”,若该多面体的棱长为1,则经过该多面体的各个顶点的球的体积为( )
答案 (1)B (2)A
所以AB=AD+BD=4BD=4,
所以BD=1,AD=3.设两个圆锥的公共底面圆的半径为r,
增分技巧
解决几何体外接球问题的基本方法
(1)由球的定义确定球心.
①正方体或长方体的外接球的球心是其体对角线的中点.
②正棱柱的外接球的球心是上、下底面中心的连线的中点.
③直三棱柱的外接球的球心是上、下底面三角形外心的连线的中点.
④正棱锥的外接球的球心在其高上,具体位置可通过构造直角三角形,利用勾股定理求得.
(2)构造正方体或长方体确定球心.
①可构造正方体的情况:a.正四面体,其棱长对应正方体的面对角线长;b.三条侧棱两两垂直的正三棱锥,其底面边长对应正方体的面对角线长,侧棱长对应正方体的棱长.
②可构造长方体的情况:a.某一个顶点处的三条棱两两垂直的四面体;b.四个面都是直角三角形的三棱锥;c.相对的棱相等的三棱锥.
(3)利用性质确定球心.
对点练4
(1)(2022·广东佛山二模)如图,某几何体由共底面的圆锥和圆柱组合而成,且圆柱的两个底面和圆锥的顶点均在体积为36π的球面上,若圆柱的高为2,则圆锥的侧面积为( )
(2)(2022·湖南长沙高三调研)蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗产名录.已知某鞠的表面上有五个点P,A,B,C,D恰好构成一正四棱锥P-ABCD,若该棱锥的高为8,底面边长为4 ,则该鞠的表面积为( )
A.64π B.100π C.132π D.144π
答案 (1)B (2)B
解析 (1)依题意,作球的剖面图,其中O是球心,E是圆锥的顶点,EC是圆锥的母线.设球的半径为R,则 πR3=36π,解得R=3.
(2)依题意作图,∵P-ABCD是正四棱锥,
∴底面ABCD是正方形,且点P在底面的投影为正方形ABCD的中心O1,则PO1⊥平面ABCD.
∵外接球的球心在PO1上,设球心为O,连接BO,则BO为外接球的半径R.又PO1=8,PO=R,∴在Rt△BOO1中,BO2=(8-PO)2+B,即R2=(8-R)2+42,解得R=5,故外接球的表面积S=4πR2=100π.
考向2内切球问题
典例突破5(1)(2020·全国Ⅲ·文16)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为 .
(2)(2022·广东二模)如图,该十字贯穿体由两个全等的正四棱柱组合而成,且两个四棱柱的侧棱互相垂直,若底面正方形边长为2,则这两个正四棱柱公共部分所构成的几何体的内切球的体积为 .
解析 (1)(方法一)由题意可知该圆锥的轴截面为底边长为2,腰长为3的等腰三角形,其内切圆为该球的大圆.如图,SB=3,BC=1,
设该球内切于母线SB,切点为点O.
(方法二)由题意可知该圆锥的轴截面为底边长为2,腰长为3的等腰三角形,其内切圆为该球的大圆.
(2)如图所示,这两个正四棱柱公共部分所构成的几何体为两个全等的四棱锥S-ABCD和P-ABCD.
由题意,这两个直四棱柱的中心既是外接球的球心,也是
内切球的球心,设内切球的半径为R,线段AC的中点为H,
连接BH,SH,可知SH即为四棱锥S-ABCD的高.
增分技巧
求几何体内切球的半径的常用方法
(1)将空间问题转化为平面问题,通过构造直角三角形,利用平面知识求出内切球的半径.
(2)利用体积分割求出内切球的半径.
对点练5(1)(2022·湖南长郡中学模拟)如图,球与圆柱的侧面及上、下底面相切,设圆柱的体积与球的体积之比为m,圆柱的表面积与球的表面积之比
(2)(2022·山东烟台一模)如图,在三棱锥V-ABC中,VA⊥底面ABC,
∠BAC=90°,AB=AC=AV=2,则该三棱锥的内切球和外接球的半径之比为( )
答案 (1)B (2)C
解析 (1)设球的半径为R,则圆柱的底面圆的半径为R,高为2R,则圆柱的体积
(2)因为VA⊥底面ABC,AB,AC 底面ABC,所以VA⊥AB,VA⊥AC.因为∠BAC=90°,所以AB⊥AC,而AB=AC=AV=2,因为三条互相垂直且共顶点的棱,可以看成正方体中共顶点的三条棱,因此该三棱锥外接球的半径
高考保分大题三
保分1
空间中的平行与垂直
热点一 空间平行、垂直关系的证明与应用
典例突破1
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD= AD,E,F分别为线段PC,BD的中点.
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PDC.
证明 (1)连接AC,AC∩BD=F.因为四边形ABCD为正方形,F为线段AC中点,E为线段PC中点,所以在△CPA中,EF∥PA.
因为PA 平面PAD,EF 平面PAD,
所以EF∥平面PAD.
(2)在正方形ABCD中,CD⊥AD.
因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD 平面ABCD,所以CD⊥平面PAD,所以CD⊥PA.
又PA=PD= AD,所以△PAD是等腰直角三角形,且∠APD=90°,即PA⊥PD.因为CD∩PD=D,且CD,PD 平面PDC,所以PA⊥平面PDC.
又PA 平面PAB,所以平面PAB⊥平面PDC.
增分技巧
空间几何体中线面位置关系的判断方法
(1)明确空间几何体的结构特征,明确其中已有的平行、垂直关系.
(2)熟练掌握线面平行、面面平行、线面垂直、面面垂直的判定定理及性质定理,并能灵活运用.
对点练
(2022·江西南昌模拟)如图所示,四棱锥S-ABCD中,BC⊥平面SAB,AD⊥平面SAB,△SBC是等腰直角三角形,∠SBA=∠DSA=60°,AD=3BC.
(1)求证:SA⊥平面SBC;
(1)证明 因为AD⊥平面SAB,所以SA⊥AD.
在Rt△SAD中,∠DSA=60°,令DA=6,得BC=2,SA=2 .因为BC⊥平面SAB,且SB,SA 平面SAB,故SA⊥BC,SB⊥BC.因为△SBC是等腰直角三角形,故SB=BC=2.
在△SAB中,SA2=BA2+SB2-2BA·SB·cos∠SBA,
解得BA=4,则BA2=SB2+SA2,即SA⊥SB.
因为SB,BC 平面SBC,SB∩BC=B,
故SA⊥平面SBC.
(2)解 连接BD交AC于点G,连接EG.
因为SB∥平面ACE,平面SBD∩平面ACE=EG,
热点二 与体积和空间距离有关的问题
典例突破2
(2022·云南德宏高三期末)如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,且∠BAP=∠CDP=90°.
(1)证明:平面PAB⊥平面PAD;
(2)若PA⊥PD,PA=PD=2,AB=4,求点D到平面PBC的距离.
(1)证明 ∵∠BAP=∠CDP=90°,∴AB⊥AP,CD⊥PD.
∵AB∥CD,∴AB⊥PD.
∵AP∩PD=P,且AP 平面PAD,PD 平面PAD,∴AB⊥平面PAD.
∵AB 平面PAB,∴平面PAB⊥平面PAD.
(2)解 取线段AD的中点O,连接PO,取线段BC的中点E,连接PE,如图所示.∵PA=PD=2,且PA⊥PD,
∵AB⊥平面PAD,PO 平面PAD,∴AB⊥PO.
∵AB∩AD=A,且AB,AD 平面ABCD,∴PO⊥平面ABCD,即点P到平面
增分技巧
求点到平面距离的常用方法
(1)构造法:根据定义构造垂直于平面的直线,确定垂足的位置,将所求线段化归到三角形中求解.
(2)等积变换法:将所求距离看作某个几何体(多为三棱锥)的高,利用体积相等建立方程求解.
热点三 翻折中的位置关系问题
典例突破3(2022·陕西西安三模)如图1,已知正方形ABCD的边长为4,E,F分别为线段AD,BC的中点,将正方形ABCD沿EF折成如图2所示,且∠DEA=60°,点M在线段AB上(包含端点)运动,连接AD.
图1
图2
(1)若M为AB的中点,直线MF与平面ADE的交点为O,试确定点O的位置,并证明直线OD∥平面EMC;
(2)点H为AE的中点,求证:DH⊥平面ABFE.
(1)解 因为直线MF 平面ABFE,故点O在平面ABFE内,也在平面ADE内,
所以点O在平面ABFE与平面ADE的交线,即直线AE上.
如图所示,延长EA,FM交于点O,连接OD.
因为AO∥BF,M为AB的中点,所以△OAM≌△FBM,所以OM=MF,
连接DF交CE于点N,连接MN,则N为线段DF的中点,所以MN∥OD.又OD 平面EMC,MN 平面EMC,所以OD∥平面EMC.
(2)证明 由已知可得EF⊥AE,EF⊥DE.又EA∩DE=E,且EA,DE 平面ADE,所以EF⊥平面ADE.因为EF 平面ABFE,所以平面ABFE⊥平面ADE.因为∠DEA=60°,DE=AE,所以△ADE为等边三角形,则DH⊥AE.而平面ABFE⊥平面ADE,平面ABFE∩平面ADE=AE,DH 平面ADE,
所以DH⊥平面ABFE.
增分技巧
解决翻折问题的关键是分清翻折前后图形的位置和数量关系的变与不变.一般地,位于“折痕”同侧的点、线、面之间的位置和数量关系不变,而位于“折痕”两侧的点、线、面之间的位置关系会发生变化.对于不变的关系应在平面图形中处理,而对于变化的关系则要在立体图形中解决.
培优拓展
立体几何中的动态、最值问题
立体几何中的“动态问题”是指空间图形中的某些点、线、面的位置是不确定的,是可变的一类开放性问题.因其某些点、线、面位置的不确定,往往成为学生进行常规思考、转化的障碍.主要包括空间中动点的轨迹判断,求轨迹的长度及动角的范围,判断动点、动线、动面的位置关系等.
角度1求动点的轨迹(长度)
【例1】 (2020·山东·16)已知直四棱柱ABCD-A1B1C1D1的棱长均为2,
∠BAD=60°.以D1为球心, 为半径的球面与侧面BCC1B1的交线长为 .
解析 如图所示,
∵∠B1C1D1=∠B1A1D1=∠BAD=60°且B1C1=C1D1,
∴△B1C1D1为等边三角形.
∴B1D1=2.
规律方法
立体几何中空间动点轨迹的判断或求轨迹的长度,一般是根据线、面平行,线、面垂直的判定定理和性质定理,结合圆或圆锥曲线的定义推断出动点的轨迹(还可以利用空间向量的坐标运算求出动点的轨迹方程).
角度2求取值范围或最值问题
【例2】 (1)在空间直角坐标系O-xyz中,正四面体P-ABC的顶点A,B分别在x轴、y轴上移动.若该正四面体的棱长是2,则|OP|的取值范围是( )
答案 (1)A (2)60π
解析 (1)如图所示,若固定正四面体P-ABC的位置,则原点O在以AB为直径的球面上运动,
(2)当三棱锥A-BCD的体积最大时,平面ABD⊥平面BCD,如图,取BD的中点为H,连接AH,CH,则AH⊥BD.
设O1,O2分别为△ABD,△BCD外接圆的圆心,O为
三棱锥A-BCD的外接球的球心,则O1在AH上,O2在CH上,
因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AH 平面ABD,故AH⊥平面BCD,则AH∥O2O.
同理,CH∥O1O,故四边形O1OO2H为平行四边形.
因为AH⊥平面BCD,O2H 平面BCD,故AH⊥O2H,
规律方法
解决与空间图形有关的线段、角、距离、面积、体积等最值问题,一般可以从三方面着手:
一是从问题的几何特征入手,充分利用其几何性质去解决;
二是利用空间几何体的侧面展开图;
三是找出问题中的代数关系,建立目标函数,利用代数方法求目标函数的最值.
培优拓展
立体几何中的截面、交线问题
空间几何体的截面问题是高考命题的热点,它是空间问题转化为平面问题的纽带,也是考查空间想象能力的最佳切入点.确定空间几何体的截面关键是寻找这个平面与几何体表面的交线.
平面截几何体有三种基本方式:横截、纵截和斜截.考查较多的是旋转体的轴截面和正方体中的斜截面.常见的几种截面图如下:
1.正方体的斜截面
方式 横截 竖截 斜截
正六面体 正方形 正方形/矩形 如上图所示
2.圆柱体的基本截面
方式 横截 竖截 斜截
圆柱体 圆形 矩形 如上图③④⑤所示
考点二
确定截面形状
角度1直接法
【例1】 在正方体ABCD-A1B1C1D1中,P为BB1的中点,画出过点A1,C1,P的截面.
解 因为此三点在几何体的棱上,且两两在一个平面内,直接连接A1P,A1C1,C1P就得到截面A1C1P.
增分技巧
若截面上的点都在几何体的棱上,且两两在同一个平面内,可借助基本事实“如果一条直线上的两点在一个平面内,那么这条直线上所有点都在这个平面内”,可直接连线作截面.
角度2平行线法
【例2】 (2022·河南南阳中学三模)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点P是棱AB上的动点,过A1,C1,P三点作正方体的截面,若截面把正方体分成体积之比为7∶25的两部分,则该截面的周长为( )
答案 D
解析 如图所示,过点P作PQ∥A1C1,交BC于点Q,则四边形PQC1A1就是过点A1,C1,P的截面,且PB=BQ.设PB=x(0≤x≤2),则台体PBQ-A1B1C1的体积为
增分技巧
若截面与几何体的两个平行平面相交,或者截面上有一条直线与几何体的某一个表面平行,可以借助于两个性质:(1)如果一条直线平行于一个平面,经过这条直线的平面与这个平面相交,那么这条直线就和交线平行;(2)如果两个平面平行,第三个平面和它们相交,那么两条交线平行,利用平行线法作截面.
角度3延长线法
【例3】 (2022·河南商丘检测)已知正方体ABCD-A1B1C1D1的棱长为3,E为棱BB1上靠近B1的三等分点,则平面AED1截正方体ABCD-A1B1C1D1的截面面积为( )
答案 C
解析 延长AE,A1B1交于点F,连接D1F交B1C1于点G,如图所示.
在正方体ABCD-A1B1C1D1中,平面ADD1A1∥平面BCC1B1.
∵平面AFD1∩平面ADD1A1=AD1,平面AFD1∩平面BCC1B1=EG,∴AD1∥GE.
增分技巧
若截面上的点中至少有两个在一个几何体的一个表面上,可以借助基本事实“如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内”,用作延长线的方法确定平面.
对点练1在正方体ABCD-A1B1C1D1中,M,N分别是线段C1D1,C1C的中点,则平面BMN截正方体所得截面的形状为( )
A.长方形 B.等腰三角形
C.平行四边形 D.等腰梯形
答案 D
解析 连接A1B,A1M,则四边形MNBA1为所求截面,易得A1B∥MN,且
MN= A1B,所以平面BMN截正方体所得截面为
梯形MNBA1.因为M,N分别是线段C1D1,C1C的中点,
所以A1M=BN,故所得截面的形状为等腰梯形.
对点练2(2022·湖北恩施高一期中)在正方体ABCD-A1B1C1D1中,M,N分别是棱DD1和BB1上的点,MD= DD1,NB= BB1,那么正方体中过点M,N,C1的截面图形是( )
A.三角形 B.四边形
C.五边形 D.六边形
答案 C
解析 延长C1M,CD相交于点P,延长C1N,CB相交于点Q,连接PQ交AD于点E,交AB于点F,则五边形C1MEFN为所求截面图形.
对点练3 在正方体ABCD-A1B1C1D1中,F为AD的中点,E为棱D1D上的动点(不包括端点),过点B,E,F的平面截正方体所得的截面的形状不可能是( )
A.四边形 B.等腰梯形
C.五边形 D.六边形
答案 D
解析 不妨设正方体的棱长为1,当0
当
球与多面体的交线问题
【例4】 (2022·山东临沂一模)已知正三棱台ABC-A1B1C1的上、下底面边长分别为2和5,侧棱长为3,则以下底面的一个顶点为球心,半径为2的球面与此正三棱台的表面的交线长为 .
答案 2π
解析 由题意不妨令下底面为△ABC,则△ABC是边长为5的等边三角形,侧面均为全等的等腰梯形,在四边形ABB1A1中,AB=5,A1B1=2,AA1=BB1=3,
在棱AB上取BF=2,连接A1F,易知△AA1F为等边三角形,
即∠A1AB=60°,则以下底面的一个顶点A为球心,
增分技巧
先根据题意分析正三棱台的结构特征,确定该球面和三棱台的交线形状,进而利用弧长公式求其长度.
对点练4(2022·广东广州一模)已知三棱锥P-ABC的棱AP,AB,AC两两互相垂直,AP=AB=AC=2 ,以顶点P为球心,4为半径作一个球,球面与该三棱锥的表面相交得到四段弧,则最长弧的弧长等于 .
解析 由题设,将三棱锥P-ABC补全为棱长为2 的正方体,如图所示.
若AD=AF=2,则PD=PF=4,即点D,F在以P为球心,4为半径的球面上,且O为底面中心.
保分2
空间向量与空间角、距离
热点一 利用空间向量求空间角
考向1直线与平面所成的角
典例突破1(2022·全国乙·理18)如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC的中点.
(1)证明:平面BED⊥平面ACD;
(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.
(1)证明 ∵AD=CD,∠ADB=∠BDC,BD=BD,
∴△ABD≌△CBD,∴AB=CB.又E为AC的中点,AD=CD,∴DE⊥AC,BE⊥AC.又BE∩DE=E,∴AC⊥平面BED.
又AC 平面ACD,∴平面BED⊥平面ACD.
(2)解 如图,连接EF,由(1)知AC⊥平面BED.
∴EF⊥AC,∴当△AFC的面积最小时,EF最小.
在△BDE中,若EF最小,则EF⊥BD.
∵AB=CB=2,∠ACB=60°,∴△ABC为等边三角形,
∴△ACD为等腰直角三角形,∴DE=1.
又BD=2,∴DE2+BE2=BD2,∴BE⊥DE.
由(1)知DE⊥AC,BE⊥AC,则以E为原点,EA,EB,ED所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
增分技巧
利用向量求直线与平面所成角的方法
(1)分别求出直线与它在平面内的射影的方向向量,转化为求两个方向向量的夹角(或其补角).
(2)求出直线的方向向量m,平面的法向量n,设直线与平面所成的角为θ,则sin θ=|cos
对点练1
(2022·湖北武汉二模)如图,圆台上底面圆O1半径为1,下底面圆O2半径为 ,AB为圆台下底面的一条直径,圆O2上点C满足AC=BC,PO1是圆台上底面的一条半径,点P,C在平面ABO1的同侧,且PO1∥BC.
(1)证明:平面PAC⊥平面ABC;
(2)若圆台的高为2,求直线AO1与平面PBC所成角的正弦值.
(1)证明 取AC的中点M,
所以四边形PO1O2M为平行四边形,则PM∥O1O2.
又O1O2⊥平面ABC,故PM⊥平面ABC.
又PM 平面PAC,故平面PAC⊥平面ABC.
考向2二面角
典例突破2
(12分)(2021·新高考Ⅱ·19)在四棱锥Q-ABCD中,底面ABCD是正方形,若AD=2,QD=QA= ,QC=3.
(1)证明:平面QAD⊥平面ABCD;
(2)求二面角B-QD-A的平面角的余弦值.
【规范解答】
(2)解:在平面ABCD内,过点O作OT∥CD,交BC于点T,则OT⊥AD,
结合(1)中的QO⊥平面ABCD,
故可建立如图所示的空间直角坐标系,
则D(0,1,0),Q(0,0,2),B(2,-1,0),
【教师讲评】
1.在(1)中,要证明面面垂直,需证明其中一个平面内的一条直线与另一个平面垂直.由条件中的数据可知△QAD为等腰三角形,从结论入手,反向思维,可知在△QAD中构造与AD垂直的线即与另一个平面垂直.
2.求二面角一般利用向量法,关键是建系,准确写出相关点的坐标,并寻找或计算两个平面的法向量,再根据公式计算即可.本题建系时可结合第(1)问的线面垂直及底面为正方形来构建.
增分技巧
利用空间向量求二面角的步骤
(1)分别求出两个半平面的一个法向量;
(2)求出两个法向量的夹角;
(3)根据图形判断二面角的平面角是锐角还是钝角,利用二面角的平面角与两个法向量的夹角的关系,求出二面角.
对点练2(2022·新高考Ⅱ·20)如图,PO是三棱锥P-ABC的高,PA=PB,AB⊥AC,E为PB的中点.
(1)证明:OE∥平面PAC;
(2)若∠ABO=∠CBO=30°,PO=3,PA=5,求二面角C-AE-B的正弦值.
(1)证明 连接OA,OB,如图所示.
∵PO是三棱锥P-ABC的高,∴PO⊥平面ABC,
∴PO⊥OA,PO⊥OB,∠POA=∠POB=90°.
又PA=PB,PO=PO,∴△POA≌△POB,∴OA=OB.
取AB的中点D,连接OD,DE,则OD⊥AB.
∵AB⊥AC,∴OD∥AC.
又AC 平面PAC,OD 平面PAC,∴OD∥平面PAC.
∵D,E分别是AB,PB的中点,∴DE∥PA.
又DE 平面PAC,PA 平面PAC,∴DE∥平面PAC.
∵OD∩DE=D,∴平面ODE∥平面PAC.
∵OE 平面ODE,∴OE∥平面PAC.
(2)解 过点D作DF∥OP,分别以DB,DO,DF所在直线为x轴、y轴、z轴,建立如下图所示的空间直角坐标系.
∵PO=3,PA=5,∴OA=4.
由(1)知OB=OA=4,又∠ABO=∠CBO=30°,
热点二 利用空间向量求距离
典例突破3
(2022·北京东城一模)如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,AB=AC=AA1=1,M为线段A1C1上一点.
(1)求证:BM⊥AB1;
(2)若直线AB1与平面BCM所成角为 ,求点A1到平面BCM的距离.
(1)证明 因为AA1⊥平面ABC,AB,AC 平面ABC,
所以AA1⊥AB,AA1⊥AC,而AB⊥AC,因此建立如图所示的空间直角坐标系,
则A(0,0,0),A1(0,0,1),B(1,0,0),C(0,1,0),B1(1,0,1).设M(0,a,1)(a∈[0,1]),
增分技巧
求点到平面的距离的四步骤
对点练3(2022·山东潍坊二模)如图,线段AC是圆O的直径,点B是圆O上异于A,C的点,AC=2,BC=1,PA⊥底面ABC,M是PB上的动点,且 (0<λ<1),N是线段PC的中点.
解 (1)直线l∥平面PBC,证明如下:
当λ= 时,M是线段PB的中点.因为N是线段PC的中点,所以MN∥BC.又BC 平面ABC,且MN 平面ABC,所以MN∥平面ABC.因为MN 平面AMN,且平面AMN∩平面ABC=l,所以MN∥l.又l 平面PBC,MN 平面PBC,所以直线l∥平面PBC.
(2)因为AC是圆O的直径,所以∠ABC=90°.
又AC=2,BC=1,所以AB= .
因为PA⊥平面ABC,BC 平面ABC,所以PA⊥BC.
又AB⊥BC,AB,BC 平面PBA,AB∩PA=A,
所以BC⊥平面PBA,而PB 平面PBA,故PB⊥BC,
以点B为坐标原点,BA,BC所在直线分别为x轴、y轴建立如图所示的空间直角坐标系,
热点三 空间中的探索性问题
考向1位置关系中的探索性问题
典例突破4
(2022·广东江门模拟)如图,在正四棱锥S-ABCD中,AC∩BD=O,SA= AB,P在侧棱SD上,SD⊥平面PAC.
(1)求平面SAB与平面PAC所成的二面角的余弦值;
(2)侧棱SC上是否存在一点E,使得BE∥平面PAC
若存在,求SE∶EC的值;若不存在,请说明理由.
解 (1)如图,由题意知SO⊥平面ABCD,AC⊥BD,故OS,OB,OC两两垂直.
增分技巧
立体几何中探索性问题的求解策略
(1)探索性问题的一般解法:
①可先猜后证,即先观察并尝试给出条件再证明.
②首先假设结论成立,然后把这个假设作为已知条件,与题目的其他已知条件一起进行推理论证和计算.在推理论证和计算无误的前提下,若得到一个合理的结论,则说明假设成立;若得到一个不合理的结论,则说明假设不成立.
(2)涉及在线段上是否存在符合某条件的点的问题,可以先根据条件猜测点的位置,特别注意特殊位置关系和极端情形的应用.
(3)可借助空间直角坐标系将动点用坐标(含参数)表示出来,然后根据已知条件建立关于参数的方程(组),由此解决探索性问题.
对点练4
(2022·江苏苏锡常镇二模)如图,在四棱锥S-ABCD中,已知四边形ABCD为菱形,∠BAD=60°,△SAD为正三角形,平面SAD⊥平面ABCD.
(1)求二面角S-BC-A的大小;
(2)在线段SC上是否存在一点M(端点S,C除外),使得AM⊥BD 若存在,指出点M的位置;若不存在,请说明理由.
解 (1)取AD中点O,连接SO,BO.因为SA=SD,OA=OD,所以SO⊥AD,即SO⊥OA.又因为平面SAD⊥平面ABCD,平面SAD∩平面ABCD=AD,SO 平面SAD,则SO⊥平面ABCD.因为OB 平面ABCD,所以SO⊥OB.
因为BA=BD,OA=OD,所以AO⊥OB,
所以OA,OB,OS两两垂直.
以O为坐标原点建立如图所示空间直角坐标系,设AD=2,则
考向2与空间角有关的探索性问题
典例突破5
(2022·山东德州二模)在《九章算术·商功》中提到的“阳马”这一几何体,是指底面为矩形,有一条侧棱垂直于底面的四棱锥,现有“阳马”P-ABCD,底面为边长为2的正方形,侧棱PA⊥平面ABCD,PA=2,E,F为边BC,CD上的点,
(2)是否存在实数λ(0<λ<1),使二面角P-EF-A的大小为45° 如果不存在,请说明理由;如果存在,求此时直线BM与平面PEF所成角的正弦值.
(1)证明 当λ= 时,点E,F为线段BC,CD的中点.连接AF与BM交于点G,
在△ABM和△DAF中,AB=AD,AM=DF,∠BAM=∠ADF=90°,所以△ABM≌△DAF,故∠ABM=∠FAD.而∠FAD+∠BAF=90°,所以∠ABM+∠BAF=90°,故∠AGB=90°,即BM⊥AF.又PA⊥平面ABCD,BM 平面ABCD,所以PA⊥BM.又PA,AF 平面PAF,PA∩AF=A,所以BM⊥平面PAF.又因为BM 平面PBM,所以平面PBM⊥平面PAF.
(2)解 存在.连接AC交EF于点Q,连接PQ,BD与AC交于点O,如图所示.
所以AC⊥EF.
因为PA⊥平面ABCD,EF 平面ABCD,则PA⊥EF,
而PA,AC 平面PAC,PA∩AC=A,故EF⊥平面PAC.
因为PQ 平面PAC,则PQ⊥EF,
所以∠AQP为二面角P-EF-A的一个平面角.
增分技巧
与空间向量有关的探索性问题主要有两类:一类是探究线面的位置关系;另一类是探究线面角或二面角满足特定要求时的存在性问题.处理原则是:先建立空间直角坐标系,引入参数(有些是题中已给出),设出关键点的坐标,然后探究这样的点是否存在,或参数是否满足要求,从而作出判断.
对点练5
(2022·湖南师大附中二模)在三棱柱ABC-A1B1C1中,四边形AA1B1B是菱形,AB⊥AC,平面AA1B1B⊥平面ABC,平面A1B1C1与平面AB1C的交线为l.
(1)证明:A1B⊥B1C;
(2)若∠ABB1=60°,AB=AC=2,直线l上是否存在点P,
使得A1B与平面ABP所成角为60° 若存在,求B1P的
长度;若不存在,请说明理由.
(1)证明 因为四边形AA1B1B为菱形,所以A1B⊥AB1.因为平面AA1B1B⊥平面ABC,平面AA1B1B∩平面ABC=AB,AC 平面ABC,AC⊥AB,所以AC⊥平面AA1B1B.
又A1B 平面AA1B1B,所以AC⊥A1B.
又AB1,AC 平面B1AC,AB1∩AC=A,所以A1B⊥平面B1AC.又B1C 平面B1AC,所以A1B⊥B1C.
(2)解 直线l上不存在点P,使A1B与平面ABP所成角为60°.理由如下:
取线段A1B1中点D,连接AD.
因为∠ABB1=60°,所以∠AA1B1=60°.又AA1=A1B1,所以△AA1B1为等边三角形,所以AD⊥A1B1.
因为A1B1∥AB,所以AD⊥AB.
因为平面AA1B1B⊥平面ABC,平面AA1B1B∩平面ABC=AB,AD 平面AA1B1B,所以AD⊥平面ABC.
因为AC∥A1C1,AC 平面A1B1C1,A1C1 平面A1B1C1,所以AC∥平面A1B1C1.又因为AC 平面AB1C,平面A1B1C1∩平面AB1C=l,所以AC∥l.
假设l上存在一点P,使A1B与平面ABP所成角为60°.
同课章节目录
