2023届高中数学二轮复习第1讲新高考新题型 课件(30张)
文档属性
| 名称 | 2023届高中数学二轮复习第1讲新高考新题型 课件(30张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 14:30:08 | ||
图片预览










文档简介
(共30张PPT)
第1讲 新高考新题型
序篇
2023
《中国高考评价体系》指出:要命制结论开放、解题方法多样、答案不唯一的试题,增强试题的开放性和探究性,引导学生打破常规,进行独立思考和判断,提出解决问题的方案.高考试题逐渐增加基础性、综合性、应用性、探究性和开放性,落实立德树人的根本任务,推动人才培养的改革创新.从近几年高考试题来看,多选题成为新高考必考题型,双空题、开放题、结构不良题等新题型也时常出现.
新题型一多选题
多选题常常同时对多个知识点进行考查,也可对同一对象从不同角度进行考查,具有一定的综合性.解法多样,可以用直接法、验证法、反例法、排除法、数形结合法等,需对每个选项作出正确判断.但如果能排除两个错误选项,则可知剩余两个必然正确.
例1(1)(2022·新高考Ⅰ·9)已知正方体ABCD-A1B1C1D1,则( )
A.直线BC1与DA1所成的角为90°
B.直线BC1与CA1所成的角为90°
C.直线BC1与平面BB1D1D所成的角为45°
D.直线BC1与平面ABCD所成的角为45°
答案 (1)ABD (2)AD
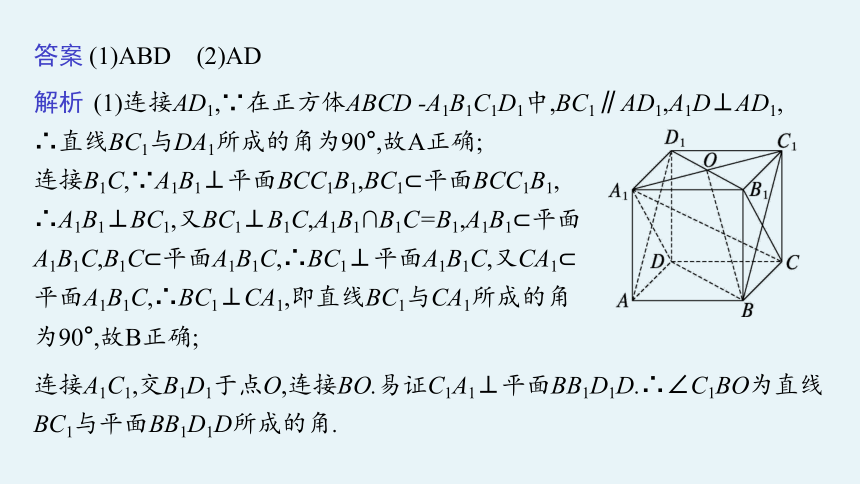
解析 (1)连接AD1,∵在正方体ABCD -A1B1C1D1中,BC1∥AD1,A1D⊥AD1,
∴直线BC1与DA1所成的角为90°,故A正确;
连接B1C,∵A1B1⊥平面BCC1B1,BC1 平面BCC1B1,
∴A1B1⊥BC1,又BC1⊥B1C,A1B1∩B1C=B1,A1B1 平面
A1B1C,B1C 平面A1B1C,∴BC1⊥平面A1B1C,又CA1
平面A1B1C,∴BC1⊥CA1,即直线BC1与CA1所成的角
为90°,故B正确;
连接A1C1,交B1D1于点O,连接BO.易证C1A1⊥平面BB1D1D.∴∠C1BO为直线BC1与平面BB1D1D所成的角.
∵C1C⊥平面ABCD,∴∠C1BC为直线BC1与平面ABCD所成的角.又∠C1BC=45°,∴直线BC1与平面ABCD所成的角为45°,故D正确.故选ABD.
新题型二双空题
双空题一般分为两类:
(1)递进式:两空之间有联系,第一空的结果是第二空的条件,第一空一般比较简单,但它的正确求解是第二空解答的关键.
(2)分列式:两个空的设问相当于一个题目背景下的两道填空题,两问之间没有具体联系,各自成题,是对多个知识点或某知识点的多角度考查.第一空不会,也不影响第二空的解答.
(2)(2021·新高考Ⅰ·16)某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把纸对折.规格为20 dm×12 dm的长方形纸,对折1次共可以得到10 dm×12 dm,20 dm×6 dm两种规格的图形,它们的面积之和S1=240 dm2,对折2次共可以得到5 dm×12 dm,10 dm×6 dm,20 dm×3 dm 三种规格的图形,它们的面积之和S2=180 dm2,以此类推.则对折4次共可以得到不同规格图形的种数为 ;如果对折n次,那么
新题型三开放型填空题
开放型填空题的特点是正确的答案不唯一,一般可分为:
(1)探索型,如条件的探索、结论的探索等;
(2)信息迁移型;
(3)组合型等.
例3(1)(2022·全国甲·文15)记双曲线C: =1(a>0,b>0)的离心率为e,写出满足条件“直线y=2x与C无公共点”的e的一个值 .
(2)(2021·北京·14)若点A(cos θ,sin θ)关于y轴的对称点为B(cos(θ+ ),sin(θ+ )),则θ的一个取值为 .
新题型四结构不良型解答题
结构不良型解答题多在解三角形、数列、立体几何等部分命制,有时也可能以解析几何为背景.一般有两种类型:一是三选一或二选一作为题目条件进行求解;二是给出的几个选择条件中只能由其中两个推出另一个正确,要求做出判断并证明.
因此,选条件①时,问题中的三角形存在,此时c=1.
例5(2022·北京·17)如图,在三棱柱ABC-A1B1C1中,侧面BCC1B1为正方形,平面BCC1B1⊥平面ABB1A1,AB=BC=2,M,N分别为A1B1,AC的中点.
(1)求证:MN∥平面BCC1B1;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.
条件①:AB⊥MN;
条件②:BM=MN.
(1)证明 取BC的中点D,连接B1D,DN.在三棱柱ABC-A1B1C1中,A1B1∥AB,A1B1=AB.
因为点M,N,D分别为A1B1,AC,BC的中点,
所以四边形B1MND为平行四边形,因此B1D∥MN.
又MN 平面BCC1B1,B1D 平面BCC1B1,
所以MN∥平面BCC1B1.
(2)解 选条件①:
因为侧面BCC1B1为正方形,所以CB⊥BB1.
因为平面BCC1B1⊥平面ABB1A1,且平面BCC1B1∩平面ABB1A1=BB1,所以CB⊥平面ABB1A1.
又AB 平面ABB1A1,所以CB⊥AB.
由(1)得B1D∥MN,因为AB⊥MN,所以AB⊥B1D.
而B1D∩CB=D,所以AB⊥平面BCC1B1.
又BB1 平面BCC1B1,所以AB⊥BB1.
在三棱柱ABC-A1B1C1中,BA,BC,BB1两两垂直,故以B为坐标原点,分别以BC,BA,BB1为x轴、y轴、z轴,建立如图所示的空间直角坐标系,因为AB=BC=BB1=2,所以B(0,0,0),N(1,1,0),M(0,1,2),A(0,2,0),
选条件②:
取AB的中点H,连接HM,HN.
因为点M,N,H分别为A1B1,AC,AB的中点,
所以B1B∥MH,CB∥NH,而CB⊥BB1,
故NH⊥MH,即∠MHN=90°.
又因为AB=BC=2,所以NH=BH=1.
在△MNH和△MBH中,因为MH=MH,NH=BH,BM=MN,所以△MNH≌△MBH.
又∠MHN=90°,所以∠MHB=∠MHN=90°,即MH⊥BH.又MH∥BB1,所以BB1⊥BA.
因为平面BCC1B1⊥平面ABB1A1,且平面BCC1B1∩平面ABB1A1=BB1,又CB⊥BB1,所以CB⊥平面ABB1A1.
又AB 平面ABB1A1,所以CB⊥AB.
所以在三棱柱ABC-A1B1C1中,BA,BC,BB1两两垂直,故以点B为坐标原点,分别以BC,BA,BB1为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
因为AB=BC=BB1=2,所以B(0,0,0),N(1,1,0),M(0,1,2),A(0,2,0),所以
设平面BMN的法向量为n=(x,y,z),
第1讲 新高考新题型
序篇
2023
《中国高考评价体系》指出:要命制结论开放、解题方法多样、答案不唯一的试题,增强试题的开放性和探究性,引导学生打破常规,进行独立思考和判断,提出解决问题的方案.高考试题逐渐增加基础性、综合性、应用性、探究性和开放性,落实立德树人的根本任务,推动人才培养的改革创新.从近几年高考试题来看,多选题成为新高考必考题型,双空题、开放题、结构不良题等新题型也时常出现.
新题型一多选题
多选题常常同时对多个知识点进行考查,也可对同一对象从不同角度进行考查,具有一定的综合性.解法多样,可以用直接法、验证法、反例法、排除法、数形结合法等,需对每个选项作出正确判断.但如果能排除两个错误选项,则可知剩余两个必然正确.
例1(1)(2022·新高考Ⅰ·9)已知正方体ABCD-A1B1C1D1,则( )
A.直线BC1与DA1所成的角为90°
B.直线BC1与CA1所成的角为90°
C.直线BC1与平面BB1D1D所成的角为45°
D.直线BC1与平面ABCD所成的角为45°
答案 (1)ABD (2)AD
解析 (1)连接AD1,∵在正方体ABCD -A1B1C1D1中,BC1∥AD1,A1D⊥AD1,
∴直线BC1与DA1所成的角为90°,故A正确;
连接B1C,∵A1B1⊥平面BCC1B1,BC1 平面BCC1B1,
∴A1B1⊥BC1,又BC1⊥B1C,A1B1∩B1C=B1,A1B1 平面
A1B1C,B1C 平面A1B1C,∴BC1⊥平面A1B1C,又CA1
平面A1B1C,∴BC1⊥CA1,即直线BC1与CA1所成的角
为90°,故B正确;
连接A1C1,交B1D1于点O,连接BO.易证C1A1⊥平面BB1D1D.∴∠C1BO为直线BC1与平面BB1D1D所成的角.
∵C1C⊥平面ABCD,∴∠C1BC为直线BC1与平面ABCD所成的角.又∠C1BC=45°,∴直线BC1与平面ABCD所成的角为45°,故D正确.故选ABD.
新题型二双空题
双空题一般分为两类:
(1)递进式:两空之间有联系,第一空的结果是第二空的条件,第一空一般比较简单,但它的正确求解是第二空解答的关键.
(2)分列式:两个空的设问相当于一个题目背景下的两道填空题,两问之间没有具体联系,各自成题,是对多个知识点或某知识点的多角度考查.第一空不会,也不影响第二空的解答.
(2)(2021·新高考Ⅰ·16)某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把纸对折.规格为20 dm×12 dm的长方形纸,对折1次共可以得到10 dm×12 dm,20 dm×6 dm两种规格的图形,它们的面积之和S1=240 dm2,对折2次共可以得到5 dm×12 dm,10 dm×6 dm,20 dm×3 dm 三种规格的图形,它们的面积之和S2=180 dm2,以此类推.则对折4次共可以得到不同规格图形的种数为 ;如果对折n次,那么
新题型三开放型填空题
开放型填空题的特点是正确的答案不唯一,一般可分为:
(1)探索型,如条件的探索、结论的探索等;
(2)信息迁移型;
(3)组合型等.
例3(1)(2022·全国甲·文15)记双曲线C: =1(a>0,b>0)的离心率为e,写出满足条件“直线y=2x与C无公共点”的e的一个值 .
(2)(2021·北京·14)若点A(cos θ,sin θ)关于y轴的对称点为B(cos(θ+ ),sin(θ+ )),则θ的一个取值为 .
新题型四结构不良型解答题
结构不良型解答题多在解三角形、数列、立体几何等部分命制,有时也可能以解析几何为背景.一般有两种类型:一是三选一或二选一作为题目条件进行求解;二是给出的几个选择条件中只能由其中两个推出另一个正确,要求做出判断并证明.
因此,选条件①时,问题中的三角形存在,此时c=1.
例5(2022·北京·17)如图,在三棱柱ABC-A1B1C1中,侧面BCC1B1为正方形,平面BCC1B1⊥平面ABB1A1,AB=BC=2,M,N分别为A1B1,AC的中点.
(1)求证:MN∥平面BCC1B1;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.
条件①:AB⊥MN;
条件②:BM=MN.
(1)证明 取BC的中点D,连接B1D,DN.在三棱柱ABC-A1B1C1中,A1B1∥AB,A1B1=AB.
因为点M,N,D分别为A1B1,AC,BC的中点,
所以四边形B1MND为平行四边形,因此B1D∥MN.
又MN 平面BCC1B1,B1D 平面BCC1B1,
所以MN∥平面BCC1B1.
(2)解 选条件①:
因为侧面BCC1B1为正方形,所以CB⊥BB1.
因为平面BCC1B1⊥平面ABB1A1,且平面BCC1B1∩平面ABB1A1=BB1,所以CB⊥平面ABB1A1.
又AB 平面ABB1A1,所以CB⊥AB.
由(1)得B1D∥MN,因为AB⊥MN,所以AB⊥B1D.
而B1D∩CB=D,所以AB⊥平面BCC1B1.
又BB1 平面BCC1B1,所以AB⊥BB1.
在三棱柱ABC-A1B1C1中,BA,BC,BB1两两垂直,故以B为坐标原点,分别以BC,BA,BB1为x轴、y轴、z轴,建立如图所示的空间直角坐标系,因为AB=BC=BB1=2,所以B(0,0,0),N(1,1,0),M(0,1,2),A(0,2,0),
选条件②:
取AB的中点H,连接HM,HN.
因为点M,N,H分别为A1B1,AC,AB的中点,
所以B1B∥MH,CB∥NH,而CB⊥BB1,
故NH⊥MH,即∠MHN=90°.
又因为AB=BC=2,所以NH=BH=1.
在△MNH和△MBH中,因为MH=MH,NH=BH,BM=MN,所以△MNH≌△MBH.
又∠MHN=90°,所以∠MHB=∠MHN=90°,即MH⊥BH.又MH∥BB1,所以BB1⊥BA.
因为平面BCC1B1⊥平面ABB1A1,且平面BCC1B1∩平面ABB1A1=BB1,又CB⊥BB1,所以CB⊥平面ABB1A1.
又AB 平面ABB1A1,所以CB⊥AB.
所以在三棱柱ABC-A1B1C1中,BA,BC,BB1两两垂直,故以点B为坐标原点,分别以BC,BA,BB1为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
因为AB=BC=BB1=2,所以B(0,0,0),N(1,1,0),M(0,1,2),A(0,2,0),所以
设平面BMN的法向量为n=(x,y,z),
同课章节目录
