2023届高中数学二轮复习第2讲新情境新命题 课件(25张)
文档属性
| 名称 | 2023届高中数学二轮复习第2讲新情境新命题 课件(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 14:30:35 | ||
图片预览




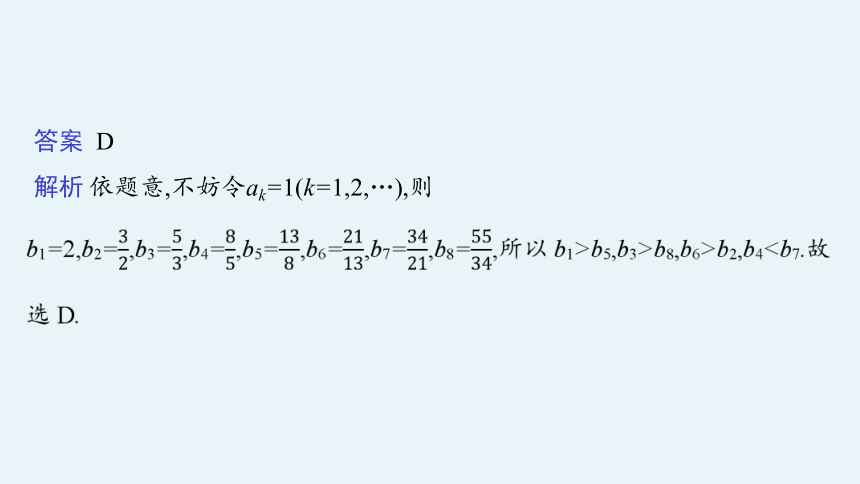


文档简介
(共25张PPT)
第2讲 新情境新命题
序篇
2023
新高考试题突出对情境应用题的考查,引导学生由“解题”向“解决问题”方向转变.试题情境贴近时代、贴近社会、贴近生活,以前沿科技、社会热点、传统文化、日常生活中的实际问题为背景,考查考生运用数学知识解决实际问题的能力,强调以数学核心素养为导向,常以图、表、文并用的方式呈现,情境新颖,信息量大,解题的关键是数学建模.
一、关注科技前沿,树立远大志向
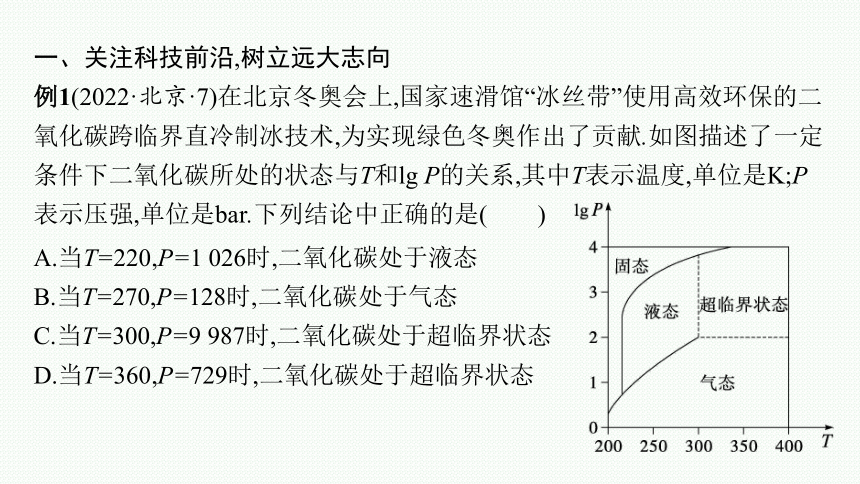
例1(2022·北京·7)在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献.如图描述了一定条件下二氧化碳所处的状态与T和lg P的关系,其中T表示温度,单位是K;P表示压强,单位是bar.下列结论中正确的是( )
A.当T=220,P=1 026时,二氧化碳处于液态
B.当T=270,P=128时,二氧化碳处于气态
C.当T=300,P=9 987时,二氧化碳处于超临界状态
D.当T=360,P=729时,二氧化碳处于超临界状态
答案 D
解析 对于选项A,lg P=lg 1 026>3,T=220,根据图象可知二氧化碳处于固态;对于选项B,lg P=lg 128>2,T=270,根据图象可知二氧化碳处于液态;对于选项C,lg P=lg 9 987≈3.999,T=300,根据图象可知二氧化碳处于固态;对于选项D,lg P=lg 729>2,T=360,根据图象可知二氧化碳处于超临界状态.故选D.
例2(2022·全国乙·理4)嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国第一颗环绕太阳飞行的人造行星.为研究嫦娥二号绕日周期与地
球绕日周期的比值,用到数列{bn}: ,…,
依此类推,其中ak∈N*(k=1,2,…).则( )
A.b1C.b6答案 D
解析 依题意,不妨令ak=1(k=1,2,…),则
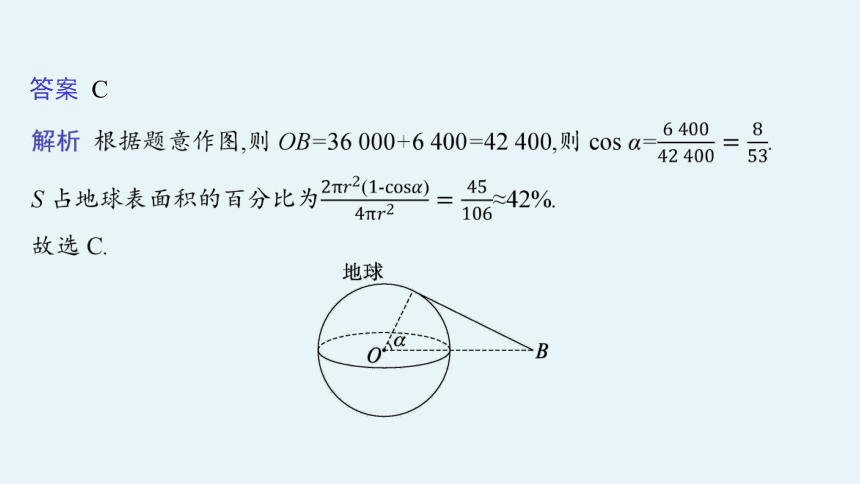
例3(2021·新高考Ⅱ·4)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为36 000 km(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O,半径r为6 400 km的球,其上点A的纬度是指OA与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α,记卫星信号覆盖地球表面的表面积为S=2πr2(1-cos α)(单位:km2),则S占地球表面积的百分比约为( )
A.26% B.34% C.42% D.50%
答案 C
二、聚焦社会热点,彰显责任担当
例4(2021·全国甲·理4)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录法的数据V满足L=5+lg V.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据约为( ≈1.259)( )
A.1.5 B.1.2 C.0.8 D.0.6
答案 C
解析 由题意L=5+lg V,当L=4.9时,有4.9=5+lg V,lg V=-0.1,
例5(2022·山东聊城三模)2021年4月12日,四川省三星堆遗址考古发掘3号坑出土一件完整的圆口方尊,这是经科学考古发掘出土的首件完整圆口方尊(图1),它的基座沉稳,象征“地载万物”,顶部舒展开翩,寓意迎接纯洁的奥林匹克火种,一种圆口方尊的上部(图2)外形近似为双曲线的一部分绕着虚
轴所在的直线旋转形成的曲面,该曲面的高为50 cm,上口直径为 cm,下口直径为25 cm,最小横截面的直径为20 cm,则该双曲线的离心率为( )
图1
图2
答案 D
三、弘扬传统文化,增强民族自信
例6(2022·新高考Ⅱ·3)中国的古建筑不仅是挡风遮雨的住处,更是美学和哲学的体现.如图1是某古建筑物中的举架结构,AA',BB',CC',DD'是桁,相邻桁的水平距离称为步,垂直距离称为举.图2是某古代建筑屋顶截面的示意图.其中DD1,CC1,BB1,AA1是脊,OD1,DC1,CB1,BA1是相等的步,相邻桁的举步的比分别为 ,若k1,k2,k3是公差为0.1的等差数列,直线OA的斜率为0.725,则k3=( )
A.0.75 B.0.8 C.0.85 D.0.9
图1
图2
答案 D
解析 不妨设OD1=DC1=CB1=BA1=1,则DD1=0.5,CC1=k1,BB1=k2,AA1=k3.
答案 B
例8(2020·全国Ⅱ·理4)北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层.上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块.下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块.已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)( )
A.3 699块 B.3 474块
C.3 402块 D.3 339块
答案 C
解析 由题意可知,从上到下,从内到外,每环的扇面形石板数构成以9为首项,9为公差的等差数列,设为{an}.
设上层有n环,则上层扇面形石板总数为Sn,中层扇面形石板总数为S2n-Sn,下层扇面形石板总数为S3n-S2n,三层扇面形石板总数为S3n.因为{an}为等差数列,所以Sn,S2n-Sn,S3n-S2n构成等差数列,公差为9n2.因为下层比中层多729块,
四、注重五育并举,培育时代新人
例9(2020·全国Ⅱ·文3)如图,将钢琴上的12个键依次记为a1,a2,…,a12.设1≤iA.5 B.8 C.10 D.15
答案 C
解析 结合题意,原位大三和弦有(a1,a5,a8),(a2,a6,a9),(a3,a7,a10),(a4,a8,a11),
(a5,a9,a12),共5个,原位小三和弦有(a1,a4,a8),(a2,a5,a9),(a3,a6,a10),(a4,a7,a11),
(a5,a8,a12),共5个,故原位大三和弦与原位小三和弦的个数之和为5+5=10.故选C.
例10(2020·山东·15)某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O为圆孔及轮廓圆弧AB所在圆的圆心,A是圆弧AB与直线AG的切点,B是圆弧AB与直线BC的切点,四边形DEFG为矩形,BC⊥DG,垂足为C,tan∠ODC= ,BH∥DG,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为 cm2.
解析 作OM⊥CG交CG于点M,AP⊥OH交OH于点P,AQ⊥CG交CG于点Q,图略.
设OM=3x,则DM=5x,∴OP=MQ=7-5x,
五、贴近现实生活,培养应用意识
例11(多选)(2020·海南·9)我国新冠肺炎疫情防控进入常态化,各地有序推动复工复产.下面是某地连续11天的复工、复产指数折线图.
根据该折线图,( )
A.这11天复工指数和复产指数均逐日增加
B.在这11天期间,复产指数的增量大于复工指数的增量
C.第3天至第11天,复工指数和复产指数都超过80%
D.第9天至第11天,复产指数的增量大于复工指数的增量
答案 CD
解析 由题图可知第8,9天复工指数和复产指数均减小,故A错误;第1天时复工指数小于复产指数,第11天时两指数相等,故复产指数的增量小于复工指数的增量,故B错误;由题图可知第3天至第11天,复工指数和复产指数都超过80%,故C正确;第9天至第11天,复产指数的增量大于复工指数的增量,故D正确.
第2讲 新情境新命题
序篇
2023
新高考试题突出对情境应用题的考查,引导学生由“解题”向“解决问题”方向转变.试题情境贴近时代、贴近社会、贴近生活,以前沿科技、社会热点、传统文化、日常生活中的实际问题为背景,考查考生运用数学知识解决实际问题的能力,强调以数学核心素养为导向,常以图、表、文并用的方式呈现,情境新颖,信息量大,解题的关键是数学建模.
一、关注科技前沿,树立远大志向
例1(2022·北京·7)在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献.如图描述了一定条件下二氧化碳所处的状态与T和lg P的关系,其中T表示温度,单位是K;P表示压强,单位是bar.下列结论中正确的是( )
A.当T=220,P=1 026时,二氧化碳处于液态
B.当T=270,P=128时,二氧化碳处于气态
C.当T=300,P=9 987时,二氧化碳处于超临界状态
D.当T=360,P=729时,二氧化碳处于超临界状态
答案 D
解析 对于选项A,lg P=lg 1 026>3,T=220,根据图象可知二氧化碳处于固态;对于选项B,lg P=lg 128>2,T=270,根据图象可知二氧化碳处于液态;对于选项C,lg P=lg 9 987≈3.999,T=300,根据图象可知二氧化碳处于固态;对于选项D,lg P=lg 729>2,T=360,根据图象可知二氧化碳处于超临界状态.故选D.
例2(2022·全国乙·理4)嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国第一颗环绕太阳飞行的人造行星.为研究嫦娥二号绕日周期与地
球绕日周期的比值,用到数列{bn}: ,…,
依此类推,其中ak∈N*(k=1,2,…).则( )
A.b1
解析 依题意,不妨令ak=1(k=1,2,…),则
例3(2021·新高考Ⅱ·4)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为36 000 km(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O,半径r为6 400 km的球,其上点A的纬度是指OA与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α,记卫星信号覆盖地球表面的表面积为S=2πr2(1-cos α)(单位:km2),则S占地球表面积的百分比约为( )
A.26% B.34% C.42% D.50%
答案 C
二、聚焦社会热点,彰显责任担当
例4(2021·全国甲·理4)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录法的数据V满足L=5+lg V.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据约为( ≈1.259)( )
A.1.5 B.1.2 C.0.8 D.0.6
答案 C
解析 由题意L=5+lg V,当L=4.9时,有4.9=5+lg V,lg V=-0.1,
例5(2022·山东聊城三模)2021年4月12日,四川省三星堆遗址考古发掘3号坑出土一件完整的圆口方尊,这是经科学考古发掘出土的首件完整圆口方尊(图1),它的基座沉稳,象征“地载万物”,顶部舒展开翩,寓意迎接纯洁的奥林匹克火种,一种圆口方尊的上部(图2)外形近似为双曲线的一部分绕着虚
轴所在的直线旋转形成的曲面,该曲面的高为50 cm,上口直径为 cm,下口直径为25 cm,最小横截面的直径为20 cm,则该双曲线的离心率为( )
图1
图2
答案 D
三、弘扬传统文化,增强民族自信
例6(2022·新高考Ⅱ·3)中国的古建筑不仅是挡风遮雨的住处,更是美学和哲学的体现.如图1是某古建筑物中的举架结构,AA',BB',CC',DD'是桁,相邻桁的水平距离称为步,垂直距离称为举.图2是某古代建筑屋顶截面的示意图.其中DD1,CC1,BB1,AA1是脊,OD1,DC1,CB1,BA1是相等的步,相邻桁的举步的比分别为 ,若k1,k2,k3是公差为0.1的等差数列,直线OA的斜率为0.725,则k3=( )
A.0.75 B.0.8 C.0.85 D.0.9
图1
图2
答案 D
解析 不妨设OD1=DC1=CB1=BA1=1,则DD1=0.5,CC1=k1,BB1=k2,AA1=k3.
答案 B
例8(2020·全国Ⅱ·理4)北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层.上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块.下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块.已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)( )
A.3 699块 B.3 474块
C.3 402块 D.3 339块
答案 C
解析 由题意可知,从上到下,从内到外,每环的扇面形石板数构成以9为首项,9为公差的等差数列,设为{an}.
设上层有n环,则上层扇面形石板总数为Sn,中层扇面形石板总数为S2n-Sn,下层扇面形石板总数为S3n-S2n,三层扇面形石板总数为S3n.因为{an}为等差数列,所以Sn,S2n-Sn,S3n-S2n构成等差数列,公差为9n2.因为下层比中层多729块,
四、注重五育并举,培育时代新人
例9(2020·全国Ⅱ·文3)如图,将钢琴上的12个键依次记为a1,a2,…,a12.设1≤i
答案 C
解析 结合题意,原位大三和弦有(a1,a5,a8),(a2,a6,a9),(a3,a7,a10),(a4,a8,a11),
(a5,a9,a12),共5个,原位小三和弦有(a1,a4,a8),(a2,a5,a9),(a3,a6,a10),(a4,a7,a11),
(a5,a8,a12),共5个,故原位大三和弦与原位小三和弦的个数之和为5+5=10.故选C.
例10(2020·山东·15)某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O为圆孔及轮廓圆弧AB所在圆的圆心,A是圆弧AB与直线AG的切点,B是圆弧AB与直线BC的切点,四边形DEFG为矩形,BC⊥DG,垂足为C,tan∠ODC= ,BH∥DG,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为 cm2.
解析 作OM⊥CG交CG于点M,AP⊥OH交OH于点P,AQ⊥CG交CG于点Q,图略.
设OM=3x,则DM=5x,∴OP=MQ=7-5x,
五、贴近现实生活,培养应用意识
例11(多选)(2020·海南·9)我国新冠肺炎疫情防控进入常态化,各地有序推动复工复产.下面是某地连续11天的复工、复产指数折线图.
根据该折线图,( )
A.这11天复工指数和复产指数均逐日增加
B.在这11天期间,复产指数的增量大于复工指数的增量
C.第3天至第11天,复工指数和复产指数都超过80%
D.第9天至第11天,复产指数的增量大于复工指数的增量
答案 CD
解析 由题图可知第8,9天复工指数和复产指数均减小,故A错误;第1天时复工指数小于复产指数,第11天时两指数相等,故复产指数的增量小于复工指数的增量,故B错误;由题图可知第3天至第11天,复工指数和复产指数都超过80%,故C正确;第9天至第11天,复产指数的增量大于复工指数的增量,故D正确.
同课章节目录
