2023届高考数学二轮复习第二讲结构不良问题的命题特点与解题策略课件(20张)
文档属性
| 名称 | 2023届高考数学二轮复习第二讲结构不良问题的命题特点与解题策略课件(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 498.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 20:37:03 | ||
图片预览



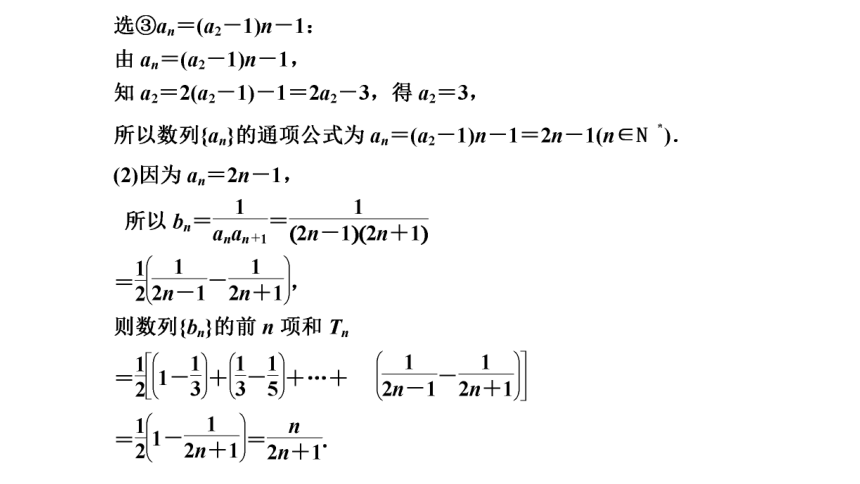





文档简介
(共20张PPT)
第二讲 结构不良问题的命题特点与解题策略
结构不良问题具有条件模糊、解决方案多样、结果开放等特点,其解决过程能有效激发学生求知欲、帮助学生多角度把握问题本质、追寻知识背后的价值.因此,解决结构不良问题对考查学生的素养和能力,发挥考试的选拔功能、促进学生素养的养成和能力的提升具有深远意义.
结构不良问题一般具有初始状态、目标状态、中间状态至少有一个不确定的特点,常见的主要类型有:
(1)问题目标明确、条件多种选择;(2)问题目标界定不明确;(3)问题解决具有多种方法、途径;(4)问题条件或数据冗余.
[微点评]
通过这样的设计,目的是希望学生在具体解答题目前有初步的判断,在各种选择当中选一个自己擅长的或自认为有把握的,给学生搭建展示自己的平台.
[思路点拨] 本题(2)问基于直线AB过同一个定点,但定点究竟是哪个点尚不明确,需要从李同学的条件入手,得到直线过定点(0,4),再结合刘同学的条件,求得实数a的值.
问题解决具有多种方法、途径
[例3] 在①OH∥平面PAB,②平面PAB⊥平面OHC,③OH⊥PC这三个条件中任选一个,补充在下面的问题中,并解决该问题.
问题:如图,在三棱锥P?ABC中,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,AC=16,PA=PC=10,O为AC中点,H为△PBC内的动点(含边界).
(1)求点O到平面PBC的距离;
(2)若________,求直线PH与平面ABC所成角的正弦值的取值范围.
删②.
在△ABD中,由余弦定理有
BD2=AB2+AD2-2AB·AD·cos A,
即7=9+AD2-6AD·cos 60°,解得AD=1或AD=2,
则AC=2或4,有2解,不满足题意.
删③.
在△ABC中,由余弦定理可得BC2=AB2+AC2-2AB·AC·cos A,
即7=9+AC2-6AC·cos 60°,解得AC=1或2,有2解,不满足题意.
在教学中,结构不良问题的设计要以主题式、项目式组织情境和问题,为讨论式学习、合作探究式学习提供多维度思考空间,更好地拓展学生思维广度,更好地促进学生交流合作,从而激发学生的思维创新能力,提高学生的合作能力.运用其结构不良特性,更好地激发学生学习兴趣,更好地培养学生发现问题、解决问题的能力,以及应对现实挑战的创新能力和实践能力.因此,结构不良问题设计要根据其特性,一方面对真实的情境进行适当地加工,使其蕴含着有价值的问题,期待学生从多个视角去发现、探究它;另一方面对条件、结论、方法等问题结构要素进行合理设置,或使条件部分呈现,或调用的概念、原理不明确,或解决方法多样.
第二讲 结构不良问题的命题特点与解题策略
结构不良问题具有条件模糊、解决方案多样、结果开放等特点,其解决过程能有效激发学生求知欲、帮助学生多角度把握问题本质、追寻知识背后的价值.因此,解决结构不良问题对考查学生的素养和能力,发挥考试的选拔功能、促进学生素养的养成和能力的提升具有深远意义.
结构不良问题一般具有初始状态、目标状态、中间状态至少有一个不确定的特点,常见的主要类型有:
(1)问题目标明确、条件多种选择;(2)问题目标界定不明确;(3)问题解决具有多种方法、途径;(4)问题条件或数据冗余.
[微点评]
通过这样的设计,目的是希望学生在具体解答题目前有初步的判断,在各种选择当中选一个自己擅长的或自认为有把握的,给学生搭建展示自己的平台.
[思路点拨] 本题(2)问基于直线AB过同一个定点,但定点究竟是哪个点尚不明确,需要从李同学的条件入手,得到直线过定点(0,4),再结合刘同学的条件,求得实数a的值.
问题解决具有多种方法、途径
[例3] 在①OH∥平面PAB,②平面PAB⊥平面OHC,③OH⊥PC这三个条件中任选一个,补充在下面的问题中,并解决该问题.
问题:如图,在三棱锥P?ABC中,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,AC=16,PA=PC=10,O为AC中点,H为△PBC内的动点(含边界).
(1)求点O到平面PBC的距离;
(2)若________,求直线PH与平面ABC所成角的正弦值的取值范围.
删②.
在△ABD中,由余弦定理有
BD2=AB2+AD2-2AB·AD·cos A,
即7=9+AD2-6AD·cos 60°,解得AD=1或AD=2,
则AC=2或4,有2解,不满足题意.
删③.
在△ABC中,由余弦定理可得BC2=AB2+AC2-2AB·AC·cos A,
即7=9+AC2-6AC·cos 60°,解得AC=1或2,有2解,不满足题意.
在教学中,结构不良问题的设计要以主题式、项目式组织情境和问题,为讨论式学习、合作探究式学习提供多维度思考空间,更好地拓展学生思维广度,更好地促进学生交流合作,从而激发学生的思维创新能力,提高学生的合作能力.运用其结构不良特性,更好地激发学生学习兴趣,更好地培养学生发现问题、解决问题的能力,以及应对现实挑战的创新能力和实践能力.因此,结构不良问题设计要根据其特性,一方面对真实的情境进行适当地加工,使其蕴含着有价值的问题,期待学生从多个视角去发现、探究它;另一方面对条件、结论、方法等问题结构要素进行合理设置,或使条件部分呈现,或调用的概念、原理不明确,或解决方法多样.
同课章节目录
