回归概念 突出本质 彰显素养 ——新高考函数小题赏析和复习建议 课件(共62张PPT)
文档属性
| 名称 | 回归概念 突出本质 彰显素养 ——新高考函数小题赏析和复习建议 课件(共62张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 56.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-23 21:46:41 | ||
图片预览









文档简介
(共62张PPT)
回归概念 突出本质 彰显素养
——新高考函数小题赏析和复习建议
新高考函数小题试题特点
函数小题优秀试题赏析
函数复习和课堂教学建议
目
录
CONTENTS
新高考函数小题试题特点
目
录
CONTENTS
在熟悉的地方看风景:
近4年全国卷和三年新高考全国1卷怎么考?
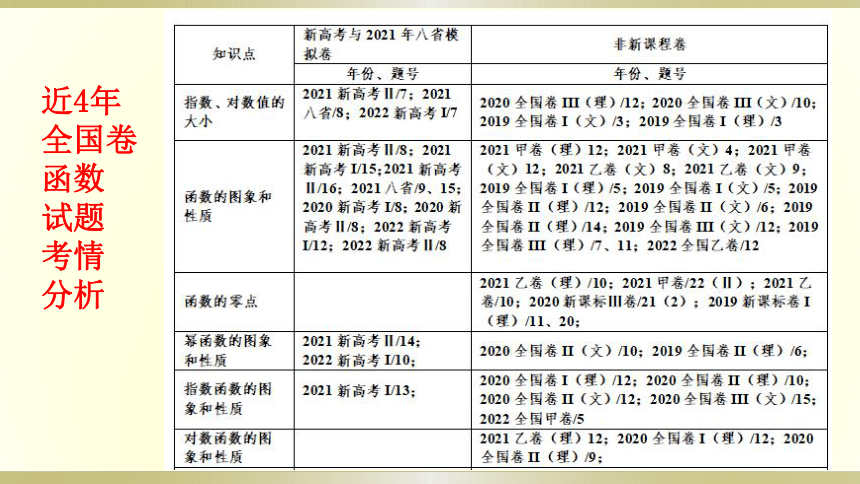
近4年
全国卷
函数
试题
考情
分析
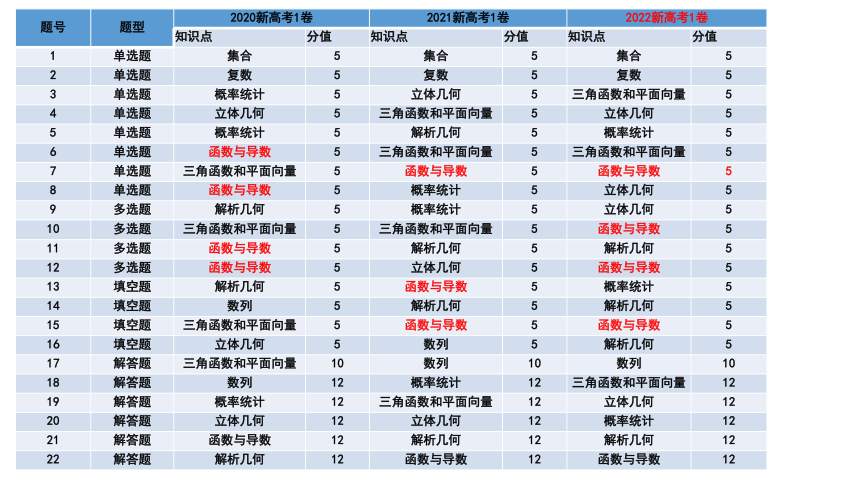
题号 题型 2020新高考1卷 2021新高考1卷 2022新高考1卷 知识点 分值 知识点 分值 知识点 分值
1 单选题 集合 5 集合 5 集合 5
2 单选题 复数 5 复数 5 复数 5
3 单选题 概率统计 5 立体几何 5 三角函数和平面向量 5
4 单选题 立体几何 5 三角函数和平面向量 5 立体几何 5
5 单选题 概率统计 5 解析几何 5 概率统计 5
6 单选题 函数与导数 5 三角函数和平面向量 5 三角函数和平面向量 5
7 单选题 三角函数和平面向量 5 函数与导数 5 函数与导数 5
8 单选题 函数与导数 5 概率统计 5 立体几何 5
9 多选题 解析几何 5 概率统计 5 立体几何 5
10 多选题 三角函数和平面向量 5 三角函数和平面向量 5 函数与导数 5
11 多选题 函数与导数 5 解析几何 5 解析几何 5
12 多选题 函数与导数 5 立体几何 5 函数与导数 5
13 填空题 解析几何 5 函数与导数 5 概率统计 5
14 填空题 数列 5 解析几何 5 解析几何 5
15 填空题 三角函数和平面向量 5 函数与导数 5 函数与导数 5
16 填空题 立体几何 5 数列 5 解析几何 5
17 解答题 三角函数和平面向量 10 数列 10 数列 10
18 解答题 数列 12 概率统计 12 三角函数和平面向量 12
19 解答题 概率统计 12 三角函数和平面向量 12 立体几何 12
20 解答题 立体几何 12 立体几何 12 概率统计 12
21 解答题 函数与导数 12 解析几何 12 解析几何 12
22 解答题 解析几何 12 函数与导数 12 函数与导数 12
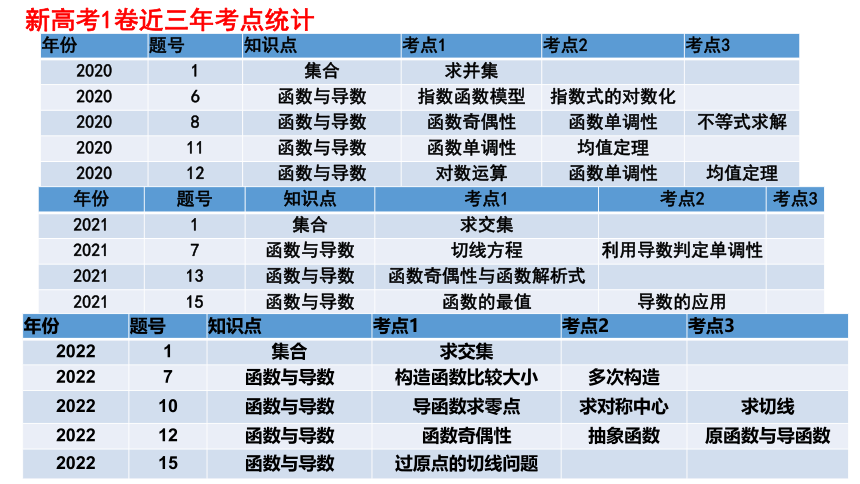
新高考1卷近三年考点统计
年份 题号 知识点 考点1 考点2 考点3
2020 1 集合 求并集
2020 6 函数与导数 指数函数模型 指数式的对数化
2020 8 函数与导数 函数奇偶性 函数单调性 不等式求解
2020 11 函数与导数 函数单调性 均值定理
2020 12 函数与导数 对数运算 函数单调性 均值定理
年份 题号 知识点 考点1 考点2 考点3
2021 1 集合 求交集
2021 7 函数与导数 切线方程 利用导数判定单调性
2021 13 函数与导数 函数奇偶性与函数解析式
2021 15 函数与导数 函数的最值 导数的应用
年份 题号 知识点 考点1 考点2 考点3
2022 1 集合 求交集
2022 7 函数与导数 构造函数比较大小 多次构造
2022 10 函数与导数 导函数求零点 求对称中心 求切线
2022 12 函数与导数 函数奇偶性 抽象函数 原函数与导函数
2022 15 函数与导数 过原点的切线问题
《普通高中数学课程标准》
《浙江省普通高中学科教学指导意见》
1.函数的概念及运算
2.函数性质 3.函数图像
4.三次函数 5.分段函数
6.抽象函数(宠上天)
7.比较大小(大红大紫)
8.函数零点 9.求参范围
10.切线
11.函数的极值最值
12.创新情境题
常考内容
三核心:
概念
图象
性质
思想方法与关键能力
数形结合思想
分类讨论思想
函数与方程思想
等价转化思想
数学抽象能力
数学运算能力
直观想象能力
逻辑推理能力
函数小题优秀试题赏析
目
录
CONTENTS
考点一:函数的概念与运算
视角:考查函数奇偶性概念的理解
定义域先行,x=-1时,
再用f(0)=0即可
例2 (1)[2021·全国乙卷] 设a≠0,若x=a为函数
f(x)=a(x-a)2(x-b)的极大值点,则( )
A.ab C.aba2
答案 D
视角一:求导+分类讨论
视角二:图象 寄穿偶回
视角三:极值的概念与本质
因为f(a)=0,所以当x无限接近与a时,f(a)<0
(1)所以a(a-b)<0,
浙江:a+b<0,所以b<-a
考点一:函数的概念与运算
视角:指对数运算
视角:设切点,二次方程判别式
纯数学使我们能够发现概念和联系这些概念的规律,这些概念和规律给了我们理解自然现象的钥匙 ——A.Einstein
考点二:函数性质
函数性质:主要考最值、单调性、奇偶性
视角:图象的特征
都是关于(0,1)对称
视角:奇偶性与单调性、解不等式相结合!
考点二:函数性质
视角:类周期+图象
视角:
两个函数都是关于x=1对称
所以f(1)=0
考点三:函数图像
解题策略:
从图象的差异着手,
看差异情况
奇偶性
单调性
特殊点
端点、极端情况
零点、极值点、正负
考点四:三次函数
三次函数的四种图象
考点四:三次函数
切割线性质
考点五:分段函数
视角:充分研究图象特征
考点六:抽象函数宠上天
微专题:抽象函数
微专题:抽象函数
一、 定义域问题
g(x)与h(x)有相同的值域
二、 解析式问题
三、 求值问题
待定系数法、换元法、拼凑法、赋值法、函数性质
赋值、求周期
四、 单调性、奇偶性
微专题:抽象函数
四、 单调性、奇偶性
与值域、不等式、恒成立相结合
考点六:抽象函数
有以下结论:
(1)若f(x+a)=-f(x),则T=2|a|; (2)若f(x+a)=, 则T=2|a|;
(3)若f(x+a)=f(x+b),则T=|a-b|.
五、 周期问题
例21(1) 已知函数f(x)满足f(x+3)=f(x),当x∈[0,2]时,f(x)=x2+4,则f(2022)= 4 .
(2)已知函数f(x)的定义域为R,对 x∈R,f(x+2)=-f(x)恒成立,且f(2)=5,则f(100)= (D )
A.10 B.5 C.0 D.-5
(3)已知定义在R上的函数f(x)满足f(x+2)=-,当x∈(0,2]时,f(x)=2x,则f(0)= ,f= .
-
2
考点六:抽象函数
五、 周期问题
视角一:也可以有赋值发现周期为6
视角二:找特殊函数
微专题:抽象函数
的图像关于x=2对称
为偶函数
典型错解
代数式的转化能力非常重要
视角一:从图象变换的角度
视角二:找特殊函数、画特殊图象理解(找三角函数)
视角三:利用定义
1.f(2-x)为偶函数,则f(x)的图像关于_____对称
2.f(2+3x)为偶函数,则f(x)的图像关于____对称
3.f(2+x)为奇函数,则f(x)的图像关于_____对称
4.f(2+3x)为奇函数,则f(x)的图像关于____对称
5.f(ax+b)为奇函数,则f(x)的图像关于____对称
5.f(ax+b)为奇函数,则f(b)=____
微专题:抽象函数
考点六:抽象函数
五、 周期问题
双对称
函数有周期
对称性与周期性之间的常用结论:
(1)若函数f(x)的图像关于直线x=a和x=b对称,则函数f(x)的周期T=2|b-a|;
(2)若函数f(x)的图像关于点(a,0)和点(b,0)对称,则函数f(x)的周期T=2|b-a|;
(3)若函数f(x)的图像关于直线x=a和点(b,0)对称,则函数f(x)的周期T=4|b-a|.
考点六:抽象函数
双对称
函数有周期
考点六:抽象函数
双对称
函数有周期
利用定义得出对称性
利用特殊函数理解
考点六:抽象函数
考点六:抽象函数
考点七:比较大小大红大紫
新高考函数不等关系问题的深度解析
——估值、不等式、构造函数、函数不等式
目标与方向
怎么构造函数?需要几个函数?
人教A版新教材必修第一册,p119第3题
解题视角:考查函数的单调性
回归原点
D
化归f(1/4)=f(4)
类似:ln2/2=ln4/4
视角一:估算
令z=2, x<5,y<3,所以5z最大;令y=2,x>3,2x>3y
视角二:不等式之作差法(商)
对数运算
例28
相遇高考,再见已是曲中人
D
视角三:指数函数图像
令x=1,
相遇高考,再见已是曲中人
A
D
视角一:对数运算、对数函数的单调性
视角二:构造函数
视角:对数运算、均值不等式、中间量
53>34,83<54
视角:构造函数,研究函数的单调性
相遇高考,再见已是曲中人
C
A
视角:放缩,构造函数,研究函数的单调性
相遇高考,再见已是曲中人
B
D
函数不等式的视角
重要不等式
例30
对数运算+均值不等式
A
相遇高考,再见已是曲中人
函数
增函数
学生视角:指数函数的增长速度快慢
重要不等式
例31
函数不等式的视角
A
估算法:正弦、余弦的泰勒展开
相遇高考,再见已是曲中人
例32
函数不等式的视角
估算
C
相遇高考,再见已是曲中人
极限法
构造函数
重要不等式
重要不等式
B
函数不等式的视角
相遇高考,再见已是曲中人
1.估值、代值、看变化规律
2、不等式
(作差(商)、对数运算、基本不等式、中间量)
3、构造函数(函数的单调性)
4、函数不等式(导数、泰勒展开)
函数中不等关系问题的解题视角
考点八:函数零点
考点八:函数零点
函数复习和课堂教学建议
目
录
CONTENTS
1.构建知识体系,不回避二级结论
2022新高考的几点思考
易中难题目配比由往年的6:3:1变为3:6:1,中档题大幅增加
善于思考,深入思考,并且勤奋,计算比较快而准确,思维敏捷的学霸会赚大便宜
非常勤奋重复刷题实际上却是思维上的“懒惰者”打回原形!
思维很活但是不愿意勤奋导致做题速度一般的学子狠狠地惩罚了一次,你不光要有思维,你还要勤奋!
为适应高考的学生画像:爱动脑筋,深入思考,在老师指导下形成知识网络,在脑海中有学科的整体框架和基本规律,平时会用所学知识,研究、探究一点小问题,考试时能应用所学知识解决问题。
课堂走的太快 成绩跟不上
学生说:老师都白教的
老师说:一届不如一届,学生越来越差
概念过得快 全靠刷题带
讲题不问出处 课堂炫耀套路
1.构建知识体系,不回避二级结论
“破题海”(盲目刷题、缺少反思总结不可取);
“破套路",(死记硬背题型生搬硬套方法不可取〕;
"破定势”(陈旧理念不更新不可取);
“破形式”(试题结构有没有可能不拘泥于现有的结构分布)
“四破”
2.重视通性通法,优化解题方法,提升思维能力
2.重视通性通法,优化解题方法,提升思维能力
2.重视通性通法,优化解题方法,提升思维能力
问题
概念与公式
图象与性质
怎样解题
通性通法
思想与方法
提升能力、积累经验、彰显素养
解决新问题
知识与本质
基于班级学生的实际精心设计教学内容
再识“五基”
基于班级学生的能力精准控制难度
基于班级学生的水平匹配课外作业
基于班级学生的状态调控课堂节奏
基于班级学生的知识漏洞定期微专题训练
3.精心设计课堂教学内容,因材施教
3.精心设计课堂教学内容,因材施教
看教师对高考方向、考点要求的把握水平
看教师组织调动学生积极性、主动性的水平
看教师在学情了解的基础上因材施教的水平
看教师课堂引导、讲解、归纳、提升的水平
看练习、周测、模考试题与高考对路的水平
“五看”
(1)从督促、检查、指导学生做好课堂笔记入手,抓好课堂的落实
(2)以个性化的作业布置”为抓下,提高课后作业的有效性
(3)从指导学生整理“错题档案”入手,逐步优化学生的知识结构
(4)以上好“试卷讲评课”为抓手,提高课堂的针对性与有效性
(5)以制定详细的 “讲价标准” 为抓手,規范学生的解題过程
(6)以题后反思”为抓手,引导学生善于思考、学会学习
“六落实”
4.狠抓落实,真实高效
讲必练:克服随意性
练必批:了解学生的真实水平与存在的问题
批必评:讲解具有针对性
评必纠:抓好落实
纠必考:内化学生的能力
对需要重点讲的考点或例习题(例题以中档综合题为重点,少选难题;尽量把近几年高考题选入,形成一个渐进技高的题组序列,满足各类学生的需要,分层推进),精心设计问题(起点低一点、坡度缓一点、分析细一点、难度小一点、板书过程规范严谨一点)巧妙创设思维情景,师生双向交流互动,发挥思维的互补性,让学生参与知识形成、问题解决、数学思想方法提炼的过程,给学生充足的时问独立思考和演练,以练带讲,以讲导练,充分发挥学生的主体作用,提高课堂实效:
4.狠抓落实,真实高效
2023,大家好运!
我们的使命:
给予学生一生的兴趣和研究问题的思维方式!
回归概念 突出本质 彰显素养
——新高考函数小题赏析和复习建议
新高考函数小题试题特点
函数小题优秀试题赏析
函数复习和课堂教学建议
目
录
CONTENTS
新高考函数小题试题特点
目
录
CONTENTS
在熟悉的地方看风景:
近4年全国卷和三年新高考全国1卷怎么考?
近4年
全国卷
函数
试题
考情
分析
题号 题型 2020新高考1卷 2021新高考1卷 2022新高考1卷 知识点 分值 知识点 分值 知识点 分值
1 单选题 集合 5 集合 5 集合 5
2 单选题 复数 5 复数 5 复数 5
3 单选题 概率统计 5 立体几何 5 三角函数和平面向量 5
4 单选题 立体几何 5 三角函数和平面向量 5 立体几何 5
5 单选题 概率统计 5 解析几何 5 概率统计 5
6 单选题 函数与导数 5 三角函数和平面向量 5 三角函数和平面向量 5
7 单选题 三角函数和平面向量 5 函数与导数 5 函数与导数 5
8 单选题 函数与导数 5 概率统计 5 立体几何 5
9 多选题 解析几何 5 概率统计 5 立体几何 5
10 多选题 三角函数和平面向量 5 三角函数和平面向量 5 函数与导数 5
11 多选题 函数与导数 5 解析几何 5 解析几何 5
12 多选题 函数与导数 5 立体几何 5 函数与导数 5
13 填空题 解析几何 5 函数与导数 5 概率统计 5
14 填空题 数列 5 解析几何 5 解析几何 5
15 填空题 三角函数和平面向量 5 函数与导数 5 函数与导数 5
16 填空题 立体几何 5 数列 5 解析几何 5
17 解答题 三角函数和平面向量 10 数列 10 数列 10
18 解答题 数列 12 概率统计 12 三角函数和平面向量 12
19 解答题 概率统计 12 三角函数和平面向量 12 立体几何 12
20 解答题 立体几何 12 立体几何 12 概率统计 12
21 解答题 函数与导数 12 解析几何 12 解析几何 12
22 解答题 解析几何 12 函数与导数 12 函数与导数 12
新高考1卷近三年考点统计
年份 题号 知识点 考点1 考点2 考点3
2020 1 集合 求并集
2020 6 函数与导数 指数函数模型 指数式的对数化
2020 8 函数与导数 函数奇偶性 函数单调性 不等式求解
2020 11 函数与导数 函数单调性 均值定理
2020 12 函数与导数 对数运算 函数单调性 均值定理
年份 题号 知识点 考点1 考点2 考点3
2021 1 集合 求交集
2021 7 函数与导数 切线方程 利用导数判定单调性
2021 13 函数与导数 函数奇偶性与函数解析式
2021 15 函数与导数 函数的最值 导数的应用
年份 题号 知识点 考点1 考点2 考点3
2022 1 集合 求交集
2022 7 函数与导数 构造函数比较大小 多次构造
2022 10 函数与导数 导函数求零点 求对称中心 求切线
2022 12 函数与导数 函数奇偶性 抽象函数 原函数与导函数
2022 15 函数与导数 过原点的切线问题
《普通高中数学课程标准》
《浙江省普通高中学科教学指导意见》
1.函数的概念及运算
2.函数性质 3.函数图像
4.三次函数 5.分段函数
6.抽象函数(宠上天)
7.比较大小(大红大紫)
8.函数零点 9.求参范围
10.切线
11.函数的极值最值
12.创新情境题
常考内容
三核心:
概念
图象
性质
思想方法与关键能力
数形结合思想
分类讨论思想
函数与方程思想
等价转化思想
数学抽象能力
数学运算能力
直观想象能力
逻辑推理能力
函数小题优秀试题赏析
目
录
CONTENTS
考点一:函数的概念与运算
视角:考查函数奇偶性概念的理解
定义域先行,x=-1时,
再用f(0)=0即可
例2 (1)[2021·全国乙卷] 设a≠0,若x=a为函数
f(x)=a(x-a)2(x-b)的极大值点,则( )
A.ab C.ab
答案 D
视角一:求导+分类讨论
视角二:图象 寄穿偶回
视角三:极值的概念与本质
因为f(a)=0,所以当x无限接近与a时,f(a)<0
(1)所以a(a-b)<0,
浙江:a+b<0,所以b<-a
考点一:函数的概念与运算
视角:指对数运算
视角:设切点,二次方程判别式
纯数学使我们能够发现概念和联系这些概念的规律,这些概念和规律给了我们理解自然现象的钥匙 ——A.Einstein
考点二:函数性质
函数性质:主要考最值、单调性、奇偶性
视角:图象的特征
都是关于(0,1)对称
视角:奇偶性与单调性、解不等式相结合!
考点二:函数性质
视角:类周期+图象
视角:
两个函数都是关于x=1对称
所以f(1)=0
考点三:函数图像
解题策略:
从图象的差异着手,
看差异情况
奇偶性
单调性
特殊点
端点、极端情况
零点、极值点、正负
考点四:三次函数
三次函数的四种图象
考点四:三次函数
切割线性质
考点五:分段函数
视角:充分研究图象特征
考点六:抽象函数宠上天
微专题:抽象函数
微专题:抽象函数
一、 定义域问题
g(x)与h(x)有相同的值域
二、 解析式问题
三、 求值问题
待定系数法、换元法、拼凑法、赋值法、函数性质
赋值、求周期
四、 单调性、奇偶性
微专题:抽象函数
四、 单调性、奇偶性
与值域、不等式、恒成立相结合
考点六:抽象函数
有以下结论:
(1)若f(x+a)=-f(x),则T=2|a|; (2)若f(x+a)=, 则T=2|a|;
(3)若f(x+a)=f(x+b),则T=|a-b|.
五、 周期问题
例21(1) 已知函数f(x)满足f(x+3)=f(x),当x∈[0,2]时,f(x)=x2+4,则f(2022)= 4 .
(2)已知函数f(x)的定义域为R,对 x∈R,f(x+2)=-f(x)恒成立,且f(2)=5,则f(100)= (D )
A.10 B.5 C.0 D.-5
(3)已知定义在R上的函数f(x)满足f(x+2)=-,当x∈(0,2]时,f(x)=2x,则f(0)= ,f= .
-
2
考点六:抽象函数
五、 周期问题
视角一:也可以有赋值发现周期为6
视角二:找特殊函数
微专题:抽象函数
的图像关于x=2对称
为偶函数
典型错解
代数式的转化能力非常重要
视角一:从图象变换的角度
视角二:找特殊函数、画特殊图象理解(找三角函数)
视角三:利用定义
1.f(2-x)为偶函数,则f(x)的图像关于_____对称
2.f(2+3x)为偶函数,则f(x)的图像关于____对称
3.f(2+x)为奇函数,则f(x)的图像关于_____对称
4.f(2+3x)为奇函数,则f(x)的图像关于____对称
5.f(ax+b)为奇函数,则f(x)的图像关于____对称
5.f(ax+b)为奇函数,则f(b)=____
微专题:抽象函数
考点六:抽象函数
五、 周期问题
双对称
函数有周期
对称性与周期性之间的常用结论:
(1)若函数f(x)的图像关于直线x=a和x=b对称,则函数f(x)的周期T=2|b-a|;
(2)若函数f(x)的图像关于点(a,0)和点(b,0)对称,则函数f(x)的周期T=2|b-a|;
(3)若函数f(x)的图像关于直线x=a和点(b,0)对称,则函数f(x)的周期T=4|b-a|.
考点六:抽象函数
双对称
函数有周期
考点六:抽象函数
双对称
函数有周期
利用定义得出对称性
利用特殊函数理解
考点六:抽象函数
考点六:抽象函数
考点七:比较大小大红大紫
新高考函数不等关系问题的深度解析
——估值、不等式、构造函数、函数不等式
目标与方向
怎么构造函数?需要几个函数?
人教A版新教材必修第一册,p119第3题
解题视角:考查函数的单调性
回归原点
D
化归f(1/4)=f(4)
类似:ln2/2=ln4/4
视角一:估算
令z=2, x<5,y<3,所以5z最大;令y=2,x>3,2x>3y
视角二:不等式之作差法(商)
对数运算
例28
相遇高考,再见已是曲中人
D
视角三:指数函数图像
令x=1,
相遇高考,再见已是曲中人
A
D
视角一:对数运算、对数函数的单调性
视角二:构造函数
视角:对数运算、均值不等式、中间量
53>34,83<54
视角:构造函数,研究函数的单调性
相遇高考,再见已是曲中人
C
A
视角:放缩,构造函数,研究函数的单调性
相遇高考,再见已是曲中人
B
D
函数不等式的视角
重要不等式
例30
对数运算+均值不等式
A
相遇高考,再见已是曲中人
函数
增函数
学生视角:指数函数的增长速度快慢
重要不等式
例31
函数不等式的视角
A
估算法:正弦、余弦的泰勒展开
相遇高考,再见已是曲中人
例32
函数不等式的视角
估算
C
相遇高考,再见已是曲中人
极限法
构造函数
重要不等式
重要不等式
B
函数不等式的视角
相遇高考,再见已是曲中人
1.估值、代值、看变化规律
2、不等式
(作差(商)、对数运算、基本不等式、中间量)
3、构造函数(函数的单调性)
4、函数不等式(导数、泰勒展开)
函数中不等关系问题的解题视角
考点八:函数零点
考点八:函数零点
函数复习和课堂教学建议
目
录
CONTENTS
1.构建知识体系,不回避二级结论
2022新高考的几点思考
易中难题目配比由往年的6:3:1变为3:6:1,中档题大幅增加
善于思考,深入思考,并且勤奋,计算比较快而准确,思维敏捷的学霸会赚大便宜
非常勤奋重复刷题实际上却是思维上的“懒惰者”打回原形!
思维很活但是不愿意勤奋导致做题速度一般的学子狠狠地惩罚了一次,你不光要有思维,你还要勤奋!
为适应高考的学生画像:爱动脑筋,深入思考,在老师指导下形成知识网络,在脑海中有学科的整体框架和基本规律,平时会用所学知识,研究、探究一点小问题,考试时能应用所学知识解决问题。
课堂走的太快 成绩跟不上
学生说:老师都白教的
老师说:一届不如一届,学生越来越差
概念过得快 全靠刷题带
讲题不问出处 课堂炫耀套路
1.构建知识体系,不回避二级结论
“破题海”(盲目刷题、缺少反思总结不可取);
“破套路",(死记硬背题型生搬硬套方法不可取〕;
"破定势”(陈旧理念不更新不可取);
“破形式”(试题结构有没有可能不拘泥于现有的结构分布)
“四破”
2.重视通性通法,优化解题方法,提升思维能力
2.重视通性通法,优化解题方法,提升思维能力
2.重视通性通法,优化解题方法,提升思维能力
问题
概念与公式
图象与性质
怎样解题
通性通法
思想与方法
提升能力、积累经验、彰显素养
解决新问题
知识与本质
基于班级学生的实际精心设计教学内容
再识“五基”
基于班级学生的能力精准控制难度
基于班级学生的水平匹配课外作业
基于班级学生的状态调控课堂节奏
基于班级学生的知识漏洞定期微专题训练
3.精心设计课堂教学内容,因材施教
3.精心设计课堂教学内容,因材施教
看教师对高考方向、考点要求的把握水平
看教师组织调动学生积极性、主动性的水平
看教师在学情了解的基础上因材施教的水平
看教师课堂引导、讲解、归纳、提升的水平
看练习、周测、模考试题与高考对路的水平
“五看”
(1)从督促、检查、指导学生做好课堂笔记入手,抓好课堂的落实
(2)以个性化的作业布置”为抓下,提高课后作业的有效性
(3)从指导学生整理“错题档案”入手,逐步优化学生的知识结构
(4)以上好“试卷讲评课”为抓手,提高课堂的针对性与有效性
(5)以制定详细的 “讲价标准” 为抓手,規范学生的解題过程
(6)以题后反思”为抓手,引导学生善于思考、学会学习
“六落实”
4.狠抓落实,真实高效
讲必练:克服随意性
练必批:了解学生的真实水平与存在的问题
批必评:讲解具有针对性
评必纠:抓好落实
纠必考:内化学生的能力
对需要重点讲的考点或例习题(例题以中档综合题为重点,少选难题;尽量把近几年高考题选入,形成一个渐进技高的题组序列,满足各类学生的需要,分层推进),精心设计问题(起点低一点、坡度缓一点、分析细一点、难度小一点、板书过程规范严谨一点)巧妙创设思维情景,师生双向交流互动,发挥思维的互补性,让学生参与知识形成、问题解决、数学思想方法提炼的过程,给学生充足的时问独立思考和演练,以练带讲,以讲导练,充分发挥学生的主体作用,提高课堂实效:
4.狠抓落实,真实高效
2023,大家好运!
我们的使命:
给予学生一生的兴趣和研究问题的思维方式!
同课章节目录
