2023届高考数学二轮复习常考二级结论理解记 课件(共40张PPT)
文档属性
| 名称 | 2023届高考数学二轮复习常考二级结论理解记 课件(共40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-28 18:17:29 | ||
图片预览










文档简介
(共40张PPT)
常考二级结论理解记
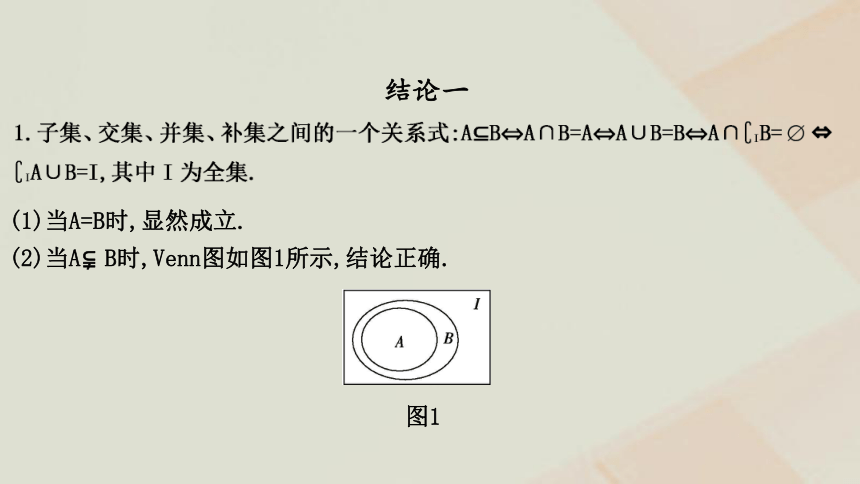
结论一
(1)当A=B时,显然成立.
(2)当A B时,Venn图如图1所示,结论正确.
图1
2.子集个数的问题:若一个集合A含有n(n∈N*)个元素,则集合A的子集有2n个,非空子集有2n-1个,真子集有2n-1个,非空真子集有2n-2个.
理解:A的子集有2n个,从每个元素的取舍来理解,例如每个元素都有两种选择,则n个元素共有2n种选择,该结论需要掌握并会灵活应用.
结论二
交、并、补(且、或、非)之间的关系在集合中的表达形式: I(A∩B)=( IA)∪
( IB), I(A∪B)=( IA)∩( IB).
结论三
奇函数的最值性质:已知函数f(x)是定义在区间D上的奇函数,则对任意的x∈D,都有f(x)+f(-x)=0.特别地,若奇函数f(x)在定义域Df上有最值,则f(x)max+
f(x)min=0,且若0∈Df,则f(0)=0.
证明:因为f(x)为奇函数,所以 x∈D,-x∈D,且f(-x)=-f(x),即f(x)+f(-x)=
0.若0∈Df,令x=0,则有f(0)+f(-0)=0,即f(0)=0.
若奇函数f(x)在Df上有最值,设f(x)max=f(x0),则f(x0)≥f(x)(x∈D),
所以f(-x0)=-f(x0)≤-f(x)(-x∈D),即f(x)min=f(-x0).
由f(x0)+f(-x0)=0,得f(x)max+f(x)min=0.
结论四
函数周期性问题:已知定义在R上的函数f(x),若对任意的x∈R,总存在非零常数T,使得f(x+T)=f(x),则称f(x)是周期函数,T为一个周期.
除周期函数的定义外,还有一些常见的与周期函数有关的结论如下:
(1)如果f(x+a)=-f(x)(a≠0),那么f(x)是周期函数,其中的一个周期T=2a.
(3)如果f(x+a)+f(x)=c(a≠0),那么f(x)是周期函数,其中的一个周期T=2a.
(4)如果f(x)=f(x+a)+f(x-a)(a≠0),那么f(x)是周期函数,其中的一个周期T=6a.
结论五
复合函数单调性:已知函数y=f[g(x)]是定义在D上的函数,若f(x)与g(x)的单调性相同,则y=f[g(x)]在D上单调递增;若f(x)与g(x)的单调性相反,则y=
f[g(x)]在D上单调递减,即“同增异减”.特别地,若f(x)是定义在D上的单调函数,且方程f[f(x)]=x在D上有解为x0,则f(x0)=x0.
结论六
1.二次函数解析式的三种表达式:
2.二次函数f(x)=ax2+bx+c(a≠0)的性质:
(4)抛物线y=f(x)与y轴的交点为(0,c).
结论七
“切线”不等式:
(1)对数形式:ln(x+1)≤x(x>-1),当且仅当x=0时,取等号.
x (-1,0) 0 (0,+∞)
f′(x) + 0 -
f(x) ↗ 极大值 ↘
所以f(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,且当x=0时,f(x)有最大值为0,即 x>-1,ln(x+1)-x≤f(0)=0,所以ln(x+1)≤x(x>-1)恒成立,当且仅当x=0时,取等号.
“切线”不等式:
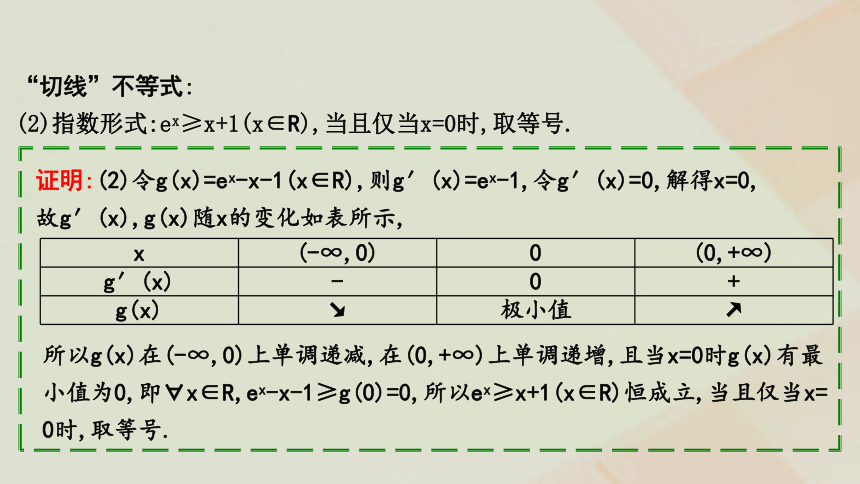
(2)指数形式:ex≥x+1(x∈R),当且仅当x=0时,取等号.
证明:(2)令g(x)=ex-x-1(x∈R),则g′(x)=ex-1,令g′(x)=0,解得x=0,
故g′(x),g(x)随x的变化如表所示,
x (-∞,0) 0 (0,+∞)
g′(x) - 0 +
g(x) ↘ 极小值 ↗
所以g(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,且当x=0时g(x)有最小值为0,即 x∈R,ex-x-1≥g(0)=0,所以ex≥x+1(x∈R)恒成立,当且仅当x=
0时,取等号.
结论八
函数的对称性:已知函数f(x)是定义在R上的函数.
结论九
图2
结论十
图3
图4
结论十一
结论十二
1.已知等差数列{an}的前n项和为Sn,等比数列{bn}的前n项积为Tn,m,n,t∈N*.
结论十三
已知等比数列{an},其公比为q(q≠0),前n项和为Sn.
(2)若q=1,则Sn=na1,且{an}同时为等差数列.
结论十四
已知数列{an}的前n项和为Sn,前n项积为Tn.
(1)若{an}为等差数列,公差为d,则Sn,S2n-Sn,S3n-S2n,…仍为等差数列,公差为n2d.
(2)若{an}为等比数列,公比为q(q≠0),则Sn,S2n-Sn,S3n-S2n,…仍为等比数列(当n为偶数时,q≠-1),公比为qn.
结论十五
1.已知圆O的方程为(x-m)2+(y-n)2=R2,点P(a,b),直线l:(a-m)(x-m)+(b-n)(y-n)=R2.
(1)若点P在圆O上,则直线l与圆O相切,点P为切点,l为切线.
(2)若点P在圆O外,则直线l与圆O相交,两交点分别为过点P作圆的两切线的切
点,l为切点弦所在的直线.
(3)若点P在圆O内(不是圆心),则直线l与圆O相离,圆心到直线l的距离d满足R2=|OP|·d.
2.过圆或圆锥曲线上一点P(x0,y0)的切线方程.
(1)过圆C:(x-a)2+(y-b)2=R2上一点P(x0,y0)的切线方程为(x0-a)(x-a)+(y0-b)·(y-b)=R2.
(3)过抛物线C:y2=2px(p>0)上一点P(x0,y0)的切线方程为y0y=p(x+x0).
3.已知点M(x0,y0),抛物线C:y2=2px(p>0)和直线l:y0y=p(x+x0).
(1)当点M在抛物线C上时,直线l与抛物线C相切,其中点M为切点,l为切线.
(2)当点M在抛物线C外时,直线l与抛物线C相交,其中两交点与点M的连线分别是抛物线的切线,即直线l为切点弦所在的直线.
(3)当点M在抛物线C内时,直线l与抛物线C相离.
理解:(1)求过圆锥曲线上(或外)一点的切线方程时,可以借助直线与圆锥曲线的位置关系的解题套路(联立方程,看判别式).
(2)在求过圆外一点P(x0,y0)的圆的切线方程时,应注意理解如下两点:①所求切线一定有两条;②设直线方程之前,应对所求直线的斜率是否存在加以讨论.
结论十六
图5
图6
图7
图8
结论十七
在圆锥曲线(椭圆、双曲线、抛物线)中,曲线上的一定点P(非顶点)与曲线上的两动点A,B满足直线PA与直线PB的斜率互为相反数(倾斜角互补),则直线AB的斜率为定值.
图9
图10
图11
下面以双曲线为例给出证明.
结论十八
若圆锥曲线中内接直角三角线的直角顶点与圆锥曲线的顶点重合,则斜边所在直线过定点.具体结论及证明如下:
图12
结论十九
(1)如图13所示,以AB为直径的圆与准线l相切于点E.
图13
(2)如图14所示,以A1B1为直径的圆与弦AB相切于点F,且|EF|2=|AA1|·|BB1|.
图14
(3)如图15所示,以AF为直径的圆与y轴相切.
图15
结论二十
焦点三角形的面积:
图16
(2)双曲线相关结论的证明略.
常考二级结论理解记
结论一
(1)当A=B时,显然成立.
(2)当A B时,Venn图如图1所示,结论正确.
图1
2.子集个数的问题:若一个集合A含有n(n∈N*)个元素,则集合A的子集有2n个,非空子集有2n-1个,真子集有2n-1个,非空真子集有2n-2个.
理解:A的子集有2n个,从每个元素的取舍来理解,例如每个元素都有两种选择,则n个元素共有2n种选择,该结论需要掌握并会灵活应用.
结论二
交、并、补(且、或、非)之间的关系在集合中的表达形式: I(A∩B)=( IA)∪
( IB), I(A∪B)=( IA)∩( IB).
结论三
奇函数的最值性质:已知函数f(x)是定义在区间D上的奇函数,则对任意的x∈D,都有f(x)+f(-x)=0.特别地,若奇函数f(x)在定义域Df上有最值,则f(x)max+
f(x)min=0,且若0∈Df,则f(0)=0.
证明:因为f(x)为奇函数,所以 x∈D,-x∈D,且f(-x)=-f(x),即f(x)+f(-x)=
0.若0∈Df,令x=0,则有f(0)+f(-0)=0,即f(0)=0.
若奇函数f(x)在Df上有最值,设f(x)max=f(x0),则f(x0)≥f(x)(x∈D),
所以f(-x0)=-f(x0)≤-f(x)(-x∈D),即f(x)min=f(-x0).
由f(x0)+f(-x0)=0,得f(x)max+f(x)min=0.
结论四
函数周期性问题:已知定义在R上的函数f(x),若对任意的x∈R,总存在非零常数T,使得f(x+T)=f(x),则称f(x)是周期函数,T为一个周期.
除周期函数的定义外,还有一些常见的与周期函数有关的结论如下:
(1)如果f(x+a)=-f(x)(a≠0),那么f(x)是周期函数,其中的一个周期T=2a.
(3)如果f(x+a)+f(x)=c(a≠0),那么f(x)是周期函数,其中的一个周期T=2a.
(4)如果f(x)=f(x+a)+f(x-a)(a≠0),那么f(x)是周期函数,其中的一个周期T=6a.
结论五
复合函数单调性:已知函数y=f[g(x)]是定义在D上的函数,若f(x)与g(x)的单调性相同,则y=f[g(x)]在D上单调递增;若f(x)与g(x)的单调性相反,则y=
f[g(x)]在D上单调递减,即“同增异减”.特别地,若f(x)是定义在D上的单调函数,且方程f[f(x)]=x在D上有解为x0,则f(x0)=x0.
结论六
1.二次函数解析式的三种表达式:
2.二次函数f(x)=ax2+bx+c(a≠0)的性质:
(4)抛物线y=f(x)与y轴的交点为(0,c).
结论七
“切线”不等式:
(1)对数形式:ln(x+1)≤x(x>-1),当且仅当x=0时,取等号.
x (-1,0) 0 (0,+∞)
f′(x) + 0 -
f(x) ↗ 极大值 ↘
所以f(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,且当x=0时,f(x)有最大值为0,即 x>-1,ln(x+1)-x≤f(0)=0,所以ln(x+1)≤x(x>-1)恒成立,当且仅当x=0时,取等号.
“切线”不等式:
(2)指数形式:ex≥x+1(x∈R),当且仅当x=0时,取等号.
证明:(2)令g(x)=ex-x-1(x∈R),则g′(x)=ex-1,令g′(x)=0,解得x=0,
故g′(x),g(x)随x的变化如表所示,
x (-∞,0) 0 (0,+∞)
g′(x) - 0 +
g(x) ↘ 极小值 ↗
所以g(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,且当x=0时g(x)有最小值为0,即 x∈R,ex-x-1≥g(0)=0,所以ex≥x+1(x∈R)恒成立,当且仅当x=
0时,取等号.
结论八
函数的对称性:已知函数f(x)是定义在R上的函数.
结论九
图2
结论十
图3
图4
结论十一
结论十二
1.已知等差数列{an}的前n项和为Sn,等比数列{bn}的前n项积为Tn,m,n,t∈N*.
结论十三
已知等比数列{an},其公比为q(q≠0),前n项和为Sn.
(2)若q=1,则Sn=na1,且{an}同时为等差数列.
结论十四
已知数列{an}的前n项和为Sn,前n项积为Tn.
(1)若{an}为等差数列,公差为d,则Sn,S2n-Sn,S3n-S2n,…仍为等差数列,公差为n2d.
(2)若{an}为等比数列,公比为q(q≠0),则Sn,S2n-Sn,S3n-S2n,…仍为等比数列(当n为偶数时,q≠-1),公比为qn.
结论十五
1.已知圆O的方程为(x-m)2+(y-n)2=R2,点P(a,b),直线l:(a-m)(x-m)+(b-n)(y-n)=R2.
(1)若点P在圆O上,则直线l与圆O相切,点P为切点,l为切线.
(2)若点P在圆O外,则直线l与圆O相交,两交点分别为过点P作圆的两切线的切
点,l为切点弦所在的直线.
(3)若点P在圆O内(不是圆心),则直线l与圆O相离,圆心到直线l的距离d满足R2=|OP|·d.
2.过圆或圆锥曲线上一点P(x0,y0)的切线方程.
(1)过圆C:(x-a)2+(y-b)2=R2上一点P(x0,y0)的切线方程为(x0-a)(x-a)+(y0-b)·(y-b)=R2.
(3)过抛物线C:y2=2px(p>0)上一点P(x0,y0)的切线方程为y0y=p(x+x0).
3.已知点M(x0,y0),抛物线C:y2=2px(p>0)和直线l:y0y=p(x+x0).
(1)当点M在抛物线C上时,直线l与抛物线C相切,其中点M为切点,l为切线.
(2)当点M在抛物线C外时,直线l与抛物线C相交,其中两交点与点M的连线分别是抛物线的切线,即直线l为切点弦所在的直线.
(3)当点M在抛物线C内时,直线l与抛物线C相离.
理解:(1)求过圆锥曲线上(或外)一点的切线方程时,可以借助直线与圆锥曲线的位置关系的解题套路(联立方程,看判别式).
(2)在求过圆外一点P(x0,y0)的圆的切线方程时,应注意理解如下两点:①所求切线一定有两条;②设直线方程之前,应对所求直线的斜率是否存在加以讨论.
结论十六
图5
图6
图7
图8
结论十七
在圆锥曲线(椭圆、双曲线、抛物线)中,曲线上的一定点P(非顶点)与曲线上的两动点A,B满足直线PA与直线PB的斜率互为相反数(倾斜角互补),则直线AB的斜率为定值.
图9
图10
图11
下面以双曲线为例给出证明.
结论十八
若圆锥曲线中内接直角三角线的直角顶点与圆锥曲线的顶点重合,则斜边所在直线过定点.具体结论及证明如下:
图12
结论十九
(1)如图13所示,以AB为直径的圆与准线l相切于点E.
图13
(2)如图14所示,以A1B1为直径的圆与弦AB相切于点F,且|EF|2=|AA1|·|BB1|.
图14
(3)如图15所示,以AF为直径的圆与y轴相切.
图15
结论二十
焦点三角形的面积:
图16
(2)双曲线相关结论的证明略.
同课章节目录
