四川省宣汉县第二中学(新课标人教版)高三数学复习《简易逻辑》
文档属性
| 名称 | 四川省宣汉县第二中学(新课标人教版)高三数学复习《简易逻辑》 |  | |
| 格式 | zip | ||
| 文件大小 | 73.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-18 08:02:11 | ||
图片预览

文档简介
简易逻辑
一、逻辑联结词
【知识体系】
命题:可以判断真假的语句叫做命题。其中判断为真的语句叫做真命题,判断为假的语句叫做假命题;
逻辑联结词:“或” “且” “非”这些词叫做逻辑联结词;
简单命题与复合命题:不含逻辑联结词的命题叫做简单命题;由简单命题与逻辑联结词构成的命题叫做复合命题;
复合命题的构成形式:p且q,p或q,非p;
真值表:
p q p且q p或q 非p
真 真 真 真 假
真 假 假 真 假
假 真 假 真 真
假 假 假 假 真
例1:已知命题方程有两个不相等的负数根;方程无实根.若“或”为真,“且”为假,求实数的取值范围。
二、四种命题
【知识体系】
1、四种命题:一般地,用p和q分别表示原命题的条件和结论,用┐p和┐q分别表示p和q的否定。于是四种命题的形式为:
原命题:
逆命题:
否命题:
逆否命题:
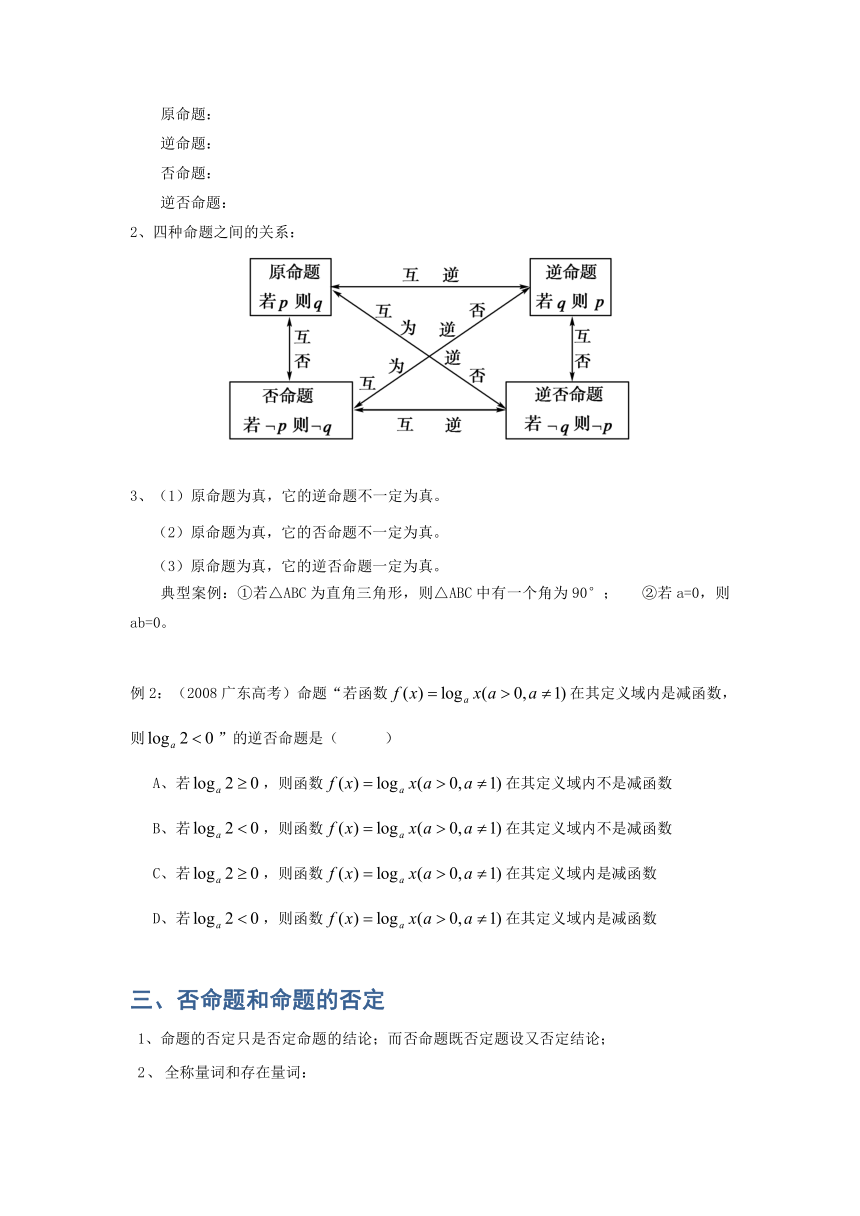
四种命题之间的关系:
(1)原命题为真,它的逆命题不一定为真。
(2)原命题为真,它的否命题不一定为真。
(3)原命题为真,它的逆否命题一定为真。
典型案例:①若△ABC为直角三角形,则△ABC中有一个角为90°; ②若a=0,则ab=0。
例2:(2008广东高考)命题“若函数在其定义域内是减函数,则”的逆否命题是( )
A、若,则函数在其定义域内不是减函数
B、若,则函数在其定义域内不是减函数
C、若,则函数在其定义域内是减函数
D、若,则函数在其定义域内是减函数
三、否命题和命题的否定
命题的否定只是否定命题的结论;而否命题既否定题设又否定结论;
全称量词和存在量词:
(1)全称量词:“一切”、“任意”、“所有”、“凡是”等词,用符号“”表示。
(2)存在量词:“存在一个”、“至少有一个”等词,用符号“”表示。
全称命题和特称命题:含有全称量词的命题是全称命题,含有存在量词的命题是特称命题。
注:全称命题的否定是特称命题,特称命题的否定是全称命题。
例3:写出命题:“若,则”的否定与否命题,并加以区别。
例4:命题“对任意,都有”的否命题是什么?
五、充要条件
【知识体系】
充分条件:若,则p是q的充分条件;
必要条件:若,则q是p的必要条件;
充要条件:若且,则p和q互为充要条件。
例5:(2008安徽卷)是方程至少有一个负数根的( )
必要不充分条件 B.充分不必要条件 C.充分必要条件 D.既不充分也不必要条件
例6:(2008湖北卷)若集合,则:( )
A. 是的充分条件,不是的必要条件
B. 不是的充分条件,是的必要条件
C是的充分条件,又是的必要条件.
D.既不是的充分条件,又不是的必要条件
例7:已知p:|1-|≤2,q:x2-2x+1-m2≤0(m>0),若p是q的必要而不充分条件,求实数m的取值范围.
答案部分
1.答案:真假:
假真:
答案:A
答案:否定:若,则
否命题:若,则
命题的否定式不否题设,只否结论
否命题是题设和结论都否定
答案:,
答案:B
答案:B
7.答案:
一、逻辑联结词
【知识体系】
命题:可以判断真假的语句叫做命题。其中判断为真的语句叫做真命题,判断为假的语句叫做假命题;
逻辑联结词:“或” “且” “非”这些词叫做逻辑联结词;
简单命题与复合命题:不含逻辑联结词的命题叫做简单命题;由简单命题与逻辑联结词构成的命题叫做复合命题;
复合命题的构成形式:p且q,p或q,非p;
真值表:
p q p且q p或q 非p
真 真 真 真 假
真 假 假 真 假
假 真 假 真 真
假 假 假 假 真
例1:已知命题方程有两个不相等的负数根;方程无实根.若“或”为真,“且”为假,求实数的取值范围。
二、四种命题
【知识体系】
1、四种命题:一般地,用p和q分别表示原命题的条件和结论,用┐p和┐q分别表示p和q的否定。于是四种命题的形式为:
原命题:
逆命题:
否命题:
逆否命题:
四种命题之间的关系:
(1)原命题为真,它的逆命题不一定为真。
(2)原命题为真,它的否命题不一定为真。
(3)原命题为真,它的逆否命题一定为真。
典型案例:①若△ABC为直角三角形,则△ABC中有一个角为90°; ②若a=0,则ab=0。
例2:(2008广东高考)命题“若函数在其定义域内是减函数,则”的逆否命题是( )
A、若,则函数在其定义域内不是减函数
B、若,则函数在其定义域内不是减函数
C、若,则函数在其定义域内是减函数
D、若,则函数在其定义域内是减函数
三、否命题和命题的否定
命题的否定只是否定命题的结论;而否命题既否定题设又否定结论;
全称量词和存在量词:
(1)全称量词:“一切”、“任意”、“所有”、“凡是”等词,用符号“”表示。
(2)存在量词:“存在一个”、“至少有一个”等词,用符号“”表示。
全称命题和特称命题:含有全称量词的命题是全称命题,含有存在量词的命题是特称命题。
注:全称命题的否定是特称命题,特称命题的否定是全称命题。
例3:写出命题:“若,则”的否定与否命题,并加以区别。
例4:命题“对任意,都有”的否命题是什么?
五、充要条件
【知识体系】
充分条件:若,则p是q的充分条件;
必要条件:若,则q是p的必要条件;
充要条件:若且,则p和q互为充要条件。
例5:(2008安徽卷)是方程至少有一个负数根的( )
必要不充分条件 B.充分不必要条件 C.充分必要条件 D.既不充分也不必要条件
例6:(2008湖北卷)若集合,则:( )
A. 是的充分条件,不是的必要条件
B. 不是的充分条件,是的必要条件
C是的充分条件,又是的必要条件.
D.既不是的充分条件,又不是的必要条件
例7:已知p:|1-|≤2,q:x2-2x+1-m2≤0(m>0),若p是q的必要而不充分条件,求实数m的取值范围.
答案部分
1.答案:真假:
假真:
答案:A
答案:否定:若,则
否命题:若,则
命题的否定式不否题设,只否结论
否命题是题设和结论都否定
答案:,
答案:B
答案:B
7.答案:
同课章节目录
