四川省宣汉县第二中学(新课标人教版)高三数学复习《立体几何》
文档属性
| 名称 | 四川省宣汉县第二中学(新课标人教版)高三数学复习《立体几何》 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-18 08:03:49 | ||
图片预览


文档简介
简单几何体
柱体
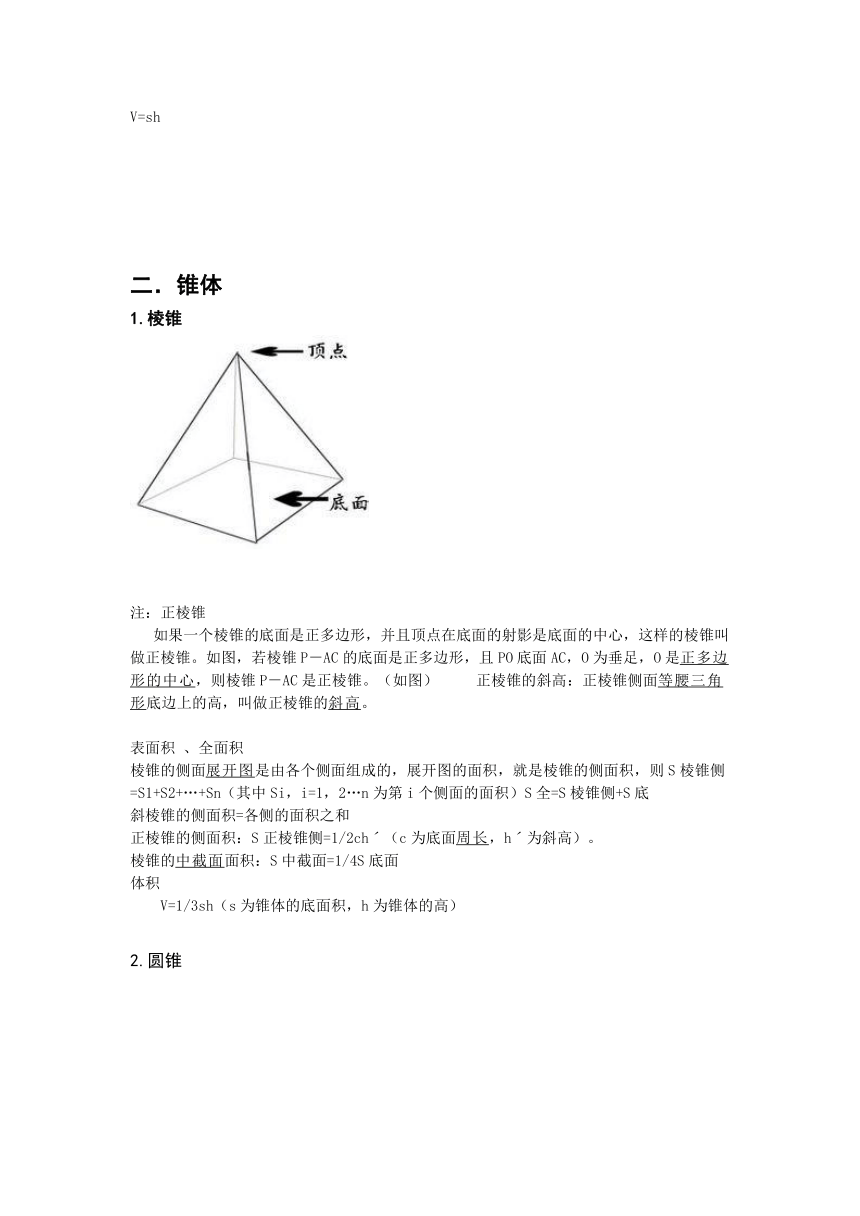
棱柱
棱柱的底面可以是三角形,四边形,五边形……我们把这样的棱柱叫分别叫做三棱柱、四棱柱、五棱柱……
2)按侧棱与底面是否垂直分为:直棱柱、斜棱柱,直棱柱按底面是不是正多边形分为:正棱柱、其他直棱柱。
侧面积
S=ch(直),S=cl(斜/c:直截面周长,l:斜棱长)
体积:
V=sh
圆柱
表面积
S=ch+两个底面积
侧面积
S=ch
体积
V=sh
锥体
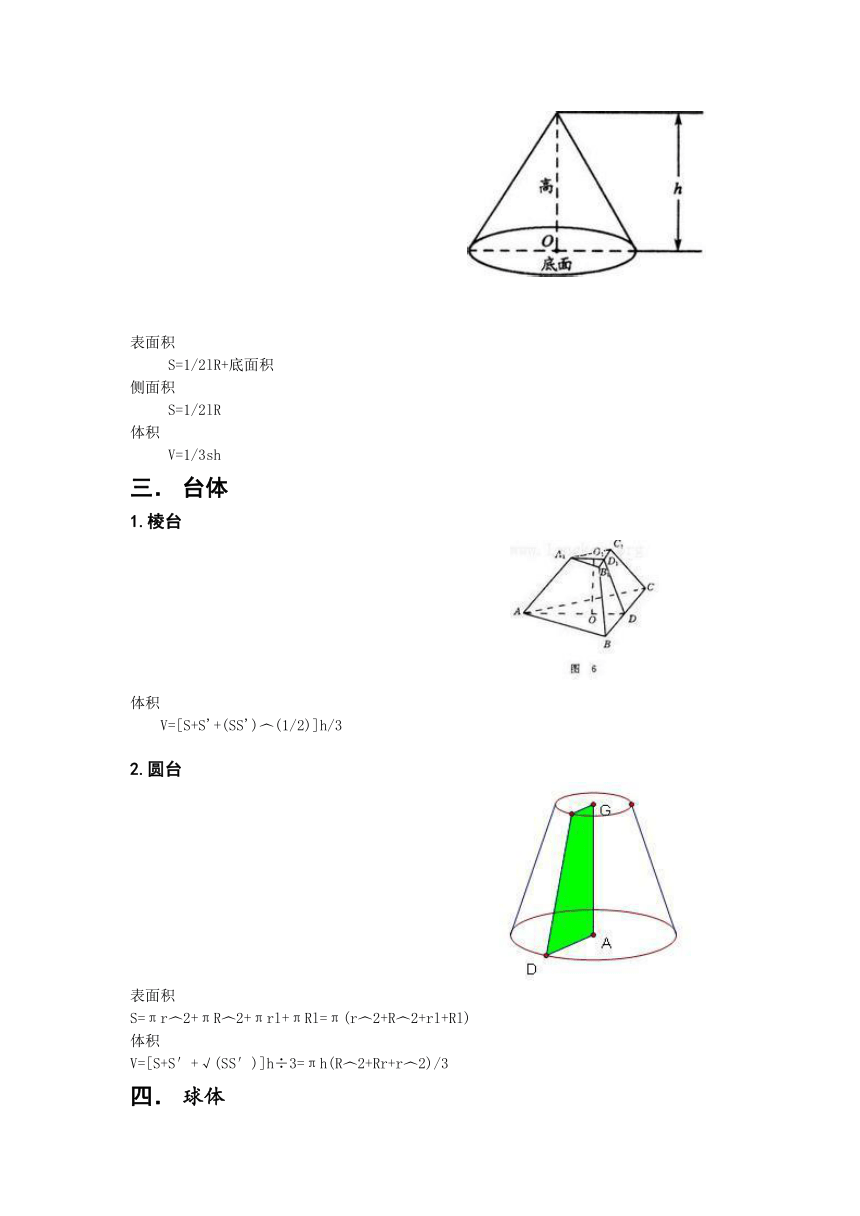
棱锥
注:正棱锥
如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥。如图,若棱锥P-AC的底面是正多边形,且PO底面AC,O为垂足,O是正多边形的中心 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ),则棱锥P-AC是正棱锥。(如图) 正棱锥的斜高:正棱锥侧面等腰三角形底边上的高,叫做正棱锥的斜高 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )。
表面积 、全面积
棱锥的侧面展开图是由各个侧面组成的,展开图的面积,就是棱锥的侧面积,则S棱锥侧=S1+S2+…+Sn(其中Si,i=1,2…n为第i个侧面的面积)S全=S棱锥侧+S底
斜棱锥的侧面积=各侧的面积之和
正棱锥的侧面积:S正棱锥侧=1/2chˊ(c为底面周长 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ),hˊ为斜高)。
棱锥的中截面面积:S中截面=1/4S底面
体积
V=1/3sh(s为锥体的底面积,h为锥体的高)
圆锥
表面积
S=1/2lR+底面积
侧面积
S=1/2lR
体积
V=1/3sh
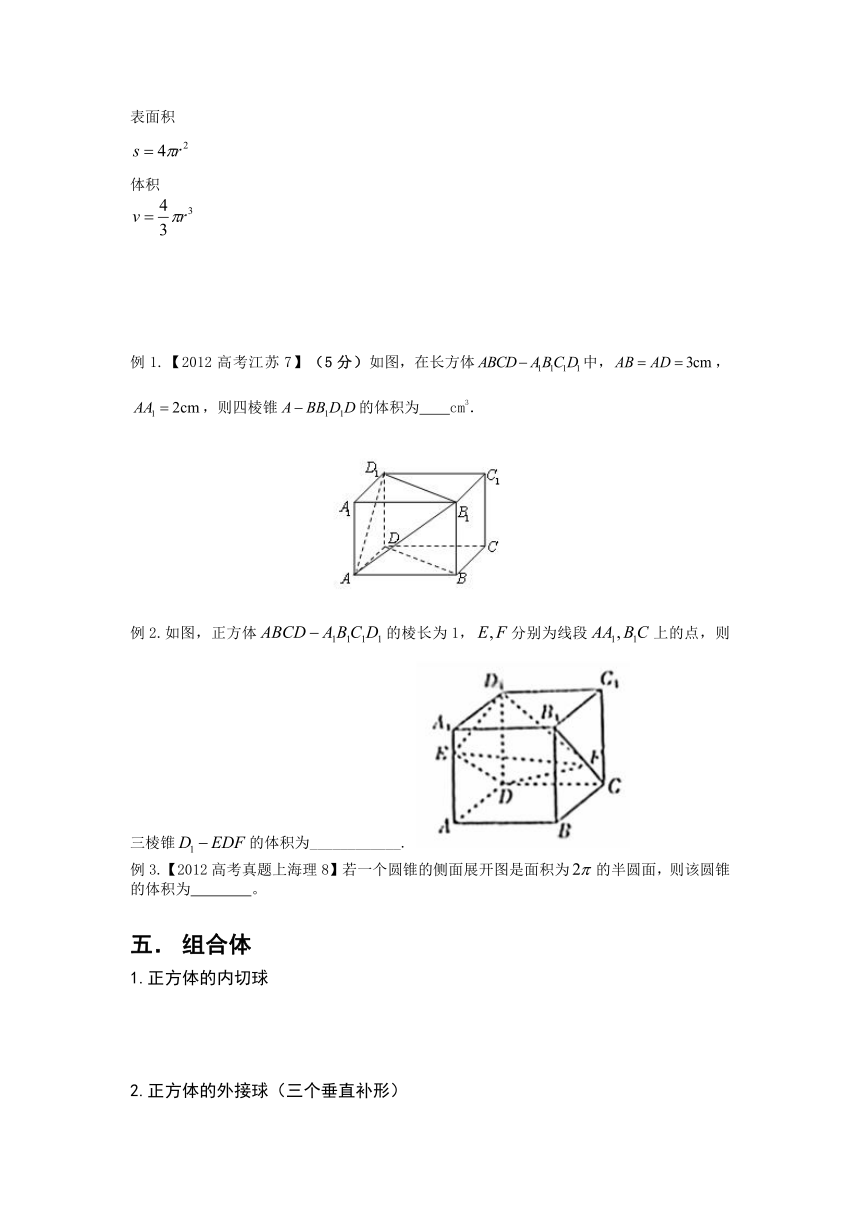
台体
1.棱台
体积
V=[S+S'+(SS')︿(1/2)]h/3
2.圆台
表面积
S=πr︿2+πR︿2+πrl+πRl=π(r︿2+R︿2+rl+Rl)
体积
V=[S+S′+√(SS′)]h÷3=πh(R︿2+Rr+r︿2)/3
球体
表面积
体积
例1.【2012高考江苏7】(5分)如图,在长方体中,,,则四棱锥的体积为 cm3.
例2.如图,正方体的棱长为1,分别为线段上的点,则三棱锥的体积为____________.
例3.【2012高考真题上海理8】若一个圆锥的侧面展开图是面积为的半圆面,则该圆锥的体积为 。
组合体
正方体的内切球
正方体的外接球(三个垂直补形)
长方体的外接球
正三棱柱内切球的半径
正三棱柱外接球的半径(两个垂直做三角形)
正四面体的内切球
正四面体的外接球
例1.【2012高考真题辽宁16】已知正三棱锥ABC,点P,A,B,C都在半径为的求面上,若PA,PB,PC两两互相垂直,则球心到截面ABC的距离为________。
例2.【2012高考新课标文8】平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为
(A)π (B)4π (C)4π (D)6π
例3.【2012高考真题新课标理11】已知三棱锥的所有顶点都在球的求面上,是边长为的正三角形,为球的直径,且;则此棱锥的体积为( )
例4.(重庆9)高为的四棱锥S-ABCD的底面是边长为1的正方形,点S、A、B、C、D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为
A. B. C.1 D.
例5.(全国大纲11)已知平面α截一球面得圆M,过圆心M且与α成二面角的平面β截该球面得圆N.若该球面的半径为4,圆M的面积为4,则圆N的面积为
A.7 B.9 C.11 D.13
例6.已知球的直径SC=4,A,B是该球球面上的两点,AB=,,则棱锥S—ABC的体积为
(A) (B) (C) (D)1
例7.(2010辽宁文数)(11)已知是球表面上的点,,,,,则球的表面积等于
(A)4 (B)3 (C)2 (D)
例8.(2009四川卷文)如图,在半径为3的球面上有三点,=90°,,
球心O到平面的距离是,则两点的球面距离是
A. B.
C. D.2
例9.【2012高考辽宁文16】已知点P,A,B,C,D是球O表面上的点,PA⊥平面ABCD,四边形ABCD是边长为2正方形。若PA=2,则△OAB的面积为______________.
立体几何三视图
从直观图判断三视图
例题:(08广东)将正三棱柱截去三个角(如图甲所示A,B,C分别是三边的中点)得到几何体如图乙,则该几何体按图乙所示方向的侧视图(或称左视图)为( )
例1、(07山东)下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A、① ② B、① ③ C、① ④ D、② ④
例2、如图,水平放置的三棱柱的侧棱长和底面边长均为2,且侧棱平面,正视图是边长为2的正方形,该三棱柱的左视图的面积为( )
A、4 B、 C、 D、
例3、如图是一个正三棱柱的直观图,若其左视图的面积等于其俯视图的面积,且主视图的面积等于4,则该三棱柱的体积等于( )
B、 C、 D、
例4.【2012高考陕西文8】将正方形(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为 ( )
从三视图还原直观图并求该体的表面积体积等
例1:某几何体的三视图如图所示,那么这个几何体是( )
三棱锥 B、四棱锥 C、四棱台 D、三棱台
例2:用小立方体搭成一个几何体,使它的主视图和俯视图如图所示、搭建这样的几何体,需要小立方体的块数的最大值与最小值分别是( )
A、17 1l B、16 11 C、15 10 D、15 11
例3:用若干个大小相同,棱长为l的正方体摆成一个立体模型,其三视图如下:
则此立体模型的体积为( )
A、4 B、5 C、6 D、7
例4、已知一几何体的三视图如图所示,试画出它的直观图,则它的体积为______________(说明:画直观图时,对尺寸比例不作严格要求)。
例5、(07海、宁卷)已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
cm3 B、cm3 C、cm3 D、cm3
例6、一个几何体的三视图如图所示,则其体积等于( )
A、 B、 C、 D、
空间点线面位置关系
一.三个公理:
公理一:如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
公理二:过不在一条直线上的三点,有且只有一个平面。
公理三:如果两个不重合的平面有一个公共点,那么他们有且只有一条过该公共点的公共直线。
证明点共线
例:
证明线共面
例:
点与线的位置关系
点与面的位置关系
线与线的位置关系
线与面的位置关系
面与面的位置关系
空间几何-------平行、垂直
一.“平行关系”常见证明方法
(一)直线与直线平行的证明
利用某些平面图形的特性:如平行四边形的对边互相平行
利用三角形中位线性质
利用空间平行线的传递性(即公理4):
平行于同一条直线的两条直线互相平行。
利用直线与平面平行的性质定理:
如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
利用平面与平面平行的性质定理:
如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
利用直线与平面垂直的性质定理:
垂直于同一个平面的两条直线互相平行。
利用平面内直线与直线垂直的性质:
在同一个平面内,垂直于同一条直线的两条直线互相平行。
利用定义:在同一个平面内且两条直线没有公共点
(二)直线与平面平行的证明
利用直线与平面平行的判定定理:
平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行。
利用平面与平面平行的性质推论:
两个平面互相平行,则其中一个平面内的任一直线平行于另一个平面。
利用定义:直线在平面外,且直线与平面没有公共点
(二)平面与平面平行的证明
常见证明方法:
利用平面与平面平行的判定定理:
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
利用某些空间几何体的特性:如正方体的上下底面互相平行等
利用定义:两个平面没有公共点
三、“垂直关系”常见证明方法
(一)直线与直线垂直的证明
利用某些平面图形的特性:如直角三角形的两条直角边互相垂直等。
看夹角:两条共(异)面直线的夹角为90°,则两直线互相垂直。
利用直线与平面垂直的性质:
如果一条直线与一个平面垂直,则这条直线垂直于此平面内的所有直线。
利用平面与平面垂直的性质推论:
如果两个平面互相垂直,在这两个平面内分别作垂直于交线的直线,则这两条直线互相垂直。
利用常用结论:
如果两条直线互相平行,且其中一条直线垂直于第三条直线,则另一条直线也垂直于第三条直线。
如果有一条直线垂直于一个平面,另一条直线平行于此平面,那么这两条直线互相垂直。
(二)直线与平面垂直的证明
利用某些空间几何体的特性:如长方体侧棱垂直于底面等
看直线与平面所成的角:如果直线与平面所成的角是直角,则这条直线垂直于此平面。
利用直线与平面垂直的判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线垂直于此平面。
利用平面与平面垂直的性质定理:
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
利用常用结论:
一条直线平行于一个平面的一条垂线,则该直线也垂直于此平面。
两个平面平行,一直线垂直于其中一个平面,则该直线也垂直于另一个平面。
(三)平面与平面垂直的证明
利用某些空间几何体的特性:如长方体侧面垂直于底面等
看二面角:两个平面相交,如果它们所成的二面角是直二面角(即平面角是直角的二面角),就说这连个平面互相垂直。
利用平面与平面垂直的判定定理
一个平面过另一个平面的垂线,则这两个平面垂直。
例1.下列命题正确的是( )
A、若两条直线和同一个平面所成的角相等,则这两条直线平行
B、若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行
C、若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行
D、若两个平面都垂直于第三个平面,则这两个平面平行
例2. 设是直线,a,β是两个不同的平面
A. 若∥a,∥β,则a∥β B. 若∥a,⊥β,则a⊥β
C. 若a⊥β,⊥a,则⊥β D. 若a⊥β, ∥a,则⊥β
例3.设两条异面直线l、m外一点p,下面说法正确的是( )
过P点能做无数条直线与l、m平行
B.过p点有且只有一条直线与l、m平行
C.过P点有且只有一条直线与l、m垂直
D.过p点有且只有一条直线与l、m相交
例4、(2009年福建卷理7)设m,n是平面α内的两条不同直线,,是平面β内的两条相交直线,则α//β的一个充分而不必要条件是( )
A、m//β且//α B、m//且n//
C、m//β且n//β D、m//β且n//
例5、(2009年江苏卷理12)设α和β为不重合的两个平面,给出下列命题:
(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;
(2)若α外一条直线l与α内的一条直线平行,则l和α平行;
(3)设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;
(4)直线l与α垂直的充分必要条件是l与α内的两条直线垂直。
上面命题中,真命题的序号_________________(写出所有真命题的序号)。
例6、(2008年天津卷理4)设a,b是两条直线,α,β是两个平面,则a⊥b的一个充分条件是( )
A、a⊥α,b∥β,α⊥β B、a⊥α, b⊥β,α∥β
C、a α,b⊥β,α∥β D、a α,b∥β,α⊥β
例7、(2007年江苏卷理4)已知两条直线m,n,两个平面α,β,给出下面四个命题:
①m//n,m⊥α n⊥α
②α//β,m α,n β m//n
③m//n,m//α n//α
④α//β,m//n,m⊥α n⊥β
其中正确命题的序号是
A、①、③ B、②、④ C、①、④ D、②、③
例8、(2007年辽宁卷理7)若m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中的真命题是( )
A、若m β,α⊥β,则m⊥α
B、若α∩γ=m,β∩γ=n,m∥n,则α∥β
C、若m⊥β,m∥α,则α⊥β
D、若α⊥γ,α⊥β,则β⊥γ
解答题
例1.如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点
(I)证明:平面BDC1⊥平面BDC
(Ⅱ)平面BDC1分此棱柱为两部分,求这两部分体积的比.
例2.如图6,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形, AD∥BC,AC⊥BD.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
例5.如图,几何体是四棱锥,△为正三角形,.
(Ⅰ)求证:;
(Ⅱ)若∠,M为线段AE的中点,
求证:∥平面.
例6.如图5所示,在四棱锥中,平面,,,是的中点,是上的点且,为△中边上的高.
(1)证明:平面;
(2)若,,,求三棱
锥的体积;
(3)证明:平面.
例7.【2102高考北京文16】(本小题共14分)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2。
(I)求证:DE∥平面A1CB;
(II)求证:A1F⊥BE;
(III)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由。
例8.直三棱柱ABC- A1B1C1中,AB=A A1 ,=
(Ⅰ)证明;
(Ⅱ)已知AB=2,BC=,求三棱锥 的体积
例9.【2012高考辽宁文18】(本小题满分12分)
如图,直三棱柱,,AA′=1,点M,N分别为和的中点。
(Ⅰ)证明:∥平面;
(Ⅱ)求三棱锥的体积。
(椎体体积公式V=Sh,其中S为地面面积,h为高)
简单几何体答案
例1.【答案】6。
【考点】正方形的性质,棱锥的体积。
【解析】∵长方体底面是正方形,∴△中 cm,边上的高是cm(它也是中上的高)。
∴四棱锥的体积为。
例2.【答案】
【解析】法一:因为点在线段上,所以,又因为点在线段上,所以点到平面的距离为1,即,所以.
法二:使用特殊点的位置进行求解,不失一般性令点在点处,点在点处,则。
例3.【答案】
【解析】因为半圆面的面积为,所以,即,即圆锥的母线为,底面圆的周长,所以圆锥的底面半径,所以圆锥的高,所以圆锥的体积为。
组合体:
例1.【答案】
例2.【答案】B
【解析】球半径,所以球的体积为,选B.
3.【答案】A
【解析】的外接圆的半径,点到面的距离,为球的直径点到面的距离为此棱锥的体积为
另:排除,选A.
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】
【解析】时,
,则
8.解析:选A.由已知,球的直径为,表面积为
9.【答案】B
【解析】∵AC是小圆的直径。所以过球心O作小圆的垂线,垂足O’是AC的中点。
O’C=,AC=3,∴BC=3,即BC=OB=OC。∴
,则两点的球面距离=
三视图:
A 2.D 3.B 4.D 5.B
1.B 2.A 3.B 4. 5.B 6.B
平行垂直:
1.【答案】C
【解析】A.两直线可能平行,相交,异面故A不正确;B.两平面平行或相交;C.正确;D.这两个平面平行或相交.
2.【答案】B
【解析】利用排除法可得选项B是正确的,∵∥a,⊥β,则a⊥β.如选项A:∥a,∥β时,a⊥β或a∥β;选项C:若a⊥β,⊥a,∥β或;选项D:若若a⊥β, ⊥a,∥β或⊥β.
3.C 4.B 5.(1).(2) 6.B 7.C 8.C
解答题:
1.【答案】
2.【答案】
【解析】(Ⅰ)因为
又是平面PAC内的两条相较直线,所以BD平面PAC,
而平面PAC,所以.
(Ⅱ)设AC和BD相交于点O,连接PO,由(Ⅰ)知,BD平面PAC,
所以是直线PD和平面PAC所成的角,从而.
由BD平面PAC,平面PAC,知.
在中,由,得PD=2OD.
因为四边形ABCD为等腰梯形,,所以均为等腰直角三角形,
从而梯形ABCD的高为于是梯形ABCD面积
在等腰三角形AOD中,
所以
故四棱锥的体积为.
【点评】本题考查空间直线垂直关系的证明,考查空间角的应用,及几何体体积计算.第一问只要证明BD平面PAC即可,第二问由(Ⅰ)知,BD平面PAC,所以是直线PD和平面PAC所成的角,然后算出梯形的面积和棱锥的高,由算得体积.
3.
【点评】本题以三棱柱为载体主要考查空间中的线面平行的判定,借助空间直角坐标系求平面的法向量的方法,并利用法向量判定平面的垂直关系,考查空间想象能力、推理论证能力、运算求解能力,难度适中。第一小题可以通过线线平行来证明线面平行,也可通过面面平行来证明。
4.【答案】(1)在中,
得:
同理:
得:面
(2)面
取的中点,过点作于点,连接
,面面面
得:点与点重合
且是二面角的平面角
设,则,
既二面角的大小为
5.【答案】(19)(I)设中点为O,连接OC,OE,则由知 ,,
又已知,所以平面OCE.
所以,即OE是BD的垂直平分线,
所以.
(II)取AB中点N,连接,
∵M是AE的中点,∴∥,
∵△是等边三角形,∴.
由∠BCD=120°知,∠CBD=30°,所以∠ABC=60°+30°=90°,即,
所以ND∥BC,
所以平面MND∥平面BEC,故DM∥平面BEC.
【解析】(1)证明:因为平面,
所以。
因为为△中边上的高,
所以。
因为,
所以平面。
(2)连结,取中点,连结。
因为是的中点,
所以。
因为平面,
所以平面。
则,
。
(3)证明:取中点,连结,。
因为是的中点,
所以。
因为,
所以,
所以四边形是平行四边形,
所以。
因为,
所以。
因为平面,
所以。
因为,
所以平面,
所以平面。
6. 【答案】
7.【答案】
8.【答案】
【解析】本题以三棱柱为载体主要考查空间中的线面平行的判定、棱锥体积的计算,考查空间想象能力、推理论证能力、运算求解能力,难度适中。第一小题可以通过线线平行来证明线面平行,也可通过面面平行来证明;第二小题求体积根据条件选择合适的底面是关键,也可以采用割补发来球体积。
b
α
β
β
α
a
P
α
b
b
β
α
c
b
b
α
C
B
A
D
C1
A1
柱体
棱柱
棱柱的底面可以是三角形,四边形,五边形……我们把这样的棱柱叫分别叫做三棱柱、四棱柱、五棱柱……
2)按侧棱与底面是否垂直分为:直棱柱、斜棱柱,直棱柱按底面是不是正多边形分为:正棱柱、其他直棱柱。
侧面积
S=ch(直),S=cl(斜/c:直截面周长,l:斜棱长)
体积:
V=sh
圆柱
表面积
S=ch+两个底面积
侧面积
S=ch
体积
V=sh
锥体
棱锥
注:正棱锥
如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥。如图,若棱锥P-AC的底面是正多边形,且PO底面AC,O为垂足,O是正多边形的中心 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ),则棱锥P-AC是正棱锥。(如图) 正棱锥的斜高:正棱锥侧面等腰三角形底边上的高,叫做正棱锥的斜高 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )。
表面积 、全面积
棱锥的侧面展开图是由各个侧面组成的,展开图的面积,就是棱锥的侧面积,则S棱锥侧=S1+S2+…+Sn(其中Si,i=1,2…n为第i个侧面的面积)S全=S棱锥侧+S底
斜棱锥的侧面积=各侧的面积之和
正棱锥的侧面积:S正棱锥侧=1/2chˊ(c为底面周长 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ),hˊ为斜高)。
棱锥的中截面面积:S中截面=1/4S底面
体积
V=1/3sh(s为锥体的底面积,h为锥体的高)
圆锥
表面积
S=1/2lR+底面积
侧面积
S=1/2lR
体积
V=1/3sh
台体
1.棱台
体积
V=[S+S'+(SS')︿(1/2)]h/3
2.圆台
表面积
S=πr︿2+πR︿2+πrl+πRl=π(r︿2+R︿2+rl+Rl)
体积
V=[S+S′+√(SS′)]h÷3=πh(R︿2+Rr+r︿2)/3
球体
表面积
体积
例1.【2012高考江苏7】(5分)如图,在长方体中,,,则四棱锥的体积为 cm3.
例2.如图,正方体的棱长为1,分别为线段上的点,则三棱锥的体积为____________.
例3.【2012高考真题上海理8】若一个圆锥的侧面展开图是面积为的半圆面,则该圆锥的体积为 。
组合体
正方体的内切球
正方体的外接球(三个垂直补形)
长方体的外接球
正三棱柱内切球的半径
正三棱柱外接球的半径(两个垂直做三角形)
正四面体的内切球
正四面体的外接球
例1.【2012高考真题辽宁16】已知正三棱锥ABC,点P,A,B,C都在半径为的求面上,若PA,PB,PC两两互相垂直,则球心到截面ABC的距离为________。
例2.【2012高考新课标文8】平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为
(A)π (B)4π (C)4π (D)6π
例3.【2012高考真题新课标理11】已知三棱锥的所有顶点都在球的求面上,是边长为的正三角形,为球的直径,且;则此棱锥的体积为( )
例4.(重庆9)高为的四棱锥S-ABCD的底面是边长为1的正方形,点S、A、B、C、D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为
A. B. C.1 D.
例5.(全国大纲11)已知平面α截一球面得圆M,过圆心M且与α成二面角的平面β截该球面得圆N.若该球面的半径为4,圆M的面积为4,则圆N的面积为
A.7 B.9 C.11 D.13
例6.已知球的直径SC=4,A,B是该球球面上的两点,AB=,,则棱锥S—ABC的体积为
(A) (B) (C) (D)1
例7.(2010辽宁文数)(11)已知是球表面上的点,,,,,则球的表面积等于
(A)4 (B)3 (C)2 (D)
例8.(2009四川卷文)如图,在半径为3的球面上有三点,=90°,,
球心O到平面的距离是,则两点的球面距离是
A. B.
C. D.2
例9.【2012高考辽宁文16】已知点P,A,B,C,D是球O表面上的点,PA⊥平面ABCD,四边形ABCD是边长为2正方形。若PA=2,则△OAB的面积为______________.
立体几何三视图
从直观图判断三视图
例题:(08广东)将正三棱柱截去三个角(如图甲所示A,B,C分别是三边的中点)得到几何体如图乙,则该几何体按图乙所示方向的侧视图(或称左视图)为( )
例1、(07山东)下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A、① ② B、① ③ C、① ④ D、② ④
例2、如图,水平放置的三棱柱的侧棱长和底面边长均为2,且侧棱平面,正视图是边长为2的正方形,该三棱柱的左视图的面积为( )
A、4 B、 C、 D、
例3、如图是一个正三棱柱的直观图,若其左视图的面积等于其俯视图的面积,且主视图的面积等于4,则该三棱柱的体积等于( )
B、 C、 D、
例4.【2012高考陕西文8】将正方形(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为 ( )
从三视图还原直观图并求该体的表面积体积等
例1:某几何体的三视图如图所示,那么这个几何体是( )
三棱锥 B、四棱锥 C、四棱台 D、三棱台
例2:用小立方体搭成一个几何体,使它的主视图和俯视图如图所示、搭建这样的几何体,需要小立方体的块数的最大值与最小值分别是( )
A、17 1l B、16 11 C、15 10 D、15 11
例3:用若干个大小相同,棱长为l的正方体摆成一个立体模型,其三视图如下:
则此立体模型的体积为( )
A、4 B、5 C、6 D、7
例4、已知一几何体的三视图如图所示,试画出它的直观图,则它的体积为______________(说明:画直观图时,对尺寸比例不作严格要求)。
例5、(07海、宁卷)已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
cm3 B、cm3 C、cm3 D、cm3
例6、一个几何体的三视图如图所示,则其体积等于( )
A、 B、 C、 D、
空间点线面位置关系
一.三个公理:
公理一:如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
公理二:过不在一条直线上的三点,有且只有一个平面。
公理三:如果两个不重合的平面有一个公共点,那么他们有且只有一条过该公共点的公共直线。
证明点共线
例:
证明线共面
例:
点与线的位置关系
点与面的位置关系
线与线的位置关系
线与面的位置关系
面与面的位置关系
空间几何-------平行、垂直
一.“平行关系”常见证明方法
(一)直线与直线平行的证明
利用某些平面图形的特性:如平行四边形的对边互相平行
利用三角形中位线性质
利用空间平行线的传递性(即公理4):
平行于同一条直线的两条直线互相平行。
利用直线与平面平行的性质定理:
如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
利用平面与平面平行的性质定理:
如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
利用直线与平面垂直的性质定理:
垂直于同一个平面的两条直线互相平行。
利用平面内直线与直线垂直的性质:
在同一个平面内,垂直于同一条直线的两条直线互相平行。
利用定义:在同一个平面内且两条直线没有公共点
(二)直线与平面平行的证明
利用直线与平面平行的判定定理:
平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行。
利用平面与平面平行的性质推论:
两个平面互相平行,则其中一个平面内的任一直线平行于另一个平面。
利用定义:直线在平面外,且直线与平面没有公共点
(二)平面与平面平行的证明
常见证明方法:
利用平面与平面平行的判定定理:
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
利用某些空间几何体的特性:如正方体的上下底面互相平行等
利用定义:两个平面没有公共点
三、“垂直关系”常见证明方法
(一)直线与直线垂直的证明
利用某些平面图形的特性:如直角三角形的两条直角边互相垂直等。
看夹角:两条共(异)面直线的夹角为90°,则两直线互相垂直。
利用直线与平面垂直的性质:
如果一条直线与一个平面垂直,则这条直线垂直于此平面内的所有直线。
利用平面与平面垂直的性质推论:
如果两个平面互相垂直,在这两个平面内分别作垂直于交线的直线,则这两条直线互相垂直。
利用常用结论:
如果两条直线互相平行,且其中一条直线垂直于第三条直线,则另一条直线也垂直于第三条直线。
如果有一条直线垂直于一个平面,另一条直线平行于此平面,那么这两条直线互相垂直。
(二)直线与平面垂直的证明
利用某些空间几何体的特性:如长方体侧棱垂直于底面等
看直线与平面所成的角:如果直线与平面所成的角是直角,则这条直线垂直于此平面。
利用直线与平面垂直的判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线垂直于此平面。
利用平面与平面垂直的性质定理:
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
利用常用结论:
一条直线平行于一个平面的一条垂线,则该直线也垂直于此平面。
两个平面平行,一直线垂直于其中一个平面,则该直线也垂直于另一个平面。
(三)平面与平面垂直的证明
利用某些空间几何体的特性:如长方体侧面垂直于底面等
看二面角:两个平面相交,如果它们所成的二面角是直二面角(即平面角是直角的二面角),就说这连个平面互相垂直。
利用平面与平面垂直的判定定理
一个平面过另一个平面的垂线,则这两个平面垂直。
例1.下列命题正确的是( )
A、若两条直线和同一个平面所成的角相等,则这两条直线平行
B、若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行
C、若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行
D、若两个平面都垂直于第三个平面,则这两个平面平行
例2. 设是直线,a,β是两个不同的平面
A. 若∥a,∥β,则a∥β B. 若∥a,⊥β,则a⊥β
C. 若a⊥β,⊥a,则⊥β D. 若a⊥β, ∥a,则⊥β
例3.设两条异面直线l、m外一点p,下面说法正确的是( )
过P点能做无数条直线与l、m平行
B.过p点有且只有一条直线与l、m平行
C.过P点有且只有一条直线与l、m垂直
D.过p点有且只有一条直线与l、m相交
例4、(2009年福建卷理7)设m,n是平面α内的两条不同直线,,是平面β内的两条相交直线,则α//β的一个充分而不必要条件是( )
A、m//β且//α B、m//且n//
C、m//β且n//β D、m//β且n//
例5、(2009年江苏卷理12)设α和β为不重合的两个平面,给出下列命题:
(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;
(2)若α外一条直线l与α内的一条直线平行,则l和α平行;
(3)设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;
(4)直线l与α垂直的充分必要条件是l与α内的两条直线垂直。
上面命题中,真命题的序号_________________(写出所有真命题的序号)。
例6、(2008年天津卷理4)设a,b是两条直线,α,β是两个平面,则a⊥b的一个充分条件是( )
A、a⊥α,b∥β,α⊥β B、a⊥α, b⊥β,α∥β
C、a α,b⊥β,α∥β D、a α,b∥β,α⊥β
例7、(2007年江苏卷理4)已知两条直线m,n,两个平面α,β,给出下面四个命题:
①m//n,m⊥α n⊥α
②α//β,m α,n β m//n
③m//n,m//α n//α
④α//β,m//n,m⊥α n⊥β
其中正确命题的序号是
A、①、③ B、②、④ C、①、④ D、②、③
例8、(2007年辽宁卷理7)若m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中的真命题是( )
A、若m β,α⊥β,则m⊥α
B、若α∩γ=m,β∩γ=n,m∥n,则α∥β
C、若m⊥β,m∥α,则α⊥β
D、若α⊥γ,α⊥β,则β⊥γ
解答题
例1.如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点
(I)证明:平面BDC1⊥平面BDC
(Ⅱ)平面BDC1分此棱柱为两部分,求这两部分体积的比.
例2.如图6,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形, AD∥BC,AC⊥BD.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
例5.如图,几何体是四棱锥,△为正三角形,.
(Ⅰ)求证:;
(Ⅱ)若∠,M为线段AE的中点,
求证:∥平面.
例6.如图5所示,在四棱锥中,平面,,,是的中点,是上的点且,为△中边上的高.
(1)证明:平面;
(2)若,,,求三棱
锥的体积;
(3)证明:平面.
例7.【2102高考北京文16】(本小题共14分)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2。
(I)求证:DE∥平面A1CB;
(II)求证:A1F⊥BE;
(III)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由。
例8.直三棱柱ABC- A1B1C1中,AB=A A1 ,=
(Ⅰ)证明;
(Ⅱ)已知AB=2,BC=,求三棱锥 的体积
例9.【2012高考辽宁文18】(本小题满分12分)
如图,直三棱柱,,AA′=1,点M,N分别为和的中点。
(Ⅰ)证明:∥平面;
(Ⅱ)求三棱锥的体积。
(椎体体积公式V=Sh,其中S为地面面积,h为高)
简单几何体答案
例1.【答案】6。
【考点】正方形的性质,棱锥的体积。
【解析】∵长方体底面是正方形,∴△中 cm,边上的高是cm(它也是中上的高)。
∴四棱锥的体积为。
例2.【答案】
【解析】法一:因为点在线段上,所以,又因为点在线段上,所以点到平面的距离为1,即,所以.
法二:使用特殊点的位置进行求解,不失一般性令点在点处,点在点处,则。
例3.【答案】
【解析】因为半圆面的面积为,所以,即,即圆锥的母线为,底面圆的周长,所以圆锥的底面半径,所以圆锥的高,所以圆锥的体积为。
组合体:
例1.【答案】
例2.【答案】B
【解析】球半径,所以球的体积为,选B.
3.【答案】A
【解析】的外接圆的半径,点到面的距离,为球的直径点到面的距离为此棱锥的体积为
另:排除,选A.
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】
【解析】时,
,则
8.解析:选A.由已知,球的直径为,表面积为
9.【答案】B
【解析】∵AC是小圆的直径。所以过球心O作小圆的垂线,垂足O’是AC的中点。
O’C=,AC=3,∴BC=3,即BC=OB=OC。∴
,则两点的球面距离=
三视图:
A 2.D 3.B 4.D 5.B
1.B 2.A 3.B 4. 5.B 6.B
平行垂直:
1.【答案】C
【解析】A.两直线可能平行,相交,异面故A不正确;B.两平面平行或相交;C.正确;D.这两个平面平行或相交.
2.【答案】B
【解析】利用排除法可得选项B是正确的,∵∥a,⊥β,则a⊥β.如选项A:∥a,∥β时,a⊥β或a∥β;选项C:若a⊥β,⊥a,∥β或;选项D:若若a⊥β, ⊥a,∥β或⊥β.
3.C 4.B 5.(1).(2) 6.B 7.C 8.C
解答题:
1.【答案】
2.【答案】
【解析】(Ⅰ)因为
又是平面PAC内的两条相较直线,所以BD平面PAC,
而平面PAC,所以.
(Ⅱ)设AC和BD相交于点O,连接PO,由(Ⅰ)知,BD平面PAC,
所以是直线PD和平面PAC所成的角,从而.
由BD平面PAC,平面PAC,知.
在中,由,得PD=2OD.
因为四边形ABCD为等腰梯形,,所以均为等腰直角三角形,
从而梯形ABCD的高为于是梯形ABCD面积
在等腰三角形AOD中,
所以
故四棱锥的体积为.
【点评】本题考查空间直线垂直关系的证明,考查空间角的应用,及几何体体积计算.第一问只要证明BD平面PAC即可,第二问由(Ⅰ)知,BD平面PAC,所以是直线PD和平面PAC所成的角,然后算出梯形的面积和棱锥的高,由算得体积.
3.
【点评】本题以三棱柱为载体主要考查空间中的线面平行的判定,借助空间直角坐标系求平面的法向量的方法,并利用法向量判定平面的垂直关系,考查空间想象能力、推理论证能力、运算求解能力,难度适中。第一小题可以通过线线平行来证明线面平行,也可通过面面平行来证明。
4.【答案】(1)在中,
得:
同理:
得:面
(2)面
取的中点,过点作于点,连接
,面面面
得:点与点重合
且是二面角的平面角
设,则,
既二面角的大小为
5.【答案】(19)(I)设中点为O,连接OC,OE,则由知 ,,
又已知,所以平面OCE.
所以,即OE是BD的垂直平分线,
所以.
(II)取AB中点N,连接,
∵M是AE的中点,∴∥,
∵△是等边三角形,∴.
由∠BCD=120°知,∠CBD=30°,所以∠ABC=60°+30°=90°,即,
所以ND∥BC,
所以平面MND∥平面BEC,故DM∥平面BEC.
【解析】(1)证明:因为平面,
所以。
因为为△中边上的高,
所以。
因为,
所以平面。
(2)连结,取中点,连结。
因为是的中点,
所以。
因为平面,
所以平面。
则,
。
(3)证明:取中点,连结,。
因为是的中点,
所以。
因为,
所以,
所以四边形是平行四边形,
所以。
因为,
所以。
因为平面,
所以。
因为,
所以平面,
所以平面。
6. 【答案】
7.【答案】
8.【答案】
【解析】本题以三棱柱为载体主要考查空间中的线面平行的判定、棱锥体积的计算,考查空间想象能力、推理论证能力、运算求解能力,难度适中。第一小题可以通过线线平行来证明线面平行,也可通过面面平行来证明;第二小题求体积根据条件选择合适的底面是关键,也可以采用割补发来球体积。
b
α
β
β
α
a
P
α
b
b
β
α
c
b
b
α
C
B
A
D
C1
A1
同课章节目录
