四川省宣汉县第二中学(新课标人教版)高三数学复习《抛物线》
文档属性
| 名称 | 四川省宣汉县第二中学(新课标人教版)高三数学复习《抛物线》 |  | |
| 格式 | zip | ||
| 文件大小 | 71.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-18 08:04:34 | ||
图片预览


文档简介
抛物线
定义及标准方程:
1.定义:
平面上到定点F和到定直线l距离相等的点的轨迹叫做抛物线,点F叫做抛物线的焦点,直线l叫做抛物线的准线
2.标准方程:
(1)(2)(3)(4)
【典例分析】
1.若动点P到点F(2,0)的距离与它到直线x+2=0的距离相等,则点P的轨迹方程为___________.
2.分别求满足下列条件的抛物线的标准方程。
(1)过点(3,-4)
(2)焦点在直线上;
(3)开口向下的抛物线上一点Q(m,-3)到焦点的距离等于5.
3.已知抛物线的准线与圆相切,则P的值为________。
4.已知抛物线的焦点是F,点P是抛物线上的动点,又有点A(3,2),求|PA|+|PF|的最小值,并求出取最小值时P点坐标。
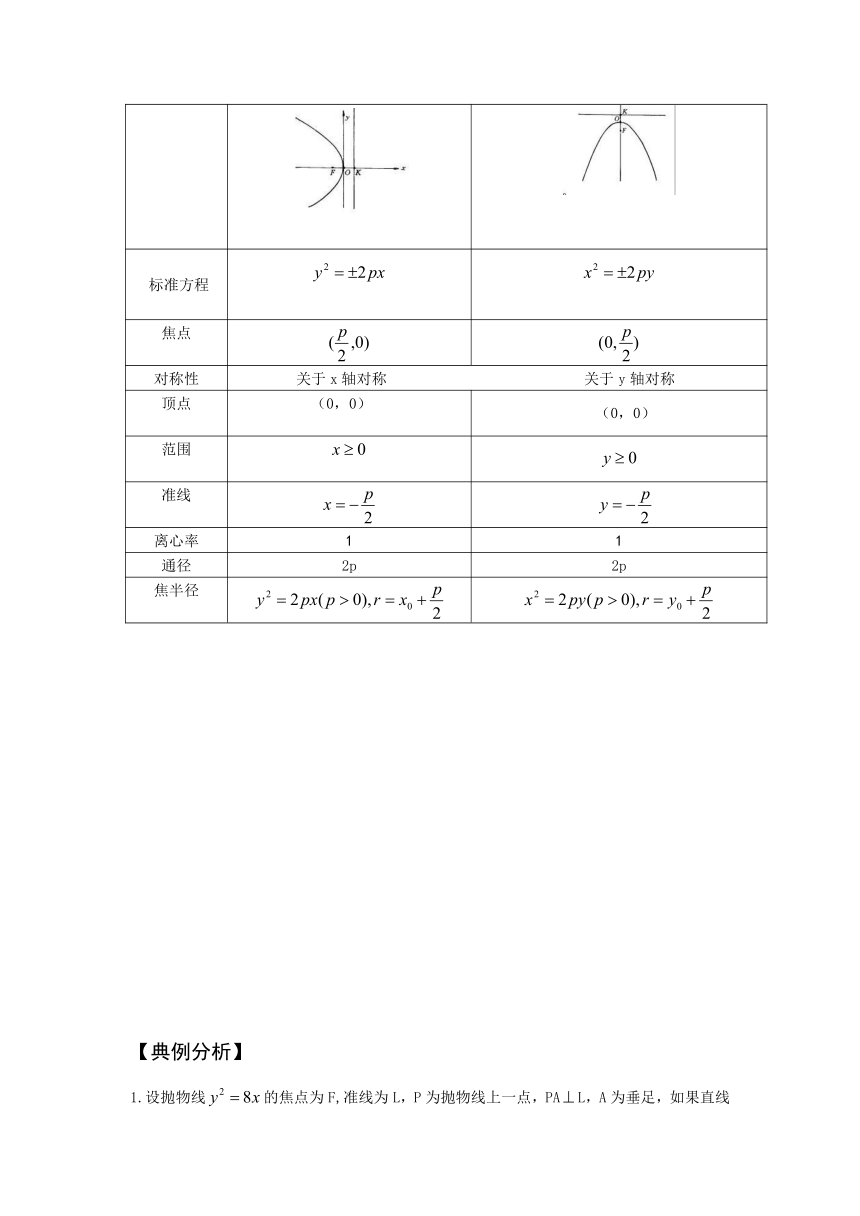
二.简单几何性质:
焦点在x轴上 焦点在y轴上
图形与方程
标准方程
焦点
对称性 关于x轴对称 关于y轴对称
顶点 (0,0) (0,0)
范围
准线
离心率 1 1
通径 2p 2p
焦半径
【典例分析】
设抛物线的焦点为F,准线为L,P为抛物线上一点,PAL,A为垂足,如果直线AF的斜率为,那么|PF|等于____________。
设抛物线的焦点为F,点A(0,2)若线段FA的中点B在抛物线上,则B到该抛物线准线的距离为_____________。
过抛物线的焦点F做倾斜角为的直线交抛物线与A,B两点,若线段AB的长为8,则p=______________。
已知点F为抛物线的焦点,O为原点,点p是抛物线准线上一动点,点A在抛物线上,且|AF|=4,则|PA|+|PO|的最小值为( )
A.6 B. C. D.4+2
抛物线的焦点为F,过点P(,1)的直线交抛物线与A,B点,且P恰为AB中点,则|AF|+|BF|=___________.
直线与抛物线的位置关系
直线与抛物线的位置关系:(1)相交
(2)相切
(3)相离
判断方法:代数法(联立直线方程与抛物线方程,求)
直线与抛物线交于A,B两点则有AB为抛物线的弦,设,弦中点。
(1)弦长
(2)
(3)直线AB的方程为
(4)直线AB的垂直平分线方程为
4.焦点弦:AB为抛物线过焦点的弦,设,弦中点。
(1)
(2)
(3)弦长,即当时,通径最短,为2p。
(4)弦长(为AB的倾斜角)
(5)
(6)以AB为直径的圆与准线相切
【典例分析】
已知抛物线上存在关于直线x+y=0对称的相异两点A,B,则|AB|等于_________。
设抛物线的焦点为F,过点M(,0)的直线与抛物线相交与A,B两点,与抛物线的准线相交与点C,|BF|=2,则的面积比等于( )
B. C. D.
已知以F为焦点的抛物线上的两点A,B满足,则弦AB的中点到准线的距离为________.
过抛物线(p>0)的焦点做斜率为1的直线与该抛物线交于A,B两点,A,B在x轴上的正射影分别为D,C。若梯形ABCD的面积为12,则p=____________。
已知抛物线C:的准线为l,过M(1,0),且斜率为的直线与l相交于点A,与C的一个交点为B,若,则p=__________。
已知抛物线C的顶点在坐标原点,焦点为F(1,0),直线l与抛物线C相交与A,B两点。若AB的中点为(2,2),则直线l的方程为____________。
已知抛物线C:的焦点F,过点K(-1,0)的直线l与C相交于A.B两点,点A关于x轴的对称点为D.(1)求证点F在直线BD上
(2)设,求的内切圆M的方程。
参考答案:
一.定义及标准方程
(1)(2)(3)
3.2
,(2,2)
二.几何性质
1.8
2.
3.2
4.C
5.7
直线与抛物线位置关系
1.
2.A
3.
4.2
5.2
6.y=x
7.
定义及标准方程:
1.定义:
平面上到定点F和到定直线l距离相等的点的轨迹叫做抛物线,点F叫做抛物线的焦点,直线l叫做抛物线的准线
2.标准方程:
(1)(2)(3)(4)
【典例分析】
1.若动点P到点F(2,0)的距离与它到直线x+2=0的距离相等,则点P的轨迹方程为___________.
2.分别求满足下列条件的抛物线的标准方程。
(1)过点(3,-4)
(2)焦点在直线上;
(3)开口向下的抛物线上一点Q(m,-3)到焦点的距离等于5.
3.已知抛物线的准线与圆相切,则P的值为________。
4.已知抛物线的焦点是F,点P是抛物线上的动点,又有点A(3,2),求|PA|+|PF|的最小值,并求出取最小值时P点坐标。
二.简单几何性质:
焦点在x轴上 焦点在y轴上
图形与方程
标准方程
焦点
对称性 关于x轴对称 关于y轴对称
顶点 (0,0) (0,0)
范围
准线
离心率 1 1
通径 2p 2p
焦半径
【典例分析】
设抛物线的焦点为F,准线为L,P为抛物线上一点,PAL,A为垂足,如果直线AF的斜率为,那么|PF|等于____________。
设抛物线的焦点为F,点A(0,2)若线段FA的中点B在抛物线上,则B到该抛物线准线的距离为_____________。
过抛物线的焦点F做倾斜角为的直线交抛物线与A,B两点,若线段AB的长为8,则p=______________。
已知点F为抛物线的焦点,O为原点,点p是抛物线准线上一动点,点A在抛物线上,且|AF|=4,则|PA|+|PO|的最小值为( )
A.6 B. C. D.4+2
抛物线的焦点为F,过点P(,1)的直线交抛物线与A,B点,且P恰为AB中点,则|AF|+|BF|=___________.
直线与抛物线的位置关系
直线与抛物线的位置关系:(1)相交
(2)相切
(3)相离
判断方法:代数法(联立直线方程与抛物线方程,求)
直线与抛物线交于A,B两点则有AB为抛物线的弦,设,弦中点。
(1)弦长
(2)
(3)直线AB的方程为
(4)直线AB的垂直平分线方程为
4.焦点弦:AB为抛物线过焦点的弦,设,弦中点。
(1)
(2)
(3)弦长,即当时,通径最短,为2p。
(4)弦长(为AB的倾斜角)
(5)
(6)以AB为直径的圆与准线相切
【典例分析】
已知抛物线上存在关于直线x+y=0对称的相异两点A,B,则|AB|等于_________。
设抛物线的焦点为F,过点M(,0)的直线与抛物线相交与A,B两点,与抛物线的准线相交与点C,|BF|=2,则的面积比等于( )
B. C. D.
已知以F为焦点的抛物线上的两点A,B满足,则弦AB的中点到准线的距离为________.
过抛物线(p>0)的焦点做斜率为1的直线与该抛物线交于A,B两点,A,B在x轴上的正射影分别为D,C。若梯形ABCD的面积为12,则p=____________。
已知抛物线C:的准线为l,过M(1,0),且斜率为的直线与l相交于点A,与C的一个交点为B,若,则p=__________。
已知抛物线C的顶点在坐标原点,焦点为F(1,0),直线l与抛物线C相交与A,B两点。若AB的中点为(2,2),则直线l的方程为____________。
已知抛物线C:的焦点F,过点K(-1,0)的直线l与C相交于A.B两点,点A关于x轴的对称点为D.(1)求证点F在直线BD上
(2)设,求的内切圆M的方程。
参考答案:
一.定义及标准方程
(1)(2)(3)
3.2
,(2,2)
二.几何性质
1.8
2.
3.2
4.C
5.7
直线与抛物线位置关系
1.
2.A
3.
4.2
5.2
6.y=x
7.
同课章节目录
