四川省宣汉县第二中学(新课标人教版)高三数学复习《平面向量》
文档属性
| 名称 | 四川省宣汉县第二中学(新课标人教版)高三数学复习《平面向量》 |  | |
| 格式 | zip | ||
| 文件大小 | 326.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-18 08:06:08 | ||
图片预览




文档简介
平面向量
一.向量概念
1.向量定义:既有大小又有方向的量叫做向量。
2.向量的表示方法:(1)用有向线段表示;
(2)用字母表示:
说明:(1)具有方向的线段叫有向线段。有向线段的三要素:起点、方向和长度;
(2)向量的长度(或称模):线段的长度叫向量的长度,记作.
3.单位向量、零向量、平行向量、相等向量、共线向量的定义:
(1)单位向量:长度为1的向量叫单位向量,即;
(2)零向量:长度为零的向量叫零向量,记作;
(3)平行向量:方向相同或相反的非零向量叫平行向量,记作:;
(4)相等向量:长度相等,方向相同的向量叫相等向量。即:;
(5)共线向量:平行向量都可移到同一直线上。平行向量也叫共线向量。
说明:(1)规定:零向量与任一向量平行,记作;
(2)零向量与零向量相等,记作;
(3)任意二个非零相等向量可用同一条有向线段表示,与有向线段的起点无关。
【典例分析】
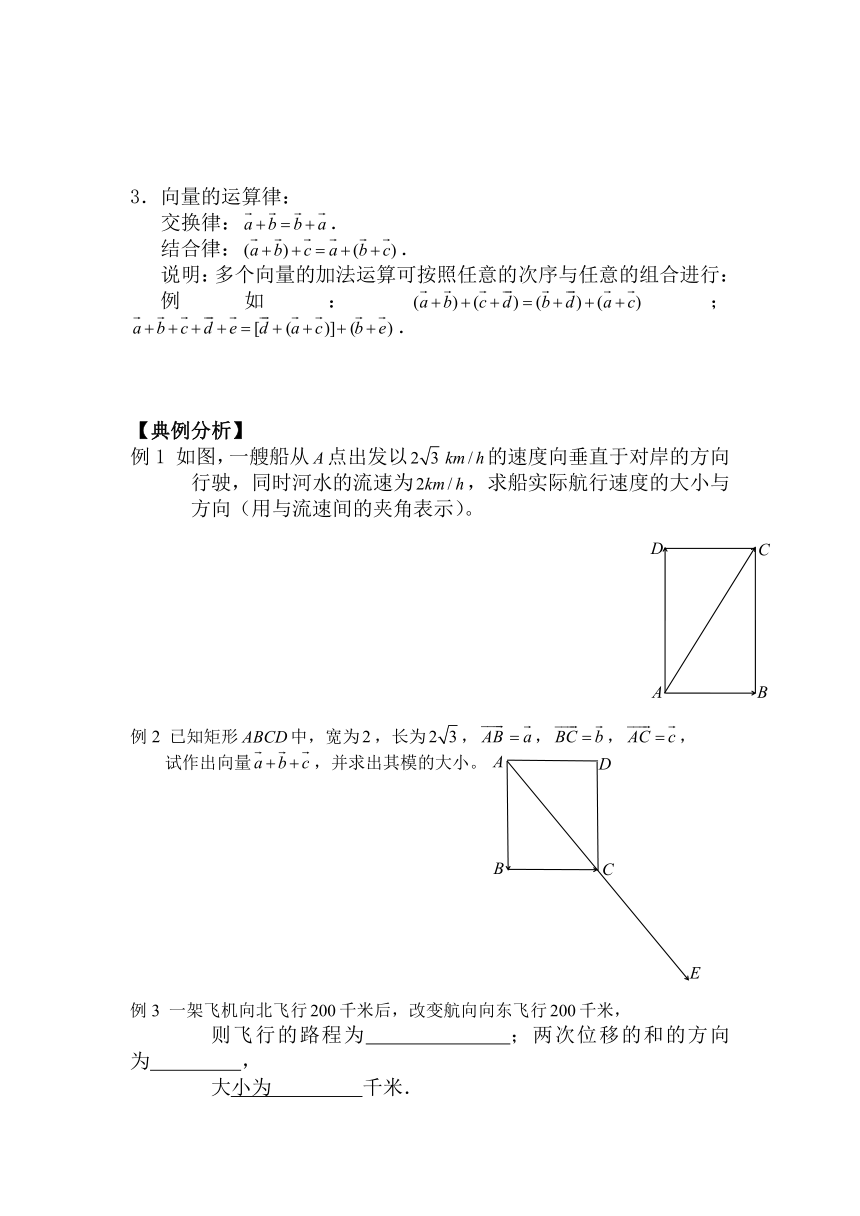
例1 如图1,设是正六边形的中心,分别
写出图中与向量,,相等的向量。
例2 如图2,梯形中,,分别是腰、
的三等分点,且,,求.
例3 在直角坐标系中,已知,与轴正方向所成的角为,与轴正方向所成的角为,试作出.
例4.已知点是正六边形的中心,则下列向量组中含有相等向量的是( )
()、、、 ()、、、
()、、、 ()、、、
二.向量的加法
1.向量的加法:求两个向量和的运算叫做向量的加法。表示:.
规定:零向量与任一向量,都有.
说明:①共线向量的加法:
②不共线向量的加法:如图(1),已知向量,,求作向量.
作法:在平面内任取一点(如图(2)),作,,则 .
(1) (2)
2.向量加法的法则:
(1)三角形法则:根据向量加法定义得到的求向量和的方法,称为向量加法的三角形法则。
表示:.
(2)平行四边形法则:以同一点为起点的两个已知向量,为邻边作,则以为起点的对角线就是与的和,这种求向量和的方法称为向量加法的平行四边形法则。
3.向量的运算律:
交换律:.
结合律:.
说明:多个向量的加法运算可按照任意的次序与任意的组合进行:
例如:;.
【典例分析】
例1 如图,一艘船从点出发以的速度向垂直于对岸的方向行驶,同时河水的流速为,求船实际航行速度的大小与方向(用与流速间的夹角表示)。
例2 已知矩形中,宽为,长为,,,,
试作出向量,并求出其模的大小。
例3 一架飞机向北飞行千米后,改变航向向东飞行千米,
则飞行的路程为 ;两次位移的和的方向为 ,
大小为 千米.
三.向量的减法
1.相反向量:与长度相等,方向相反的向量,叫做的相反向量,记作。
说明:(1)规定:零向量的相反向量是零向量。
(2)性质:;.
2.向量的减法:求两个向量差的运算,叫做向量的减法。表示.
3.向量减法的法则:
已知如图有,,求作.
(1)三角形法则:在平面内任取一点,作,,则.
说明:可以表示为从的终点指向的终点的向量(,有共同起点).
(2)平行四边形:在平面内任取一点,作 ,,
则.
思考:若,怎样作出?
四.向量的数乘
1.实数与向量的积的定义:
一般地,实数与向量的积是一个向量,记作,它的长度与方向规定如下:
(1);
(2)当时,的方向与的方向相同;
当时,的方向与的方向相反;
当 时,.
2.实数与向量的积的运算律:
(1)(结合律);
(2)(第一分配律);
(3)(第二分配律).
例1 计算:(1); (2); (3).
3.向量共线的充要条件:
定理:(向量共线的充要条件)向量与非零向量共线的充要条件是有且只有一个实数,使得.
例2 如图,已知,.试判断与是否共线.
例3 判断下列各题中的向量是否共线:
(1),;
(2),,且,共线.
例4 设是两个不共线的向量,已知,,, 若,,三点共线,求的值。
4.平面向量基本定理:
如果,是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数,,使.其中我们把不共线的向量,叫做表示这一平面所有向量的一组基底。
注:①,均非零向量;
②,不唯一(事先给定);
③,唯一;
④时,与共线;时,与共线;时,.
【典例分析】
例5 已知向量,(如图),求作向量.
例6如图 的两条对角线相交于点,且,,用、表示、、和.
例7 如图,、不共线,,用、表示.
例8已知在四边形中,,,,
求证:是梯形。
五.平面向量基本定理
1.向量的坐标表示的定义:
分别选取与轴、轴方向相同的单位向量,作为基底,对于任一向量,,(),实数对叫向量的坐标,记作.
其中叫向量在轴上的坐标,叫向量在轴上的坐标。
说明:(1)对于,有且仅有一对实数与之对应;
(2)相等的向量的坐标也相同;
(3),,;
(4)从原点引出的向量的坐标就是点的坐标。
例1 如图,用基底,分别表示向量、、、, 并求出它们的坐标。
2.平面向量的坐标运算:
问题:已知,,求,.
解:
即.
同理:.
结论:两个向量和与差的坐标分别等于这两个向量相应坐标的和与差。
3.向量的坐标计算公式:
归纳:(1)一个向量的坐标等于表示它的有向线段的终点坐标减去始点坐标;
(2)两个向量相等的充要条件是这二个向量的坐标相等。
4.实数与向量的积的坐标:
已知和实数,求
结论:实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标。
归纳:(1)设点,,则;
(2),,则,
,;
(3).向量与非零向量平行的充要条件是:.例2 已知,,求,,的坐标.
解:=;;
.
例2已知 ABCD的三个顶点的坐标分别为、、,求顶点的坐标。
例3已知,,,且,求,.
六.平面向量的坐标运算
1.向量平行的坐标表示:
设,,(),且,
则,∴.
∴,∴.
归纳:向量平行(共线)的充要条件的两种表达形式:
①;
②且设,()
【典例分析】
例1 已知,,且,求.
例2 已知,,,求证、、三点共线.
例3 已知,,若与平行,求.
例4已知点,,,,向量与平行吗?直线与直线平行吗?
七.向量的数量积
1.向量的夹角:
已知两个向量和(如图),作,,则
()叫做向量与的夹角。
当时,与同向;
当时,与反向;
当时,与的夹角是,我们说与垂直,记作.
2.向量数量积的定义:
已知两个非零向量和,它们的夹角为,则数量叫做与的数量积(或内积),记作,即.
说明:①两个向量的数量积是一个数量,这个数量的大小与两个向量的长度及其夹角
有关;
②实数与向量的积与向量数量积的本质区别:两个向量的数量积是一个数量;实
数与向量的积是一个向量;
③规定,零向量与任一向量的数量积是.
3.数量积的几何意义:
(1)投影的概念:
如图,,,过点作垂直于直线,垂足为,则.
叫做向量在方向上的投影,当为锐角时,它是正值;当为钝角时,它
是一负值;当时,它是;当时,它是;当时,它是.
的几何意义:数量积等于的长度与在的方向上的投影的乘积。
【典例分析】
例1 ①已知,,与的夹角,则 ;
②已知,在上的投影是,则 ;
③已知,,,则与的夹角
(3)数量积的性质:
设、都是非零向量,是与的夹角,则
①;
②当与同向时,;当与反向时,;
特别地:或;
③;
④;
若是与方向相同的单位向量,则
⑤.
【典例分析】
例2已知正的边长为,设,,,求.
例3已知,,,且,求.
4.向量数量积的坐标表示:设 ,则,
∴.
从而得向量数量积的坐标表示公式:.
5.长度、夹角、垂直的坐标表示:
①长度: ;
②两点间的距离公式:若,则;
③夹角:;
④垂直的充要条件:∵,即
(注意与向量共线的坐标表示的区别)
【典例分析】
例4 设,求.
例5已知,求证是直角三角形。
例6在中,,,求值。
答案
一、1、=== === ===
2、=3
4、D
二、1、4km/h、方向与流速的夹角为
2、8
3、400km、东偏北、200km
四、1、(1)-12 (2)5 (3)- +5-2
2、共线
3、(1)共线 (2)共线
4、-8
6、=-(+)/2 =(-)/2 =(+)/2 =(-)/2
7、=t(-)
8、证明:=++
=-8-2
=2(-4-)
=2 即
ABCD是梯形
五、1、=2+2=(2,2) =-2+2=(-2,2) =-2-2=(-2,-2)
=2-2=(2,-2)
2、D(2,2)
3、x=2,y=-3
六、1、3
2、证明:=(2,4) =(1,2) 即A、B、C三点共线
3、k=/5
4、平行、平行
七、1、-10 8 arccos-3/20
2、-8
3、-3-9/2
4、-2
6、k=-2/3或11/3或3/2
(图1)
(图2)
一.向量概念
1.向量定义:既有大小又有方向的量叫做向量。
2.向量的表示方法:(1)用有向线段表示;
(2)用字母表示:
说明:(1)具有方向的线段叫有向线段。有向线段的三要素:起点、方向和长度;
(2)向量的长度(或称模):线段的长度叫向量的长度,记作.
3.单位向量、零向量、平行向量、相等向量、共线向量的定义:
(1)单位向量:长度为1的向量叫单位向量,即;
(2)零向量:长度为零的向量叫零向量,记作;
(3)平行向量:方向相同或相反的非零向量叫平行向量,记作:;
(4)相等向量:长度相等,方向相同的向量叫相等向量。即:;
(5)共线向量:平行向量都可移到同一直线上。平行向量也叫共线向量。
说明:(1)规定:零向量与任一向量平行,记作;
(2)零向量与零向量相等,记作;
(3)任意二个非零相等向量可用同一条有向线段表示,与有向线段的起点无关。
【典例分析】
例1 如图1,设是正六边形的中心,分别
写出图中与向量,,相等的向量。
例2 如图2,梯形中,,分别是腰、
的三等分点,且,,求.
例3 在直角坐标系中,已知,与轴正方向所成的角为,与轴正方向所成的角为,试作出.
例4.已知点是正六边形的中心,则下列向量组中含有相等向量的是( )
()、、、 ()、、、
()、、、 ()、、、
二.向量的加法
1.向量的加法:求两个向量和的运算叫做向量的加法。表示:.
规定:零向量与任一向量,都有.
说明:①共线向量的加法:
②不共线向量的加法:如图(1),已知向量,,求作向量.
作法:在平面内任取一点(如图(2)),作,,则 .
(1) (2)
2.向量加法的法则:
(1)三角形法则:根据向量加法定义得到的求向量和的方法,称为向量加法的三角形法则。
表示:.
(2)平行四边形法则:以同一点为起点的两个已知向量,为邻边作,则以为起点的对角线就是与的和,这种求向量和的方法称为向量加法的平行四边形法则。
3.向量的运算律:
交换律:.
结合律:.
说明:多个向量的加法运算可按照任意的次序与任意的组合进行:
例如:;.
【典例分析】
例1 如图,一艘船从点出发以的速度向垂直于对岸的方向行驶,同时河水的流速为,求船实际航行速度的大小与方向(用与流速间的夹角表示)。
例2 已知矩形中,宽为,长为,,,,
试作出向量,并求出其模的大小。
例3 一架飞机向北飞行千米后,改变航向向东飞行千米,
则飞行的路程为 ;两次位移的和的方向为 ,
大小为 千米.
三.向量的减法
1.相反向量:与长度相等,方向相反的向量,叫做的相反向量,记作。
说明:(1)规定:零向量的相反向量是零向量。
(2)性质:;.
2.向量的减法:求两个向量差的运算,叫做向量的减法。表示.
3.向量减法的法则:
已知如图有,,求作.
(1)三角形法则:在平面内任取一点,作,,则.
说明:可以表示为从的终点指向的终点的向量(,有共同起点).
(2)平行四边形:在平面内任取一点,作 ,,
则.
思考:若,怎样作出?
四.向量的数乘
1.实数与向量的积的定义:
一般地,实数与向量的积是一个向量,记作,它的长度与方向规定如下:
(1);
(2)当时,的方向与的方向相同;
当时,的方向与的方向相反;
当 时,.
2.实数与向量的积的运算律:
(1)(结合律);
(2)(第一分配律);
(3)(第二分配律).
例1 计算:(1); (2); (3).
3.向量共线的充要条件:
定理:(向量共线的充要条件)向量与非零向量共线的充要条件是有且只有一个实数,使得.
例2 如图,已知,.试判断与是否共线.
例3 判断下列各题中的向量是否共线:
(1),;
(2),,且,共线.
例4 设是两个不共线的向量,已知,,, 若,,三点共线,求的值。
4.平面向量基本定理:
如果,是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数,,使.其中我们把不共线的向量,叫做表示这一平面所有向量的一组基底。
注:①,均非零向量;
②,不唯一(事先给定);
③,唯一;
④时,与共线;时,与共线;时,.
【典例分析】
例5 已知向量,(如图),求作向量.
例6如图 的两条对角线相交于点,且,,用、表示、、和.
例7 如图,、不共线,,用、表示.
例8已知在四边形中,,,,
求证:是梯形。
五.平面向量基本定理
1.向量的坐标表示的定义:
分别选取与轴、轴方向相同的单位向量,作为基底,对于任一向量,,(),实数对叫向量的坐标,记作.
其中叫向量在轴上的坐标,叫向量在轴上的坐标。
说明:(1)对于,有且仅有一对实数与之对应;
(2)相等的向量的坐标也相同;
(3),,;
(4)从原点引出的向量的坐标就是点的坐标。
例1 如图,用基底,分别表示向量、、、, 并求出它们的坐标。
2.平面向量的坐标运算:
问题:已知,,求,.
解:
即.
同理:.
结论:两个向量和与差的坐标分别等于这两个向量相应坐标的和与差。
3.向量的坐标计算公式:
归纳:(1)一个向量的坐标等于表示它的有向线段的终点坐标减去始点坐标;
(2)两个向量相等的充要条件是这二个向量的坐标相等。
4.实数与向量的积的坐标:
已知和实数,求
结论:实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标。
归纳:(1)设点,,则;
(2),,则,
,;
(3).向量与非零向量平行的充要条件是:.例2 已知,,求,,的坐标.
解:=;;
.
例2已知 ABCD的三个顶点的坐标分别为、、,求顶点的坐标。
例3已知,,,且,求,.
六.平面向量的坐标运算
1.向量平行的坐标表示:
设,,(),且,
则,∴.
∴,∴.
归纳:向量平行(共线)的充要条件的两种表达形式:
①;
②且设,()
【典例分析】
例1 已知,,且,求.
例2 已知,,,求证、、三点共线.
例3 已知,,若与平行,求.
例4已知点,,,,向量与平行吗?直线与直线平行吗?
七.向量的数量积
1.向量的夹角:
已知两个向量和(如图),作,,则
()叫做向量与的夹角。
当时,与同向;
当时,与反向;
当时,与的夹角是,我们说与垂直,记作.
2.向量数量积的定义:
已知两个非零向量和,它们的夹角为,则数量叫做与的数量积(或内积),记作,即.
说明:①两个向量的数量积是一个数量,这个数量的大小与两个向量的长度及其夹角
有关;
②实数与向量的积与向量数量积的本质区别:两个向量的数量积是一个数量;实
数与向量的积是一个向量;
③规定,零向量与任一向量的数量积是.
3.数量积的几何意义:
(1)投影的概念:
如图,,,过点作垂直于直线,垂足为,则.
叫做向量在方向上的投影,当为锐角时,它是正值;当为钝角时,它
是一负值;当时,它是;当时,它是;当时,它是.
的几何意义:数量积等于的长度与在的方向上的投影的乘积。
【典例分析】
例1 ①已知,,与的夹角,则 ;
②已知,在上的投影是,则 ;
③已知,,,则与的夹角
(3)数量积的性质:
设、都是非零向量,是与的夹角,则
①;
②当与同向时,;当与反向时,;
特别地:或;
③;
④;
若是与方向相同的单位向量,则
⑤.
【典例分析】
例2已知正的边长为,设,,,求.
例3已知,,,且,求.
4.向量数量积的坐标表示:设 ,则,
∴.
从而得向量数量积的坐标表示公式:.
5.长度、夹角、垂直的坐标表示:
①长度: ;
②两点间的距离公式:若,则;
③夹角:;
④垂直的充要条件:∵,即
(注意与向量共线的坐标表示的区别)
【典例分析】
例4 设,求.
例5已知,求证是直角三角形。
例6在中,,,求值。
答案
一、1、=== === ===
2、=3
4、D
二、1、4km/h、方向与流速的夹角为
2、8
3、400km、东偏北、200km
四、1、(1)-12 (2)5 (3)- +5-2
2、共线
3、(1)共线 (2)共线
4、-8
6、=-(+)/2 =(-)/2 =(+)/2 =(-)/2
7、=t(-)
8、证明:=++
=-8-2
=2(-4-)
=2 即
ABCD是梯形
五、1、=2+2=(2,2) =-2+2=(-2,2) =-2-2=(-2,-2)
=2-2=(2,-2)
2、D(2,2)
3、x=2,y=-3
六、1、3
2、证明:=(2,4) =(1,2) 即A、B、C三点共线
3、k=/5
4、平行、平行
七、1、-10 8 arccos-3/20
2、-8
3、-3-9/2
4、-2
6、k=-2/3或11/3或3/2
(图1)
(图2)
同课章节目录
