2023届高考二轮总复习课件(适用于老高考旧教材) 数学(文)专题四 概率与统计(共122张PPT)
文档属性
| 名称 | 2023届高考二轮总复习课件(适用于老高考旧教材) 数学(文)专题四 概率与统计(共122张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 17:31:03 | ||
图片预览










文档简介
(共122张PPT)
专题四 概率与统计
上篇
内容索引
01
02
03
高考小题突破6 概率与统计的基本运算
培优拓展 巧比较解决统计图表创新题中的数据分析
◎高考保分大题四 概率与统计的综合问题
04
培优拓展 巧转化速解非线性回归问题
考情分析 1.题型、题量稳定:近年来,高考对该部分的考查一般为“2小1大”,分值约22分,多为中、低档题.
2.重点突出:(1)客观题重点考查抽样方法、用样本估计总体、古典概型、几何概型、样本、数据的数字特征等,难度较低;(2)主观题以现实生活中的真实情境为背景,考察回归分析、独立性检验以及统计与概率的综合应用等,常与实际生活中的统计图表相结合,阅读量大,多为中等难度.
3.核心素养:逻辑推理、数学运算.
备考策略 1.把握关键:数据的统计与分析是统计与概率的核心,也是高考命题的重点与热点,灵活利用数据的数字特征、辨清事件的性质与类型是解决该部分问题的关键.
2.加强计算:该部分考题无论是数据的分析还是概率的求解,准确地进行运算是基础,所以要加强基本的数据处理、运算能力.
3.加强阅读能力:概率与统计问题多与社会、生活、科技等情境问题相结合,从情境中读取有用信息,并建立正确的数学模型是解决该部分问题的关键环节.
真题感悟
1.(2022·全国甲·文6)从分别写有1,2,3,4,5,6的6张卡片中无放回随机抽取2张,则抽到的2张卡片上的数字之积是4的倍数的概率为( )
答案 C
解析 从6张卡片中无放回随机抽取2张,所有可能的结果是(1,2),(1,3),
(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共15种,其中数字之积是4的倍数的结果是(1,4),(2,4),(2,6),(3,4),(4,5),(4,6)共6
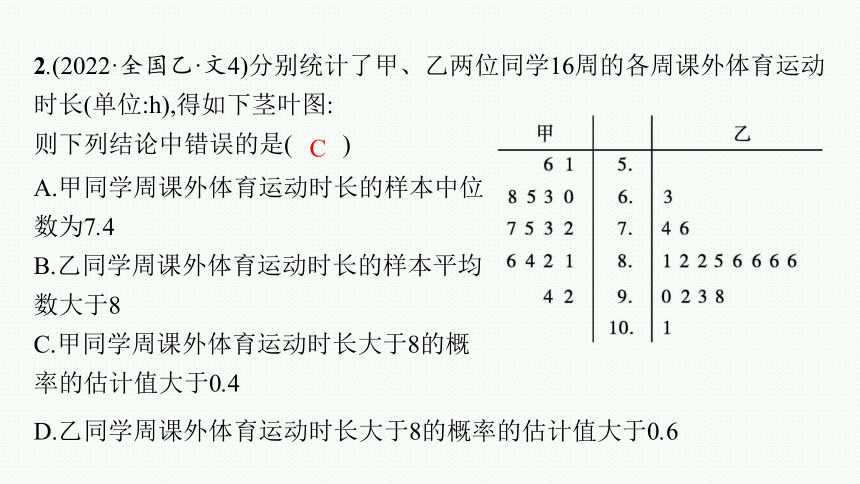
2.(2022·全国乙·文4)分别统计了甲、乙两位同学16周的各周课外体育运动时长(单位:h),得如下茎叶图:
则下列结论中错误的是( )
A.甲同学周课外体育运动时长的样本中位数为7.4
B.乙同学周课外体育运动时长的样本平均数大于8
C.甲同学周课外体育运动时长大于8的概率的估计值大于0.4
D.乙同学周课外体育运动时长大于8的概率的估计值大于0.6
C
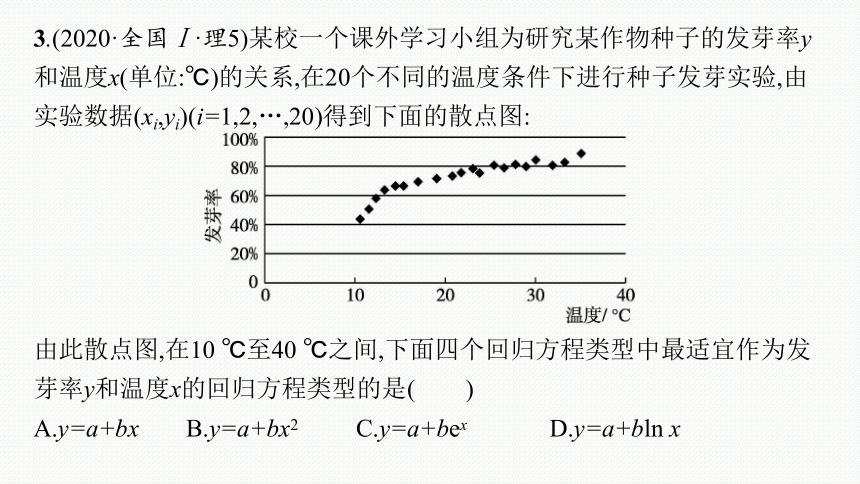
3.(2020·全国Ⅰ·理5)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(xi,yi)(i=1,2,…,20)得到下面的散点图:
由此散点图,在10 ℃至40 ℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
A.y=a+bx B.y=a+bx2 C.y=a+bex D.y=a+bln x
答案 D
解析 结合题中散点图,由图象的大致走向判断,此函数应该是对数函数模型,故应该选用的函数模型为y=a+bln x.
4.(2019·全国Ⅱ·文14)我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为 .
答案 0.98
解析 由题意,得经停该高铁站的列车的正点数约为10×0.97+20×0.98+10×0.99=39.2,其中车次数为10+20+10=40,所以经停该站高铁列车所有车次的平均正点率的估计值为 =0.98.
5.(2022·全国甲·文17)甲、乙两城之间的长途客车均由A和B两家公司运营,为了解这两家公司长途客车的运行情况,随机调查了甲、乙两城之间的500个班次,得到下面列联表:
公司 准点班次数 未准点班次数
A 240 20
B 210 30
(1)根据上表,分别估计这两家公司甲、乙两城之间的长途客车准点的概率;
(2)能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关
P(K2≥k0) 0.100 0.050 0.010
k0 2.706 3.841 6.635
解 (1)A公司一共调查了260个班次的长途客车,其中有240个班次的长途客车准点,故A公司的长途客车准点的概率为 ≈0.923,B公司一共调查了240个班次的长途客车,其中有210个班次的长途客车准点,故B公司的长途客车准点的概率为 =0.875.
(2)根据已知数据得到列联表如下:
公司 准点班次数 未准点班次数 合计
A 240 20 260
B 210 30 240
合计 450 50 500
所以有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关.
知识精要
1.样本数据x1,x2,…,xn的数字特征
2.频率分布直方图
(1)小长方形的面积等于频率,各小长方形的面积的总和等于1.
(2)最高的小长方形底边中点的横坐标即是众数.
(3)中位数左边和右边的小长方形的面积和是相等的.
(4)平均数等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和(同一组中的数据用该组区间的中点值为代表).
误区警示
(1)频率分布直方图中纵轴表示的是 ,不是频率.
(2)每组的频率等于该组小长方形的面积,不是该组小长方形的高.
3.变量间的相关关系
(1)如果散点图中的点从整体上看大致分布在一条直线的附近,那么我们说变量x和y具有线性相关关系.
(2)线性回归方程:若变量x与y具有线性相关关系,有n个样本数据
当r>0时,表示两个变量正相关;当r<0时,表示两个变量负相关.|r|越接近1,表明两个变量相关性越强;当|r|接近0时,表明两个变量几乎不存在相关性.
名师点析
4.独立性检验
对于取值分别是{x1,x2}和{y1,y2}的分类变量X和Y,其样本频数列联表是:
X Y 总计
y1 y2
x1 a b a+b
x2 c d c+d
总计 a+c b+d n
名师点析
K2的观测值k越大,说明“两个分类变量有关系”的可能性越大.
5.概率的基本性质及常见概率的计算
(1)随机事件的概率:0(2)若事件A,B互斥,则P(A∪B)=P(A)+P(B).
(3)若事件A,B对立,则P(A∪B)=P(A)+P(B)=1.
(4)古典概型的特点:有限性,等可能性;
需要重视的关键点
名师点析
常用排列、组合知识计算基本事件个数.
(7)相互独立事件同时发生的概率:P(AB)=P(A)P(B).
特别提醒
计算概率时,先判断概率类型,再代入对应公式计算.
(6)概率的估计值:当试验次数足够多时,常用频率估计概率.
高考小题突破6
考点一
统计图表及其应用
典例突破1(2021·全国甲·文2)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
答案 C
解析 该地农户家庭年收入低于4.5万元的农户比率估计为(0.02+0.04)×1=6%,A正确;
该地农户家庭年收入不低于10.5万元的农户比率估计为(0.04+0.02+0.02+0.02)×1=10%,B正确;
该地农户家庭年收入的平均值为0.02×3+0.04×4+0.1×5+0.14×6+0.2×7+0.2×8+0.1×9+0.1×10+0.04×11+0.02×12+0.02×13+0.02×14=7.68,C不正确;
该地农户家庭年收入介于4.5万元至8.5万元之间的比率为(0.1+0.14+0.2+0.2)×1=64%,D正确.
规律方法
统计图表的使用
(1)数据读取:读取数据时要结合问题背景理解图表意义,特别是频率分布直方图中的纵坐标,应为频率与组距的商.
(2)数据分析:数据的分析应遵循“用样本估计总体”的思想,抓住数据的数字特征.
对点练1(2022·陕西二模)小张一星期的总开支分布如图1所示,一星期的食品开支如图2所示,则小张一星期的肉类开支占总开支的百分比约为( )
图1
图2
A.10% B.8% C.5% D.4%
答案 A
解析 由题图知,小张一星期的食品开支为30+40+100+80+50=300(元),其中肉类开支为100元,占食品开支的 ,而食品开支占总开支的30%,所以小张一星期的肉类开支占总开支的百分比为30%× =10%.故选A.
考点二
回归分析与独立性检验
典例突破2(1)在一项调查中有两个变量x和y,下图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为y关于x的回归方程的函数类型是( )
A.y=a+bx B.y=p+qcx(q>0)
C.y=m+nx2(n>0) D.y=c+d
(2)(2022·重庆三模)北京2022年冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”一亮相,好评不断.为了研究“冰墩墩”与“雪容融”在不同性别的人群中受欢迎程度是否存在差异,某机构随机调查了100人,得到如下2×2列联表:
性别 男 女 总计
更喜欢“冰墩墩” 25 15 40
更喜欢“雪容融” 25 35 60
总计 50 50 100
P(K2≥k0) 0.100 0.050 0.010 0.001
k0 2.706 3.841 6.635 10.828
则下列说法正确的是( )
A.有95%以上的把握认为“对两个吉祥物的喜好倾向与性别无关”
B.有95%以上的把握认为“对两个吉祥物的喜好倾向与性别有关”
C.在犯错误的概率不超过1%的前提下,可以认为“对两个吉祥物的喜好倾向与性别无关”
D.在犯错误的概率不超过1%的前提下,可以认为“对两个吉祥物的喜好倾向与性别有关”
答案 (1)D (2)B
解析 (1)散点图呈曲线,A中函数为线性函数,不合题意,故排除A;由散点图可知整体呈增长态势,且增长速度变慢.对于B,函数为指数型函数,当c>1时函数单调递增,且增长速度变快,不合题意,当00时,函数为单调递增函数,且增长速度变慢,符合题意,故D正确.故选D.
(2)由列联表中的数据,可得k= ≈4.167>3.841,所以有95%以上的把握认为“对两个吉祥物的喜好倾向与性别有关”.故选B.
规律方法
1.非线性回归方程的求法
(1)根据原始数据作出散点图;
(2)根据散点图,选择恰当的拟合函数;
(3)做恰当变换,将其转化成线性函数,求线性回归方程;
(4)在(3)的基础上通过相应变换,即可得到非线性回归方程.
提醒:可以建立多个函数模型时,要对每个模型进行分析比较,选择最优模型.
2.独立性检验问题的解题步骤
(1)做出2×2列联表;
(2)计算随机变量K2的观测值k;
(3)查临界值,检验作答.
对点练2(1)(2022·辽宁葫芦岛二模)某生物兴趣小组为研究一种红铃虫的产卵数y与温度x(单位:℃)的关系,现收集了7组观测数据(xi,yi)(i=1,2,…,7)得到下面的散点图:
由此散点图,在20 ℃至36 ℃之间,下面四个回归方程类型中最适宜作为红铃虫产卵数y和温度x的回归方程类型的是( )
A.y=a+bx
C.y=a+bex
D.y=a+bln x
(2)(2022·四川成都三模)在某大学一食品超市,随机询问了70名大学生在购买食物时是否查看营养说明,得到如下的列联表:
性别 女 男 总计
要查看营养说明 15 25 40
不查看营养说明 20 10 30
总计 35 35 70
P(K2≥k0) 0.10 0.05 0.025 0.010
k0 2.706 3.841 5.024 6.635
则下列说法正确的是( )
A.在犯错误的概率不超过0.05的前提下认为该校大学生在购买食物时要查看营养说明的人数中男生人数更多
B.在犯错误的概率不超过0.010的前提下认为该校女大学生在购买食物时要查看营养说明的人数与不查看营养说明的人数比为
C.在犯错误的概率不超过0.025的前提下认为性别与是否查看营养说明有关系
D.在犯错误的概率不超过0.010的前提下认为性别与是否查看营养说明有关系
答案 (1)C (2)C
解析 (1)由散点图可以看出此函数是增函数,且增长速度越来越快,所以y=a+bex最适宜作为红铃虫产卵数y和温度x的回归方程类型.故选C.
(2)由列联表可得k= ≈5.833>5.024,所以在犯错误的概率不超过0.025的前提下认为性别与是否查看营养说明有关系.故选C.
考点三
古典概型
典例突破3(1)(2021·全国甲·文10)将3个1和2个0随机排成一行,则2个0不相邻的概率为( )
A.0.3 B.0.5 C.0.6 D.0.8
(2)(2022·全国乙·文14)从甲、乙等5名同学中随机选3名参加社区服务工作,则甲、乙都入选的概率为 .
解析 (1)将3个1和2个0随机排成一行,共有11100,00111,01110,11010,11001,
10110,10011,10101,01101,01011,10种排法,2个0不相邻的排法共有01110,11010,10110,10101,01101,01011,6种排法,故所求的概率为
(2)设除甲、乙外,其余三名同学为A,B,C.
从甲、乙等5名同学中随机选3名,则所有的可能结果为(甲,乙,A),(甲,乙,B),
(甲,乙,C),(甲,A,B),(甲,B,C),(甲,A,C),(乙,A,B),(乙,B,C),(乙,A,C),(A,B,C),共10个.甲、乙都入选的可能结果为(甲,乙,A),(甲,乙,B),(甲,乙,C),有3个.由古典概型公式计算,得甲、乙都入选的概率为 .
规律方法
求解古典概型的关键点
计数方法 常用到列举法、列表法、树状图等方法.
注意:1.判断事件是否与顺序相关;2.列举基本事件时,要按照一定的顺序,避免重复或遗漏
求解策略 较为复杂的计数问题,可以分解为互斥事件概率求解;也可以转化为对立事件的概率求解
对点练3(2020·全国Ⅰ·文4)设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为( )
(2)(2022·江西南昌二模)从装有3个红球和2个蓝球(除颜色外完全相同)的盒子中任取两个球,则选到的两个球颜色相同的概率为 .
解析 (1)由题意知一共有10种取法,当选A,O,C和B,O,D时符合要求,故
(2)3个红球记为a,b,c,2个蓝球记为A,B,则任取两个球有ab,ac,aA,aB,bc,bA,
bB,cA,cB,AB,共10种选法.其中颜色相同的有ab,ac,bc,AB,共4种选法.所以选
考点四
几何概型
(2)(2022·江西宜春模拟预测)如图所示,将4个全等的直角三角形拼成边长为a+b的正方形ABCD,使中间留下一个正方形EFGH.已知a=3,b=4,在正方形ABCD内随机取一点,则该点恰好取自阴影部分的概率为( )
答案 (1)B (2)B
规律方法
求解几何概型的基本步骤
(1)定型:即根据事件的性质确定概率概型;
(2)定性:准确判断几何概型中事件的度量方式,一般用长度、角度、面积或者体积表示;
(3)求量:即求解事件的度量,代入几何概型的求解公式求解.
对点练4(1)(2022·河南鲁山一中模拟)中国古代数学名著《九章算术》中记载:“圆周与其直径之比被定为3,圆中弓形面积为 a(a+c)(c为弦长,a为半径长与圆心到弦的距离之差).”据此计算,已知一个圆中弓形所对应的弦长c=6,a=1,质点M随机投入此圆中,则质点M落在该弓形内的概率为( )
(2)对称性是数学美的重要特征,是数学家追求的目标,也是数学发现与创造中的重要的美学因素.现用随机模拟的方法来估算对称蝴蝶(如图中阴影区域所示)的面积,做一个边长为2 dm的正方形将其包含在内,并向该正方形内随机投掷1 000个点,已知恰有395个点落在阴影区域内,据此可估计图中对称蝴蝶的面积是 dm2.
答案 (1)B (2)1.58
培优拓展
问题提出
统计图表有频率分布直方图、茎叶图、折线图、条形图、饼形图、雷达图等,它们广泛应用于实际生活中,也是历年高考的热点,求解此类问题的关键是由图表读出有用的数据,再根据数据进行分析.
数据的对比分析要抓住其数字特征,主要有以下三个角度的分析:
(1)平均数:反应这组数字的平均取值水平;
(2)方差:反应这组数字取值的离散程度,方差越大,说明取值越分散.
(3)变化趋势:主要涉及数据的增大或减小、数据变化的幅度大小等.
结论应用
类型一频率分布直方图
【例1】 某地计划引进一批果树树苗提供给果农种植.为了解果树树苗的生长情况,现从甲、乙两个品种中各随机抽取了100株,进行高度测量,并将高度数据制作成了如图所示的频率分布直方图.由频率分布直方图求得甲、乙两个品种高度的平均值都是66.5,用样本估计总体,则下列描述正确的是( )
A.甲品种的平均高度高于乙品种,且乙品种比甲品种长得整齐
B.乙品种的平均高度高于甲品种,且甲品种比乙品种长得整齐
C.甲、乙品种的平均高度差不多,且甲品种比乙品种长得整齐
D.甲、乙品种的平均高度差不多,且乙品种比甲品种长得整齐
甲品种
乙品种
答案 D
解析 由题知,甲、乙两个品种高度的平均值均为66.5,即甲、乙品种的平均高度差不多,从频率分布直方图可以看出乙品种比甲品种高度更集中,长得整齐.故选D.
类型二折线图
【例2】 如图所示为2021年3月到2022年3月某地居民消费价格的涨跌幅情况.
居民消费价格涨跌幅
关于这个时间段的折线图,有下列说法:
①所有月份的同比增长率都是正数;
②环比增长率为正数的月份比为负数的月份多;
③2021年9月到10月的同比增长率的增幅等于10月到11月的同比增长率的增幅;
④同比增长率的极差为0.9.
其中正确说法的个数为( )
A.1 B.2 C.3 D.4
答案 C
解析 ①显然是正确的;
②环比增长率为正数的有6个月,为负数的有5个月,故②正确;③2021年9月到10月的同比增长率的增幅为1.5-0.7=0.8,10月到11月的同比增长率的增幅为2.3-1.5=0.8,所以③的说法是正确的;④同比增长率的极差为2.3-0.4=1.9,所以④的说法是错误的.故选C.
类型三扇形图
【例3】 某商场开通三种平台销售商品,五一期间这三种平台的数据如图1所示.该商场为了解消费者对各平台销售方式的满意程度,用分层抽样的方法抽取了6%的顾客进行满意度调查,得到的数据如图2所示.下列说法正确的是( )
图1
图2
A.样本中对平台一满意的消费者人数约为700
B.估计总体中对平台二满意的消费者人数为18
C.样本中对平台一和平台二满意的消费者总人数约为60
D.若样本中对平台三满意的消费者人数为120,则m=90%
答案 C
解析 对于A,样本中对平台一满意的人数约为2 000×6%×35%=42,故选项A错误;对于B,总体中对平台二满意的人数约为1 500×20%=300,故选项B错误;对于C,样本中对平台一和平台二满意的总人数约为
2 000×6%×35%+1 500×6%×20%=60,故选项C正确;对于D,对平台三的满意率为 =80%,所以m=80%,故选项D错误.故选C.
类型四其他图表
【例4】 某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15 ℃,B点表示四月的平均最低气温约为5 ℃.下面叙述正确的个数为( )
①七月的平均温差比一月的平均温差大;②十月的平均温差最大;③三月和十一月的平均最高气温基本相同;④平均最高气温在15 ℃到20 ℃之间的月份至少有4个.
A.1 B.2 C.3 D.4
答案 B
解析 对于①,七月的平均最高气温点与平均最低气温点间的距离大于一月的平均最高气温点与平均最低气温点间的距离,所以七月的平均温差比一月的平均温差大,故①正确;对于②,十月的平均温差明显小于七月,故②不正确;对于③,三月和十一月的平均最高气温均为10 ℃,故③正确;对于④,平均最高气温在15 ℃到20 ℃之间的月份有五月、九月,共2个月份,故④不正确.故选B.
高考保分大题四
考点一
回归分析及应用
典例突破1(2022·河南焦作二模)小李准备在某商场租一间商铺开服装店,为了解市场行情,在该商场调查了20家服装店,统计得到了它们的面积x(单位:m2)和日均客流量y(单位:百人)的数据(xi,yi)(i=1,2,…,20),并计算
(1)求y关于x的回归直线方程;
(2)已知服装店每天的经济效益W=k +mx(k>0,m>0),该商场现有60~150 m2的商铺出租,根据(1)的结果进行预测,要使单位面积的经济效益Z最高,小李应该租多大面积的商铺
附:回归直线y=bx+a的斜率和截距的最小二乘估计分别为:
则f(x)=g(t)=0.15t-7.5t2=-7.5×(t-0.01)2+0.000 75,
当t=0.01,即x=100时,f(x)取最大值,
又因为k>0,m>0,所以此时Z也取最大值,
因此,小李应该租100 m2的商铺.
规律方法
线性回归分析问题的类型及解题方法
1.求回归直线方程:
2.对变量值预测:
(1)若已知回归直线方程(方程中无参数),进而预测时,可以直接将数值代入求得特定要求下的预测值;
(2)若回归直线方程中有参数,则根据回归直线一定经过点( ),求出参数值,得到回归直线方程,进而完成预测.
对点练1(2022·安徽合肥二模)据统计,截止到2020年底,我国私人汽车拥有量超过24千万辆.下图是2011年至2020年十年间我国私人汽车拥有量y(单位:千万辆)的折线图.
(注:年份代码1~10分别对应年份2011~2020)
(1)由折线图能够看出,可以用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(2)建立y关于t的线性回归方程(系数精确到0.01),并预测2023年我国私人汽车拥有量.
相关系数r≈0.998 8,说明y与t的线性相关性很高,
所以可以用线性回归模型拟合y与t的关系.
据此可以预测,2023年我国私人汽车拥有量将达到30.05千万辆.
考点二
独立性检验及其应用
典例突破2(2021·全国甲·文17)甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:
机床 产品质量 合计
一级品 二级品
甲机床 150 50 200
乙机床 120 80 200
合计 270 130 400
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少
(2)能否在犯错误的概率不超过0.01的情况下认为甲机床的产品质量与乙机床的产品质量有差异
P(K2≥k0) 0.050 0.010 0.001
k0 3.841 6.635 10.828
所以在犯错误的概率不超过0.01的情况下认为甲机床的产品质量与乙机床的产品质量有差异.
解题技巧
独立性检验的关键
(1)根据2×2列联表准确计算K2的观测值k,若2×2列联表没有列出来,要先列出此表;
(2)K2的观测值k越大,对应假设事件H0成立(两类变量相互独立)的概率越小,H0不成立的概率越大.
对点练2(2022·云南二模)某地举行演讲比赛,有60名选手参加了比赛,评委从演讲内容、演讲能力、演讲效果、综合印象四个分项为选手打分,各项成绩均按百分制计,然后再按演讲内容占40%,演讲能力占40%,演讲效果占15%,综合印象占5%,计算选手的比赛总成绩(百分制).
甲、乙两名选手的单项成绩如下表:
选手 演讲内容 演讲能力 演讲效果 综合印象
甲 85 90 85 90
乙 87 88 90 87
(1)分别计算甲、乙两名选手的比赛总成绩;
(2)比赛结束后,对参赛的60名选手的性别和获奖情况进行统计,情况如下表:
性别 获奖 未获奖
男 10 15
女 15 20
能否有90%的把握认为这次演讲比赛,选手获奖与选手性别有关
P(K2≥k0) 0.15 0.10 0.010 0.001
k0 2.072 2.706 6.635 10.828
解 (1)甲选手的比赛总成绩:85×40%+90×40%+85×15%+90×5%=87.25(分).
乙选手的比赛总成绩:87×40%+88×40%+90×15%+87×5%=87.85(分).
∴没有90%的把握认为选手获奖与选手性别有关.
考点三
统计图表与概率的综合
典例突破3(2022·江西萍乡二模)第24届冬奥会于2022年2月4日至2月20日在北京举行,组委会为普及冬奥知识,面向全市征召a名志愿者成立冬奥知识宣传小组,现把该小组成员按年龄分成[20,25),[25,30),[30,35),[35,40),
[40,45]这5组,得到的频率分布直方图如图所示,已知年龄在[25,30)内的人数为35.
(1)求m和a的值,并估计该冬奥知识宣传小组成员年龄的中位数(精确到0.1);
(2)若用分层抽样的方法从年龄在[30,35),[35,40),[40,45]内的志愿者中抽取6名参加某社区的宣传活动,再从这6名志愿者中随机抽取2名去该社区的一所高中组织一次冬奥知识宣讲,求这2名志愿者中至少有1人年龄在[35,40)内的概率.
解 (1)由频率分布直方图知,(0.01+m+0.06+0.04+0.02)×5=1,解得m=0.07.
因为年龄在[25,30)内的人数为35,所以a=35÷(0.07×5)=100.
设冬奥知识宣传小组成员年龄的中位数的估计值为x,则x在[30,35)内,且满足0.01×5+0.07×5+(x-30)×0.06=0.5,解得x≈31.7.
(2)由频率分布直方图知,小组成员年龄在[30,35),[35,40),[40,45]的人数之比为3∶2∶1,故抽取的6名志愿者中,在区间[30,35),[35,40),[40,45]中分别有3人,2人,1人,记[30,35)中的3名志愿者为A1,A2,A3,[35,40)中的2名志愿者为
B1,B2,[40,45]中的1名志愿者为C,则从6人中再随机抽取2人的所有可能有(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C),(A2,A3),(A2,B1),(A2,B2),(A2,C),(A3,B1),
(A3,B2),(A3,C),(B1,B2),(B1,C),(B2,C),共15种,至少有1人年龄在[35,40)内的情
规律方法
解决统计图表与概率综合问题的一般步骤
对点练3(2022·安徽淮南二模)为激发广大学生努力学习科学文化知识的热情,某中学团委举行了一场名为“学习航天精神,致敬航空英雄”的航天航空科普知识竞赛,满分90分,共有100名同学参赛,经过评判,这100名参赛者的得分都在[40,90]之间,其得分的频率分布直方图如图所示.
(1)根据频率分布直方图,求这100名同学得分的平均数(同一组中的数据用该组区间的中点值代表);
(2)用分层抽样的方法从成绩在[60,70),[70,80),[80,90]三组同学中抽取6名同学,从这6名同学中抽取2名作为代表参加总结
表彰大会,求这2名同学的成绩分别在[60,70),[80,90]各一名的概率.
解 (1)根据题意知(a+0.035+0.030+0.020+0.010)×10=1,解得a=0.005,所以这100名同学得分的平均数是45×0.005×10+55×0.035×10+65×
0.030×10+75×0.020×10+85×0.010×10=64.5.
(2)由条件知从[60,70)抽取3名,从[70,80)中抽取2名,从[80,90]抽取1名,分别记为a,b,c,d,e,f,从6名同学抽取2名,共有(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),
(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)15种,这2名同学的成绩分别在[60,70),[80,90]各一名的有(a,f),(b,f),(c,f)共3种,所以2名同学的成绩分别在
考点四
统计与统计案例的综合
典例突破4(2020·全国Ⅲ·理18)某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
空气质量等级 锻炼人次
[0,200] (200,400] (400,600]
1(优) 2 16 25
2(良) 5 10 12
3(轻度污染) 6 7 8
4(中度污染) 7 2 0
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关
锻炼人次 ≤400 >400
空气质量好
空气质量不好
P(K2≥k0) 0.050 0.010 0.001
k0 3.841 6.635 10.828
解 (1)由所给数据,该市一天的空气质量等级为1,2,3,4的概率的估计值如下表:
空气质量等级 1 2 3 4
概率的估计值 0.43 0.27 0.21 0.09
(2)一天中到该公园锻炼的平均人次的估计值为
(3)根据所给数据,可得2×2列联表:
锻炼人次 ≤400 >400
空气质量好 33 37
空气质量不好 22 8
由于5.820>3.841,故有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.
规律方法
1.频率分布直方图中,每个小长方形的面积表示相应各组的频率,不是小长方形的高表示频率,平均数是每个小长方形的面积与对应小长方形底边中点的横坐标的乘积之和.
2.进行独立性检验时,注意提出的假设是X和Y相互独立,即两者无关.
对点练4 某公司为了节能减排,将办公室里的旧空调更换成了节能空调,并统计了使用节
能空调之前和之后各20天里每天的用电量(单位:kW·h),绘制成如下的茎叶图:
(1)从这40天中随机选一天,求这一天的用电量大于或等于50 kW·h的概率;
(2)求这40天办公室用电量的中位数m,并完成下面的2×2列联表;
类型 不超过m 超过m
使用旧空调
使用节能空调
(3)根据(2)中的列联表,能否有95%的把握认为节能空调起到了节能作用
P(K2≥k0) 0.050 0.010 0.005
k0 3.841 6.635 7.879
解 (1)这40天中用电量大于或等于50 kW·h的天数为8,所以从这40天中随机选一天,这一天的用电量大于或等于50 kW·h的概率为
列联表如下:
类型 不超过m 超过m
使用旧空调 7 13
使用节能空调 13 7
故没有95%的把握认为节能空调起到了节能作用.
考点五
统计、统计案例与概率的综合
典例突破5(2022·山西吕梁模拟预测)某公司生产医用外科口罩,由于国内疫情得到了较好的控制,口罩的销量有所下降,因此该公司逐步调整了口罩的产量,下图是2021年5~11月份该公司口罩产量(单位:万箱):
由散点图可知产量y(单位:万箱)与月份x具有线性相关关系.
(1)求产量y关于月份x的线性回归方程,并预测12月份的产量;
(2)某单位从该公司共购买了6箱口罩(其中有4箱5月份生产,2箱6月份生产),随机分发给单位研发部门和销售部门使用,其中研发部门4箱,销售部门2箱,使用中发现5月份生产的口罩不符合质量要求,单位要求该公司给予更换,求分发给销售部门的2箱口罩中至多有1箱需要更换的概率.
附:回归直线y=bx+a的斜率和截距的最小二乘估计分别为
(2)记5月份生产的4箱为A,B,C,D,6月份生产的2箱为a,b,则从6箱中抽取2箱有(A,B),(A,C),(A,D),(A,a),(A,b),(B,C),(B,D),(B,a),(B,b),(C,D),(C,a),(C,b),
(D,a),(D,b),(a,b),共15种情况,其中至多有1箱为5月份生产的有9种,故所求
规律方法
1.求回归直线方程的一般步骤:
2.独立性检验的步骤:列表、计算、检验.
3.古典概型是基本事件个数有限,每个基本事件发生的概率相等的一种概率模型,计算概率时,要先判断再计算.
对点练5(2022·甘肃武威一中模拟)为提升学生身体素质,鼓励学生参加体育运动,某学校随机抽查了200名学生,统计他们在寒假期间每天参加体育运动的时间,并把每天参加体育运动时间超过30分钟的记为“运动达标”,不超过30分钟的记为“运动欠佳”,统计情况如下:
(1)完成下面2×2列联表,并判断能否在犯错误的概率不超过0.025的前提下认为“运动达标”与“性别”有关
性别 运动达标 运动欠佳 总计
男生
女生
总计
(2)现从“运动欠佳”的学生中按性别用分层抽样的方法抽取5人,再从这5人中任选2人进行体育运动指导,求选中的2人都是女生的概率.
参考数据:
P(K2≥k0) 0.25 0.10 0.05 0.025 0.010
k0 1.323 2.706 3.841 5.024 6.635
解 (1)列联表为
性别 运动达标 运动欠佳 总计
男生 68 32 100
女生 52 48 100
总计 120 80 200
所以能在犯错误的概率不超过0.025的前提下认为“运动达标”与“性别”有关.
(2)由(1)知“运动欠佳”的男生、女生分别有32人和48人,按分层抽样的方法从中抽取5人,则男生、女生分别抽到2人和3人,记两名男生分别为A,B,三名女生分别为a,b,c.
则从5人中任选2人有(A,B),(A,a),(A,b),(A,c),(B,a),(B,b),(B,c),(a,b),(a,c),(b,c)共10种情况,其中两人全是女生的情况有(a,b),(a,c),(b,c)共3种,
培优拓展
问题提出
1.非线性回归问题的解题思路:
(1)把非线性回归方程转化为线性回归方程,求出线性回归系数,得出线性回归方程,最后转化为非线性回归方程.
(2)准确计算,读懂题意,会预测预报变量的值.
2.非线性回归方程转化为线性回归方程的常见类型:
①幂函数曲线:y=axb,两边取对数可得ln y=ln a+bln x,令μ=ln y,v=ln x,
c=ln a,则μ=bv+c;
②指数曲线:y=aebx,两边取对数可得ln y=ln a+bx,令μ=ln y,c=ln a,则μ=bx+c;
μ=bv+c;
④对数曲线:y=a+bln x,令v=ln x,则y=a+bv.
结论应用
【例1】 (2022·四川绵阳三模)随着科技进步,近年来,我国新能源汽车产业迅速发展.以下是中国汽车工业协会2022年2月公布的近六年我国新能源乘用车的年销售量数据:
年份 2016 2017 2018 2019 2020 2021
年份代码x 1 2 3 4 5 6
新能源乘用车年销售量y/万辆 50 78 126 121 137 352
(1)根据表中数据,求出y关于x的线性回归方程;(结果保留整数)
(2)请用y=menx模型拟合y与x的关系(保留两位小数),并分别利用这两个模型,求2022年我国新能源乘用车的年销售量的预测值;
(3)经计算第(2)问中模型和第(1)问中模型的R2(R2为相关指数)分别为0.87和0.71,你认为(2)中用哪个模型得到的预测值更可靠 请说明理由.
参考数据:设u=ln y,其中ui=ln yi.
参考公式:回归直线y=bx+a的斜率和截距的最小二乘估计分别为
解 (1)由表中数据得,
【例2】 (2022·湖南雅礼中学二模)为锻炼学生的综合实践能力,某市一中学组织学生对一家奶茶店的营业情况进行调查统计,得到的数据如下:
月份x 2 4 6 8 10 12
净利润 y/万元 0.9 2.0 4.2 3.9 5.2 5.1
(2)从相关系数的角度确定哪一个模型的拟合效果更好,并据此预测次年2月(计x=14)的净利润(保留1位小数).
因为r1更接近1,所以模型y=2.52ln x-0.99的拟合效果更好,则次年2月净利润为y≈2.52ln 14-0.99≈5.6(万元).
专题四 概率与统计
上篇
内容索引
01
02
03
高考小题突破6 概率与统计的基本运算
培优拓展 巧比较解决统计图表创新题中的数据分析
◎高考保分大题四 概率与统计的综合问题
04
培优拓展 巧转化速解非线性回归问题
考情分析 1.题型、题量稳定:近年来,高考对该部分的考查一般为“2小1大”,分值约22分,多为中、低档题.
2.重点突出:(1)客观题重点考查抽样方法、用样本估计总体、古典概型、几何概型、样本、数据的数字特征等,难度较低;(2)主观题以现实生活中的真实情境为背景,考察回归分析、独立性检验以及统计与概率的综合应用等,常与实际生活中的统计图表相结合,阅读量大,多为中等难度.
3.核心素养:逻辑推理、数学运算.
备考策略 1.把握关键:数据的统计与分析是统计与概率的核心,也是高考命题的重点与热点,灵活利用数据的数字特征、辨清事件的性质与类型是解决该部分问题的关键.
2.加强计算:该部分考题无论是数据的分析还是概率的求解,准确地进行运算是基础,所以要加强基本的数据处理、运算能力.
3.加强阅读能力:概率与统计问题多与社会、生活、科技等情境问题相结合,从情境中读取有用信息,并建立正确的数学模型是解决该部分问题的关键环节.
真题感悟
1.(2022·全国甲·文6)从分别写有1,2,3,4,5,6的6张卡片中无放回随机抽取2张,则抽到的2张卡片上的数字之积是4的倍数的概率为( )
答案 C
解析 从6张卡片中无放回随机抽取2张,所有可能的结果是(1,2),(1,3),
(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共15种,其中数字之积是4的倍数的结果是(1,4),(2,4),(2,6),(3,4),(4,5),(4,6)共6
2.(2022·全国乙·文4)分别统计了甲、乙两位同学16周的各周课外体育运动时长(单位:h),得如下茎叶图:
则下列结论中错误的是( )
A.甲同学周课外体育运动时长的样本中位数为7.4
B.乙同学周课外体育运动时长的样本平均数大于8
C.甲同学周课外体育运动时长大于8的概率的估计值大于0.4
D.乙同学周课外体育运动时长大于8的概率的估计值大于0.6
C
3.(2020·全国Ⅰ·理5)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(xi,yi)(i=1,2,…,20)得到下面的散点图:
由此散点图,在10 ℃至40 ℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
A.y=a+bx B.y=a+bx2 C.y=a+bex D.y=a+bln x
答案 D
解析 结合题中散点图,由图象的大致走向判断,此函数应该是对数函数模型,故应该选用的函数模型为y=a+bln x.
4.(2019·全国Ⅱ·文14)我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为 .
答案 0.98
解析 由题意,得经停该高铁站的列车的正点数约为10×0.97+20×0.98+10×0.99=39.2,其中车次数为10+20+10=40,所以经停该站高铁列车所有车次的平均正点率的估计值为 =0.98.
5.(2022·全国甲·文17)甲、乙两城之间的长途客车均由A和B两家公司运营,为了解这两家公司长途客车的运行情况,随机调查了甲、乙两城之间的500个班次,得到下面列联表:
公司 准点班次数 未准点班次数
A 240 20
B 210 30
(1)根据上表,分别估计这两家公司甲、乙两城之间的长途客车准点的概率;
(2)能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关
P(K2≥k0) 0.100 0.050 0.010
k0 2.706 3.841 6.635
解 (1)A公司一共调查了260个班次的长途客车,其中有240个班次的长途客车准点,故A公司的长途客车准点的概率为 ≈0.923,B公司一共调查了240个班次的长途客车,其中有210个班次的长途客车准点,故B公司的长途客车准点的概率为 =0.875.
(2)根据已知数据得到列联表如下:
公司 准点班次数 未准点班次数 合计
A 240 20 260
B 210 30 240
合计 450 50 500
所以有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关.
知识精要
1.样本数据x1,x2,…,xn的数字特征
2.频率分布直方图
(1)小长方形的面积等于频率,各小长方形的面积的总和等于1.
(2)最高的小长方形底边中点的横坐标即是众数.
(3)中位数左边和右边的小长方形的面积和是相等的.
(4)平均数等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和(同一组中的数据用该组区间的中点值为代表).
误区警示
(1)频率分布直方图中纵轴表示的是 ,不是频率.
(2)每组的频率等于该组小长方形的面积,不是该组小长方形的高.
3.变量间的相关关系
(1)如果散点图中的点从整体上看大致分布在一条直线的附近,那么我们说变量x和y具有线性相关关系.
(2)线性回归方程:若变量x与y具有线性相关关系,有n个样本数据
当r>0时,表示两个变量正相关;当r<0时,表示两个变量负相关.|r|越接近1,表明两个变量相关性越强;当|r|接近0时,表明两个变量几乎不存在相关性.
名师点析
4.独立性检验
对于取值分别是{x1,x2}和{y1,y2}的分类变量X和Y,其样本频数列联表是:
X Y 总计
y1 y2
x1 a b a+b
x2 c d c+d
总计 a+c b+d n
名师点析
K2的观测值k越大,说明“两个分类变量有关系”的可能性越大.
5.概率的基本性质及常见概率的计算
(1)随机事件的概率:0
(3)若事件A,B对立,则P(A∪B)=P(A)+P(B)=1.
(4)古典概型的特点:有限性,等可能性;
需要重视的关键点
名师点析
常用排列、组合知识计算基本事件个数.
(7)相互独立事件同时发生的概率:P(AB)=P(A)P(B).
特别提醒
计算概率时,先判断概率类型,再代入对应公式计算.
(6)概率的估计值:当试验次数足够多时,常用频率估计概率.
高考小题突破6
考点一
统计图表及其应用
典例突破1(2021·全国甲·文2)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
答案 C
解析 该地农户家庭年收入低于4.5万元的农户比率估计为(0.02+0.04)×1=6%,A正确;
该地农户家庭年收入不低于10.5万元的农户比率估计为(0.04+0.02+0.02+0.02)×1=10%,B正确;
该地农户家庭年收入的平均值为0.02×3+0.04×4+0.1×5+0.14×6+0.2×7+0.2×8+0.1×9+0.1×10+0.04×11+0.02×12+0.02×13+0.02×14=7.68,C不正确;
该地农户家庭年收入介于4.5万元至8.5万元之间的比率为(0.1+0.14+0.2+0.2)×1=64%,D正确.
规律方法
统计图表的使用
(1)数据读取:读取数据时要结合问题背景理解图表意义,特别是频率分布直方图中的纵坐标,应为频率与组距的商.
(2)数据分析:数据的分析应遵循“用样本估计总体”的思想,抓住数据的数字特征.
对点练1(2022·陕西二模)小张一星期的总开支分布如图1所示,一星期的食品开支如图2所示,则小张一星期的肉类开支占总开支的百分比约为( )
图1
图2
A.10% B.8% C.5% D.4%
答案 A
解析 由题图知,小张一星期的食品开支为30+40+100+80+50=300(元),其中肉类开支为100元,占食品开支的 ,而食品开支占总开支的30%,所以小张一星期的肉类开支占总开支的百分比为30%× =10%.故选A.
考点二
回归分析与独立性检验
典例突破2(1)在一项调查中有两个变量x和y,下图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为y关于x的回归方程的函数类型是( )
A.y=a+bx B.y=p+qcx(q>0)
C.y=m+nx2(n>0) D.y=c+d
(2)(2022·重庆三模)北京2022年冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”一亮相,好评不断.为了研究“冰墩墩”与“雪容融”在不同性别的人群中受欢迎程度是否存在差异,某机构随机调查了100人,得到如下2×2列联表:
性别 男 女 总计
更喜欢“冰墩墩” 25 15 40
更喜欢“雪容融” 25 35 60
总计 50 50 100
P(K2≥k0) 0.100 0.050 0.010 0.001
k0 2.706 3.841 6.635 10.828
则下列说法正确的是( )
A.有95%以上的把握认为“对两个吉祥物的喜好倾向与性别无关”
B.有95%以上的把握认为“对两个吉祥物的喜好倾向与性别有关”
C.在犯错误的概率不超过1%的前提下,可以认为“对两个吉祥物的喜好倾向与性别无关”
D.在犯错误的概率不超过1%的前提下,可以认为“对两个吉祥物的喜好倾向与性别有关”
答案 (1)D (2)B
解析 (1)散点图呈曲线,A中函数为线性函数,不合题意,故排除A;由散点图可知整体呈增长态势,且增长速度变慢.对于B,函数为指数型函数,当c>1时函数单调递增,且增长速度变快,不合题意,当0
(2)由列联表中的数据,可得k= ≈4.167>3.841,所以有95%以上的把握认为“对两个吉祥物的喜好倾向与性别有关”.故选B.
规律方法
1.非线性回归方程的求法
(1)根据原始数据作出散点图;
(2)根据散点图,选择恰当的拟合函数;
(3)做恰当变换,将其转化成线性函数,求线性回归方程;
(4)在(3)的基础上通过相应变换,即可得到非线性回归方程.
提醒:可以建立多个函数模型时,要对每个模型进行分析比较,选择最优模型.
2.独立性检验问题的解题步骤
(1)做出2×2列联表;
(2)计算随机变量K2的观测值k;
(3)查临界值,检验作答.
对点练2(1)(2022·辽宁葫芦岛二模)某生物兴趣小组为研究一种红铃虫的产卵数y与温度x(单位:℃)的关系,现收集了7组观测数据(xi,yi)(i=1,2,…,7)得到下面的散点图:
由此散点图,在20 ℃至36 ℃之间,下面四个回归方程类型中最适宜作为红铃虫产卵数y和温度x的回归方程类型的是( )
A.y=a+bx
C.y=a+bex
D.y=a+bln x
(2)(2022·四川成都三模)在某大学一食品超市,随机询问了70名大学生在购买食物时是否查看营养说明,得到如下的列联表:
性别 女 男 总计
要查看营养说明 15 25 40
不查看营养说明 20 10 30
总计 35 35 70
P(K2≥k0) 0.10 0.05 0.025 0.010
k0 2.706 3.841 5.024 6.635
则下列说法正确的是( )
A.在犯错误的概率不超过0.05的前提下认为该校大学生在购买食物时要查看营养说明的人数中男生人数更多
B.在犯错误的概率不超过0.010的前提下认为该校女大学生在购买食物时要查看营养说明的人数与不查看营养说明的人数比为
C.在犯错误的概率不超过0.025的前提下认为性别与是否查看营养说明有关系
D.在犯错误的概率不超过0.010的前提下认为性别与是否查看营养说明有关系
答案 (1)C (2)C
解析 (1)由散点图可以看出此函数是增函数,且增长速度越来越快,所以y=a+bex最适宜作为红铃虫产卵数y和温度x的回归方程类型.故选C.
(2)由列联表可得k= ≈5.833>5.024,所以在犯错误的概率不超过0.025的前提下认为性别与是否查看营养说明有关系.故选C.
考点三
古典概型
典例突破3(1)(2021·全国甲·文10)将3个1和2个0随机排成一行,则2个0不相邻的概率为( )
A.0.3 B.0.5 C.0.6 D.0.8
(2)(2022·全国乙·文14)从甲、乙等5名同学中随机选3名参加社区服务工作,则甲、乙都入选的概率为 .
解析 (1)将3个1和2个0随机排成一行,共有11100,00111,01110,11010,11001,
10110,10011,10101,01101,01011,10种排法,2个0不相邻的排法共有01110,11010,10110,10101,01101,01011,6种排法,故所求的概率为
(2)设除甲、乙外,其余三名同学为A,B,C.
从甲、乙等5名同学中随机选3名,则所有的可能结果为(甲,乙,A),(甲,乙,B),
(甲,乙,C),(甲,A,B),(甲,B,C),(甲,A,C),(乙,A,B),(乙,B,C),(乙,A,C),(A,B,C),共10个.甲、乙都入选的可能结果为(甲,乙,A),(甲,乙,B),(甲,乙,C),有3个.由古典概型公式计算,得甲、乙都入选的概率为 .
规律方法
求解古典概型的关键点
计数方法 常用到列举法、列表法、树状图等方法.
注意:1.判断事件是否与顺序相关;2.列举基本事件时,要按照一定的顺序,避免重复或遗漏
求解策略 较为复杂的计数问题,可以分解为互斥事件概率求解;也可以转化为对立事件的概率求解
对点练3(2020·全国Ⅰ·文4)设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为( )
(2)(2022·江西南昌二模)从装有3个红球和2个蓝球(除颜色外完全相同)的盒子中任取两个球,则选到的两个球颜色相同的概率为 .
解析 (1)由题意知一共有10种取法,当选A,O,C和B,O,D时符合要求,故
(2)3个红球记为a,b,c,2个蓝球记为A,B,则任取两个球有ab,ac,aA,aB,bc,bA,
bB,cA,cB,AB,共10种选法.其中颜色相同的有ab,ac,bc,AB,共4种选法.所以选
考点四
几何概型
(2)(2022·江西宜春模拟预测)如图所示,将4个全等的直角三角形拼成边长为a+b的正方形ABCD,使中间留下一个正方形EFGH.已知a=3,b=4,在正方形ABCD内随机取一点,则该点恰好取自阴影部分的概率为( )
答案 (1)B (2)B
规律方法
求解几何概型的基本步骤
(1)定型:即根据事件的性质确定概率概型;
(2)定性:准确判断几何概型中事件的度量方式,一般用长度、角度、面积或者体积表示;
(3)求量:即求解事件的度量,代入几何概型的求解公式求解.
对点练4(1)(2022·河南鲁山一中模拟)中国古代数学名著《九章算术》中记载:“圆周与其直径之比被定为3,圆中弓形面积为 a(a+c)(c为弦长,a为半径长与圆心到弦的距离之差).”据此计算,已知一个圆中弓形所对应的弦长c=6,a=1,质点M随机投入此圆中,则质点M落在该弓形内的概率为( )
(2)对称性是数学美的重要特征,是数学家追求的目标,也是数学发现与创造中的重要的美学因素.现用随机模拟的方法来估算对称蝴蝶(如图中阴影区域所示)的面积,做一个边长为2 dm的正方形将其包含在内,并向该正方形内随机投掷1 000个点,已知恰有395个点落在阴影区域内,据此可估计图中对称蝴蝶的面积是 dm2.
答案 (1)B (2)1.58
培优拓展
问题提出
统计图表有频率分布直方图、茎叶图、折线图、条形图、饼形图、雷达图等,它们广泛应用于实际生活中,也是历年高考的热点,求解此类问题的关键是由图表读出有用的数据,再根据数据进行分析.
数据的对比分析要抓住其数字特征,主要有以下三个角度的分析:
(1)平均数:反应这组数字的平均取值水平;
(2)方差:反应这组数字取值的离散程度,方差越大,说明取值越分散.
(3)变化趋势:主要涉及数据的增大或减小、数据变化的幅度大小等.
结论应用
类型一频率分布直方图
【例1】 某地计划引进一批果树树苗提供给果农种植.为了解果树树苗的生长情况,现从甲、乙两个品种中各随机抽取了100株,进行高度测量,并将高度数据制作成了如图所示的频率分布直方图.由频率分布直方图求得甲、乙两个品种高度的平均值都是66.5,用样本估计总体,则下列描述正确的是( )
A.甲品种的平均高度高于乙品种,且乙品种比甲品种长得整齐
B.乙品种的平均高度高于甲品种,且甲品种比乙品种长得整齐
C.甲、乙品种的平均高度差不多,且甲品种比乙品种长得整齐
D.甲、乙品种的平均高度差不多,且乙品种比甲品种长得整齐
甲品种
乙品种
答案 D
解析 由题知,甲、乙两个品种高度的平均值均为66.5,即甲、乙品种的平均高度差不多,从频率分布直方图可以看出乙品种比甲品种高度更集中,长得整齐.故选D.
类型二折线图
【例2】 如图所示为2021年3月到2022年3月某地居民消费价格的涨跌幅情况.
居民消费价格涨跌幅
关于这个时间段的折线图,有下列说法:
①所有月份的同比增长率都是正数;
②环比增长率为正数的月份比为负数的月份多;
③2021年9月到10月的同比增长率的增幅等于10月到11月的同比增长率的增幅;
④同比增长率的极差为0.9.
其中正确说法的个数为( )
A.1 B.2 C.3 D.4
答案 C
解析 ①显然是正确的;
②环比增长率为正数的有6个月,为负数的有5个月,故②正确;③2021年9月到10月的同比增长率的增幅为1.5-0.7=0.8,10月到11月的同比增长率的增幅为2.3-1.5=0.8,所以③的说法是正确的;④同比增长率的极差为2.3-0.4=1.9,所以④的说法是错误的.故选C.
类型三扇形图
【例3】 某商场开通三种平台销售商品,五一期间这三种平台的数据如图1所示.该商场为了解消费者对各平台销售方式的满意程度,用分层抽样的方法抽取了6%的顾客进行满意度调查,得到的数据如图2所示.下列说法正确的是( )
图1
图2
A.样本中对平台一满意的消费者人数约为700
B.估计总体中对平台二满意的消费者人数为18
C.样本中对平台一和平台二满意的消费者总人数约为60
D.若样本中对平台三满意的消费者人数为120,则m=90%
答案 C
解析 对于A,样本中对平台一满意的人数约为2 000×6%×35%=42,故选项A错误;对于B,总体中对平台二满意的人数约为1 500×20%=300,故选项B错误;对于C,样本中对平台一和平台二满意的总人数约为
2 000×6%×35%+1 500×6%×20%=60,故选项C正确;对于D,对平台三的满意率为 =80%,所以m=80%,故选项D错误.故选C.
类型四其他图表
【例4】 某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15 ℃,B点表示四月的平均最低气温约为5 ℃.下面叙述正确的个数为( )
①七月的平均温差比一月的平均温差大;②十月的平均温差最大;③三月和十一月的平均最高气温基本相同;④平均最高气温在15 ℃到20 ℃之间的月份至少有4个.
A.1 B.2 C.3 D.4
答案 B
解析 对于①,七月的平均最高气温点与平均最低气温点间的距离大于一月的平均最高气温点与平均最低气温点间的距离,所以七月的平均温差比一月的平均温差大,故①正确;对于②,十月的平均温差明显小于七月,故②不正确;对于③,三月和十一月的平均最高气温均为10 ℃,故③正确;对于④,平均最高气温在15 ℃到20 ℃之间的月份有五月、九月,共2个月份,故④不正确.故选B.
高考保分大题四
考点一
回归分析及应用
典例突破1(2022·河南焦作二模)小李准备在某商场租一间商铺开服装店,为了解市场行情,在该商场调查了20家服装店,统计得到了它们的面积x(单位:m2)和日均客流量y(单位:百人)的数据(xi,yi)(i=1,2,…,20),并计算
(1)求y关于x的回归直线方程;
(2)已知服装店每天的经济效益W=k +mx(k>0,m>0),该商场现有60~150 m2的商铺出租,根据(1)的结果进行预测,要使单位面积的经济效益Z最高,小李应该租多大面积的商铺
附:回归直线y=bx+a的斜率和截距的最小二乘估计分别为:
则f(x)=g(t)=0.15t-7.5t2=-7.5×(t-0.01)2+0.000 75,
当t=0.01,即x=100时,f(x)取最大值,
又因为k>0,m>0,所以此时Z也取最大值,
因此,小李应该租100 m2的商铺.
规律方法
线性回归分析问题的类型及解题方法
1.求回归直线方程:
2.对变量值预测:
(1)若已知回归直线方程(方程中无参数),进而预测时,可以直接将数值代入求得特定要求下的预测值;
(2)若回归直线方程中有参数,则根据回归直线一定经过点( ),求出参数值,得到回归直线方程,进而完成预测.
对点练1(2022·安徽合肥二模)据统计,截止到2020年底,我国私人汽车拥有量超过24千万辆.下图是2011年至2020年十年间我国私人汽车拥有量y(单位:千万辆)的折线图.
(注:年份代码1~10分别对应年份2011~2020)
(1)由折线图能够看出,可以用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(2)建立y关于t的线性回归方程(系数精确到0.01),并预测2023年我国私人汽车拥有量.
相关系数r≈0.998 8,说明y与t的线性相关性很高,
所以可以用线性回归模型拟合y与t的关系.
据此可以预测,2023年我国私人汽车拥有量将达到30.05千万辆.
考点二
独立性检验及其应用
典例突破2(2021·全国甲·文17)甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:
机床 产品质量 合计
一级品 二级品
甲机床 150 50 200
乙机床 120 80 200
合计 270 130 400
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少
(2)能否在犯错误的概率不超过0.01的情况下认为甲机床的产品质量与乙机床的产品质量有差异
P(K2≥k0) 0.050 0.010 0.001
k0 3.841 6.635 10.828
所以在犯错误的概率不超过0.01的情况下认为甲机床的产品质量与乙机床的产品质量有差异.
解题技巧
独立性检验的关键
(1)根据2×2列联表准确计算K2的观测值k,若2×2列联表没有列出来,要先列出此表;
(2)K2的观测值k越大,对应假设事件H0成立(两类变量相互独立)的概率越小,H0不成立的概率越大.
对点练2(2022·云南二模)某地举行演讲比赛,有60名选手参加了比赛,评委从演讲内容、演讲能力、演讲效果、综合印象四个分项为选手打分,各项成绩均按百分制计,然后再按演讲内容占40%,演讲能力占40%,演讲效果占15%,综合印象占5%,计算选手的比赛总成绩(百分制).
甲、乙两名选手的单项成绩如下表:
选手 演讲内容 演讲能力 演讲效果 综合印象
甲 85 90 85 90
乙 87 88 90 87
(1)分别计算甲、乙两名选手的比赛总成绩;
(2)比赛结束后,对参赛的60名选手的性别和获奖情况进行统计,情况如下表:
性别 获奖 未获奖
男 10 15
女 15 20
能否有90%的把握认为这次演讲比赛,选手获奖与选手性别有关
P(K2≥k0) 0.15 0.10 0.010 0.001
k0 2.072 2.706 6.635 10.828
解 (1)甲选手的比赛总成绩:85×40%+90×40%+85×15%+90×5%=87.25(分).
乙选手的比赛总成绩:87×40%+88×40%+90×15%+87×5%=87.85(分).
∴没有90%的把握认为选手获奖与选手性别有关.
考点三
统计图表与概率的综合
典例突破3(2022·江西萍乡二模)第24届冬奥会于2022年2月4日至2月20日在北京举行,组委会为普及冬奥知识,面向全市征召a名志愿者成立冬奥知识宣传小组,现把该小组成员按年龄分成[20,25),[25,30),[30,35),[35,40),
[40,45]这5组,得到的频率分布直方图如图所示,已知年龄在[25,30)内的人数为35.
(1)求m和a的值,并估计该冬奥知识宣传小组成员年龄的中位数(精确到0.1);
(2)若用分层抽样的方法从年龄在[30,35),[35,40),[40,45]内的志愿者中抽取6名参加某社区的宣传活动,再从这6名志愿者中随机抽取2名去该社区的一所高中组织一次冬奥知识宣讲,求这2名志愿者中至少有1人年龄在[35,40)内的概率.
解 (1)由频率分布直方图知,(0.01+m+0.06+0.04+0.02)×5=1,解得m=0.07.
因为年龄在[25,30)内的人数为35,所以a=35÷(0.07×5)=100.
设冬奥知识宣传小组成员年龄的中位数的估计值为x,则x在[30,35)内,且满足0.01×5+0.07×5+(x-30)×0.06=0.5,解得x≈31.7.
(2)由频率分布直方图知,小组成员年龄在[30,35),[35,40),[40,45]的人数之比为3∶2∶1,故抽取的6名志愿者中,在区间[30,35),[35,40),[40,45]中分别有3人,2人,1人,记[30,35)中的3名志愿者为A1,A2,A3,[35,40)中的2名志愿者为
B1,B2,[40,45]中的1名志愿者为C,则从6人中再随机抽取2人的所有可能有(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C),(A2,A3),(A2,B1),(A2,B2),(A2,C),(A3,B1),
(A3,B2),(A3,C),(B1,B2),(B1,C),(B2,C),共15种,至少有1人年龄在[35,40)内的情
规律方法
解决统计图表与概率综合问题的一般步骤
对点练3(2022·安徽淮南二模)为激发广大学生努力学习科学文化知识的热情,某中学团委举行了一场名为“学习航天精神,致敬航空英雄”的航天航空科普知识竞赛,满分90分,共有100名同学参赛,经过评判,这100名参赛者的得分都在[40,90]之间,其得分的频率分布直方图如图所示.
(1)根据频率分布直方图,求这100名同学得分的平均数(同一组中的数据用该组区间的中点值代表);
(2)用分层抽样的方法从成绩在[60,70),[70,80),[80,90]三组同学中抽取6名同学,从这6名同学中抽取2名作为代表参加总结
表彰大会,求这2名同学的成绩分别在[60,70),[80,90]各一名的概率.
解 (1)根据题意知(a+0.035+0.030+0.020+0.010)×10=1,解得a=0.005,所以这100名同学得分的平均数是45×0.005×10+55×0.035×10+65×
0.030×10+75×0.020×10+85×0.010×10=64.5.
(2)由条件知从[60,70)抽取3名,从[70,80)中抽取2名,从[80,90]抽取1名,分别记为a,b,c,d,e,f,从6名同学抽取2名,共有(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),
(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)15种,这2名同学的成绩分别在[60,70),[80,90]各一名的有(a,f),(b,f),(c,f)共3种,所以2名同学的成绩分别在
考点四
统计与统计案例的综合
典例突破4(2020·全国Ⅲ·理18)某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
空气质量等级 锻炼人次
[0,200] (200,400] (400,600]
1(优) 2 16 25
2(良) 5 10 12
3(轻度污染) 6 7 8
4(中度污染) 7 2 0
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关
锻炼人次 ≤400 >400
空气质量好
空气质量不好
P(K2≥k0) 0.050 0.010 0.001
k0 3.841 6.635 10.828
解 (1)由所给数据,该市一天的空气质量等级为1,2,3,4的概率的估计值如下表:
空气质量等级 1 2 3 4
概率的估计值 0.43 0.27 0.21 0.09
(2)一天中到该公园锻炼的平均人次的估计值为
(3)根据所给数据,可得2×2列联表:
锻炼人次 ≤400 >400
空气质量好 33 37
空气质量不好 22 8
由于5.820>3.841,故有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.
规律方法
1.频率分布直方图中,每个小长方形的面积表示相应各组的频率,不是小长方形的高表示频率,平均数是每个小长方形的面积与对应小长方形底边中点的横坐标的乘积之和.
2.进行独立性检验时,注意提出的假设是X和Y相互独立,即两者无关.
对点练4 某公司为了节能减排,将办公室里的旧空调更换成了节能空调,并统计了使用节
能空调之前和之后各20天里每天的用电量(单位:kW·h),绘制成如下的茎叶图:
(1)从这40天中随机选一天,求这一天的用电量大于或等于50 kW·h的概率;
(2)求这40天办公室用电量的中位数m,并完成下面的2×2列联表;
类型 不超过m 超过m
使用旧空调
使用节能空调
(3)根据(2)中的列联表,能否有95%的把握认为节能空调起到了节能作用
P(K2≥k0) 0.050 0.010 0.005
k0 3.841 6.635 7.879
解 (1)这40天中用电量大于或等于50 kW·h的天数为8,所以从这40天中随机选一天,这一天的用电量大于或等于50 kW·h的概率为
列联表如下:
类型 不超过m 超过m
使用旧空调 7 13
使用节能空调 13 7
故没有95%的把握认为节能空调起到了节能作用.
考点五
统计、统计案例与概率的综合
典例突破5(2022·山西吕梁模拟预测)某公司生产医用外科口罩,由于国内疫情得到了较好的控制,口罩的销量有所下降,因此该公司逐步调整了口罩的产量,下图是2021年5~11月份该公司口罩产量(单位:万箱):
由散点图可知产量y(单位:万箱)与月份x具有线性相关关系.
(1)求产量y关于月份x的线性回归方程,并预测12月份的产量;
(2)某单位从该公司共购买了6箱口罩(其中有4箱5月份生产,2箱6月份生产),随机分发给单位研发部门和销售部门使用,其中研发部门4箱,销售部门2箱,使用中发现5月份生产的口罩不符合质量要求,单位要求该公司给予更换,求分发给销售部门的2箱口罩中至多有1箱需要更换的概率.
附:回归直线y=bx+a的斜率和截距的最小二乘估计分别为
(2)记5月份生产的4箱为A,B,C,D,6月份生产的2箱为a,b,则从6箱中抽取2箱有(A,B),(A,C),(A,D),(A,a),(A,b),(B,C),(B,D),(B,a),(B,b),(C,D),(C,a),(C,b),
(D,a),(D,b),(a,b),共15种情况,其中至多有1箱为5月份生产的有9种,故所求
规律方法
1.求回归直线方程的一般步骤:
2.独立性检验的步骤:列表、计算、检验.
3.古典概型是基本事件个数有限,每个基本事件发生的概率相等的一种概率模型,计算概率时,要先判断再计算.
对点练5(2022·甘肃武威一中模拟)为提升学生身体素质,鼓励学生参加体育运动,某学校随机抽查了200名学生,统计他们在寒假期间每天参加体育运动的时间,并把每天参加体育运动时间超过30分钟的记为“运动达标”,不超过30分钟的记为“运动欠佳”,统计情况如下:
(1)完成下面2×2列联表,并判断能否在犯错误的概率不超过0.025的前提下认为“运动达标”与“性别”有关
性别 运动达标 运动欠佳 总计
男生
女生
总计
(2)现从“运动欠佳”的学生中按性别用分层抽样的方法抽取5人,再从这5人中任选2人进行体育运动指导,求选中的2人都是女生的概率.
参考数据:
P(K2≥k0) 0.25 0.10 0.05 0.025 0.010
k0 1.323 2.706 3.841 5.024 6.635
解 (1)列联表为
性别 运动达标 运动欠佳 总计
男生 68 32 100
女生 52 48 100
总计 120 80 200
所以能在犯错误的概率不超过0.025的前提下认为“运动达标”与“性别”有关.
(2)由(1)知“运动欠佳”的男生、女生分别有32人和48人,按分层抽样的方法从中抽取5人,则男生、女生分别抽到2人和3人,记两名男生分别为A,B,三名女生分别为a,b,c.
则从5人中任选2人有(A,B),(A,a),(A,b),(A,c),(B,a),(B,b),(B,c),(a,b),(a,c),(b,c)共10种情况,其中两人全是女生的情况有(a,b),(a,c),(b,c)共3种,
培优拓展
问题提出
1.非线性回归问题的解题思路:
(1)把非线性回归方程转化为线性回归方程,求出线性回归系数,得出线性回归方程,最后转化为非线性回归方程.
(2)准确计算,读懂题意,会预测预报变量的值.
2.非线性回归方程转化为线性回归方程的常见类型:
①幂函数曲线:y=axb,两边取对数可得ln y=ln a+bln x,令μ=ln y,v=ln x,
c=ln a,则μ=bv+c;
②指数曲线:y=aebx,两边取对数可得ln y=ln a+bx,令μ=ln y,c=ln a,则μ=bx+c;
μ=bv+c;
④对数曲线:y=a+bln x,令v=ln x,则y=a+bv.
结论应用
【例1】 (2022·四川绵阳三模)随着科技进步,近年来,我国新能源汽车产业迅速发展.以下是中国汽车工业协会2022年2月公布的近六年我国新能源乘用车的年销售量数据:
年份 2016 2017 2018 2019 2020 2021
年份代码x 1 2 3 4 5 6
新能源乘用车年销售量y/万辆 50 78 126 121 137 352
(1)根据表中数据,求出y关于x的线性回归方程;(结果保留整数)
(2)请用y=menx模型拟合y与x的关系(保留两位小数),并分别利用这两个模型,求2022年我国新能源乘用车的年销售量的预测值;
(3)经计算第(2)问中模型和第(1)问中模型的R2(R2为相关指数)分别为0.87和0.71,你认为(2)中用哪个模型得到的预测值更可靠 请说明理由.
参考数据:设u=ln y,其中ui=ln yi.
参考公式:回归直线y=bx+a的斜率和截距的最小二乘估计分别为
解 (1)由表中数据得,
【例2】 (2022·湖南雅礼中学二模)为锻炼学生的综合实践能力,某市一中学组织学生对一家奶茶店的营业情况进行调查统计,得到的数据如下:
月份x 2 4 6 8 10 12
净利润 y/万元 0.9 2.0 4.2 3.9 5.2 5.1
(2)从相关系数的角度确定哪一个模型的拟合效果更好,并据此预测次年2月(计x=14)的净利润(保留1位小数).
因为r1更接近1,所以模型y=2.52ln x-0.99的拟合效果更好,则次年2月净利润为y≈2.52ln 14-0.99≈5.6(万元).
同课章节目录
