2023届高考二轮总复习课件(适用于老高考旧教材) 数学(文)专题三 立体几何 课件(共144张PPT)
文档属性
| 名称 | 2023届高考二轮总复习课件(适用于老高考旧教材) 数学(文)专题三 立体几何 课件(共144张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 17:30:37 | ||
图片预览









文档简介
(共144张PPT)
专题三 立体几何
上篇
内容索引
01
02
03
高考小题突破4 空间几何体的结构、表面积与体积
高考小题突破5 空间点、直线、平面的位置关系
培优拓展 巧设变量速求立体几何中的动态、最值问题
04
培优拓展 巧用公共点速定立体几何中的截面、交线问题
05
◎高考保分大题三 立体几何中的证明与计算
考情分析 1.题型、题量稳定:高考对该部分的考查一般为“2小1大”,分值约22分,多为中档题.
2.重点突出:
(1)客观题重点考查空间几何体的表面积与体积的求解、几何体中的线面关系等判断以及几何体与球的切、接等;
(2)主观题主要考查空间平行与垂直关系的证明、几何体体积、点到平面距离的求解为重点,多为中档解答题.
3.核心素养:直观想象、逻辑推理、数学运算.
备考策略 1.夯实基础:空间几何体的结构特征以及空间线面关系是立体几何的根本,平面图形中的平行与垂直关系是空间线面关系逻辑证明的起点、突破口.
2.掌握技巧:空间线面关系的证明,要熟练掌握相关定理,抓住平面图形的结构特征;体积与距离的求解,要注意灵活换底、分割法以及等积变换法.
3.强化转化:平面化思想是解决线面关系的基础,也是命题的重点;分割转化与等积转化是求解表面积、体积问题的重要思想.
真题感悟
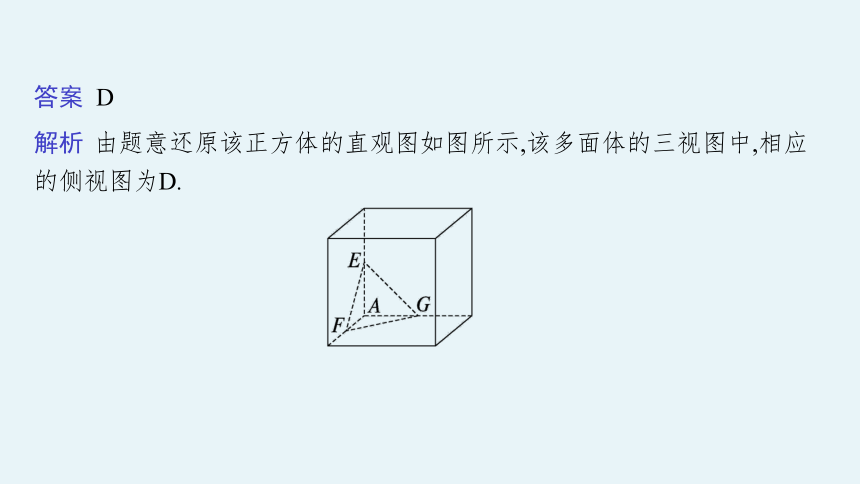
1.(2021·全国甲·文7)在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥A-EFG后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是( )
正视图
答案 D
解析 由题意还原该正方体的直观图如图所示,该多面体的三视图中,相应的侧视图为D.
答案 C
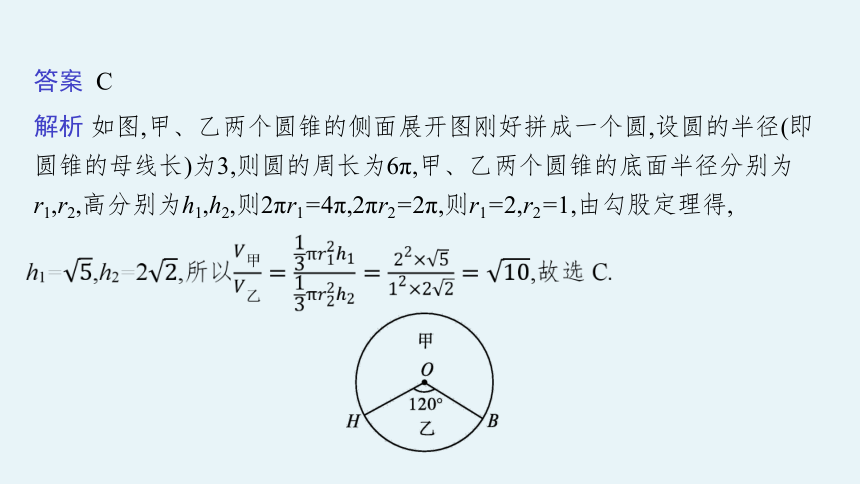
解析 如图,甲、乙两个圆锥的侧面展开图刚好拼成一个圆,设圆的半径(即圆锥的母线长)为3,则圆的周长为6π,甲、乙两个圆锥的底面半径分别为r1,r2,高分别为h1,h2,则2πr1=4π,2πr2=2π,则r1=2,r2=1,由勾股定理得,
答案 C
解析 设等边三角形ABC的边长为a,球O的半径为R,△ABC的外接圆的半径
4.(2022·全国乙·文12)已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则当该四棱锥的体积最大时,其高为( )
答案 C
5.(2021·全国甲·文14)已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为 .
答案 39π
6.(2022·全国乙·文18)如图,四面体ABCD中,AD⊥CD,AD=CD,
∠ADB=∠BDC,E为AC的中点.
(1)证明:平面BED⊥平面ACD;
(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求三棱锥F-ABC的体积.
(1)证明 ∵AD=CD,∠ADB=∠BDC,BD=BD,∴△ABD≌△CBD.∴AB=BC.又E为AC的中点,∴BE⊥AC.∵AD=CD,且E为AC的中点,∴DE⊥AC.又DE∩BE=E,∴AC⊥平面BED.∵AC 平面ACD,∴平面BED⊥平面ACD.
(2)解 ∵AB=BC=2,∠ACB=60°,∴△ABC为等边三角形.
知识精要
1.空间几何体的表面积与体积
表面积=侧面积+底面积
误区警示
2.直线、平面平行的判定及其性质
(1)线面平行的判定定理:a α,b α,a∥b a∥α.
(2)线面平行的性质定理:a∥α,a β,α∩β=b a∥b.
(3)面面平行的判定定理:a β,b β,a∩b=P,a∥α,b∥α α∥β.
(4)面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b a∥b.
易漏掉线在面内这个条件
3.直线、平面垂直的判定及其性质
(1)线面垂直的判定定理:m α,n α,m∩n=P,l⊥m,l⊥n l⊥α.
(2)线面垂直的性质定理:a⊥α,b⊥α a∥b.
(3)面面垂直的判定定理:a β,a⊥α α⊥β.
(4)面面垂直的性质定理:α⊥β,α∩β=l,a α,a⊥l a⊥β.
漏掉此处条件,a⊥β还成立吗
误区警示
上述八个定理成立的条件,每一个条件都缺一不可.
4.空间中点到平面的距离的求法
(1)定义法:过点向平面作垂线,点与垂足的距离.
(2)“等积法”:求解点到平面的距离常转化为锥体的高,利用三棱锥体积公式求点到平面的距离.
转化与化归思想,“换底”是为了能求出体积,底面上的高能求出是关键
常用结论
高考小题突破4
考点一
空间几何体的三视图
典例突破1(1)(2022·浙江二模)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图是( )
(2)(2022·宁夏六盘山二模)如图,网格纸中小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体中最长的棱长为( )
答案 (1)C (2)C
解析 (1)将几何体各顶点字母标记如图,从左侧观察,得到如图所示的侧视图,其中,对角线DE被几何体左侧面遮挡,应当为虚线,故选C.
(2)该几何体为三棱锥A-BCD,三棱锥A-BCD是由以下四棱锥A-BCDE截去三棱锥A-BDE所剩下的部分,
由于AE=DE=BC=2,EB=DC=4,
解题技巧
解决三视图问题的解题思路
由直观图确 定三视图 (1)要根据三视图的含义及画法和摆放规则确认.
(2)要熟悉常见几何体的三视图
由三视图 还原到直 观图 (1)根据俯视图确定几何体的底面.
(2)根据正视图或侧视图确定几何体的侧棱与侧面的特征,调整实线和虚线所对应的棱、面的位置.
(3)确定几何体的直观图形状
对点练1(1)(2022·甘肃兰州模拟)如图所示,在网格上小正方形的边长为1,粗实线画出的是某多面体的三视图,若此多面体的所有顶点均可以放置在一个正方体的各面内,则此正方体的对角线长为( )
(2)在三棱锥P-ABC中,底面ABC是锐角三角形,PC垂直于平面ABC,若取垂直于平面PAC的方向为正视图的方向,其三视图中正视图和侧视图如图所示,则棱PB的长为 .
解析 (1)如图所示,由已知三视图可以看出,直观图中各个顶点在正方体的面的中心位置,其中AB为正视图中两个小正方形的边长,即AB=2,所以可以得到正方体的棱长为2,所以正方体的体对角线长为
(2)根据正视图可知,PC=4,B点在AC的投影位于AC的中点,不妨设其为H,可得AH=HC=2,
考点二
空间几何体的表面积和体积
考向1空间几何体的侧面积和表面积
典例突破2(1)(2022·安徽宣城二模)刘徽是我国古代杰出的数学家.他将底面是直角三角形的直三棱柱称为“堑堵”,将
底面为矩形且一条侧棱垂直于底面的四棱
锥称为“阳马”.已知某“堑堵”与某“阳马”组
合而成的几何体的三视图如图所示,则该
几何体的表面积是( )
(2)(2022·安徽巢湖一中模拟)已知某几何体的三视图如图所示,则该几何体的表面积为( )
A.168+6π B.132+6π
C.168+24π D.132+24π
答案 (1)B (2)A
解析 (1)由三视图还原几何体如图所示.
由题意易知,四边形ABED为正方形,四边形BCFE为矩形,且
(2) 由三视图知该几何体为长方体中去掉一个圆锥体,如图所示,
所以圆锥底面半径为3,母线长为5,侧面积为5×3×π=15π,底面积为9π,则几何体的表面积为2×6×6+4×6×4+15π-9π=168+6π.
故选A.
解题技巧
求几何体表面积的方法
基本思路 将立体几何问题转化为平面图形问题,即空间图形平面化
分割法 求不规则几何体的表面积时,通常将所给几何体分割成柱、锥、台体、球,先求这些柱、锥、台体、球的表面积,再通过求和或作差求得所给几何体的表面积
对点练2(1)(2022·黑龙江齐齐哈尔一模)如图所示,网格中小正方形的边长为1,粗线所画为一个几何体的三视图,则该几何体的表面积为( )
(2)(2022·江西临川一中模拟)将一个边长为4的正三角形以其中一边所在直线为旋转轴旋转一周,所得几何体的表面积为 .
(2) 如图所示,正三角形ABC绕边AB所在直线旋转一周,得到的几何体是两个同底等高的圆锥,
考向2空间几何体的体积
典例突破3(1)(2022·全国甲·文4)如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为( )
A.8 B.12 C.16 D.20
(2) (2022·山东潍坊模拟)某品牌暖水瓶的内胆规格如图所示,分为①②③④四个部分(水瓶内胆壁厚不计),它们分别为一个半球、一个大圆柱、一个圆台和一个小圆柱.若其中圆台部分的体积为
52π cm3,且水瓶灌满水后盖上瓶塞时水溢出
cm3,则盖上瓶塞后水瓶的最大盛水量为( )
答案 (1)B (2)A
解析 (1)该多面体的直观图如图所示,多面体是一个正方体和一个三棱柱
解题技巧
求空间几何体的体积的常用方法
公式法 对于规则的几何体的体积,可直接利用体积公式求解
等积法 等积法也称等积转化或等积变形,通过选择合适的底面来求几何体体积的一种方法,多用来解决锥体的体积,特别是三棱锥的体积
割补法 求不规则几何体的体积,常用分割或补形的思想,将不规则几何体转化为规则几何体,以易于求解
对点练3(1)(2022·陕西咸阳三模)计时沙漏制作简洁方便,也实用,该几何体是由简单几何体组合而成的封闭容器(内装一
定量的细沙),其三视图如图所示(沙漏尖端忽
略不计),则该几何体的体积为( )
(2)(2022·宁夏银川一中二模)如图所示的五面体ABCDEF,其中AB∥DC∥EF,AB=3,CD=2,EF=1,EF到平面ABCD的距离是2,AB与CD之间的距离是1,∠EAB,∠FBA,∠EDC,∠FCD均为锐角,则此五面体的体积为( )
A.2 B.3
答案 (1)A (2)A
(2) 如图,过点E作EQ⊥AB,EP⊥CD,垂足分别为Q,P.过点F作FN⊥AB,FM⊥CD,垂足分别为N,M.
连接PQ,MN.
则将几何体分为四棱锥E-AQPD,三棱柱EPQ-FMN,四棱锥F-BCMN三部分.
解析 (1)由三视图知几何体是由两个底面直径为2,高为2的圆锥组成,所以
考点三
球与几何体的切、接问题
考向1外接球
典例突破4(1)(2022·辽宁东北育才学校模拟)2020年迪拜世博会中国馆建筑外观模仿中国传统灯笼,寓意希望和光明.它的形状可视为内外两个同轴圆柱,某爱好者制作了一个中国馆的实心模型,已知模型内层底面圆的直径为12 cm,外层底面圆的直径为16 cm,且内外层圆柱的底面圆周都在一个直径为20 cm的球面上,则此模型的体积为( )
A.304π cm3 B.840π cm3
C.912π cm3 D.984π cm3
(2)(2022·新高考Ⅱ·7)已知正三棱台的高为1,上下底面的边长分别为
,其顶点都在同一球面上,则该球的表面积为( )
A.100π B.128π C.144π D.192π
答案 (1)C (2)A
(2)设外接球的半径为R,由题意得,上底面所在平面截球所得圆的半径是3,下底面所在平面截球所得圆的半径是4,
解题技巧
求多面体的外接球半径的技巧
解题依据 球的性质:任何直角所对的棱必然是球的直径
补形法 侧面为直角三角形,或正四面体,或对棱相等,或线面垂直的模型,可以还原到正方体或长方体模型中去求解
定义法 到各个顶点距离均相等的点为外接球的球心,方法是先确定有特殊底面的外接圆的圆心,再过圆心作垂直此面的垂线,则球心一定在此垂线上,最后根据其他顶点确定球心的准确位置,列关系式求解
对点练4(2022·云南二模)三棱锥P-ABC的顶点都在以PC为直径的球M的球面上,PA⊥BC.若球M的表面积为100π,PA=8,则三棱锥P-ABC的体积的最大值为( )
答案 A
解析 因为三棱锥P-ABC的顶点都在以PC为直径的球M的球面上,所以PA⊥AC,PB⊥BC,又PA⊥BC,AC∩BC=C,故PA⊥平面ABC.
因为PA∩PB=P,故BC⊥平面PAB,又AB 平面PAB,故BC⊥AB.
因为球M的表面积为100π,设球的半径为R,则4πR2=100π,解得R=5,即PC=10,
考向2内切球
典例突破5 粽子古称“角黍”,是中国传统的节庆食品,由粽叶包裹糯米等食材蒸制而成.因各地风俗不同,粽子的形状和味道也不同,某地流行的“五角粽子”,其形状可以看作所有棱长均为4 cm的正四棱锥,现在需要在粽子内部放入一颗咸蛋黄,蛋黄的形状近似地看成球,则当这个蛋黄的体积最大时,蛋黄的半径为( )
答案 B
解题技巧
解决内切问题的思路
基本步骤 (1)抓切点:要认真分析图形,明确切点的位置;
(2)做截面:作出合适的截面图;
(3)定关系:确定有关元素间的数量关系
组合体 问题 (1)球与旋转体的组合,通常作它们的轴截面解题;
(2)球与多面体的组合,通过多面体的一条侧棱和球心(或“切点”
“接点”)作出截面图
对点练5(2022·辽宁沈阳二模)现有一个侧面展开图为半圆形的圆锥,其内部放有一个小球,当小球体积最大时,该圆锥与小球的体积之比是( )
A.9∶4 B.9∶5 C.3∶2 D.3∶1
答案 A
解析 由圆锥侧面展开图为半圆,设圆锥母线为l,底面半径为R,则2πR=πl,所以l=2R,可知圆锥轴截面为正三角形,圆锥高为 R ,
又由当小球是圆锥的内切球时,小球体积最大,轴截面如图所示:设此时小球半径为r,
高考小题突破5
考点
空间直线、平面位置关系的判断
典例突破(1)(2022·山西临汾三模)已知m,n是两条不同的直线,α,β,γ是三个不同的平面,下列命题中正确的是( )
A.若α⊥β,β⊥γ,则α⊥γ
B.若m⊥α,n⊥α,则m∥n
C.若α⊥β,m α,n β,则m⊥n
D.若m∥α,n∥α,则m∥n
(2)(2020·全国Ⅱ·文16)设有下列四个命题:
p1:两两相交且不过同一点的三条直线必在同一平面内.
p2:过空间中任意三点有且仅有一个平面.
p3:若空间两条直线不相交,则这两条直线平行.
p4:若直线l 平面α,直线m⊥平面α,则m⊥l.
则下述命题中所有真命题的序号是 .
①p1∧p4 ②p1∧p2 ③( p2)∨p3
④( p3)∨( p4)
答案 (1)B (2)①③④
解析 (1)若α⊥β,β⊥γ,则α,γ可以平行、相交,故A错误;若m⊥α,n⊥α,则m∥n,故B正确;由α⊥β,m α,n β推不出m⊥n,故C错误;若m∥α,n∥α,则m,n可以平行、相交、异面,故D错误.故选B.
(2)∵p1,p4为真命题,p2,p3为假命题,∴ p2, p3为真命题,∴p1∧p4为真命题,p1∧p2为假命题,( p2)∨p3为真命题,( p3)∨( p4)为真命题.故填①③④.
解题技巧
判断空间位置关系的三种方法
定理法 借助空间直线、平面平行与垂直的判定定理和性质定理进行逻辑推理判断
反证法 当从正面入手较难时,可用反证法,推出与题设或公认的结论相矛盾的命题,进而做出判断
模型法 借助空间几何体模型,如借助长方体、正四面体等几何体模型观察线面关系,结合有关定理进行肯定或否定
对点练(1)(2022·黑龙江齐齐哈尔二模)如图是一个正方体的平面展开图,则在正方体中直线AB与CD的位置关系为( )
A.相交
B.平行
C.异面并且垂直
D.异面但不垂直
(2)(2022·陕西咸阳三模)已知直线m和平面α,β满足m⊥α,α⊥β,则( )
A.m⊥β B.m∥β或m β
C.m β D.m∥β
答案 (1)D (2)B
解析 (1) 将展开图还原成正方体,由图可知,直线AB与CD的位置关系是异面.连接CE,则CE∥AB,∠DCE或其补角即为直线AB与CD的夹角,又∠DCE=60°,所以直线AB与CD不垂直.故选D.
(2)由m⊥α,α⊥β,若m β,则m∥β,否则m β,所以m∥β或m β.故选B.
培优拓展
巧设变量速求立体几何中的动态、最值问题
立体几何中的“动态问题”是指空间中的某些点、线、面的位置是不确定的或可变的一类开放性问题,解决这类问题应该动静结合、化动为静,找到相应的几何关系,对于探究存在问题或动态范围(最值)问题,用定性分析比较难或繁时,可以引进参数,把动态问题划归为静态问题.具体地,可通过构建方程、函数或不等式等进行定量计算,以算促证.
问题提出
具体可以有以下几种解决方法:
(1)函数法:某些点、线、面的运动,必然导致某些位置关系或一些变量的变化.变量变化时会引发其他变量的变化,从而建立函数关系,将立体几何问题转化为函数问题来解决.
(2)等价转换法:动和静是相对的,在运动变化过程中,要善于寻找或构造与之相关的一些不变因素,将一些变化的点、线、面进行合理转换,实现变量与不变量的结合.
【例1】 (2022·贵州模拟)设矩形ABCD(AB>BC)的周长为20,把△ABC沿AC向△ADC折叠,AB折叠后交DC于点P,点B落在点E处,则线段AP的长度最小值为( )
结论应用
答案 D
解析 ∵四边形ABCD是矩形,且△ABC沿AC向△ADC折叠,
∴AD=EC,∠ADP=∠CEP=90°,∠APD=∠CPE,
∴△ADP≌△CEP,∴AP=CP.
设AB=x,DP=y,∴AP=CP=x-y.又∵矩形ABCD(AB>BC)的周长为20,
∴AD=10-x.
由勾股定理,可得(10-x)2+y2=(x-y)2,
∵AB>BC,∴0<10-x评析 该题通过建立目标y关于x的解析式,根据解析式的结构特征选用基本不等式求最值.
【例2】 如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,点P为线段AD1上的动点,点Q为线段B1C上的动点,则PQ长度的最小值为 .
答案 1
解析 (方法一)设P点在平面BCC1B1上的射影为H,则PH⊥QH.由题意可知PH=1.
显然当x=0,即点Q,H重合,也就是PQ⊥平面BCC1B1时,PQ取得最小值1.
(方法二)因为ABCD-A1B1C1D1是正方体,所以平面AA1D1D∥平面BB1C1C,平面AA1D1D与平面BB1C1C的距离是1,因为异面直线AD1与B1C的距离是平面AA1D1D与平面BB1C1C的距离,PQ长度的最小值是AD1与B1C的距离,是1.
评析 该题虽然有两个动点,通过平面的垂线化归到直角三角形中的线段长度,从而只需要设置一个变量即可.我们也可以根据几何体的结构特征,将问题转化为两个平面之间的距离求解.
【例3】 如图1,在矩形ABCD中,AB=3,AD=1,E为CD的中点,F为线段CE(除端点外)上的动点,如图2,将△AFD沿AF折起,点D落在点D1的位置,使平面ABD1⊥平面ABC,在平面ABD1内,过点D1作D1K⊥AB,K为垂足,则AK长度的取值范围为( )
图1
图2
答案 A
解析 过点F作FM⊥AB交AB于点M,连接FK,
设AK=t,FC=x,0则MK=3-t-x,在Rt△AD1K中,D1K2=1-t2,
在Rt△FMK中,FK2=1+(3-t-x)2,D1F=3-x,
在Rt△D1FK中,FK2+D1K2=D1F2,∴1-t2+1+(3-t-x)2=(3-x)2,化简得1-3t+tx=0,
【例4】如图所示,已知四棱锥S-ABCD的底面是边长为6的菱形,
∠BAD=60°,AC,BD相交于点O,SO⊥平面ABCD,SO=4,E是BC的中点,动点P在该棱锥表面上运动,并且总保持PE⊥AC,则动点P的轨迹的长为( )
A.3 B.7 C.13 D.8
答案 D
解析 取DC,SC的中点G,F,连接GE,FE,FG.∵E是BC的中点,
∴GE∥DB,FE∥SB,显然GE∥平面SBD,FE∥平面SBD.
又GE,FE 平面EFG,GE∩FE=E,∴平面EFG∥平面SBD.
∵SO⊥平面ABCD,AC 平面ABCD,∴SO⊥AC.
又四边形ABCD是菱形,∴DB⊥AC.
∵SO∩DB=O,∴AC⊥平面SBD,则AC⊥平面EFG,
故只要动点P在平面EFG内,即总保持PE⊥AC.
又动点P在棱锥表面上运动,∴动点P的轨迹的长即为△EFG的周长.
∵四边形ABCD为菱形,边长为6,且∠BAD=60°,
∴BD=6,则OB=OD=3.又SO=4,∴SB=SD=5,
故FE=FG= ,GE=3,∴△EFG的周长为8.故选D.
评析 确定点P的轨迹,就是把已知条件“PE⊥AC”转化为过点E与直线AC垂直的平面与棱锥表面的交线,进而确定轨迹的形状进行求解.探寻变化过程中的不变关系,是解决动态问题的常用手段.对于翻折或投影问题,若能抓住相关线或面的垂面,化空间为平面,则容易找到问题的核心.
培优拓展
巧用公共点速定立体几何中的截面、交线问题
在处理空间几何问题时,常遇到用一个平面去截几何体,判断截面的形状或求截面的周长、面积等问题.很多同学空间想象力不强,确定平面的公理运用不够熟练,遇到此类问题往往束手无策,为此,有必要总结一下画截面的方法,帮助学生又快又准地找出截面,顺利解决截面问题.
画一个平面截多面体的截面,关键是确定交线,常用的方法有:
方法1.直接连接法:当有两点在几何体的同一个面上时,连接该两点即为几何体与截面的交线.
问题提出
方法2.作平行线法:过直线与直线外一点作截面,常用到面面平行、线面平行的性质,通过该点找直线的平行线,即找到几何体与截面的交线.
方法3.作延长线找交点法:观察在同一个平面上的两点,连接并延长至另一个点所在平面,同一个平面有两点则可连线,需要注意长度的运算、比例关系,否则难以确定位置关系.
名师点析
确定截面的主要依据有:(1)平面的四个公理及推论;(2)直线和平面平行的判定和性质;(3)两个平面平行的性质;(4)球的截面的性质.
【例1】 (2022·山东临沂一模)已知正三棱台ABC-A1B1C1的上下底面边长分别为2和5,侧棱长为3,则以下底面的一个顶点为球心,半径为2的球面与此正三棱台的表面的交线长为 .
答案 2π
解析不妨设以下底面的顶点A为球心作球面.
由题意,得△ABC是边长为5的等边三角形,正三棱台的侧面均为全等的等腰梯形,如图所示,在四边形ABB1A1中,AB=5,A1B1=2,AA1=BB1=3,
结论应用
在棱AB上取BF=2,连接A1F,易知△AA1F为等边三角形,即∠A1AB=60°.同理,∠A1AC=60°.则以下底面的顶点A为球心,半径为2的球面与此正三棱台
评析 该题是球面与棱台表面的交线,需要将其转化为球的截面的性质,每段弧线的圆心角就是正三棱台侧面等腰梯形的底角或下底面正三角形的内角,所以问题的关键就是求出该扇形的圆心角.
答案 A
解析 由正四面体的棱长为2 可求得它的外接球半径是3,因为3> ,所以正四面体的一个平面与球相交的截面如图所示,△BMN是正四面体的一个面,点O1是正四面体一个平面截球面所得截面圆的圆心.O1D⊥BM,点A是BM与圆O1的交点.
则正四面体表面与球面的交线的总长度为π×4=4π.
评析 该题是球面与棱锥表面的交线,需要将其转化为球的截面的性质,问题的关键就是准确求出截面圆的半径,然后利用弧长公式和几何体的对称性求得最后结果.
【例3】 如图,在正方体ABCD-A1B1C1D1中,点E,F分别是棱B1B,B1C1的中点,点G是棱C1C的中点,则过线段AG且平行于平面A1EF的截面图形为( )
A.矩形 B.三角形
C.正方形 D.等腰梯形
答案 D
解析 取BC的中点H,连接AH,GH,由题意得GH∥EF,AH∥A1F,又GH 平面A1EF,EF 平面A1EF,∴GH∥平面A1EF,同理AH∥平面A1EF,又GH∩AH=H,GH,AH 平面AHG,∴平面AHG∥平面A1EF,连接AD1,D1G,则AD1∥GH,又A∈平面AHG,GH 平面AHG,∴AD1 平面AHG,即点A,H,G,D1确定一个平面,故过线段AG且与平面A1EF平行的截面图形为四边形AHGD1,显然为等腰梯形.
评析 该题是平面与几何体的截面问题,确定该截面与几何体各棱的交点是确定截面形状的关键.
【例4】如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,点M,N分别是A1D1,A1B1的中点,过直线BD的平面α∥平面AMN,则平面α截该正方体所得截面的面积为( )
答案 B
解析 如图所示,取B1C1的中点E,C1D1的中点F,连接EF,BE,DF,B1D1,则EF∥B1D1,B1D1∥BD,所以EF∥BD,故EF,BD在同一平面内,
连接ME,因为M,E分别为A1D1,B1C1的中点,所以ME∥AB,且ME=AB,
所以四边形ABEM是平行四边形,所以AM∥BE,
又因为BE 平面BDFE,AM 平面BDFE,
所以AM∥平面BDFE,同理AN∥平面BDFE,
因为AM∩AN=A,AM,AN 平面AMN,
所以平面AMN∥平面BDFE,即等腰梯形BDFE就是所求的截面.
评析 根据面面平行的判定定理,准确确定平面α的位置,进而确定交线,确定截面的形状,即可将问题转化为平面图形中的计算问题.
【例5】 已知四棱柱ABCD-A1B1C1D1的底面为菱形,AA1⊥底面ABCD,
AA1=6,AB=8,∠BCD=60°,点M是线段BC上靠近C的四等分点,动点N在四棱柱ABCD-A1B1C1D1的表面,且MN⊥BD1,则动点N的轨迹长度为 .
解析 因为四棱柱ABCD-A1B1C1D1的底面为菱形,AA1⊥底面ABCD,所以BB1⊥AC,BD⊥AC,又因为BB1∩BD=B,所以AC⊥平面BDD1B1,所以BD1⊥AC,故在AB上取点F,使得BF=3FA,连接MF,则MF∥AC,BD1⊥MF.
在BB1上取点G,使得BG=2GB1,
设MF与BD的交点为O,连接GO,
在△D1DB中,DD1=6,BD=8,DD1⊥BD,
所以△D1DB∽△OBG,故∠D1BD=∠OGB,
所以BD1⊥OG,又BD1⊥MF,OG∩MF=O,OG,MF 平面MFG,所以BD1⊥平面MFG.
故△MFG的边即为点N的轨迹.
高考保分大题三
考点一
证明平行关系与求几何体的体积
典例突破1(2022·全国甲·文19)小明同学参加综合实践活动,设计了一个封闭的包装盒.包装盒如图所示:底面ABCD是边长为8(单位:cm)的正方形,△EAB,△FBC,△GCD,△HDA均为正三角形,且它们所在的平面都与平面ABCD垂直.
(1)证明:EF∥平面ABCD;
(2)求该包装盒的容积(不计包装盒材料的厚度).
(1)证明 过点E作EE'⊥AB于点E',过点F作FF'⊥BC于点F',连接E'F'.
∵底面ABCD是边长为8的正方形,△EAB,△FBC均为正三角形,且它们所在的平面都与平面ABCD垂直,∴EE'⊥平面ABCD,FF'⊥平面ABCD,且EE'=FF',∴四边形EE'F'F是平行四边形,则EF∥E'F'.
∵E'F' 平面ABCD,EF 平面ABCD,
∴EF∥平面ABCD.
(2)解 过点G,H分别作GG'⊥CD,HH'⊥DA,交CD,DA于点G',H',连接F'G',
G'H',H'E',AC.
由(1)及题意可知,G',H'分别为CD,DA的中点,EFGH-E'F'G'H'为长方体,故该包装盒由一个长方体和四个相等的四棱锥组合而成.∵底面ABCD是边长为
规律方法
证明线面平行与求几何体体积的解题思路
(1)证明线面平行,一般利用线面平行的判定定理,难点是找直线在平面内的平行线:
①利用三角形的中位线找平行线证明线面平行;
②构造平行四边形,找平行线;
③利用平行线分线段成比例定理推论的逆定理证明线线平行.
(2)求几何体的体积,一般思路是围绕已知条件和要求的几何体的底和高,通过几何体的几何性质,建立已知和未知的关系,依据题意可借助方程的思想求出未知数,从而求出体积.对于三棱锥的体积,常利用等体积法进行转换.
对点练1(2022·陕西榆林三模)如图,在多面体ABCDEF中,底面ABCD是正方形,AF∥DE,AF=AD=2DE,AF⊥底面ABCD.
(1)证明:BD∥平面CEF;
(2)若AF=4,求该多面体的体积.
(1)证明 如图所示,
连接AC,交BD于点M,取CF的中点N,连接MN,NE.
因为四边形ABCD是正方形,所以点M是AC的中点,所以MN∥AF,MN= AF.
又AF∥DE,AF=2DE,所以MN∥DE,MN=DE,
故四边形MNED是平行四边形,则BD∥NE.
又BD 平面CEF,NE 平面CEF,所以BD∥平面CEF.
(2)解 设该多面体的体积为V,则V=V三棱锥C-ABF+V四棱锥C-ADEF.
因为AF⊥底面ABCD,所以AF⊥BC,
又AB⊥BC,AF∩AB=A,所以BC⊥平面ABF,同理可得CD⊥平面ADEF.因为
对点练2(2022·河南洛阳一模)已知底面为菱形的四棱锥P-ABCD中,△PAD是等边三角形,平面PAD⊥平面ABCD,E,F分别是棱PC,AB上的点.
(1)从下面①②③中选取两个作为条件,证明另一个成立.
①F是AB的中点;②E是PC的中点;③BE∥平面PDF.(只需选择一种组合进行解答即可)
(2)若AD=2,∠DAB=60°,PE=EC,求三棱锥P-BDE的体积.
解 (1)①② ③.
因为F是AB的中点,E是PC的中点,取PD的中点M,连接ME,MF,则ME∥CD,且ME= CD,又四边形ABCD为菱形,所以BF∥CD且BF= CD,所以BF∥ME且BF=ME,所以四边形BEMF为平行四边形,所以BE∥FM,又BE 平面PDF,FM 平面PDF,所以BE∥平面PDF.
②③ ①.
取PD的中点M,连接ME,MF,因为E是PC的中点,
所以ME∥CD,且ME= CD,又BF∥CD,
所以BF∥ME,
因为BE∥平面PDF,平面BEMF∩平面PDF=MF,BE 平面BEMF,所以BE∥MF,所以四边形BEMF为平行四边形,所以BF=ME,即BF= CD= AB,所以F是AB的中点.
①③ ②.
取DC的中点N,连接NB,NE,
因为F是AB的中点,所以BF∥DN且BF=DN,
所以四边形BNDF为平行四边形,所以BN∥DF,
因为BN 平面PDF,DF 平面PDF,所以BN∥平面PDF,
又BE∥平面PDF,BE∩BN=B,BE,BN 平面BEN,所以平面PDF∥平面BEN.
因为平面BEN∩平面PCD=EN,平面PDF∩平面PCD=PD,所以EN∥PD,所以E是PC的中点.
(2)取AD的中点G,连接PG,
因为△APD为等边三角形,所以PG⊥AD,又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,所以PG⊥平面ABCD,又AB=BC=CD=AD=PA=PD=2,
考点二
证明垂直关系与求几何体的体积
典例突破2(2022·宁夏石嘴山一模)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AB=PA=1,AD=2,点F是PB的中点,点E为BC上的一点.
(1)求证:AF⊥平面PBC;
(2)若三棱锥P-DEF的体积为 ,求CE的长.
(1)证明 因为四边形ABCD为矩形,所以BC⊥AB,
又因为PA⊥平面ABCD,所以PA⊥BC,因为AB 平面PAB,PA 平面PAB,PA∩AB=A,所以BC⊥平面PAB,又因为AF 平面PAB,所以BC⊥AF.又因为PA=AB,F是PB的中点,所以AF⊥PB,因为PB 平面PBC,BC 平面PBC,PB∩BC=B,所以AF⊥平面PBC.
(2)解 因为AB=PA=1,
设BE=x,
疑难突破
证明线面垂直或面面垂直,一般都会要证明线线垂直,其方法有:
(1)通过计算,运用勾股定理寻求线线垂直;
(2)利用面面垂直寻求线面垂直,从而得到线线垂直;
(3)应用等腰(等边)三角形三线合一性质,即三角形底边的中线同时是高和角平分线,得到线线垂直;
(4)应用两条平行线的性质,有一条与一个平面中的直线垂直,则另一条也与平面中的直线垂直.
对点练3(2022·四川泸州三模)已知直三棱柱ABC-A1B1C1中,D为B1C1的中点.
(1)若AB=AC=2,BC=2 ,AA1=2,求点C到平面ABD的距离;
(2)从下面①②③中选取两个作为条件,证明另外一个成立.
①A1B⊥B1C;②BD⊥B1C;③A1B1=A1C1.
解 (1)因为AB=AC=2,BC=2 ,
所以AB2+AC2=BC2,即△ABC是等腰直角三角形,AB⊥AC,所以
S△ABC= ×2×2=2.
因为该三棱柱是直棱柱,所以AA1⊥平面A1B1C1.
连接A1D,A1D 平面A1B1C1,所以AA1⊥A1D.
(2)选择①②为条件,证明③成立.
证明:连接A1D,
因为A1B⊥B1C,BD⊥B1C,A1B∩BD=B,A1B 平面A1BD,BD 平面A1BD,所以B1C⊥平面A1BD.
因为A1D 平面A1BD,所以B1C⊥A1D.
又该三棱柱是直棱柱,所以BB1⊥平面A1B1C1.
因为A1D 平面A1B1C1,所以BB1⊥A1D.
因为BB1∩B1C=B1,BB1 平面BCC1B1,B1C 平面BCC1B1,所以A1D⊥平面BCC1B1.
因为B1C1 平面BCC1B1,所以A1D⊥B1C1.
因为D为B1C1的中点,所以A1B1=A1C1.
选择①③为条件,证明②成立.
证明:连接A1D,因为A1B1=A1C1,D为B1C1的中点,所以A1D⊥B1C1.
因为该三棱柱是直棱柱,所以BB1⊥平面A1B1C1.
因为A1D 平面A1B1C1,所以BB1⊥A1D.
因为BB1∩B1C1=B1,BB1 平面BCC1B1,B1C1 平面BCC1B1,所以A1D⊥平面BCC1B1.
因为B1C 平面BCC1B1,所以A1D⊥B1C.又A1B⊥B1C,A1B∩A1D=A1,A1B 平面A1BD,A1D 平面A1BD,所以B1C⊥平面A1BD,因为BD 平面A1BD.所以BD⊥B1C.
选择②③为条件,证明①成立.
证明:连接A1D,因为A1B1=A1C1,D为B1C1的中点,所以A1D⊥B1C1.
因为该三棱柱是直棱柱,所以BB1⊥平面A1B1C1.
因为A1D 平面A1B1C1,所以BB1⊥A1D.
因为BB1∩B1C1=B1,BB1 平面BCC1B1,B1C1 平面BCC1B1,所以A1D⊥平面BCC1B1.
因为B1C 平面BCC1B1,所以A1D⊥B1C.
又BD⊥B1C,BD∩A1D=D,BD 平面A1BD,A1D 平面A1BD,所以B1C⊥平面A1BD.
因为A1B 平面A1BD,所以A1B⊥B1C.
对点练4(2021·全国乙·文18)如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM.
(1)证明:平面PAM⊥平面PBD;
(2)若PD=DC=1,求四棱锥P-ABCD的体积.
(1)证明 ∵PD⊥平面ABCD,AM 平面ABCD,
∴PD⊥AM.
又PB⊥AM,PB∩PD=P,PB 平面PBD,PD 平面PBD,∴AM⊥平面PBD.
∵AM 平面PAM,∴平面PAM⊥平面PBD.
(2)解 ∵M为BC的中点,四边形ABCD为矩形,
∵AM⊥平面PBD,BD 平面PBD,
∴AM⊥BD,则有∠MAD+∠ADB=90°,又∠BAM+∠MAD=90°,
∴∠BAM=∠ADB,又∠DAB=∠ABM=90°,
考点三
空间位置关系的证明与求点面距
典例突破3(12分)(2022·内蒙古呼和浩特·一模)如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,PA=AB=2CD=2,∠ADC=90°,点E,F分别为PB,AB的中点.
(1)求证:CE∥平面PAD;
(2)求点B到平面PCF的距离.
【评分标准—找回丢分】
【教师讲评—触类旁通】
分析1:(1)问证明CE∥平面PAD,最基本的思路就是转化,既可以在平面PAD内找出与直线CE平行的直线;也可以说明过直线CE的一个平面与平面PAD平行;无论哪种思路,都要从平面图形中的平行关系入手;
分析2:(2)问中求点B到平面PCF的距离,显然直接作出垂线段不好处理,所以借助四面体BPCF的多变性——通过变换顶点、换底面求出其体积,利用体积相等列方程求解.体现了用数字刻画几何体特征的目的,也是方程思想的应用.
规律方法
求点A到平面α的距离的方法
直接法 通过线面垂直的证明,找到点A在平面α内的投影点A',则AA'的长即为点A到平面α的距离
等积变换法 通过转换棱锥的顶点棱锥的体积不变,表示出不同顶点下棱锥的高和底面积,再根据体积相等即可求出点到面的距离
对点练5如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
(1)证明 连接B1C,ME.
因为M,E分别为BB1,BC的中点,
因此四边形MNDE为平行四边形,MN∥ED.
又MN 平面C1DE,
所以MN∥平面C1DE.
(2)解 过C作C1E的垂线,垂足为H.由已知可得DE⊥BC,DE⊥C1C,所以DE⊥平面C1CE,故DE⊥CH.从而CH⊥平面C1DE,故CH的长即为C到平面C1DE的距离.由已知可得CE=1,C1C=4,
对点练6(2022·山西吕梁一模)在直四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,AB=2,AA1=4,点E,M,N分别是C1D1,AB1,CC1的中点.
(1)求证:MN∥平面A1EA;
(2)求点N到平面A1EA的距离.
(1)证明 取A1B1的中点P,连接MP,PC1,
因为PM平行且等于C1N,所以四边形PMNC1是平行四边形.
因为点E,P都是所在边的中点,所以A1P平行且等于EC1,
所以四边形A1PC1E是平行四边形,
所以PC1∥A1E,又PC1 平面A1EA,A1E 平面A1EA,
所以PC1∥平面A1EA.
又因为P,M是所在边的中点,所以PM∥AA1,又PM 平面A1EA,AA1 平面A1EA,所以PM∥平面A1EA.
而PC1∩PM=P,且PM,PC1均在平面PMNC1中,所以平面PMNC1∥平面A1EA.
又因为MN 平面PMNC1,所以MN∥平面A1EA.
(2)解 因为MN∥平面A1EA,所以点N到平面A1EA的距离等于点M到平面A1EA的距离,因为AB=C1D1=A1D1=2,AA1=4,而E为C1D1的中点,故ED1=1,所
考点四
翻折问题
典例突破4(2022·安徽芜湖一中三模)如图所示,在矩形ATCD中,AD=8,DC=3,B为TC的中点,△TAB沿AB翻折,使得点T到达点P的位置.连接PD,PC,得到四棱锥P-ABCD,点M为PD的中点.
(1)求线段CM的长度;
(2)若平面PAD⊥平面ABCD,求三棱锥P-ABD的体积.
(2) 取AD的中点O,连接BO,PO,则BO⊥AD,又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,所以BO⊥平面PAD,则BO⊥OP,
误区警示
翻折问题中的误区
平面图形翻折后成为空间图形,翻折后还在同一个平面上的线线关系不发生变化,不在同一个平面上的可能发生变化.解决这类问题就是要根据这些变与不变,去研究翻折以后的空间图形中的线面关系和各类几何量的度量值.
对点练7(2022·四川攀枝花二模)如图1,在直角梯形ABCD中,AD∥BC,AB⊥AD,点E为BC的中点,点F在AD上,EF∥AB,BC=EF=DF=4,将四边形CDFE沿EF边折起,如图2.
(1)证明:图2中的AE∥平面BCD;
(2)在图2中,若AD=2 ,求该几何体的体积.
图1
图2
(1)证明 取DF的中点G,连接AG,EG,CG.因为CE∥GF,CE=GF,所以四边形CEFG是平行四边形,所以CG∥EF∥AB且CG=EF=AB,
所以四边形ABCG是平行四边形,所以AG∥BC.因为AG 平面BCD,且BC 平面BCD,所以AG∥平面BCD.
同理可知,四边形CEGD是平行四边形,所以GE∥DC,同理证得GE∥平面BCD,因为AG,GE 平面AGE,且AG∩GE=G,BC,DC 平面BCD,BC∩DC=C,所以平面AGE∥平面BCD,因为AE 平面AGE,所以AE∥平面BCD.
(2)解 因为AF=2,DF=4,则DF2=AD2+AF2,故AD⊥AF,
又AB⊥AD,AF⊥AB,AD∩AF=A,所以AB⊥平面ADF.
连接DE,该几何体被分割为四棱锥D-ABEF和三棱锥D-BCE,
专题三 立体几何
上篇
内容索引
01
02
03
高考小题突破4 空间几何体的结构、表面积与体积
高考小题突破5 空间点、直线、平面的位置关系
培优拓展 巧设变量速求立体几何中的动态、最值问题
04
培优拓展 巧用公共点速定立体几何中的截面、交线问题
05
◎高考保分大题三 立体几何中的证明与计算
考情分析 1.题型、题量稳定:高考对该部分的考查一般为“2小1大”,分值约22分,多为中档题.
2.重点突出:
(1)客观题重点考查空间几何体的表面积与体积的求解、几何体中的线面关系等判断以及几何体与球的切、接等;
(2)主观题主要考查空间平行与垂直关系的证明、几何体体积、点到平面距离的求解为重点,多为中档解答题.
3.核心素养:直观想象、逻辑推理、数学运算.
备考策略 1.夯实基础:空间几何体的结构特征以及空间线面关系是立体几何的根本,平面图形中的平行与垂直关系是空间线面关系逻辑证明的起点、突破口.
2.掌握技巧:空间线面关系的证明,要熟练掌握相关定理,抓住平面图形的结构特征;体积与距离的求解,要注意灵活换底、分割法以及等积变换法.
3.强化转化:平面化思想是解决线面关系的基础,也是命题的重点;分割转化与等积转化是求解表面积、体积问题的重要思想.
真题感悟
1.(2021·全国甲·文7)在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥A-EFG后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是( )
正视图
答案 D
解析 由题意还原该正方体的直观图如图所示,该多面体的三视图中,相应的侧视图为D.
答案 C
解析 如图,甲、乙两个圆锥的侧面展开图刚好拼成一个圆,设圆的半径(即圆锥的母线长)为3,则圆的周长为6π,甲、乙两个圆锥的底面半径分别为r1,r2,高分别为h1,h2,则2πr1=4π,2πr2=2π,则r1=2,r2=1,由勾股定理得,
答案 C
解析 设等边三角形ABC的边长为a,球O的半径为R,△ABC的外接圆的半径
4.(2022·全国乙·文12)已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则当该四棱锥的体积最大时,其高为( )
答案 C
5.(2021·全国甲·文14)已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为 .
答案 39π
6.(2022·全国乙·文18)如图,四面体ABCD中,AD⊥CD,AD=CD,
∠ADB=∠BDC,E为AC的中点.
(1)证明:平面BED⊥平面ACD;
(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求三棱锥F-ABC的体积.
(1)证明 ∵AD=CD,∠ADB=∠BDC,BD=BD,∴△ABD≌△CBD.∴AB=BC.又E为AC的中点,∴BE⊥AC.∵AD=CD,且E为AC的中点,∴DE⊥AC.又DE∩BE=E,∴AC⊥平面BED.∵AC 平面ACD,∴平面BED⊥平面ACD.
(2)解 ∵AB=BC=2,∠ACB=60°,∴△ABC为等边三角形.
知识精要
1.空间几何体的表面积与体积
表面积=侧面积+底面积
误区警示
2.直线、平面平行的判定及其性质
(1)线面平行的判定定理:a α,b α,a∥b a∥α.
(2)线面平行的性质定理:a∥α,a β,α∩β=b a∥b.
(3)面面平行的判定定理:a β,b β,a∩b=P,a∥α,b∥α α∥β.
(4)面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b a∥b.
易漏掉线在面内这个条件
3.直线、平面垂直的判定及其性质
(1)线面垂直的判定定理:m α,n α,m∩n=P,l⊥m,l⊥n l⊥α.
(2)线面垂直的性质定理:a⊥α,b⊥α a∥b.
(3)面面垂直的判定定理:a β,a⊥α α⊥β.
(4)面面垂直的性质定理:α⊥β,α∩β=l,a α,a⊥l a⊥β.
漏掉此处条件,a⊥β还成立吗
误区警示
上述八个定理成立的条件,每一个条件都缺一不可.
4.空间中点到平面的距离的求法
(1)定义法:过点向平面作垂线,点与垂足的距离.
(2)“等积法”:求解点到平面的距离常转化为锥体的高,利用三棱锥体积公式求点到平面的距离.
转化与化归思想,“换底”是为了能求出体积,底面上的高能求出是关键
常用结论
高考小题突破4
考点一
空间几何体的三视图
典例突破1(1)(2022·浙江二模)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图是( )
(2)(2022·宁夏六盘山二模)如图,网格纸中小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体中最长的棱长为( )
答案 (1)C (2)C
解析 (1)将几何体各顶点字母标记如图,从左侧观察,得到如图所示的侧视图,其中,对角线DE被几何体左侧面遮挡,应当为虚线,故选C.
(2)该几何体为三棱锥A-BCD,三棱锥A-BCD是由以下四棱锥A-BCDE截去三棱锥A-BDE所剩下的部分,
由于AE=DE=BC=2,EB=DC=4,
解题技巧
解决三视图问题的解题思路
由直观图确 定三视图 (1)要根据三视图的含义及画法和摆放规则确认.
(2)要熟悉常见几何体的三视图
由三视图 还原到直 观图 (1)根据俯视图确定几何体的底面.
(2)根据正视图或侧视图确定几何体的侧棱与侧面的特征,调整实线和虚线所对应的棱、面的位置.
(3)确定几何体的直观图形状
对点练1(1)(2022·甘肃兰州模拟)如图所示,在网格上小正方形的边长为1,粗实线画出的是某多面体的三视图,若此多面体的所有顶点均可以放置在一个正方体的各面内,则此正方体的对角线长为( )
(2)在三棱锥P-ABC中,底面ABC是锐角三角形,PC垂直于平面ABC,若取垂直于平面PAC的方向为正视图的方向,其三视图中正视图和侧视图如图所示,则棱PB的长为 .
解析 (1)如图所示,由已知三视图可以看出,直观图中各个顶点在正方体的面的中心位置,其中AB为正视图中两个小正方形的边长,即AB=2,所以可以得到正方体的棱长为2,所以正方体的体对角线长为
(2)根据正视图可知,PC=4,B点在AC的投影位于AC的中点,不妨设其为H,可得AH=HC=2,
考点二
空间几何体的表面积和体积
考向1空间几何体的侧面积和表面积
典例突破2(1)(2022·安徽宣城二模)刘徽是我国古代杰出的数学家.他将底面是直角三角形的直三棱柱称为“堑堵”,将
底面为矩形且一条侧棱垂直于底面的四棱
锥称为“阳马”.已知某“堑堵”与某“阳马”组
合而成的几何体的三视图如图所示,则该
几何体的表面积是( )
(2)(2022·安徽巢湖一中模拟)已知某几何体的三视图如图所示,则该几何体的表面积为( )
A.168+6π B.132+6π
C.168+24π D.132+24π
答案 (1)B (2)A
解析 (1)由三视图还原几何体如图所示.
由题意易知,四边形ABED为正方形,四边形BCFE为矩形,且
(2) 由三视图知该几何体为长方体中去掉一个圆锥体,如图所示,
所以圆锥底面半径为3,母线长为5,侧面积为5×3×π=15π,底面积为9π,则几何体的表面积为2×6×6+4×6×4+15π-9π=168+6π.
故选A.
解题技巧
求几何体表面积的方法
基本思路 将立体几何问题转化为平面图形问题,即空间图形平面化
分割法 求不规则几何体的表面积时,通常将所给几何体分割成柱、锥、台体、球,先求这些柱、锥、台体、球的表面积,再通过求和或作差求得所给几何体的表面积
对点练2(1)(2022·黑龙江齐齐哈尔一模)如图所示,网格中小正方形的边长为1,粗线所画为一个几何体的三视图,则该几何体的表面积为( )
(2)(2022·江西临川一中模拟)将一个边长为4的正三角形以其中一边所在直线为旋转轴旋转一周,所得几何体的表面积为 .
(2) 如图所示,正三角形ABC绕边AB所在直线旋转一周,得到的几何体是两个同底等高的圆锥,
考向2空间几何体的体积
典例突破3(1)(2022·全国甲·文4)如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为( )
A.8 B.12 C.16 D.20
(2) (2022·山东潍坊模拟)某品牌暖水瓶的内胆规格如图所示,分为①②③④四个部分(水瓶内胆壁厚不计),它们分别为一个半球、一个大圆柱、一个圆台和一个小圆柱.若其中圆台部分的体积为
52π cm3,且水瓶灌满水后盖上瓶塞时水溢出
cm3,则盖上瓶塞后水瓶的最大盛水量为( )
答案 (1)B (2)A
解析 (1)该多面体的直观图如图所示,多面体是一个正方体和一个三棱柱
解题技巧
求空间几何体的体积的常用方法
公式法 对于规则的几何体的体积,可直接利用体积公式求解
等积法 等积法也称等积转化或等积变形,通过选择合适的底面来求几何体体积的一种方法,多用来解决锥体的体积,特别是三棱锥的体积
割补法 求不规则几何体的体积,常用分割或补形的思想,将不规则几何体转化为规则几何体,以易于求解
对点练3(1)(2022·陕西咸阳三模)计时沙漏制作简洁方便,也实用,该几何体是由简单几何体组合而成的封闭容器(内装一
定量的细沙),其三视图如图所示(沙漏尖端忽
略不计),则该几何体的体积为( )
(2)(2022·宁夏银川一中二模)如图所示的五面体ABCDEF,其中AB∥DC∥EF,AB=3,CD=2,EF=1,EF到平面ABCD的距离是2,AB与CD之间的距离是1,∠EAB,∠FBA,∠EDC,∠FCD均为锐角,则此五面体的体积为( )
A.2 B.3
答案 (1)A (2)A
(2) 如图,过点E作EQ⊥AB,EP⊥CD,垂足分别为Q,P.过点F作FN⊥AB,FM⊥CD,垂足分别为N,M.
连接PQ,MN.
则将几何体分为四棱锥E-AQPD,三棱柱EPQ-FMN,四棱锥F-BCMN三部分.
解析 (1)由三视图知几何体是由两个底面直径为2,高为2的圆锥组成,所以
考点三
球与几何体的切、接问题
考向1外接球
典例突破4(1)(2022·辽宁东北育才学校模拟)2020年迪拜世博会中国馆建筑外观模仿中国传统灯笼,寓意希望和光明.它的形状可视为内外两个同轴圆柱,某爱好者制作了一个中国馆的实心模型,已知模型内层底面圆的直径为12 cm,外层底面圆的直径为16 cm,且内外层圆柱的底面圆周都在一个直径为20 cm的球面上,则此模型的体积为( )
A.304π cm3 B.840π cm3
C.912π cm3 D.984π cm3
(2)(2022·新高考Ⅱ·7)已知正三棱台的高为1,上下底面的边长分别为
,其顶点都在同一球面上,则该球的表面积为( )
A.100π B.128π C.144π D.192π
答案 (1)C (2)A
(2)设外接球的半径为R,由题意得,上底面所在平面截球所得圆的半径是3,下底面所在平面截球所得圆的半径是4,
解题技巧
求多面体的外接球半径的技巧
解题依据 球的性质:任何直角所对的棱必然是球的直径
补形法 侧面为直角三角形,或正四面体,或对棱相等,或线面垂直的模型,可以还原到正方体或长方体模型中去求解
定义法 到各个顶点距离均相等的点为外接球的球心,方法是先确定有特殊底面的外接圆的圆心,再过圆心作垂直此面的垂线,则球心一定在此垂线上,最后根据其他顶点确定球心的准确位置,列关系式求解
对点练4(2022·云南二模)三棱锥P-ABC的顶点都在以PC为直径的球M的球面上,PA⊥BC.若球M的表面积为100π,PA=8,则三棱锥P-ABC的体积的最大值为( )
答案 A
解析 因为三棱锥P-ABC的顶点都在以PC为直径的球M的球面上,所以PA⊥AC,PB⊥BC,又PA⊥BC,AC∩BC=C,故PA⊥平面ABC.
因为PA∩PB=P,故BC⊥平面PAB,又AB 平面PAB,故BC⊥AB.
因为球M的表面积为100π,设球的半径为R,则4πR2=100π,解得R=5,即PC=10,
考向2内切球
典例突破5 粽子古称“角黍”,是中国传统的节庆食品,由粽叶包裹糯米等食材蒸制而成.因各地风俗不同,粽子的形状和味道也不同,某地流行的“五角粽子”,其形状可以看作所有棱长均为4 cm的正四棱锥,现在需要在粽子内部放入一颗咸蛋黄,蛋黄的形状近似地看成球,则当这个蛋黄的体积最大时,蛋黄的半径为( )
答案 B
解题技巧
解决内切问题的思路
基本步骤 (1)抓切点:要认真分析图形,明确切点的位置;
(2)做截面:作出合适的截面图;
(3)定关系:确定有关元素间的数量关系
组合体 问题 (1)球与旋转体的组合,通常作它们的轴截面解题;
(2)球与多面体的组合,通过多面体的一条侧棱和球心(或“切点”
“接点”)作出截面图
对点练5(2022·辽宁沈阳二模)现有一个侧面展开图为半圆形的圆锥,其内部放有一个小球,当小球体积最大时,该圆锥与小球的体积之比是( )
A.9∶4 B.9∶5 C.3∶2 D.3∶1
答案 A
解析 由圆锥侧面展开图为半圆,设圆锥母线为l,底面半径为R,则2πR=πl,所以l=2R,可知圆锥轴截面为正三角形,圆锥高为 R ,
又由当小球是圆锥的内切球时,小球体积最大,轴截面如图所示:设此时小球半径为r,
高考小题突破5
考点
空间直线、平面位置关系的判断
典例突破(1)(2022·山西临汾三模)已知m,n是两条不同的直线,α,β,γ是三个不同的平面,下列命题中正确的是( )
A.若α⊥β,β⊥γ,则α⊥γ
B.若m⊥α,n⊥α,则m∥n
C.若α⊥β,m α,n β,则m⊥n
D.若m∥α,n∥α,则m∥n
(2)(2020·全国Ⅱ·文16)设有下列四个命题:
p1:两两相交且不过同一点的三条直线必在同一平面内.
p2:过空间中任意三点有且仅有一个平面.
p3:若空间两条直线不相交,则这两条直线平行.
p4:若直线l 平面α,直线m⊥平面α,则m⊥l.
则下述命题中所有真命题的序号是 .
①p1∧p4 ②p1∧p2 ③( p2)∨p3
④( p3)∨( p4)
答案 (1)B (2)①③④
解析 (1)若α⊥β,β⊥γ,则α,γ可以平行、相交,故A错误;若m⊥α,n⊥α,则m∥n,故B正确;由α⊥β,m α,n β推不出m⊥n,故C错误;若m∥α,n∥α,则m,n可以平行、相交、异面,故D错误.故选B.
(2)∵p1,p4为真命题,p2,p3为假命题,∴ p2, p3为真命题,∴p1∧p4为真命题,p1∧p2为假命题,( p2)∨p3为真命题,( p3)∨( p4)为真命题.故填①③④.
解题技巧
判断空间位置关系的三种方法
定理法 借助空间直线、平面平行与垂直的判定定理和性质定理进行逻辑推理判断
反证法 当从正面入手较难时,可用反证法,推出与题设或公认的结论相矛盾的命题,进而做出判断
模型法 借助空间几何体模型,如借助长方体、正四面体等几何体模型观察线面关系,结合有关定理进行肯定或否定
对点练(1)(2022·黑龙江齐齐哈尔二模)如图是一个正方体的平面展开图,则在正方体中直线AB与CD的位置关系为( )
A.相交
B.平行
C.异面并且垂直
D.异面但不垂直
(2)(2022·陕西咸阳三模)已知直线m和平面α,β满足m⊥α,α⊥β,则( )
A.m⊥β B.m∥β或m β
C.m β D.m∥β
答案 (1)D (2)B
解析 (1) 将展开图还原成正方体,由图可知,直线AB与CD的位置关系是异面.连接CE,则CE∥AB,∠DCE或其补角即为直线AB与CD的夹角,又∠DCE=60°,所以直线AB与CD不垂直.故选D.
(2)由m⊥α,α⊥β,若m β,则m∥β,否则m β,所以m∥β或m β.故选B.
培优拓展
巧设变量速求立体几何中的动态、最值问题
立体几何中的“动态问题”是指空间中的某些点、线、面的位置是不确定的或可变的一类开放性问题,解决这类问题应该动静结合、化动为静,找到相应的几何关系,对于探究存在问题或动态范围(最值)问题,用定性分析比较难或繁时,可以引进参数,把动态问题划归为静态问题.具体地,可通过构建方程、函数或不等式等进行定量计算,以算促证.
问题提出
具体可以有以下几种解决方法:
(1)函数法:某些点、线、面的运动,必然导致某些位置关系或一些变量的变化.变量变化时会引发其他变量的变化,从而建立函数关系,将立体几何问题转化为函数问题来解决.
(2)等价转换法:动和静是相对的,在运动变化过程中,要善于寻找或构造与之相关的一些不变因素,将一些变化的点、线、面进行合理转换,实现变量与不变量的结合.
【例1】 (2022·贵州模拟)设矩形ABCD(AB>BC)的周长为20,把△ABC沿AC向△ADC折叠,AB折叠后交DC于点P,点B落在点E处,则线段AP的长度最小值为( )
结论应用
答案 D
解析 ∵四边形ABCD是矩形,且△ABC沿AC向△ADC折叠,
∴AD=EC,∠ADP=∠CEP=90°,∠APD=∠CPE,
∴△ADP≌△CEP,∴AP=CP.
设AB=x,DP=y,∴AP=CP=x-y.又∵矩形ABCD(AB>BC)的周长为20,
∴AD=10-x.
由勾股定理,可得(10-x)2+y2=(x-y)2,
∵AB>BC,∴0<10-x
【例2】 如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,点P为线段AD1上的动点,点Q为线段B1C上的动点,则PQ长度的最小值为 .
答案 1
解析 (方法一)设P点在平面BCC1B1上的射影为H,则PH⊥QH.由题意可知PH=1.
显然当x=0,即点Q,H重合,也就是PQ⊥平面BCC1B1时,PQ取得最小值1.
(方法二)因为ABCD-A1B1C1D1是正方体,所以平面AA1D1D∥平面BB1C1C,平面AA1D1D与平面BB1C1C的距离是1,因为异面直线AD1与B1C的距离是平面AA1D1D与平面BB1C1C的距离,PQ长度的最小值是AD1与B1C的距离,是1.
评析 该题虽然有两个动点,通过平面的垂线化归到直角三角形中的线段长度,从而只需要设置一个变量即可.我们也可以根据几何体的结构特征,将问题转化为两个平面之间的距离求解.
【例3】 如图1,在矩形ABCD中,AB=3,AD=1,E为CD的中点,F为线段CE(除端点外)上的动点,如图2,将△AFD沿AF折起,点D落在点D1的位置,使平面ABD1⊥平面ABC,在平面ABD1内,过点D1作D1K⊥AB,K为垂足,则AK长度的取值范围为( )
图1
图2
答案 A
解析 过点F作FM⊥AB交AB于点M,连接FK,
设AK=t,FC=x,0
在Rt△FMK中,FK2=1+(3-t-x)2,D1F=3-x,
在Rt△D1FK中,FK2+D1K2=D1F2,∴1-t2+1+(3-t-x)2=(3-x)2,化简得1-3t+tx=0,
【例4】如图所示,已知四棱锥S-ABCD的底面是边长为6的菱形,
∠BAD=60°,AC,BD相交于点O,SO⊥平面ABCD,SO=4,E是BC的中点,动点P在该棱锥表面上运动,并且总保持PE⊥AC,则动点P的轨迹的长为( )
A.3 B.7 C.13 D.8
答案 D
解析 取DC,SC的中点G,F,连接GE,FE,FG.∵E是BC的中点,
∴GE∥DB,FE∥SB,显然GE∥平面SBD,FE∥平面SBD.
又GE,FE 平面EFG,GE∩FE=E,∴平面EFG∥平面SBD.
∵SO⊥平面ABCD,AC 平面ABCD,∴SO⊥AC.
又四边形ABCD是菱形,∴DB⊥AC.
∵SO∩DB=O,∴AC⊥平面SBD,则AC⊥平面EFG,
故只要动点P在平面EFG内,即总保持PE⊥AC.
又动点P在棱锥表面上运动,∴动点P的轨迹的长即为△EFG的周长.
∵四边形ABCD为菱形,边长为6,且∠BAD=60°,
∴BD=6,则OB=OD=3.又SO=4,∴SB=SD=5,
故FE=FG= ,GE=3,∴△EFG的周长为8.故选D.
评析 确定点P的轨迹,就是把已知条件“PE⊥AC”转化为过点E与直线AC垂直的平面与棱锥表面的交线,进而确定轨迹的形状进行求解.探寻变化过程中的不变关系,是解决动态问题的常用手段.对于翻折或投影问题,若能抓住相关线或面的垂面,化空间为平面,则容易找到问题的核心.
培优拓展
巧用公共点速定立体几何中的截面、交线问题
在处理空间几何问题时,常遇到用一个平面去截几何体,判断截面的形状或求截面的周长、面积等问题.很多同学空间想象力不强,确定平面的公理运用不够熟练,遇到此类问题往往束手无策,为此,有必要总结一下画截面的方法,帮助学生又快又准地找出截面,顺利解决截面问题.
画一个平面截多面体的截面,关键是确定交线,常用的方法有:
方法1.直接连接法:当有两点在几何体的同一个面上时,连接该两点即为几何体与截面的交线.
问题提出
方法2.作平行线法:过直线与直线外一点作截面,常用到面面平行、线面平行的性质,通过该点找直线的平行线,即找到几何体与截面的交线.
方法3.作延长线找交点法:观察在同一个平面上的两点,连接并延长至另一个点所在平面,同一个平面有两点则可连线,需要注意长度的运算、比例关系,否则难以确定位置关系.
名师点析
确定截面的主要依据有:(1)平面的四个公理及推论;(2)直线和平面平行的判定和性质;(3)两个平面平行的性质;(4)球的截面的性质.
【例1】 (2022·山东临沂一模)已知正三棱台ABC-A1B1C1的上下底面边长分别为2和5,侧棱长为3,则以下底面的一个顶点为球心,半径为2的球面与此正三棱台的表面的交线长为 .
答案 2π
解析不妨设以下底面的顶点A为球心作球面.
由题意,得△ABC是边长为5的等边三角形,正三棱台的侧面均为全等的等腰梯形,如图所示,在四边形ABB1A1中,AB=5,A1B1=2,AA1=BB1=3,
结论应用
在棱AB上取BF=2,连接A1F,易知△AA1F为等边三角形,即∠A1AB=60°.同理,∠A1AC=60°.则以下底面的顶点A为球心,半径为2的球面与此正三棱台
评析 该题是球面与棱台表面的交线,需要将其转化为球的截面的性质,每段弧线的圆心角就是正三棱台侧面等腰梯形的底角或下底面正三角形的内角,所以问题的关键就是求出该扇形的圆心角.
答案 A
解析 由正四面体的棱长为2 可求得它的外接球半径是3,因为3> ,所以正四面体的一个平面与球相交的截面如图所示,△BMN是正四面体的一个面,点O1是正四面体一个平面截球面所得截面圆的圆心.O1D⊥BM,点A是BM与圆O1的交点.
则正四面体表面与球面的交线的总长度为π×4=4π.
评析 该题是球面与棱锥表面的交线,需要将其转化为球的截面的性质,问题的关键就是准确求出截面圆的半径,然后利用弧长公式和几何体的对称性求得最后结果.
【例3】 如图,在正方体ABCD-A1B1C1D1中,点E,F分别是棱B1B,B1C1的中点,点G是棱C1C的中点,则过线段AG且平行于平面A1EF的截面图形为( )
A.矩形 B.三角形
C.正方形 D.等腰梯形
答案 D
解析 取BC的中点H,连接AH,GH,由题意得GH∥EF,AH∥A1F,又GH 平面A1EF,EF 平面A1EF,∴GH∥平面A1EF,同理AH∥平面A1EF,又GH∩AH=H,GH,AH 平面AHG,∴平面AHG∥平面A1EF,连接AD1,D1G,则AD1∥GH,又A∈平面AHG,GH 平面AHG,∴AD1 平面AHG,即点A,H,G,D1确定一个平面,故过线段AG且与平面A1EF平行的截面图形为四边形AHGD1,显然为等腰梯形.
评析 该题是平面与几何体的截面问题,确定该截面与几何体各棱的交点是确定截面形状的关键.
【例4】如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,点M,N分别是A1D1,A1B1的中点,过直线BD的平面α∥平面AMN,则平面α截该正方体所得截面的面积为( )
答案 B
解析 如图所示,取B1C1的中点E,C1D1的中点F,连接EF,BE,DF,B1D1,则EF∥B1D1,B1D1∥BD,所以EF∥BD,故EF,BD在同一平面内,
连接ME,因为M,E分别为A1D1,B1C1的中点,所以ME∥AB,且ME=AB,
所以四边形ABEM是平行四边形,所以AM∥BE,
又因为BE 平面BDFE,AM 平面BDFE,
所以AM∥平面BDFE,同理AN∥平面BDFE,
因为AM∩AN=A,AM,AN 平面AMN,
所以平面AMN∥平面BDFE,即等腰梯形BDFE就是所求的截面.
评析 根据面面平行的判定定理,准确确定平面α的位置,进而确定交线,确定截面的形状,即可将问题转化为平面图形中的计算问题.
【例5】 已知四棱柱ABCD-A1B1C1D1的底面为菱形,AA1⊥底面ABCD,
AA1=6,AB=8,∠BCD=60°,点M是线段BC上靠近C的四等分点,动点N在四棱柱ABCD-A1B1C1D1的表面,且MN⊥BD1,则动点N的轨迹长度为 .
解析 因为四棱柱ABCD-A1B1C1D1的底面为菱形,AA1⊥底面ABCD,所以BB1⊥AC,BD⊥AC,又因为BB1∩BD=B,所以AC⊥平面BDD1B1,所以BD1⊥AC,故在AB上取点F,使得BF=3FA,连接MF,则MF∥AC,BD1⊥MF.
在BB1上取点G,使得BG=2GB1,
设MF与BD的交点为O,连接GO,
在△D1DB中,DD1=6,BD=8,DD1⊥BD,
所以△D1DB∽△OBG,故∠D1BD=∠OGB,
所以BD1⊥OG,又BD1⊥MF,OG∩MF=O,OG,MF 平面MFG,所以BD1⊥平面MFG.
故△MFG的边即为点N的轨迹.
高考保分大题三
考点一
证明平行关系与求几何体的体积
典例突破1(2022·全国甲·文19)小明同学参加综合实践活动,设计了一个封闭的包装盒.包装盒如图所示:底面ABCD是边长为8(单位:cm)的正方形,△EAB,△FBC,△GCD,△HDA均为正三角形,且它们所在的平面都与平面ABCD垂直.
(1)证明:EF∥平面ABCD;
(2)求该包装盒的容积(不计包装盒材料的厚度).
(1)证明 过点E作EE'⊥AB于点E',过点F作FF'⊥BC于点F',连接E'F'.
∵底面ABCD是边长为8的正方形,△EAB,△FBC均为正三角形,且它们所在的平面都与平面ABCD垂直,∴EE'⊥平面ABCD,FF'⊥平面ABCD,且EE'=FF',∴四边形EE'F'F是平行四边形,则EF∥E'F'.
∵E'F' 平面ABCD,EF 平面ABCD,
∴EF∥平面ABCD.
(2)解 过点G,H分别作GG'⊥CD,HH'⊥DA,交CD,DA于点G',H',连接F'G',
G'H',H'E',AC.
由(1)及题意可知,G',H'分别为CD,DA的中点,EFGH-E'F'G'H'为长方体,故该包装盒由一个长方体和四个相等的四棱锥组合而成.∵底面ABCD是边长为
规律方法
证明线面平行与求几何体体积的解题思路
(1)证明线面平行,一般利用线面平行的判定定理,难点是找直线在平面内的平行线:
①利用三角形的中位线找平行线证明线面平行;
②构造平行四边形,找平行线;
③利用平行线分线段成比例定理推论的逆定理证明线线平行.
(2)求几何体的体积,一般思路是围绕已知条件和要求的几何体的底和高,通过几何体的几何性质,建立已知和未知的关系,依据题意可借助方程的思想求出未知数,从而求出体积.对于三棱锥的体积,常利用等体积法进行转换.
对点练1(2022·陕西榆林三模)如图,在多面体ABCDEF中,底面ABCD是正方形,AF∥DE,AF=AD=2DE,AF⊥底面ABCD.
(1)证明:BD∥平面CEF;
(2)若AF=4,求该多面体的体积.
(1)证明 如图所示,
连接AC,交BD于点M,取CF的中点N,连接MN,NE.
因为四边形ABCD是正方形,所以点M是AC的中点,所以MN∥AF,MN= AF.
又AF∥DE,AF=2DE,所以MN∥DE,MN=DE,
故四边形MNED是平行四边形,则BD∥NE.
又BD 平面CEF,NE 平面CEF,所以BD∥平面CEF.
(2)解 设该多面体的体积为V,则V=V三棱锥C-ABF+V四棱锥C-ADEF.
因为AF⊥底面ABCD,所以AF⊥BC,
又AB⊥BC,AF∩AB=A,所以BC⊥平面ABF,同理可得CD⊥平面ADEF.因为
对点练2(2022·河南洛阳一模)已知底面为菱形的四棱锥P-ABCD中,△PAD是等边三角形,平面PAD⊥平面ABCD,E,F分别是棱PC,AB上的点.
(1)从下面①②③中选取两个作为条件,证明另一个成立.
①F是AB的中点;②E是PC的中点;③BE∥平面PDF.(只需选择一种组合进行解答即可)
(2)若AD=2,∠DAB=60°,PE=EC,求三棱锥P-BDE的体积.
解 (1)①② ③.
因为F是AB的中点,E是PC的中点,取PD的中点M,连接ME,MF,则ME∥CD,且ME= CD,又四边形ABCD为菱形,所以BF∥CD且BF= CD,所以BF∥ME且BF=ME,所以四边形BEMF为平行四边形,所以BE∥FM,又BE 平面PDF,FM 平面PDF,所以BE∥平面PDF.
②③ ①.
取PD的中点M,连接ME,MF,因为E是PC的中点,
所以ME∥CD,且ME= CD,又BF∥CD,
所以BF∥ME,
因为BE∥平面PDF,平面BEMF∩平面PDF=MF,BE 平面BEMF,所以BE∥MF,所以四边形BEMF为平行四边形,所以BF=ME,即BF= CD= AB,所以F是AB的中点.
①③ ②.
取DC的中点N,连接NB,NE,
因为F是AB的中点,所以BF∥DN且BF=DN,
所以四边形BNDF为平行四边形,所以BN∥DF,
因为BN 平面PDF,DF 平面PDF,所以BN∥平面PDF,
又BE∥平面PDF,BE∩BN=B,BE,BN 平面BEN,所以平面PDF∥平面BEN.
因为平面BEN∩平面PCD=EN,平面PDF∩平面PCD=PD,所以EN∥PD,所以E是PC的中点.
(2)取AD的中点G,连接PG,
因为△APD为等边三角形,所以PG⊥AD,又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,所以PG⊥平面ABCD,又AB=BC=CD=AD=PA=PD=2,
考点二
证明垂直关系与求几何体的体积
典例突破2(2022·宁夏石嘴山一模)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AB=PA=1,AD=2,点F是PB的中点,点E为BC上的一点.
(1)求证:AF⊥平面PBC;
(2)若三棱锥P-DEF的体积为 ,求CE的长.
(1)证明 因为四边形ABCD为矩形,所以BC⊥AB,
又因为PA⊥平面ABCD,所以PA⊥BC,因为AB 平面PAB,PA 平面PAB,PA∩AB=A,所以BC⊥平面PAB,又因为AF 平面PAB,所以BC⊥AF.又因为PA=AB,F是PB的中点,所以AF⊥PB,因为PB 平面PBC,BC 平面PBC,PB∩BC=B,所以AF⊥平面PBC.
(2)解 因为AB=PA=1,
设BE=x,
疑难突破
证明线面垂直或面面垂直,一般都会要证明线线垂直,其方法有:
(1)通过计算,运用勾股定理寻求线线垂直;
(2)利用面面垂直寻求线面垂直,从而得到线线垂直;
(3)应用等腰(等边)三角形三线合一性质,即三角形底边的中线同时是高和角平分线,得到线线垂直;
(4)应用两条平行线的性质,有一条与一个平面中的直线垂直,则另一条也与平面中的直线垂直.
对点练3(2022·四川泸州三模)已知直三棱柱ABC-A1B1C1中,D为B1C1的中点.
(1)若AB=AC=2,BC=2 ,AA1=2,求点C到平面ABD的距离;
(2)从下面①②③中选取两个作为条件,证明另外一个成立.
①A1B⊥B1C;②BD⊥B1C;③A1B1=A1C1.
解 (1)因为AB=AC=2,BC=2 ,
所以AB2+AC2=BC2,即△ABC是等腰直角三角形,AB⊥AC,所以
S△ABC= ×2×2=2.
因为该三棱柱是直棱柱,所以AA1⊥平面A1B1C1.
连接A1D,A1D 平面A1B1C1,所以AA1⊥A1D.
(2)选择①②为条件,证明③成立.
证明:连接A1D,
因为A1B⊥B1C,BD⊥B1C,A1B∩BD=B,A1B 平面A1BD,BD 平面A1BD,所以B1C⊥平面A1BD.
因为A1D 平面A1BD,所以B1C⊥A1D.
又该三棱柱是直棱柱,所以BB1⊥平面A1B1C1.
因为A1D 平面A1B1C1,所以BB1⊥A1D.
因为BB1∩B1C=B1,BB1 平面BCC1B1,B1C 平面BCC1B1,所以A1D⊥平面BCC1B1.
因为B1C1 平面BCC1B1,所以A1D⊥B1C1.
因为D为B1C1的中点,所以A1B1=A1C1.
选择①③为条件,证明②成立.
证明:连接A1D,因为A1B1=A1C1,D为B1C1的中点,所以A1D⊥B1C1.
因为该三棱柱是直棱柱,所以BB1⊥平面A1B1C1.
因为A1D 平面A1B1C1,所以BB1⊥A1D.
因为BB1∩B1C1=B1,BB1 平面BCC1B1,B1C1 平面BCC1B1,所以A1D⊥平面BCC1B1.
因为B1C 平面BCC1B1,所以A1D⊥B1C.又A1B⊥B1C,A1B∩A1D=A1,A1B 平面A1BD,A1D 平面A1BD,所以B1C⊥平面A1BD,因为BD 平面A1BD.所以BD⊥B1C.
选择②③为条件,证明①成立.
证明:连接A1D,因为A1B1=A1C1,D为B1C1的中点,所以A1D⊥B1C1.
因为该三棱柱是直棱柱,所以BB1⊥平面A1B1C1.
因为A1D 平面A1B1C1,所以BB1⊥A1D.
因为BB1∩B1C1=B1,BB1 平面BCC1B1,B1C1 平面BCC1B1,所以A1D⊥平面BCC1B1.
因为B1C 平面BCC1B1,所以A1D⊥B1C.
又BD⊥B1C,BD∩A1D=D,BD 平面A1BD,A1D 平面A1BD,所以B1C⊥平面A1BD.
因为A1B 平面A1BD,所以A1B⊥B1C.
对点练4(2021·全国乙·文18)如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM.
(1)证明:平面PAM⊥平面PBD;
(2)若PD=DC=1,求四棱锥P-ABCD的体积.
(1)证明 ∵PD⊥平面ABCD,AM 平面ABCD,
∴PD⊥AM.
又PB⊥AM,PB∩PD=P,PB 平面PBD,PD 平面PBD,∴AM⊥平面PBD.
∵AM 平面PAM,∴平面PAM⊥平面PBD.
(2)解 ∵M为BC的中点,四边形ABCD为矩形,
∵AM⊥平面PBD,BD 平面PBD,
∴AM⊥BD,则有∠MAD+∠ADB=90°,又∠BAM+∠MAD=90°,
∴∠BAM=∠ADB,又∠DAB=∠ABM=90°,
考点三
空间位置关系的证明与求点面距
典例突破3(12分)(2022·内蒙古呼和浩特·一模)如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,PA=AB=2CD=2,∠ADC=90°,点E,F分别为PB,AB的中点.
(1)求证:CE∥平面PAD;
(2)求点B到平面PCF的距离.
【评分标准—找回丢分】
【教师讲评—触类旁通】
分析1:(1)问证明CE∥平面PAD,最基本的思路就是转化,既可以在平面PAD内找出与直线CE平行的直线;也可以说明过直线CE的一个平面与平面PAD平行;无论哪种思路,都要从平面图形中的平行关系入手;
分析2:(2)问中求点B到平面PCF的距离,显然直接作出垂线段不好处理,所以借助四面体BPCF的多变性——通过变换顶点、换底面求出其体积,利用体积相等列方程求解.体现了用数字刻画几何体特征的目的,也是方程思想的应用.
规律方法
求点A到平面α的距离的方法
直接法 通过线面垂直的证明,找到点A在平面α内的投影点A',则AA'的长即为点A到平面α的距离
等积变换法 通过转换棱锥的顶点棱锥的体积不变,表示出不同顶点下棱锥的高和底面积,再根据体积相等即可求出点到面的距离
对点练5如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
(1)证明 连接B1C,ME.
因为M,E分别为BB1,BC的中点,
因此四边形MNDE为平行四边形,MN∥ED.
又MN 平面C1DE,
所以MN∥平面C1DE.
(2)解 过C作C1E的垂线,垂足为H.由已知可得DE⊥BC,DE⊥C1C,所以DE⊥平面C1CE,故DE⊥CH.从而CH⊥平面C1DE,故CH的长即为C到平面C1DE的距离.由已知可得CE=1,C1C=4,
对点练6(2022·山西吕梁一模)在直四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,AB=2,AA1=4,点E,M,N分别是C1D1,AB1,CC1的中点.
(1)求证:MN∥平面A1EA;
(2)求点N到平面A1EA的距离.
(1)证明 取A1B1的中点P,连接MP,PC1,
因为PM平行且等于C1N,所以四边形PMNC1是平行四边形.
因为点E,P都是所在边的中点,所以A1P平行且等于EC1,
所以四边形A1PC1E是平行四边形,
所以PC1∥A1E,又PC1 平面A1EA,A1E 平面A1EA,
所以PC1∥平面A1EA.
又因为P,M是所在边的中点,所以PM∥AA1,又PM 平面A1EA,AA1 平面A1EA,所以PM∥平面A1EA.
而PC1∩PM=P,且PM,PC1均在平面PMNC1中,所以平面PMNC1∥平面A1EA.
又因为MN 平面PMNC1,所以MN∥平面A1EA.
(2)解 因为MN∥平面A1EA,所以点N到平面A1EA的距离等于点M到平面A1EA的距离,因为AB=C1D1=A1D1=2,AA1=4,而E为C1D1的中点,故ED1=1,所
考点四
翻折问题
典例突破4(2022·安徽芜湖一中三模)如图所示,在矩形ATCD中,AD=8,DC=3,B为TC的中点,△TAB沿AB翻折,使得点T到达点P的位置.连接PD,PC,得到四棱锥P-ABCD,点M为PD的中点.
(1)求线段CM的长度;
(2)若平面PAD⊥平面ABCD,求三棱锥P-ABD的体积.
(2) 取AD的中点O,连接BO,PO,则BO⊥AD,又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,所以BO⊥平面PAD,则BO⊥OP,
误区警示
翻折问题中的误区
平面图形翻折后成为空间图形,翻折后还在同一个平面上的线线关系不发生变化,不在同一个平面上的可能发生变化.解决这类问题就是要根据这些变与不变,去研究翻折以后的空间图形中的线面关系和各类几何量的度量值.
对点练7(2022·四川攀枝花二模)如图1,在直角梯形ABCD中,AD∥BC,AB⊥AD,点E为BC的中点,点F在AD上,EF∥AB,BC=EF=DF=4,将四边形CDFE沿EF边折起,如图2.
(1)证明:图2中的AE∥平面BCD;
(2)在图2中,若AD=2 ,求该几何体的体积.
图1
图2
(1)证明 取DF的中点G,连接AG,EG,CG.因为CE∥GF,CE=GF,所以四边形CEFG是平行四边形,所以CG∥EF∥AB且CG=EF=AB,
所以四边形ABCG是平行四边形,所以AG∥BC.因为AG 平面BCD,且BC 平面BCD,所以AG∥平面BCD.
同理可知,四边形CEGD是平行四边形,所以GE∥DC,同理证得GE∥平面BCD,因为AG,GE 平面AGE,且AG∩GE=G,BC,DC 平面BCD,BC∩DC=C,所以平面AGE∥平面BCD,因为AE 平面AGE,所以AE∥平面BCD.
(2)解 因为AF=2,DF=4,则DF2=AD2+AF2,故AD⊥AF,
又AB⊥AD,AF⊥AB,AD∩AF=A,所以AB⊥平面ADF.
连接DE,该几何体被分割为四棱锥D-ABEF和三棱锥D-BCE,
同课章节目录
