2023届高考二轮总复习课件(适用于老高考旧教材) 数学(文)专题一 三角函数与解三角形 课件(共162张PPT)
文档属性
| 名称 | 2023届高考二轮总复习课件(适用于老高考旧教材) 数学(文)专题一 三角函数与解三角形 课件(共162张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 17:33:14 | ||
图片预览





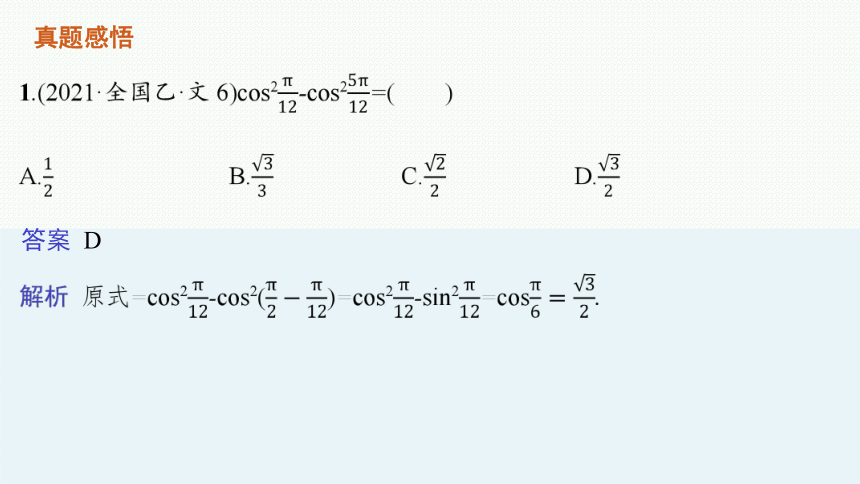



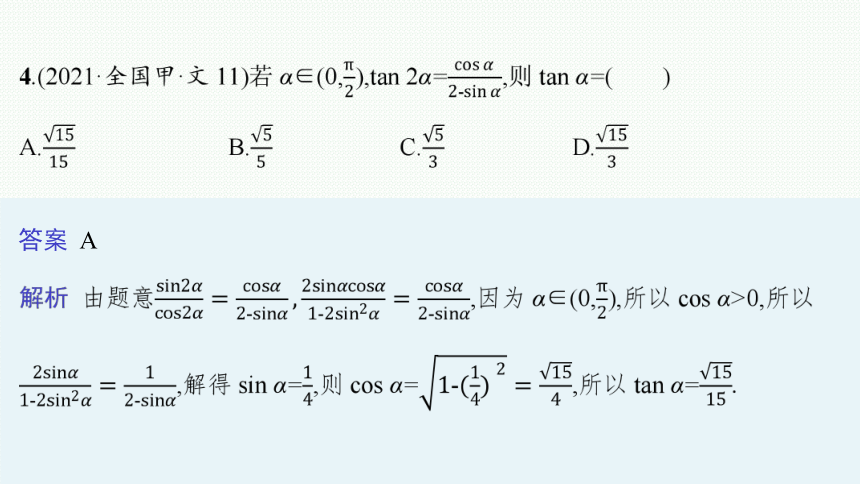

文档简介
(共162张PPT)
专题一 三角函数与解三角形
上篇
内容索引
01
02
03
高考小题突破1 三角函数的图象与性质
高考小题突破2 三角变换与解三角形
培优拓展 三角变换与解三角形中的变“角、名、式”
04
◎高考满分大题一 三角函数与解三角形
考情分析 三角函数与解三角形是高考的考点题型,从近五年的高考试题来看,呈现较强的规律性,每年的题量和分值一般是三个小题共15分或一个小题加一个大题共17分,两种情况间隔出现.该部分常考查的内容有三角函数的图象与性质,三角恒等变换与诱导公式,利用正弦定理和余弦定理解三角形.在解题过程中,要注意三角恒等变换公式的多样性和灵活性,注意题目中隐含的各种限制条件,选择合理的方法解题.
备考策略 1.让学生牢记公式概念,夯实基础.三角题几乎都要用到各类公式,牢记公式是进行运算的基础.看似简单,但是总有学生因公式应用错误而丢分,所以教学中要勤督促、多提问、常反复、多检查.
2.对于各类问题多整理,特点要记清,方法要用对.例如f(x)=Asin(ωx+φ)从整体考虑易于求单调区间、值域等,但有些函数化不成这种形式,如求f(x)=2sin x+sin 2x的值域,要用研究其他函数的方法去研究,必要时要用导数解决.还有在解三角形中,边化角、角化边都存在选择恰当的解题方向问题.
备考策略 3.注意细节,杜绝失误.三角问题虽然整体难度不大,但是细小问题较多,容易失误.例如:图象变换中的平移变换,先看函数名称是否相同,再看自变量系数,再确定平移方向及单位;再如三角求值问题中角的范围的考查等.
4.重视数学思想方法的应用.三角中常用的数学思想一是转化与化归思想:在三角恒等变换,利用正、余弦定理进行边角转化中应用广泛;二是数形结合思想:在求三角函数的最值(值域)及三角函数零点问题,方程或不等式问题时,要强化数形结合思想的应用.
真题感悟
答案 D
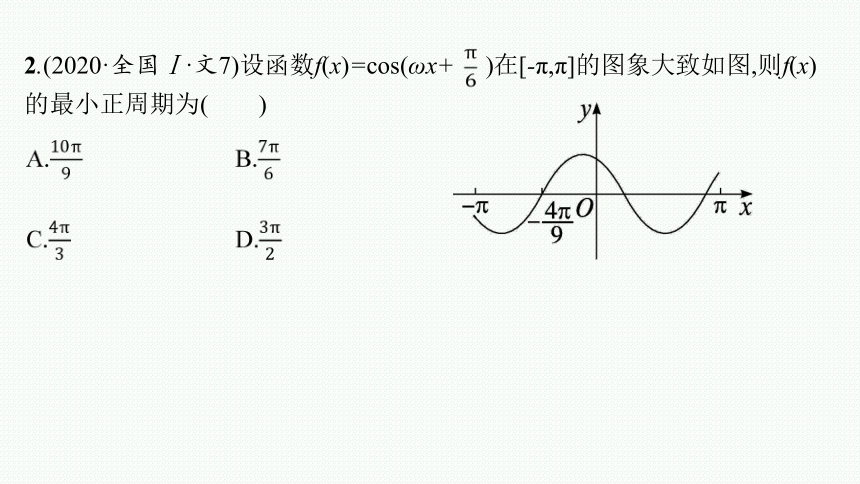
2.(2020·全国Ⅰ·文7)设函数f(x)=cos(ωx+ )在[-π,π]的图象大致如图,则f(x)的最小正周期为( )
答案 C
答案 D
解析 设BC=x,由余弦定理得19=4+x2-2×2x·cos 120°,解得x=3或x=-5(舍).故选D.
答案 A
5.(2021·全国乙·文15)记△ABC的内角A,B,C的对边分别为a,b,c,面积为 ,B=60°,a2+c2=3ac,则b= .
6.(2021·全国甲·文15)已知函数f(x)=2cos(ωx+φ)的部分图象如图所示,则
f( )= .
7.(2022·全国乙·文17)记△ABC的内角A,B,C的对边分别为a,b,c,已知
sin Csin(A-B)=sin Bsin(C-A).
(1)若A=2B,求C;
(2)证明:2a2=b2+c2.
(1)解 ∵sin Csin(A-B)=sin Bsin(C-A),A=2B,
∴sin Csin B=sin Bsin(C-A).
又sin B>0,∴sin C=sin(C-A).
(2)证明 (方法一)∵sin Csin(A-B)=sin Bsin(C-A),
∴sin C(sin A·cos B-cos Asin B)=sin B(sin Ccos A-cos Csin A),
即sin C·sin Acos B-sin Ccos Asin B=sin Bsin Ccos A-sin Bcos Csin A,
即sin A(sin Ccos B+cos Csin B)=2sin Bsin Ccos A,
即sin Asin(B+C)=2sin Bsin Ccos A,
即sin2A=2sin Bsin Ccos A.
即a2=b2+c2-a2,故2a2=b2+c2.
(方法二)∵sin Csin(A-B)=sin Bsin(C-A),∴sin Csin A·cos B-sin Csin Bcos A
=sin Bsin Ccos A-sin Bsin Acos C,
知识精要
1.三角函数的定义
名师点析
若|OP|=1,则sin α=y,cos α=x.若α∈(0, ),则sin α<α2.同角三角函数的基本关系
名师点析
(1)平方关系经常被逆用,即“1”的代换;
(2)商数关系也经常被逆用,即“切化弦”.
3.三角函数的图象与性质
知识点 内容
三角函数的图象与性质 (1)y=sin x图象的对称轴方程为x= +kπ,k∈Z,对称中心为(kπ,0),k∈Z;
图象与x轴的交点
y=cos x图象的对称轴方程为x=kπ,k∈Z,对称中心为
( +kπ,0),k∈Z
对称轴过图象的最高点或最低点
名师点析
正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个最小正周期.
4.两角和与差的正弦、余弦、正切公式
知识点 内容
两角和与差的正弦、余弦、正切公式 sin(α±β)=sin αcos β±cos αsin β;
cos(α±β)=cos αcos β sin αsin β;
tan(α±β)=
名师点析
两角和与差的正切公式的常用变式:tan α±tan β=(1 tan αtan β)tan(α±β).
5.二倍角公式及降幂公式
名师点析
由降幂公式开方并作角的代换得半角公式:
6.正弦、余弦定理
名师点析
三角形的三个常用结论
(1)tan A+tan B+tan C=tan A·tan B·tan C.
(2)A>B a>b sin A>sin B cos A(3)S△ABC= r(a+b+c)(R为外接圆半径,r为内切圆半径).
高考小题突破1
考点一
三角函数的定义、诱导公式及同角三角函数的关系
(2)(2022·江苏南京、盐城二模)利用诱导公式可以将任意角的三角函数值转化为0°~90°之间角的三角函数值,而这个范围内的三角函数值又可以通过查三角函数表得到.下表为部分锐角的正弦值,则tan 1 600°的值为(小数点后保留2位有效数字)( )
α 10° 20° 30° 40°
sin α 0.173 6 0.342 0 0.500 0 0.642 7
α 50° 60° 70° 80°
sin α 0.766 0 0.866 0 0.939 7 0.984 8
A.-0.42 B.-0.36 C.0.36 D.0.42
答案 (1)D (2)B
规律方法
1.象限角的三角函数值的符号的判断:一全正,二正弦,三正切,四余弦.
2.利用诱导公式化任意角的三角函数为锐角三角函数值,其步骤:去负—脱周—化锐.
3.同角三角函数的求值:只要已知其一种三角函数值就能通过平方关系及商数关系求另外两种三角函数值.
考点二
三角函数的图象
考向1三角函数的图象变换
(2)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)是偶函数,将y=f(x)的图象沿x轴向左平移 个单位长度,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为y=g(x).已知y=g(x)的图象的相邻对称中心之间的距离为2π.若y=g(x)的图象在其某条对称轴处对应的函数值为-2,则g(x)在[0,π]上的最大值为 .
∵y=g(x)的图象的相邻对称中心之间的距离为2π.
规律方法
1.平移变换
沿x轴平移:由y=f(x)的图象变为y=f(x+φ)的图象时,“左加右减”,即φ>0,左移;φ<0,右移.沿y轴平移:由y=f(x)的图象变为y=f(x)+k的图象时,“上加下减”,即k>0,上移;k<0,下移.
2.伸缩变换
沿x轴伸缩:若ω>0,A>0,由y=f(x)变为y=f(ωx)时,点的纵坐标不变,横坐标变为原来的 倍;沿y轴伸缩:由y=f(x)变为y=Af(x)时,点的横坐标不变,纵坐标变为原来的A倍.
答案 (1)D (2)C
考向2三角函数的图象与其解析式
典例突破3(1)(2022·安徽蚌埠质检三)函数f(x)=2sin(ωx+φ)(ω>0,|φ|< )的图象如图所示,则ω的值为( )
答案 (1)C (2)A
规律方法
求函数y=Asin(ωx+φ)+B(A>0,ω>0)解析式的方法
字母 确定途径 说明
A,B 由最值确定
ω 由函数的周期确定 利用图象中最高点、最低点与x轴交点的横坐标确定周期
φ 由图象上的特殊点确定 代入图象上某一个已知点的坐标,表示出φ后,利用已知范围求φ
答案 A
x1,x2,x3(x1规律方法
函数f(x)=Asin(ωx+φ)(x∈R)的周期、最值、对称轴、对称中心之间的联系
函数的图象与x轴的任意一个交点都是对称中心,且函数的对称轴必过两相邻对称中心的中点;f(x)的最大值或者最小值必在对称轴处;对称轴之间的距离是半个周期的整数倍;对称中心之间的距离也是半个周期的整数倍;对称轴与对称中心的距离是四分之一周期的整数倍.这里所说的周期都是最小正周期.
答案 (1)D (2)D
解析 (1)由题意,因为f(x)=sin 2x,
所以g(x)=sin 2(x-φ),
考点三
三角函数的性质
典例突破5(1)(2022·陕西金台一模)已知函数f(x)=sin x-cos x,则下列结论中正确的是( )
A.f(x)的最小正周期为π
B.f(x)的最大值为2
规律方法
求三角函数性质的一般方法
通过化简、利用辅助角公式将三角函数化为f(x)=Asin(ωx+φ)后,无论是求函数的单调区间,还是求对称中心以及对称轴都将ωx+φ看作一个整体,利用y=sin x的性质来构造不等式或等式来求.
答案 (1)A (2)A
高考小题突破2
考点一
和、差、倍、半公式的应用
A.tan(α+β)=-1 B.tan(α+β)=1
C.tan(α-β)=-1 D.tan(α-β)=1
规律方法
1.三角函数公式的三种用法
运用两角和与差的三角函数公式时,不但要熟练公式的直接应用,即正用,而且要熟悉公式的逆用及变形,如tan α+tan β=tan(α+β)(1-tan αtan β)和二倍角的余弦公式的多种变形等.公式的逆用和变形应用更能开拓思路,培养从正向思维向逆向思维转化的能力.
2.应用三角函数公式的注意点
在应用三角函数和、差、倍、半角公式时,要注意观察角之间的和、差、倍、半、互补、互余等关系.
答案 (1)A (2)B (3)D
考点二
三角函数与三角变换的综合
典例突破2(1) (2022·广西柳州三模)已知函数f(x)=sin(πx+φ)在某个周期的图象如图所示,A,B分别是f(x)图象的最高点与最低点,C是f(x)图象与x轴的交点,则tan∠ACB=( )
(2)已知函数f(x)=2sin 2x(sin 2x+cos 2x)-1,则下列说法正确的是( )
A.f(x)的最小正周期为π
B.f(x)的最大值为2
答案 (1)A (2)C
规律方法
求三角变换与三角函数综合问题的思路
通过变换把函数化为y=Asin(ωx+φ)的形式再研究其性质,解题时注意观察角、名、结构等特征,注意利用整体思想解决相关问题.
答案 B
考点三
应用正、余弦定理解三角形
(3)某市为表彰先进单位,制作了一批奖杯,奖杯的剖面如图所示,其中扇形OAB的半径为10,∠PBA=∠QAB=60°,AQ=QP=PB,若按此方案设计,工艺制造厂发现,当OP最长时,该奖杯比较美观,此时∠AOB= .
(3)设∠ABO=θ,则AB=20cos θ,
又AB=QP+2PBcos 60°=2PB,所以PB=10cos θ,
规律方法
正、余弦定理的应用范围
对点练3(1)在△ABC中,角A,B,C的对边分别为a,b,c,如果a,b,c成等差数
(2) 如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从点A测得点M的仰角∠MAN=60°,点C的仰角∠BAC=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100 m,则山高MN= m.
答案 (1)A (2)150 (3)C
考点四
正、余弦定理与三角变换的综合
典例突破4(1)(2022·河南洛阳一模)已知△ABC中,AB=5,AC=4,则当函数
规律方法
解三角形的基本策略
(1)对题目中的已知条件要灵活运用正弦定理、余弦定理以实现边角互化.
(2)在三角形中进行三角变换要注意隐含条件:A+B+C=π,这样可以减少未知数的个数.
(2)(2022·四川成都二模)已知△ABC中,角A,B,C的对边分别为a,b,c.若c=1,4a2cos2B+4b2sin2A=3b2-3,则cos A的最小值为( )
答案 (1)C (2)C
(2)由题意,得4a2-4a2sin2B+4b2sin2A=3b2-3,
设△ABC外接圆的直径为2R,
则4a2-16R2sin2Asin2B+16R2sin2Bsin2A=3b2-3,
培优拓展
应用三角公式解决问题的三个变换角度
(1)变角:目的是沟通题设条件与结论中所涉及的角,其手法通常是“配凑”或“换元”.
(2)变名:通过变换函数名称达到减少函数种类的目的,其手法通常有“切化弦”“升幂与降幂”等.
(3)变式:根据式子的结构特征进行变形,使其更贴近某个公式或某个期待的目标,其手法通常有:“常值代换”“逆用变用公式”“通分约分”“分解与组合”“配方与平方”等.
问题提出
结论应用
类型1三角变换中的变角
类型2三角变换中的变名
类型3三角变换中的变式
答案 (1)D (2)C
类型4解三角形中的变角、变式
例4(12分)△ABC的内角A,B,C的对边分别为a,b,c.设
(sin B-sin C)2=sin2A-sin Bsin C.
(1)求A;
(2)若 a+b=2c,求sin C.
【评分标准—找回丢分】
【教师讲评—触类旁通】
分析1:常用的变角技巧
(1)已知角与特殊角的变换,如75°=30°+45°;
分析2:常用的变式技巧
(1)解决与三角函数性质有关的问题,常先将它的表达式统一化为y=Asin(ωx+φ)+B的形式;
(2)涉及sin x±cos x,sin x·cos x的问题,常做换元处理,如令t=sin x±cos x∈
(3)在解决三角形的问题时,常利用正、余弦定理化边为角或化角为边等.
【举一反三】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b+c=2a,3csin B=4asin C.
(1)求cos B的值;
高考满分大题一
考点一
三角函数与三角变换的综合
规律方法
1.通过变换把函数化为y=Asin(ωx+φ)的形式再研究其性质,解题时注意观察角、名、结构等特征,注意利用整体思想解决相关问题.
2.三角变换的总体思路是化异为同,目的是通过消元减少未知量的个数.如:把三角函数式中的异名、异角、异次化为同名、同角、同次,或把未知角用已知角表示,或把未知角通过三角变换化为已知角.
考点二
利用正弦定理、余弦定理解三角形
典例突破2(一题多解)(2022·山东济南一模)已知△ABC的内角A,B,C的对边分别为a,b,c,满足bsin A= acos B.
(1)求B;
(2)若D为边AC的中点,且BD= ,c=4,求a.
规律方法
解三角形的基本策略
对点练2(2022·河南濮阳一模)在△ABC中,内角A,B,C的对边分别是a,b,c,且3b2+3c2-4 bc=3a2.
(1)求sin A;
(2)若3csin A= asin B,△ABC的面积为 ,求c.
对点练3(一题多解)在四边形ABCD中,AC与BD交于点E,AB=2BC=2CD=4.
考点三
三角函数与解三角形的综合
(1)求角B的大小;
(2)若b=3,a=2c,求△ABC的面积.
规律方法
对于在三角形中求解有关三角函数的图象和性质的题目,时刻不要忘记对角的范围的限制,特别是求三角函数值的范围或最值时,先要把自变量的取值范围求出来,再利用三角函数的图象或性质确定函数值的范围.
解 (1)分析条件知①②矛盾,②③矛盾,故满足的条件为①③,由③知T=2π,
a2=4=b2+c2-bc≥bc,
当且仅当b=c=2时等号成立,
考点四
三角变换与解三角形的综合
典例突破4(2022·河南平顶山二模)在△ABC中,内角A,B,C的对边分别是a,b,c,其中c=4,且满足acos C=csin A.
(1)求角C的大小;
解 (1)∵acos C=csin A,
∴由正弦定理得sin Acos C=sin Csin A,
∵sin A>0,∴cos C=sin C,∵cos C≠0,∴tan C=1,
∵C∈(0,π),∴C= .
解题技巧
在三角形中进行三角变换的技巧
在三角形中进行三角变换,它是在新的载体上进行的三角变换,一是它必然要用到三角形的内角和定理,正、余弦定理及有关三角形的性质,及时进行边角转化,有利于发现解决问题的思路;二是它毕竟是三角变换,只是角的范围受到限制,因此常见的三角变换方法和原则都是适用的,注意“三统一”,即“统一角、统一函数、统一结构”是使问题获得解决的突破口.
对点练5(2022·云南昆明一中一模)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知ac=2(a2-b2-c2),且sin A=2sin B.
(1)求A的大小;
(2)求cos(A-2B)的值.
解 (1)∵sin A=2sin B,∴由正弦定理得a=2b,
又∵ac=2(a2-b2-c2),
对点练6(2020·浙江·18)在锐角三角形ABC中,角A,B,C所对的边分别为a,b,c,已知2bsin A- a=0.
(1)求角B的大小;
(2)求cos A+cos B+cos C的取值范围.
考点五
三角函数、三角变换与解三角形的综合
典例突破5(2022·河南顶级名校4月联考)已知函数y=Asin(ωx+φ)
再把所得曲线上的点的横坐标变为原来的2倍(纵坐标不变),得到函数f(x)的图象.设g(x)=f(x)·sin x.
(1)求函数g(x)的最小正周期T;
在△ABC中,
由余弦定理得(2m)2=36+x2-12xcos∠BAC=36+x2+6x.
∴2x2-4=36+x2+6x,
∴x=-4(舍去),或x=10,即AC=10.
规律方法
解三角函数、三角变换与三角形综合题的思路:
一般是由正弦定理、余弦定理求出某个量作为下面问题的已知量,然后利用三角变换,将所求的量化为f(x)=Asin(ωx+φ)或f(x)=Acos(ωx+φ)的形式,最终求出结果.
对点练7(2022·河南郑州二模)在△ABC中,内角A,B,C所对的边分别为a,b,c,△ABC的面积为S,若 =(2b-a)(a2+b2-c2).
(1)求角C;
(2)求sin A+sin B的取值范围.
典例突破6(12分)在△ABC中,a,b,c分别为内角A,B,C的对边,sin2A+sin2C=sin2B+sin Asin C.
(1)求角B的大小;
(2)若△ABC为锐角三角形,b= ,求2a-c的取值范围.
【评分标准—找回丢分】
【教师讲评—触类旁通】
分析1:在(1)中,求角B的大小,因为等式sin2A+sin2C=sin2B+sin Asin C含有三个未知数,显然求不出,应用正弦定理将三个角的关系转化为三边关系,再应用余弦定理求出;
分析2:在(2)中,2a-c也含有两个未知数,需化为一个未知数角C的式子,由
【举一反三】(2022·河南洛阳一模)在△ABC中,内角A,B,C的对边分别为a,b,c,且bcos Asin C+asin Bcos C= b.
(1)求角B的大小;
(2)若△ABC为锐角三角形,b=3,求a+c的取值范围.
专题一 三角函数与解三角形
上篇
内容索引
01
02
03
高考小题突破1 三角函数的图象与性质
高考小题突破2 三角变换与解三角形
培优拓展 三角变换与解三角形中的变“角、名、式”
04
◎高考满分大题一 三角函数与解三角形
考情分析 三角函数与解三角形是高考的考点题型,从近五年的高考试题来看,呈现较强的规律性,每年的题量和分值一般是三个小题共15分或一个小题加一个大题共17分,两种情况间隔出现.该部分常考查的内容有三角函数的图象与性质,三角恒等变换与诱导公式,利用正弦定理和余弦定理解三角形.在解题过程中,要注意三角恒等变换公式的多样性和灵活性,注意题目中隐含的各种限制条件,选择合理的方法解题.
备考策略 1.让学生牢记公式概念,夯实基础.三角题几乎都要用到各类公式,牢记公式是进行运算的基础.看似简单,但是总有学生因公式应用错误而丢分,所以教学中要勤督促、多提问、常反复、多检查.
2.对于各类问题多整理,特点要记清,方法要用对.例如f(x)=Asin(ωx+φ)从整体考虑易于求单调区间、值域等,但有些函数化不成这种形式,如求f(x)=2sin x+sin 2x的值域,要用研究其他函数的方法去研究,必要时要用导数解决.还有在解三角形中,边化角、角化边都存在选择恰当的解题方向问题.
备考策略 3.注意细节,杜绝失误.三角问题虽然整体难度不大,但是细小问题较多,容易失误.例如:图象变换中的平移变换,先看函数名称是否相同,再看自变量系数,再确定平移方向及单位;再如三角求值问题中角的范围的考查等.
4.重视数学思想方法的应用.三角中常用的数学思想一是转化与化归思想:在三角恒等变换,利用正、余弦定理进行边角转化中应用广泛;二是数形结合思想:在求三角函数的最值(值域)及三角函数零点问题,方程或不等式问题时,要强化数形结合思想的应用.
真题感悟
答案 D
2.(2020·全国Ⅰ·文7)设函数f(x)=cos(ωx+ )在[-π,π]的图象大致如图,则f(x)的最小正周期为( )
答案 C
答案 D
解析 设BC=x,由余弦定理得19=4+x2-2×2x·cos 120°,解得x=3或x=-5(舍).故选D.
答案 A
5.(2021·全国乙·文15)记△ABC的内角A,B,C的对边分别为a,b,c,面积为 ,B=60°,a2+c2=3ac,则b= .
6.(2021·全国甲·文15)已知函数f(x)=2cos(ωx+φ)的部分图象如图所示,则
f( )= .
7.(2022·全国乙·文17)记△ABC的内角A,B,C的对边分别为a,b,c,已知
sin Csin(A-B)=sin Bsin(C-A).
(1)若A=2B,求C;
(2)证明:2a2=b2+c2.
(1)解 ∵sin Csin(A-B)=sin Bsin(C-A),A=2B,
∴sin Csin B=sin Bsin(C-A).
又sin B>0,∴sin C=sin(C-A).
(2)证明 (方法一)∵sin Csin(A-B)=sin Bsin(C-A),
∴sin C(sin A·cos B-cos Asin B)=sin B(sin Ccos A-cos Csin A),
即sin C·sin Acos B-sin Ccos Asin B=sin Bsin Ccos A-sin Bcos Csin A,
即sin A(sin Ccos B+cos Csin B)=2sin Bsin Ccos A,
即sin Asin(B+C)=2sin Bsin Ccos A,
即sin2A=2sin Bsin Ccos A.
即a2=b2+c2-a2,故2a2=b2+c2.
(方法二)∵sin Csin(A-B)=sin Bsin(C-A),∴sin Csin A·cos B-sin Csin Bcos A
=sin Bsin Ccos A-sin Bsin Acos C,
知识精要
1.三角函数的定义
名师点析
若|OP|=1,则sin α=y,cos α=x.若α∈(0, ),则sin α<α
名师点析
(1)平方关系经常被逆用,即“1”的代换;
(2)商数关系也经常被逆用,即“切化弦”.
3.三角函数的图象与性质
知识点 内容
三角函数的图象与性质 (1)y=sin x图象的对称轴方程为x= +kπ,k∈Z,对称中心为(kπ,0),k∈Z;
图象与x轴的交点
y=cos x图象的对称轴方程为x=kπ,k∈Z,对称中心为
( +kπ,0),k∈Z
对称轴过图象的最高点或最低点
名师点析
正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个最小正周期.
4.两角和与差的正弦、余弦、正切公式
知识点 内容
两角和与差的正弦、余弦、正切公式 sin(α±β)=sin αcos β±cos αsin β;
cos(α±β)=cos αcos β sin αsin β;
tan(α±β)=
名师点析
两角和与差的正切公式的常用变式:tan α±tan β=(1 tan αtan β)tan(α±β).
5.二倍角公式及降幂公式
名师点析
由降幂公式开方并作角的代换得半角公式:
6.正弦、余弦定理
名师点析
三角形的三个常用结论
(1)tan A+tan B+tan C=tan A·tan B·tan C.
(2)A>B a>b sin A>sin B cos A
高考小题突破1
考点一
三角函数的定义、诱导公式及同角三角函数的关系
(2)(2022·江苏南京、盐城二模)利用诱导公式可以将任意角的三角函数值转化为0°~90°之间角的三角函数值,而这个范围内的三角函数值又可以通过查三角函数表得到.下表为部分锐角的正弦值,则tan 1 600°的值为(小数点后保留2位有效数字)( )
α 10° 20° 30° 40°
sin α 0.173 6 0.342 0 0.500 0 0.642 7
α 50° 60° 70° 80°
sin α 0.766 0 0.866 0 0.939 7 0.984 8
A.-0.42 B.-0.36 C.0.36 D.0.42
答案 (1)D (2)B
规律方法
1.象限角的三角函数值的符号的判断:一全正,二正弦,三正切,四余弦.
2.利用诱导公式化任意角的三角函数为锐角三角函数值,其步骤:去负—脱周—化锐.
3.同角三角函数的求值:只要已知其一种三角函数值就能通过平方关系及商数关系求另外两种三角函数值.
考点二
三角函数的图象
考向1三角函数的图象变换
(2)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)是偶函数,将y=f(x)的图象沿x轴向左平移 个单位长度,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为y=g(x).已知y=g(x)的图象的相邻对称中心之间的距离为2π.若y=g(x)的图象在其某条对称轴处对应的函数值为-2,则g(x)在[0,π]上的最大值为 .
∵y=g(x)的图象的相邻对称中心之间的距离为2π.
规律方法
1.平移变换
沿x轴平移:由y=f(x)的图象变为y=f(x+φ)的图象时,“左加右减”,即φ>0,左移;φ<0,右移.沿y轴平移:由y=f(x)的图象变为y=f(x)+k的图象时,“上加下减”,即k>0,上移;k<0,下移.
2.伸缩变换
沿x轴伸缩:若ω>0,A>0,由y=f(x)变为y=f(ωx)时,点的纵坐标不变,横坐标变为原来的 倍;沿y轴伸缩:由y=f(x)变为y=Af(x)时,点的横坐标不变,纵坐标变为原来的A倍.
答案 (1)D (2)C
考向2三角函数的图象与其解析式
典例突破3(1)(2022·安徽蚌埠质检三)函数f(x)=2sin(ωx+φ)(ω>0,|φ|< )的图象如图所示,则ω的值为( )
答案 (1)C (2)A
规律方法
求函数y=Asin(ωx+φ)+B(A>0,ω>0)解析式的方法
字母 确定途径 说明
A,B 由最值确定
ω 由函数的周期确定 利用图象中最高点、最低点与x轴交点的横坐标确定周期
φ 由图象上的特殊点确定 代入图象上某一个已知点的坐标,表示出φ后,利用已知范围求φ
答案 A
x1,x2,x3(x1
函数f(x)=Asin(ωx+φ)(x∈R)的周期、最值、对称轴、对称中心之间的联系
函数的图象与x轴的任意一个交点都是对称中心,且函数的对称轴必过两相邻对称中心的中点;f(x)的最大值或者最小值必在对称轴处;对称轴之间的距离是半个周期的整数倍;对称中心之间的距离也是半个周期的整数倍;对称轴与对称中心的距离是四分之一周期的整数倍.这里所说的周期都是最小正周期.
答案 (1)D (2)D
解析 (1)由题意,因为f(x)=sin 2x,
所以g(x)=sin 2(x-φ),
考点三
三角函数的性质
典例突破5(1)(2022·陕西金台一模)已知函数f(x)=sin x-cos x,则下列结论中正确的是( )
A.f(x)的最小正周期为π
B.f(x)的最大值为2
规律方法
求三角函数性质的一般方法
通过化简、利用辅助角公式将三角函数化为f(x)=Asin(ωx+φ)后,无论是求函数的单调区间,还是求对称中心以及对称轴都将ωx+φ看作一个整体,利用y=sin x的性质来构造不等式或等式来求.
答案 (1)A (2)A
高考小题突破2
考点一
和、差、倍、半公式的应用
A.tan(α+β)=-1 B.tan(α+β)=1
C.tan(α-β)=-1 D.tan(α-β)=1
规律方法
1.三角函数公式的三种用法
运用两角和与差的三角函数公式时,不但要熟练公式的直接应用,即正用,而且要熟悉公式的逆用及变形,如tan α+tan β=tan(α+β)(1-tan αtan β)和二倍角的余弦公式的多种变形等.公式的逆用和变形应用更能开拓思路,培养从正向思维向逆向思维转化的能力.
2.应用三角函数公式的注意点
在应用三角函数和、差、倍、半角公式时,要注意观察角之间的和、差、倍、半、互补、互余等关系.
答案 (1)A (2)B (3)D
考点二
三角函数与三角变换的综合
典例突破2(1) (2022·广西柳州三模)已知函数f(x)=sin(πx+φ)在某个周期的图象如图所示,A,B分别是f(x)图象的最高点与最低点,C是f(x)图象与x轴的交点,则tan∠ACB=( )
(2)已知函数f(x)=2sin 2x(sin 2x+cos 2x)-1,则下列说法正确的是( )
A.f(x)的最小正周期为π
B.f(x)的最大值为2
答案 (1)A (2)C
规律方法
求三角变换与三角函数综合问题的思路
通过变换把函数化为y=Asin(ωx+φ)的形式再研究其性质,解题时注意观察角、名、结构等特征,注意利用整体思想解决相关问题.
答案 B
考点三
应用正、余弦定理解三角形
(3)某市为表彰先进单位,制作了一批奖杯,奖杯的剖面如图所示,其中扇形OAB的半径为10,∠PBA=∠QAB=60°,AQ=QP=PB,若按此方案设计,工艺制造厂发现,当OP最长时,该奖杯比较美观,此时∠AOB= .
(3)设∠ABO=θ,则AB=20cos θ,
又AB=QP+2PBcos 60°=2PB,所以PB=10cos θ,
规律方法
正、余弦定理的应用范围
对点练3(1)在△ABC中,角A,B,C的对边分别为a,b,c,如果a,b,c成等差数
(2) 如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从点A测得点M的仰角∠MAN=60°,点C的仰角∠BAC=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100 m,则山高MN= m.
答案 (1)A (2)150 (3)C
考点四
正、余弦定理与三角变换的综合
典例突破4(1)(2022·河南洛阳一模)已知△ABC中,AB=5,AC=4,则当函数
规律方法
解三角形的基本策略
(1)对题目中的已知条件要灵活运用正弦定理、余弦定理以实现边角互化.
(2)在三角形中进行三角变换要注意隐含条件:A+B+C=π,这样可以减少未知数的个数.
(2)(2022·四川成都二模)已知△ABC中,角A,B,C的对边分别为a,b,c.若c=1,4a2cos2B+4b2sin2A=3b2-3,则cos A的最小值为( )
答案 (1)C (2)C
(2)由题意,得4a2-4a2sin2B+4b2sin2A=3b2-3,
设△ABC外接圆的直径为2R,
则4a2-16R2sin2Asin2B+16R2sin2Bsin2A=3b2-3,
培优拓展
应用三角公式解决问题的三个变换角度
(1)变角:目的是沟通题设条件与结论中所涉及的角,其手法通常是“配凑”或“换元”.
(2)变名:通过变换函数名称达到减少函数种类的目的,其手法通常有“切化弦”“升幂与降幂”等.
(3)变式:根据式子的结构特征进行变形,使其更贴近某个公式或某个期待的目标,其手法通常有:“常值代换”“逆用变用公式”“通分约分”“分解与组合”“配方与平方”等.
问题提出
结论应用
类型1三角变换中的变角
类型2三角变换中的变名
类型3三角变换中的变式
答案 (1)D (2)C
类型4解三角形中的变角、变式
例4(12分)△ABC的内角A,B,C的对边分别为a,b,c.设
(sin B-sin C)2=sin2A-sin Bsin C.
(1)求A;
(2)若 a+b=2c,求sin C.
【评分标准—找回丢分】
【教师讲评—触类旁通】
分析1:常用的变角技巧
(1)已知角与特殊角的变换,如75°=30°+45°;
分析2:常用的变式技巧
(1)解决与三角函数性质有关的问题,常先将它的表达式统一化为y=Asin(ωx+φ)+B的形式;
(2)涉及sin x±cos x,sin x·cos x的问题,常做换元处理,如令t=sin x±cos x∈
(3)在解决三角形的问题时,常利用正、余弦定理化边为角或化角为边等.
【举一反三】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b+c=2a,3csin B=4asin C.
(1)求cos B的值;
高考满分大题一
考点一
三角函数与三角变换的综合
规律方法
1.通过变换把函数化为y=Asin(ωx+φ)的形式再研究其性质,解题时注意观察角、名、结构等特征,注意利用整体思想解决相关问题.
2.三角变换的总体思路是化异为同,目的是通过消元减少未知量的个数.如:把三角函数式中的异名、异角、异次化为同名、同角、同次,或把未知角用已知角表示,或把未知角通过三角变换化为已知角.
考点二
利用正弦定理、余弦定理解三角形
典例突破2(一题多解)(2022·山东济南一模)已知△ABC的内角A,B,C的对边分别为a,b,c,满足bsin A= acos B.
(1)求B;
(2)若D为边AC的中点,且BD= ,c=4,求a.
规律方法
解三角形的基本策略
对点练2(2022·河南濮阳一模)在△ABC中,内角A,B,C的对边分别是a,b,c,且3b2+3c2-4 bc=3a2.
(1)求sin A;
(2)若3csin A= asin B,△ABC的面积为 ,求c.
对点练3(一题多解)在四边形ABCD中,AC与BD交于点E,AB=2BC=2CD=4.
考点三
三角函数与解三角形的综合
(1)求角B的大小;
(2)若b=3,a=2c,求△ABC的面积.
规律方法
对于在三角形中求解有关三角函数的图象和性质的题目,时刻不要忘记对角的范围的限制,特别是求三角函数值的范围或最值时,先要把自变量的取值范围求出来,再利用三角函数的图象或性质确定函数值的范围.
解 (1)分析条件知①②矛盾,②③矛盾,故满足的条件为①③,由③知T=2π,
a2=4=b2+c2-bc≥bc,
当且仅当b=c=2时等号成立,
考点四
三角变换与解三角形的综合
典例突破4(2022·河南平顶山二模)在△ABC中,内角A,B,C的对边分别是a,b,c,其中c=4,且满足acos C=csin A.
(1)求角C的大小;
解 (1)∵acos C=csin A,
∴由正弦定理得sin Acos C=sin Csin A,
∵sin A>0,∴cos C=sin C,∵cos C≠0,∴tan C=1,
∵C∈(0,π),∴C= .
解题技巧
在三角形中进行三角变换的技巧
在三角形中进行三角变换,它是在新的载体上进行的三角变换,一是它必然要用到三角形的内角和定理,正、余弦定理及有关三角形的性质,及时进行边角转化,有利于发现解决问题的思路;二是它毕竟是三角变换,只是角的范围受到限制,因此常见的三角变换方法和原则都是适用的,注意“三统一”,即“统一角、统一函数、统一结构”是使问题获得解决的突破口.
对点练5(2022·云南昆明一中一模)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知ac=2(a2-b2-c2),且sin A=2sin B.
(1)求A的大小;
(2)求cos(A-2B)的值.
解 (1)∵sin A=2sin B,∴由正弦定理得a=2b,
又∵ac=2(a2-b2-c2),
对点练6(2020·浙江·18)在锐角三角形ABC中,角A,B,C所对的边分别为a,b,c,已知2bsin A- a=0.
(1)求角B的大小;
(2)求cos A+cos B+cos C的取值范围.
考点五
三角函数、三角变换与解三角形的综合
典例突破5(2022·河南顶级名校4月联考)已知函数y=Asin(ωx+φ)
再把所得曲线上的点的横坐标变为原来的2倍(纵坐标不变),得到函数f(x)的图象.设g(x)=f(x)·sin x.
(1)求函数g(x)的最小正周期T;
在△ABC中,
由余弦定理得(2m)2=36+x2-12xcos∠BAC=36+x2+6x.
∴2x2-4=36+x2+6x,
∴x=-4(舍去),或x=10,即AC=10.
规律方法
解三角函数、三角变换与三角形综合题的思路:
一般是由正弦定理、余弦定理求出某个量作为下面问题的已知量,然后利用三角变换,将所求的量化为f(x)=Asin(ωx+φ)或f(x)=Acos(ωx+φ)的形式,最终求出结果.
对点练7(2022·河南郑州二模)在△ABC中,内角A,B,C所对的边分别为a,b,c,△ABC的面积为S,若 =(2b-a)(a2+b2-c2).
(1)求角C;
(2)求sin A+sin B的取值范围.
典例突破6(12分)在△ABC中,a,b,c分别为内角A,B,C的对边,sin2A+sin2C=sin2B+sin Asin C.
(1)求角B的大小;
(2)若△ABC为锐角三角形,b= ,求2a-c的取值范围.
【评分标准—找回丢分】
【教师讲评—触类旁通】
分析1:在(1)中,求角B的大小,因为等式sin2A+sin2C=sin2B+sin Asin C含有三个未知数,显然求不出,应用正弦定理将三个角的关系转化为三边关系,再应用余弦定理求出;
分析2:在(2)中,2a-c也含有两个未知数,需化为一个未知数角C的式子,由
【举一反三】(2022·河南洛阳一模)在△ABC中,内角A,B,C的对边分别为a,b,c,且bcos Asin C+asin Bcos C= b.
(1)求角B的大小;
(2)若△ABC为锐角三角形,b=3,求a+c的取值范围.
同课章节目录
