2023届高考二轮总复习课件(适用于老高考旧教材) 数学(文)第2讲 高考客观题速解技巧 课件(共50张PPT)
文档属性
| 名称 | 2023届高考二轮总复习课件(适用于老高考旧教材) 数学(文)第2讲 高考客观题速解技巧 课件(共50张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 17:32:28 | ||
图片预览


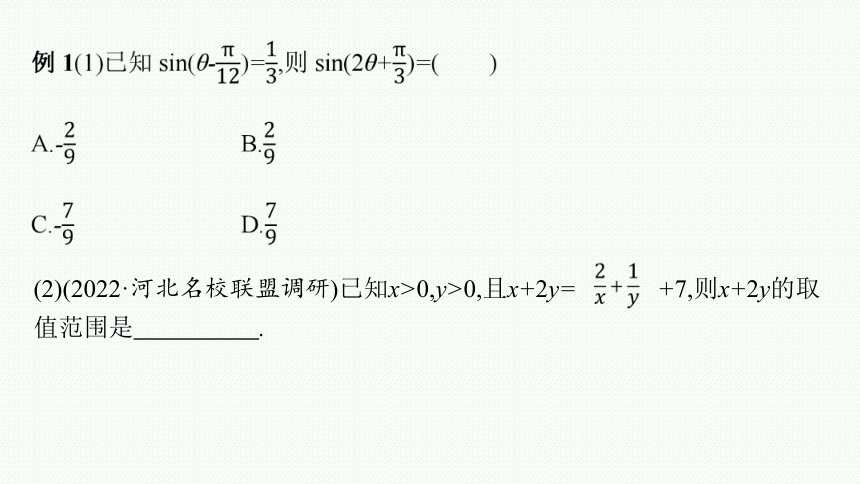









文档简介
(共50张PPT)
第2讲 高考客观题速解技巧
序篇
高考的选择题、填空题注重多个知识点的小型综合,渗透各种数学思想和方法,体现了利用基础知识深度地考基础考能力的导向;使作为中低档题的选择题、填空题成为具备较佳区分度的基本题型.因此能否在选择题、填空题上获取高分,对高考数学成绩影响重大.解答选择题的基本策略是准确、迅速.
(2)(2022·河北名校联盟调研)已知x>0,y>0,且x+2y= +7,则x+2y的取值范围是 .
答案 (1)D (2)[8,+∞)
t=x+2y,则(t-7)t≥8,即t2-7t-8≥0,即(t+1)·(t-8)≥0,解得t≥8或t≤-1(舍去).
∴x+2y的取值范围是[8,+∞).故答案为[8,+∞).
规律方法
换元的方法有:整体换元、三角换元等.整体换元又有两种类型,一是在已知或者未知中,某个代数式几次出现(有时变形才能发现),用字母来代替它从而简化问题;二是条件中的代数式与结论的代数式都含某个变量,将条件中的代数式用字母代替,从中解出变量代入结论,易发现条件与结论的关系.三角换元,应用于去根号,或者变换为三角形式易求,主要利用已知代数式与三角函数知识的某种联系进行换元.
对点练1(1)(2022·湖北荆州沙市中学期末)已知点A(3,0),B(0,2), O为坐标原点,点P为圆(x-3)2+(y-2)2=1上任意一点,设 (λ,μ∈R),则9λ+8μ的最大值为( )
A.12 B.17
C.22 D.27
解析 (1)由点P为圆(x-3)2+(y-2)2=1上任意一点,可设P(3+cos θ,2+sin θ),其中0≤θ≤2π.
则9λ+8μ=9+3cos θ+8+4sin θ=5sin(θ+φ)+17,
其中tan φ= ,因为0≤θ≤2π,
所以当sin(θ+φ)=1时,9λ+8μ取得最大值,为22.故选C.
考向2特值、特例法
例2(1)(2020·山东模考卷)若a>b>c>1且acA.logab>logbc>logca B.logcb>logba>logac
C.logcb>logab>logca D.logba>logcb>logac
(2)(2022·安徽蚌埠质检三)如图所示,在梯形ABCD中,AB∥DC且AB=2DC,点E为线段BC的靠近点C的一个四等分点,点F为线段AD的中点,AE与BF交
答案 (1)B (2)C
解析 (1)因为a>b>c>1且ac1>logab,故A,C
(2)(方法一)将条件中梯形特殊化为直角梯形,且AD=DC,
设DC=2,建立如图所示的平面直角坐标系,则有
A(0,0),D(0,2),C(2,2),B(4,0),F(0,1),所以BC的中点坐标为G(3,1),
规律方法
1.特值、特例法是在题设普遍条件都成立的情况下,用特殊值(取的越简单越好)进行探求,从而清晰、快捷地得到正确的答案,即通过对特殊情况的研究来判断一般规律,从而“小题小做”或“小题巧做”.
2.当题目的已知条件中含有某些不确定的量时,可针对题目中变化的不定量选取一些符合条件的特殊值(或特殊函数、特殊角、特殊数列、特殊图形、图形特殊位置、特殊点、特殊方程、特殊模型等)进行处理,从而得出探求的结论.这样可大大地简化推理、论证的过程.
A.a>b>c B.b>c>a
C.b>a>c D.c>a>b
(2) 如图所示,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,
(2)所求的问题是个定值问题,“在△ABC中”和在特殊△ABC中所求的值相等,所以将所给条件“在△ABC中”特殊化为“在等边三角形ABC中”.如图所示.
考向3排除法(针对选择题)
例3(1)(2022·河南名校联盟一模)已知α是第二象限角,则( )
A.cos α>0 B.sin α<0
C.sin 2α<0 D.tan α>0
(2)(2020·全国Ⅱ·文5)已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是( )
A.a+2b B.2a+b
C.a-2b D.2a-b
(3)函数f(x)= (其中e为自然对数的底数)的图象大致为( )
答案 (1)C (2)D (3)A
解析 (1)因为α是第二象限角,所以cos α<0,sin α>0,tan α<0,故选项ABC都错,故选C.
对于D,(2a-b)·b=2a·b-b2=0,故2a-b与b垂直.故选D.
规律方法
数学选择题的解题本质就是去伪存真,舍弃不符合题目要求的选项,找到符合题意的正确结论.排除法(又叫筛选法)就是通过观察分析或推理运算各项提供的信息或通过特例,对于不符合题意的选项逐一剔除,从而获得正确的结论.
对点练3(1)(2020·浙江·4)函数y=xcos x+sin x在区间[-π,π]上的图象可能是( )
(2)(2022·山西长治模拟预测)若函数f(x)对定义域中的任意取值x都满足f(x+2)=f(x),则f(x)可以是( )
A.f(x)=(x-1)2 B.f(x)=|x-2|
答案 (1)A (2)D
考向4解析法
(2)(2022·山东济宁一模)在边长为6的菱形ABCD中,A= ,现将△ABD沿BD折起,当三棱锥A-BCD的体积最大时,三棱锥A-BCD的外接球的表面积为 .
答案 (1)B (2)60π
解析 (1)以O为坐标原点,建立平面直角坐标系如图所示,过点A作x轴的垂
(2)如图所示,取BD的中点O为坐标原点,直线OC为x轴,直线BD为y轴,过点O垂直于平面BCD的直线为z轴,建立空间直角坐标系,当点A在z轴上时,
是OA上靠近点O的三等分点,取点F是OC上靠近点O的三等分点,则点E,F分别是等边三角形ABD与等边三角形CBD的中心.分别过点E,F作直线垂直于平面ABD与平面CBD,设这两条直线交于点G,则点G就是三棱锥A-BCD
所以三棱锥A-BCD的外接球的表面积为4π×15=60π.
规律方法
解析法又称坐标法,是解析几何中最基本的研究方法,它是在平面直角坐标系的基础上,把几何问题转化为代数问题,通过代数运算研究几何图形性质的方法.
答案 (1)A (2)B
考向5等价转化法
例5(1)已知直线x+y+m=0与圆x2+y2=2交于不同的两点A,B,O是坐标原点,
答案 (1)D (2)A
(2)函数f(x)过点(1,0),所以函数f(x)有且只有一个零点 函数y=-2x+a(x≤0)没有零点 函数y=2x(x≤0)与直线y=a无公共点,可得a≤0或a>1.又{a|a<0} {a|a≤0或a>1},故选A.
规律方法
等价转化法就是把未知的问题转化到在已有知识范围内可解的问题的一种重要的思想方法.通过不断地转化,可把不熟悉、不规范、复杂的问题转化为熟悉、规范、简单的问题.
对点练5(1)一给定函数y=f(x)的图象在下列图中,并且对任意a1∈(0,1),由关系式an+1=f(an)得到的数列{an},满足an+1(2)在四面体P-ABC中,△ABC为等边三角形,边长为3,PA=3,PB=4,PC=5,则四面体P-ABC的体积为( )
答案 (1)B (2)C
解析 (1)对任意a1∈(0,1),∵an+1=f(an),又an+1(2) 如图,延长CA至点D,使得AD=3,连接DB,PD,∵AD=AB=3,故△ADB为等腰三角形.
又∠DAB=180°-∠CAB=120°,
故∠ADB= (180°-120°)=30°,
∴∠ADB+∠DCB=90°,即∠DBC=90°,故CB⊥DB.∵PB=4,PC=5,BC=3,
∴PC2=PB2+BC2,∴CB⊥PB.
∵DB∩PB=B,DB 平面PBD,PB 平面PBD,∴CB⊥平面PBD.
考向6构造法
例6(1)(2022·江苏南通第一次调研)已知α,β均为锐角,且α+β- >sin β-cos α,则( )
A.sin α>sin β
B.cos α>cos β
C.cos α>sin β
D.sin α>cos β
(2)已知a>b>e,其中e是自然对数的底数,则ab与ba的大小关系为
ab ba(从“>”“=”“<”中选择一个).
答案 (1)D (2)<
规律方法
利用已知条件和结论的特殊性构造出新的数学模型,从而简化推理与计算过程,使较复杂的数学问题得到简捷的解决.构造法是建立在观察联想、分析综合的基础之上的,从曾经遇到过的类似问题中寻找灵感,构造出相应的函数、概率、几何等具体的数学模型,使问题得到快速解决.
A.cB.aC.aD.c答案 (1)B (2)D
第2讲 高考客观题速解技巧
序篇
高考的选择题、填空题注重多个知识点的小型综合,渗透各种数学思想和方法,体现了利用基础知识深度地考基础考能力的导向;使作为中低档题的选择题、填空题成为具备较佳区分度的基本题型.因此能否在选择题、填空题上获取高分,对高考数学成绩影响重大.解答选择题的基本策略是准确、迅速.
(2)(2022·河北名校联盟调研)已知x>0,y>0,且x+2y= +7,则x+2y的取值范围是 .
答案 (1)D (2)[8,+∞)
t=x+2y,则(t-7)t≥8,即t2-7t-8≥0,即(t+1)·(t-8)≥0,解得t≥8或t≤-1(舍去).
∴x+2y的取值范围是[8,+∞).故答案为[8,+∞).
规律方法
换元的方法有:整体换元、三角换元等.整体换元又有两种类型,一是在已知或者未知中,某个代数式几次出现(有时变形才能发现),用字母来代替它从而简化问题;二是条件中的代数式与结论的代数式都含某个变量,将条件中的代数式用字母代替,从中解出变量代入结论,易发现条件与结论的关系.三角换元,应用于去根号,或者变换为三角形式易求,主要利用已知代数式与三角函数知识的某种联系进行换元.
对点练1(1)(2022·湖北荆州沙市中学期末)已知点A(3,0),B(0,2), O为坐标原点,点P为圆(x-3)2+(y-2)2=1上任意一点,设 (λ,μ∈R),则9λ+8μ的最大值为( )
A.12 B.17
C.22 D.27
解析 (1)由点P为圆(x-3)2+(y-2)2=1上任意一点,可设P(3+cos θ,2+sin θ),其中0≤θ≤2π.
则9λ+8μ=9+3cos θ+8+4sin θ=5sin(θ+φ)+17,
其中tan φ= ,因为0≤θ≤2π,
所以当sin(θ+φ)=1时,9λ+8μ取得最大值,为22.故选C.
考向2特值、特例法
例2(1)(2020·山东模考卷)若a>b>c>1且ac
C.logcb>logab>logca D.logba>logcb>logac
(2)(2022·安徽蚌埠质检三)如图所示,在梯形ABCD中,AB∥DC且AB=2DC,点E为线段BC的靠近点C的一个四等分点,点F为线段AD的中点,AE与BF交
答案 (1)B (2)C
解析 (1)因为a>b>c>1且ac
(2)(方法一)将条件中梯形特殊化为直角梯形,且AD=DC,
设DC=2,建立如图所示的平面直角坐标系,则有
A(0,0),D(0,2),C(2,2),B(4,0),F(0,1),所以BC的中点坐标为G(3,1),
规律方法
1.特值、特例法是在题设普遍条件都成立的情况下,用特殊值(取的越简单越好)进行探求,从而清晰、快捷地得到正确的答案,即通过对特殊情况的研究来判断一般规律,从而“小题小做”或“小题巧做”.
2.当题目的已知条件中含有某些不确定的量时,可针对题目中变化的不定量选取一些符合条件的特殊值(或特殊函数、特殊角、特殊数列、特殊图形、图形特殊位置、特殊点、特殊方程、特殊模型等)进行处理,从而得出探求的结论.这样可大大地简化推理、论证的过程.
A.a>b>c B.b>c>a
C.b>a>c D.c>a>b
(2) 如图所示,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,
(2)所求的问题是个定值问题,“在△ABC中”和在特殊△ABC中所求的值相等,所以将所给条件“在△ABC中”特殊化为“在等边三角形ABC中”.如图所示.
考向3排除法(针对选择题)
例3(1)(2022·河南名校联盟一模)已知α是第二象限角,则( )
A.cos α>0 B.sin α<0
C.sin 2α<0 D.tan α>0
(2)(2020·全国Ⅱ·文5)已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是( )
A.a+2b B.2a+b
C.a-2b D.2a-b
(3)函数f(x)= (其中e为自然对数的底数)的图象大致为( )
答案 (1)C (2)D (3)A
解析 (1)因为α是第二象限角,所以cos α<0,sin α>0,tan α<0,故选项ABC都错,故选C.
对于D,(2a-b)·b=2a·b-b2=0,故2a-b与b垂直.故选D.
规律方法
数学选择题的解题本质就是去伪存真,舍弃不符合题目要求的选项,找到符合题意的正确结论.排除法(又叫筛选法)就是通过观察分析或推理运算各项提供的信息或通过特例,对于不符合题意的选项逐一剔除,从而获得正确的结论.
对点练3(1)(2020·浙江·4)函数y=xcos x+sin x在区间[-π,π]上的图象可能是( )
(2)(2022·山西长治模拟预测)若函数f(x)对定义域中的任意取值x都满足f(x+2)=f(x),则f(x)可以是( )
A.f(x)=(x-1)2 B.f(x)=|x-2|
答案 (1)A (2)D
考向4解析法
(2)(2022·山东济宁一模)在边长为6的菱形ABCD中,A= ,现将△ABD沿BD折起,当三棱锥A-BCD的体积最大时,三棱锥A-BCD的外接球的表面积为 .
答案 (1)B (2)60π
解析 (1)以O为坐标原点,建立平面直角坐标系如图所示,过点A作x轴的垂
(2)如图所示,取BD的中点O为坐标原点,直线OC为x轴,直线BD为y轴,过点O垂直于平面BCD的直线为z轴,建立空间直角坐标系,当点A在z轴上时,
是OA上靠近点O的三等分点,取点F是OC上靠近点O的三等分点,则点E,F分别是等边三角形ABD与等边三角形CBD的中心.分别过点E,F作直线垂直于平面ABD与平面CBD,设这两条直线交于点G,则点G就是三棱锥A-BCD
所以三棱锥A-BCD的外接球的表面积为4π×15=60π.
规律方法
解析法又称坐标法,是解析几何中最基本的研究方法,它是在平面直角坐标系的基础上,把几何问题转化为代数问题,通过代数运算研究几何图形性质的方法.
答案 (1)A (2)B
考向5等价转化法
例5(1)已知直线x+y+m=0与圆x2+y2=2交于不同的两点A,B,O是坐标原点,
答案 (1)D (2)A
(2)函数f(x)过点(1,0),所以函数f(x)有且只有一个零点 函数y=-2x+a(x≤0)没有零点 函数y=2x(x≤0)与直线y=a无公共点,可得a≤0或a>1.又{a|a<0} {a|a≤0或a>1},故选A.
规律方法
等价转化法就是把未知的问题转化到在已有知识范围内可解的问题的一种重要的思想方法.通过不断地转化,可把不熟悉、不规范、复杂的问题转化为熟悉、规范、简单的问题.
对点练5(1)一给定函数y=f(x)的图象在下列图中,并且对任意a1∈(0,1),由关系式an+1=f(an)得到的数列{an},满足an+1
答案 (1)B (2)C
解析 (1)对任意a1∈(0,1),∵an+1=f(an),又an+1
又∠DAB=180°-∠CAB=120°,
故∠ADB= (180°-120°)=30°,
∴∠ADB+∠DCB=90°,即∠DBC=90°,故CB⊥DB.∵PB=4,PC=5,BC=3,
∴PC2=PB2+BC2,∴CB⊥PB.
∵DB∩PB=B,DB 平面PBD,PB 平面PBD,∴CB⊥平面PBD.
考向6构造法
例6(1)(2022·江苏南通第一次调研)已知α,β均为锐角,且α+β- >sin β-cos α,则( )
A.sin α>sin β
B.cos α>cos β
C.cos α>sin β
D.sin α>cos β
(2)已知a>b>e,其中e是自然对数的底数,则ab与ba的大小关系为
ab ba(从“>”“=”“<”中选择一个).
答案 (1)D (2)<
规律方法
利用已知条件和结论的特殊性构造出新的数学模型,从而简化推理与计算过程,使较复杂的数学问题得到简捷的解决.构造法是建立在观察联想、分析综合的基础之上的,从曾经遇到过的类似问题中寻找灵感,构造出相应的函数、概率、几何等具体的数学模型,使问题得到快速解决.
A.c
同课章节目录
