2023届高考二轮总复习课件(适用于新高考新教材) 数学 7.概率与统计(共15张PPT)
文档属性
| 名称 | 2023届高考二轮总复习课件(适用于新高考新教材) 数学 7.概率与统计(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 294.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 17:34:37 | ||
图片预览





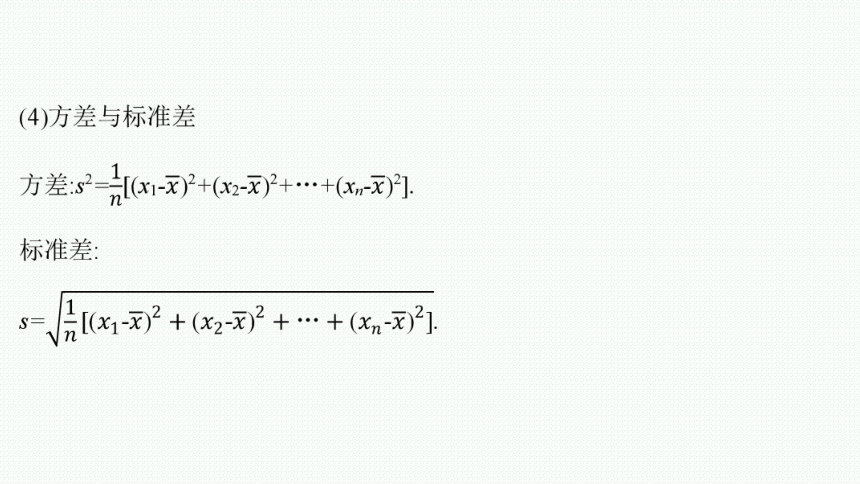

文档简介
(共15张PPT)
7.概率与统计
下篇
1.概率的计算公式
(2)互斥事件的概率计算公式P(A∪B)=P(A)+P(B).
(5)相互独立事件同时发生的概率
①计算公式:P(AB)=P(A)P(B).
②公式的推广:若事件A1,A2,…,An相互独立,则P(A1A2…An)=P(A1)P(A2)…P(An).
(6)概率的乘法公式
对任意两个事件A与B,若P(A)>0,则P(BA)=P(A)P(B|A).
(7)全概率公式
一般地,设A1,A2,…,An是一组两两互斥的事件,且A1∪A2∪…∪An=Ω,P(Ai)>0,i=1,2,…,n,则对任意事件B Ω,
有P(B)= P(Ai)P(B|Ai).
(8)贝叶斯公式
设A1,A2,…,An是一组两两互斥的事件,A1∪A2∪…∪An=Ω,P(Ai)>0,i=1,2,…,
2.统计中四个数据特征
(1)众数:在样本数据中,出现次数最多的那个数据.
(2)中位数:在样本数据中,将数据按大小排列,位于最中间的数据.如果数据的个数为偶数,就取中间两个数据的平均数作为中位数.
3.离散型随机变量
(1)离散型随机变量的分布列的两个性质
①pi≥0(i=1,2,…,n);②p1+p2+…+pn=1.
(2)期望公式E(X)=x1p1+x2p2+…+xnpn.
(3)期望的性质
①E(aX+b)=aE(X)+b;
②若X~B(n,p),则E(X)=np;
③若X服从两点分布,则E(X)=p.
(4)方差公式
D(X)=[x1-E(X)]2·p1+[x2-E(X)]2·p2+…+[xn-E(X)]2·pn,标准差为 .
(5)方差的性质
①D(aX+b)=a2D(X);
②若X~B(n,p),则D(X)=np(1-p);
③若X服从两点分布,则D(X)=p(1-p).
(6)独立事件同时发生的概率计算公式:P(AB)=P(A)P(B).
4.一元线性回归模型
设满足一元线性回归模型的两个变量的n对样本数据为(x1,y1),(x2,y2),…,(xn,yn),
当a,b的取值为
5.样本相关系数
(1)计算公式:
(2)样本相关系数的意义
样本相关系数r是一个描述成对样本数据的数字特征,它的正负性可以反映成对样本数据的变化特征.
|r|的大小反映了两个变量相关的程度,具体如下:
①r的正负性:当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.
②r的绝对值:当|r|越接近于1时,成对样本数据的线性相关程度越强;当|r|越接近于0时,成对样本数据线性相关程度越弱.
6.独立性检验
利用随机变量χ2= 来判断“两个分类变量是否独立”的方法称为独立性检验.
基于小概率值α的检验规则是:
当χ2≥xα时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过α;
当χ27.正态分布
如果随机变量X服从正态分布,则记为X~N(μ,σ2).满足正态分布的三个基本概率的值是:①P(μ-σ≤X≤μ+σ)≈0.682 7;②P(μ-2σ≤X≤μ+2σ)≈0.954 5;③P(μ-3σ≤X≤μ+3σ)≈0.997 3.
易错提醒
1.应用互斥事件的概率加法公式,一定要注意首先确定各事件是否彼此互斥,然后求出各事件分别发生的概率,再求和.
2.正确区别互斥事件与对立事件的关系:对立事件是互斥事件,是互斥事件中的特殊情况,但互斥事件不一定是对立事件,“互斥”是“对立”的必要不充分条件.
3.易把频率分布直方图纵轴的几何意义当成频率,导致样本数据的频率求错.
4.要注意概率P(A|B)与P(AB)的区别:
(1)在P(A|B)中,事件A,B发生有时间上的差异,B先A后;在P(AB)中,事件A,B同时发生.
(2)样本空间不同,在P(A|B)中,事件B成为样本空间;在P(AB)中,样本空间仍为Ω,因而有P(A|B)≥P(AB).
5.易忘判定随机变量是否服从二项分布,盲目使用二项分布的期望和方差公式计算致误.
7.概率与统计
下篇
1.概率的计算公式
(2)互斥事件的概率计算公式P(A∪B)=P(A)+P(B).
(5)相互独立事件同时发生的概率
①计算公式:P(AB)=P(A)P(B).
②公式的推广:若事件A1,A2,…,An相互独立,则P(A1A2…An)=P(A1)P(A2)…P(An).
(6)概率的乘法公式
对任意两个事件A与B,若P(A)>0,则P(BA)=P(A)P(B|A).
(7)全概率公式
一般地,设A1,A2,…,An是一组两两互斥的事件,且A1∪A2∪…∪An=Ω,P(Ai)>0,i=1,2,…,n,则对任意事件B Ω,
有P(B)= P(Ai)P(B|Ai).
(8)贝叶斯公式
设A1,A2,…,An是一组两两互斥的事件,A1∪A2∪…∪An=Ω,P(Ai)>0,i=1,2,…,
2.统计中四个数据特征
(1)众数:在样本数据中,出现次数最多的那个数据.
(2)中位数:在样本数据中,将数据按大小排列,位于最中间的数据.如果数据的个数为偶数,就取中间两个数据的平均数作为中位数.
3.离散型随机变量
(1)离散型随机变量的分布列的两个性质
①pi≥0(i=1,2,…,n);②p1+p2+…+pn=1.
(2)期望公式E(X)=x1p1+x2p2+…+xnpn.
(3)期望的性质
①E(aX+b)=aE(X)+b;
②若X~B(n,p),则E(X)=np;
③若X服从两点分布,则E(X)=p.
(4)方差公式
D(X)=[x1-E(X)]2·p1+[x2-E(X)]2·p2+…+[xn-E(X)]2·pn,标准差为 .
(5)方差的性质
①D(aX+b)=a2D(X);
②若X~B(n,p),则D(X)=np(1-p);
③若X服从两点分布,则D(X)=p(1-p).
(6)独立事件同时发生的概率计算公式:P(AB)=P(A)P(B).
4.一元线性回归模型
设满足一元线性回归模型的两个变量的n对样本数据为(x1,y1),(x2,y2),…,(xn,yn),
当a,b的取值为
5.样本相关系数
(1)计算公式:
(2)样本相关系数的意义
样本相关系数r是一个描述成对样本数据的数字特征,它的正负性可以反映成对样本数据的变化特征.
|r|的大小反映了两个变量相关的程度,具体如下:
①r的正负性:当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.
②r的绝对值:当|r|越接近于1时,成对样本数据的线性相关程度越强;当|r|越接近于0时,成对样本数据线性相关程度越弱.
6.独立性检验
利用随机变量χ2= 来判断“两个分类变量是否独立”的方法称为独立性检验.
基于小概率值α的检验规则是:
当χ2≥xα时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过α;
当χ2
如果随机变量X服从正态分布,则记为X~N(μ,σ2).满足正态分布的三个基本概率的值是:①P(μ-σ≤X≤μ+σ)≈0.682 7;②P(μ-2σ≤X≤μ+2σ)≈0.954 5;③P(μ-3σ≤X≤μ+3σ)≈0.997 3.
易错提醒
1.应用互斥事件的概率加法公式,一定要注意首先确定各事件是否彼此互斥,然后求出各事件分别发生的概率,再求和.
2.正确区别互斥事件与对立事件的关系:对立事件是互斥事件,是互斥事件中的特殊情况,但互斥事件不一定是对立事件,“互斥”是“对立”的必要不充分条件.
3.易把频率分布直方图纵轴的几何意义当成频率,导致样本数据的频率求错.
4.要注意概率P(A|B)与P(AB)的区别:
(1)在P(A|B)中,事件A,B发生有时间上的差异,B先A后;在P(AB)中,事件A,B同时发生.
(2)样本空间不同,在P(A|B)中,事件B成为样本空间;在P(AB)中,样本空间仍为Ω,因而有P(A|B)≥P(AB).
5.易忘判定随机变量是否服从二项分布,盲目使用二项分布的期望和方差公式计算致误.
同课章节目录
