2023届高考二轮总复习课件(适用于新高考新教材) 数学 4.三角函数、三角恒等变换与解三角形 课件(共17张PPT)
文档属性
| 名称 | 2023届高考二轮总复习课件(适用于新高考新教材) 数学 4.三角函数、三角恒等变换与解三角形 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 17:34:57 | ||
图片预览





文档简介
(共17张PPT)
4.三角函数、三角恒等变换与解三角形
下篇
1.终边相同的角
与角α终边相同的角,连同角α在内的集合:{β|β=k·360°+α,k∈Z}.
2.几种特殊位置角的集合表示
角α终边的位置 角α的集合表示
在x轴的非负半轴上 {α|α=k·360°,k∈Z}
在x轴的非正半轴上 {α|α=k·360°+180°,k∈Z}
在y轴的非负半轴上 {α|α=k·360°+90°,k∈Z}
在y轴的非正半轴上 {α|α=k·360°+270°,k∈Z}
在x轴上 {α|α=k·180°,k∈Z}
在y轴上 {α|α=k·180°+90°,k∈Z}
在坐标轴上 {α|α=k·90°,k∈Z}
3.弧度制
(1)弧度的定义
把长度等于半径长的弧所对的圆心角叫做1弧度的角,用符号“rad”表示,读作弧度.
①任一已知角α的弧度数的绝对值|α|= ,其中l为以角α作为圆心角时所对圆弧的长,r为圆的半径.
②这种用“弧度”作单位来度量角的单位制叫做弧度制.
③比值 与所取的圆的半径大小无关,而仅与角的大小有关.
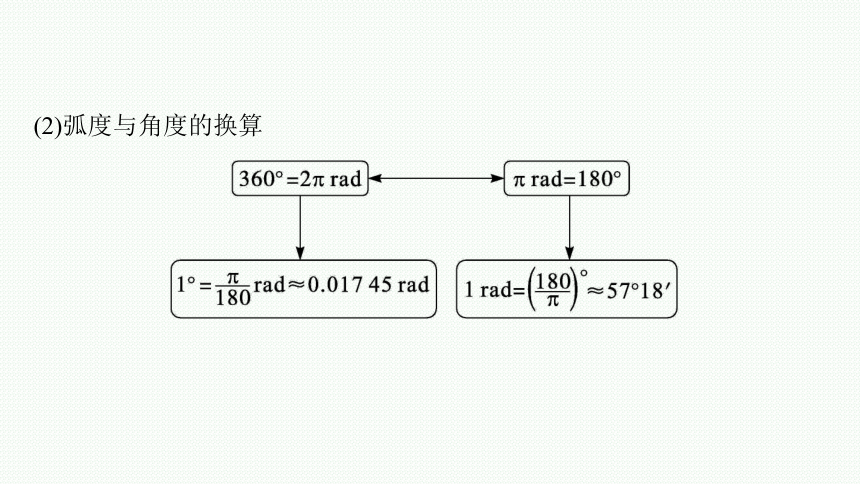
(2)弧度与角度的换算
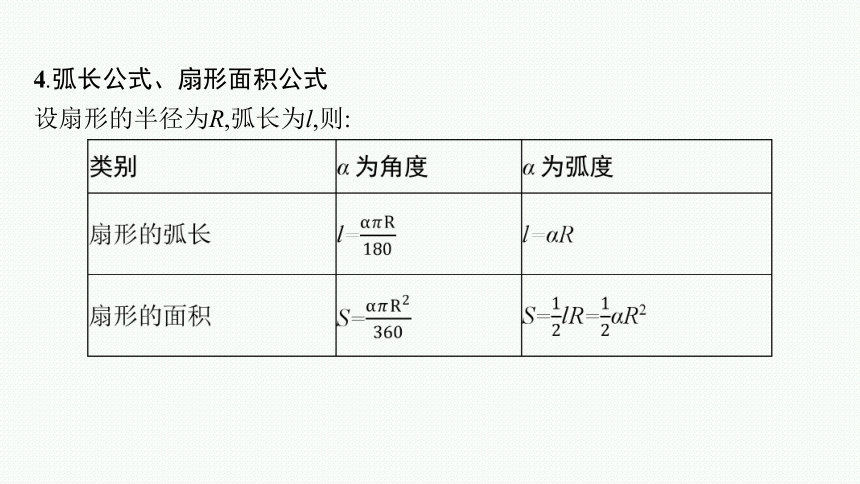
4.弧长公式、扇形面积公式
设扇形的半径为R,弧长为l,则:
5.任意角的三角函数定义
设α是一个任意角.角α的终边上任意一点P的坐标是(x,y),它与原点的距离
6.同角三角函数的基本关系式
7.诱导公式
组数 一 二 三 四 五 六
角 2kπ+α (k∈Z) π+α -α π-α -α +α
正弦 sin α -sin α -sin α sin α cos α cos α
余弦 cos α -cos α cos α -cos α sin α -sin α
正切 tan α tan α -tan α -tan α — —
口诀 函数名不变,符号看象限 函数名改变, 符号看象限
8.三种三角函数的性质
9.函数y=Asin(ωx+φ)(ω>0,A>0)的图象
(1)“五点法”作图
(2)由三角函数的图象确定解析式时,一般利用五点中的零点或最值点作为解题突破口.
(3)图象变换
10.三角恒等变换公式
(1)两角和与差的余弦公式
名称 公式 简记符号
两角和的余弦 cos(α+β)=cos αcos β-sin αsin β C(α+β)
两角差的余弦 cos(α-β)=cos αcos β+sin αsin β C(α-β)
(2)两角和与差的正弦公式
名称 公式 简记符号
两角和的正弦 sin(α+β)=sin αcos β+cos αsin β S(α+β)
两角差的正弦 sin(α-β)=sin αcos β-cos αsin β S(α-β)
(3)两角和与差的正切公式
(4)二倍角的正弦、余弦、正切公式
cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α,
sin 2α=2sin αcos α,
11.三角函数恒等变换“四大策略”
(1)常值代换:特别是“1”的代换,1=sin2θ+cos2θ=tan 45°等.
(2)降次与升次:正用二倍角公式升次,逆用二倍角公式降次.
(3)弦、切互化:一般是切化弦.
12.正弦定理及其变形
13.余弦定理及其推论、变形
a2=b2+c2-2bccos A,b2=a2+c2-2accos B,c2=a2+b2-2abcos C.
易错提醒
1.利用同角三角函数的平方关系式求值时,不要忽视角的范围,要先判断函数值的符号.
2.在求三角函数的值域(或最值)时,不要忽略x的取值范围.
3.求函数f(x)=Asin(ωx+φ)的单调区间时,要注意A与ω的符号,当ω<0时,需把ω的符号化为正值后求解.
4.三角函数图象变换中,注意由y=sin ωx的图象变换得到y=sin(ωx+φ)的图
5.在已知两边和其中一边的对角利用正弦定理求解时,要注意检验解是否满足“大边对大角”,避免增解.
4.三角函数、三角恒等变换与解三角形
下篇
1.终边相同的角
与角α终边相同的角,连同角α在内的集合:{β|β=k·360°+α,k∈Z}.
2.几种特殊位置角的集合表示
角α终边的位置 角α的集合表示
在x轴的非负半轴上 {α|α=k·360°,k∈Z}
在x轴的非正半轴上 {α|α=k·360°+180°,k∈Z}
在y轴的非负半轴上 {α|α=k·360°+90°,k∈Z}
在y轴的非正半轴上 {α|α=k·360°+270°,k∈Z}
在x轴上 {α|α=k·180°,k∈Z}
在y轴上 {α|α=k·180°+90°,k∈Z}
在坐标轴上 {α|α=k·90°,k∈Z}
3.弧度制
(1)弧度的定义
把长度等于半径长的弧所对的圆心角叫做1弧度的角,用符号“rad”表示,读作弧度.
①任一已知角α的弧度数的绝对值|α|= ,其中l为以角α作为圆心角时所对圆弧的长,r为圆的半径.
②这种用“弧度”作单位来度量角的单位制叫做弧度制.
③比值 与所取的圆的半径大小无关,而仅与角的大小有关.
(2)弧度与角度的换算
4.弧长公式、扇形面积公式
设扇形的半径为R,弧长为l,则:
5.任意角的三角函数定义
设α是一个任意角.角α的终边上任意一点P的坐标是(x,y),它与原点的距离
6.同角三角函数的基本关系式
7.诱导公式
组数 一 二 三 四 五 六
角 2kπ+α (k∈Z) π+α -α π-α -α +α
正弦 sin α -sin α -sin α sin α cos α cos α
余弦 cos α -cos α cos α -cos α sin α -sin α
正切 tan α tan α -tan α -tan α — —
口诀 函数名不变,符号看象限 函数名改变, 符号看象限
8.三种三角函数的性质
9.函数y=Asin(ωx+φ)(ω>0,A>0)的图象
(1)“五点法”作图
(2)由三角函数的图象确定解析式时,一般利用五点中的零点或最值点作为解题突破口.
(3)图象变换
10.三角恒等变换公式
(1)两角和与差的余弦公式
名称 公式 简记符号
两角和的余弦 cos(α+β)=cos αcos β-sin αsin β C(α+β)
两角差的余弦 cos(α-β)=cos αcos β+sin αsin β C(α-β)
(2)两角和与差的正弦公式
名称 公式 简记符号
两角和的正弦 sin(α+β)=sin αcos β+cos αsin β S(α+β)
两角差的正弦 sin(α-β)=sin αcos β-cos αsin β S(α-β)
(3)两角和与差的正切公式
(4)二倍角的正弦、余弦、正切公式
cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α,
sin 2α=2sin αcos α,
11.三角函数恒等变换“四大策略”
(1)常值代换:特别是“1”的代换,1=sin2θ+cos2θ=tan 45°等.
(2)降次与升次:正用二倍角公式升次,逆用二倍角公式降次.
(3)弦、切互化:一般是切化弦.
12.正弦定理及其变形
13.余弦定理及其推论、变形
a2=b2+c2-2bccos A,b2=a2+c2-2accos B,c2=a2+b2-2abcos C.
易错提醒
1.利用同角三角函数的平方关系式求值时,不要忽视角的范围,要先判断函数值的符号.
2.在求三角函数的值域(或最值)时,不要忽略x的取值范围.
3.求函数f(x)=Asin(ωx+φ)的单调区间时,要注意A与ω的符号,当ω<0时,需把ω的符号化为正值后求解.
4.三角函数图象变换中,注意由y=sin ωx的图象变换得到y=sin(ωx+φ)的图
5.在已知两边和其中一边的对角利用正弦定理求解时,要注意检验解是否满足“大边对大角”,避免增解.
同课章节目录
