余弦定理[下学期]

课件13张PPT。1余弦定理2 什么叫做正弦定理，用正弦定理解三角形必须已知哪些量？复习 在一个三角形中，各边和它所对角的正弦的比相等. 即：正弦定理: 用正弦定理解三角形，必须已知三角形的两角和一边或者已知两边和其中一边的对角．3 1. 在?ABC中，已知a = 1，b = ，A = 30?，解此三角形．练习B = 60?，C = 90?，c = 2;
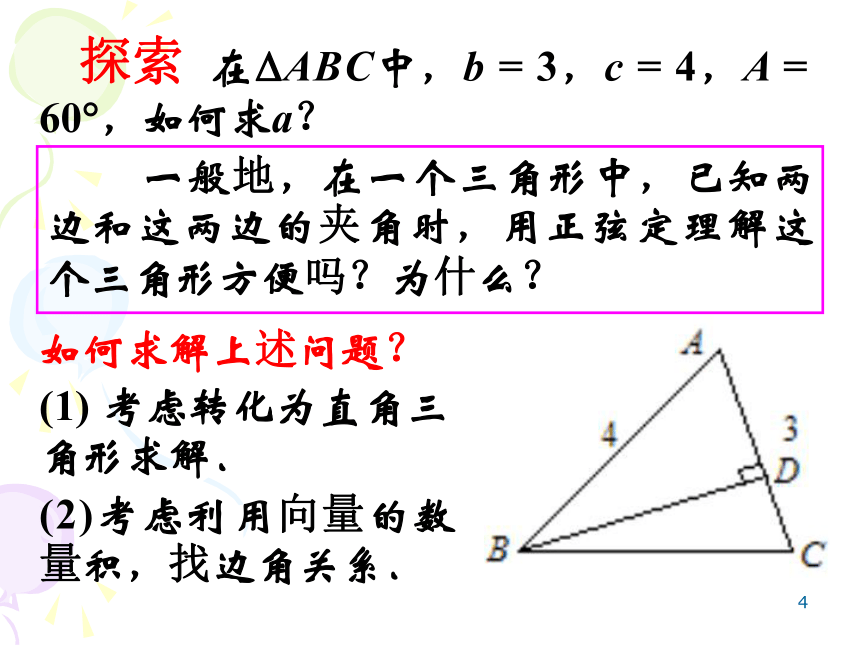
或B = 120?， C = 30?，c = 1．等腰三角形(B = C)． 2. 在?ABC中，2bcosC = a，判断此三角形的形状．4 在?ABC中，b = 3，c = 4，A = 60?，如何求a？探索 一般地，在一个三角形中，已知两边和这两边的夹角时，用正弦定理解这个三角形方便吗？为什么？如何求解上述问题？(1) 考虑转化为直角三角形求解．(2)考虑利用向量的数量积，找边角关系．5 三角形任何一边的平方等于其他两边的平方和减去这两边与它们夹角余弦的积的二倍．即:余弦定理:a2 = b2 + c2 ? 2bccosA; 利用余弦定理可以解决怎样的三角形问题？b2 = c2 + a2 ? 2cacosB;c2 = a2 + b2 ? 2abcosC．① 已知三角形三边求角；② 已知两边和它们的夹角，求第三边.6余弦定理的变形:由a2 = b2 + c2 ? 2bccosA;b2 = c2 + a2 ? 2cacosB;c2 = a2 + b2 ? 2abcosC可得:7 例1 在?ABC中，已知a = 7，b = 10，c = 6，求A、B和C(精确到1?)．分析: 已知三边求角, 联想余弦定理求解.解: [或∵sinC = ≈ 0.5954，
∴ C ≈ 36°或144°(舍)]8 例1 在?ABC中，已知a = 7，b = 10，c = 6，求A、B和C(精确到1?)．思考: (1) 判定例1中?ABC的形状.∴ ?ABC为钝角三角形.思考: (2) 求例1中?ABC的面积.由此得: B ? (90?，180?) ? b2 > a2 + c2. 9 例3 已知三角形的一个角为60?，面积为10 cm2，周长为20cm，求此三角形的各边长．　 例2 ΔABC的三个顶点坐标分别为A(6，5)、B(– 2，8)、C(4，1)，求cosA． 分析：此题所给的条件除一个角外，面积、周长都不是构成三角形的基本元素，但是都与三角形的边长有关系，故可以设出边长，利用所给条件建立方程，这样由于边长为三个未知数，所以需寻求三个方程.分别为5cm，7cm，8cm.10注意: (1) 在建立方程的过程中，既要注意由余弦定理可以建立方程，也要注意含有正弦形式的面积公式的应用． (2) 由条件得到的是一个三元二次方程组，要注意体会其求解的方法和思路，以提高自己的解方程及运算能力．11小结：3. 由余弦定理可知，?ABC中：1. 余弦定理适用于任何三角形． 2. 余弦定理的作用：已知两边及两边夹角求第三边；已知三边求三角；判断三角形形状．A > 90? ? a2 > b2 + c2; A = 90? ? a2 = b2 + c2; A < 90? ? a2 < b2 + c2; 12 1. 已知?ABC中，a = 20，b = 29，c = 21，求B． 2. 若锐角?ABC中，b = 8，c = 3，
sinA = ，求a并判定三角形的形状.巩固练习：B = 90?a = 8，?ABC为等腰三角形.13在△ABC中，求证：
(a2 ? b2 ? c2)tanA + (a2 ? b2 + c2)tanB = 0.课外思考题：