专题一 集合 课件——2023届高三数学二轮专题复习 课件(共29张PPT)
文档属性
| 名称 | 专题一 集合 课件——2023届高三数学二轮专题复习 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 704.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-12 14:17:53 | ||
图片预览






文档简介
(共29张PPT)
专题一 集合
2023高考一轮复习
1.了解集合的含义、元素与集合的属于关系.能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.
2.理解集合之间包含与相等的含义,能识别给定集合的子集.在具体情境中,了解全集与空集的含义.
3.理解两个集合的并集与交集的含义,会求两个集合的并集与交集.理解在给定集合中一个子集的补集的含义,会求给定子集的补集.能使用韦恩(Venn)图表达集合的基本关系与基本运算.
学习目标
考情分析:集合的交、并、补运算及两集合间的包含关系是考查的重点,在集合的运算中经常与不等式、函数相结合,解题时常用到数轴和韦恩(Venn)图,题型以选择题为主.
学科素养:通过集合间的基本关系和基本运算考查数学抽象及数学运算的核心素养.
考向预测
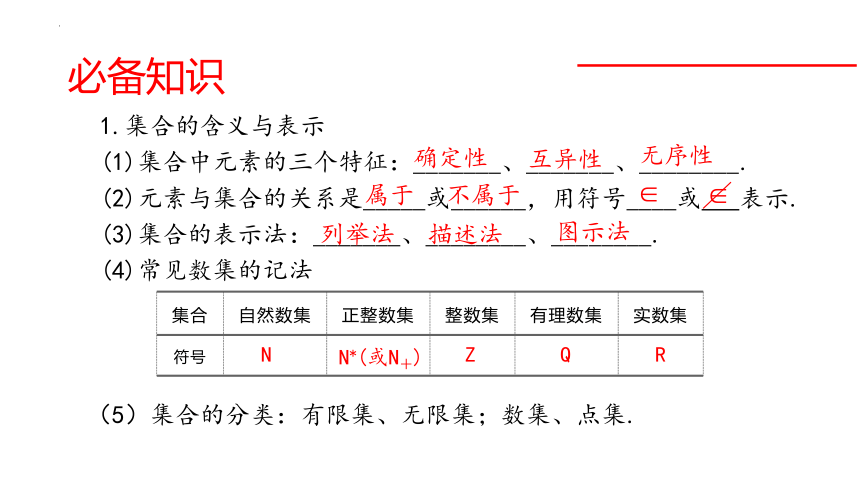
1.集合的含义与表示
(1)集合中元素的三个特征:_______、_______、________.
(2)元素与集合的关系是_____或______,用符号____或 表示.
(3)集合的表示法:_______、________、________.
(4)常见数集的记法
(5)集合的分类:有限集、无限集;数集、点集.
确定性
互异性
无序性
属于
不属于
∈
列举法
描述法
图示法
集合 自然数集 正整数集 整数集 有理数集 实数集
符号
N
N*(或N+)
Z
Q
R
必备知识
∈
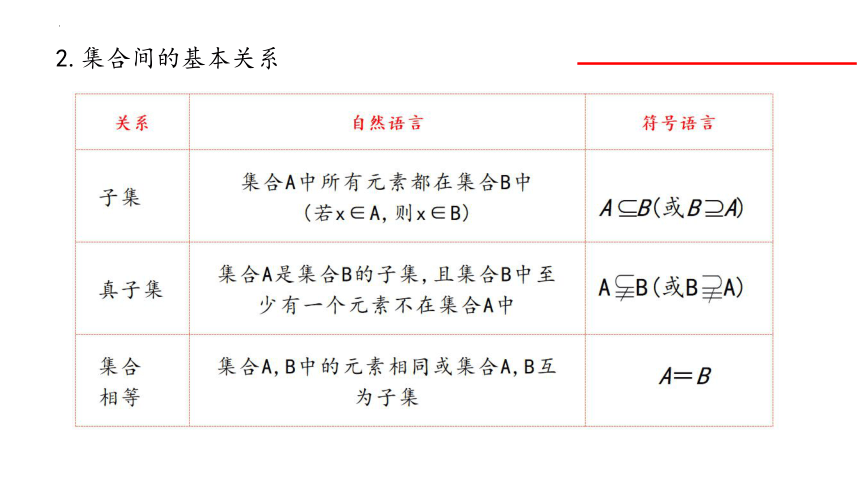
2.集合间的基本关系
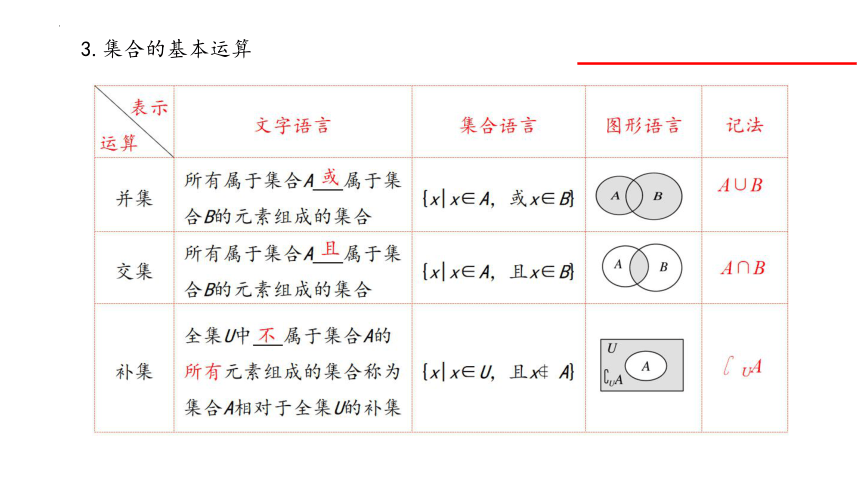
3.集合的基本运算
常用结论
4.空集是任何集合的子集,是任何非空集合的真子集.
考点一 集合的含义与表示
1、已知集合A={x∈Z|x2+2x-8<0},B={x2|x∈A},则 B中元素个数为( )
A.4 B.5
C.6 D.7
A
考点一 集合的含义与表示
2.若集合P={x∈N|x≤},a=2,则( )
A.a∈P B.{a}∈P
C.{a} P D.a P
D
考点一 集合的含义与表示
3.若集合A={x∈R|ax2-3x+2=0}中只有一个元素,则a=( )
A. B.
C.0 D.0或
D
已知集合A={m+2,2m2+m},若3∈A,求m的值.
易错点 忽视集合元素的互异性
练习:已知 ,若 =
则
易错点 数集和点集的区分
B
C
考点二 集合间的基本关系
1.已知集合A满足{0,1} A {0,1,2,3},则集合A的个数为( )
A.1 B.2 C.3 D.4
C
考点二 集合间的基本关系
2.已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B A,则实数m的取值范围为________
练习:已知集合A={x|-2≤x≤7},B={x|m+1考点二 集合间的基本关系
3.已知集合
C
驻马店市第二高级中学
练习:已知集合 ,则
B
考点三 集合的运算
B
考点三 集合的运算
D
3.已知全集U=R,集合A={x|x2-4<0,x∈Z},集合B={x|x2-2x-3=0},则图中阴影部分表示的集合是( )
A.{0,1,3} B.{-2,0,1,2,3}
C.{0,-1,-3} D.{-1,0,1,3}
考点三 集合的运算
A
考点四 补集思想的应用
练习:已知集合
若三个集合至少有一个不是空集,则实数a的取值范围是
考点五 集合新定义问题
1.如果集合A满足若 ,那么就称集合A为“对称集合”.已知集合 是对称集合,则A=
{-6,0,6}
C
知识体系
1.设U={1,2,3},M,N是U的子集,若M={1,3},则称(M,N)为一个“理想配集”,则符合此条件的“理想配集”的个数(规定(M,N)与(N,M)不同)为________.
2.已知集合A={x|x2-4x+3<0},B={x|x>m},若A={x|x>1},则( )
A.m≥1 B.1≤m<3
C.13.已知集合A={x|x2-x-2<0},则 RA=( )
A.{x|-1C.{x|x<-1或x>2} D.{x|x≤-1或x≥2}
练习
谢谢观看
专题一 集合
2023高考一轮复习
1.了解集合的含义、元素与集合的属于关系.能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.
2.理解集合之间包含与相等的含义,能识别给定集合的子集.在具体情境中,了解全集与空集的含义.
3.理解两个集合的并集与交集的含义,会求两个集合的并集与交集.理解在给定集合中一个子集的补集的含义,会求给定子集的补集.能使用韦恩(Venn)图表达集合的基本关系与基本运算.
学习目标
考情分析:集合的交、并、补运算及两集合间的包含关系是考查的重点,在集合的运算中经常与不等式、函数相结合,解题时常用到数轴和韦恩(Venn)图,题型以选择题为主.
学科素养:通过集合间的基本关系和基本运算考查数学抽象及数学运算的核心素养.
考向预测
1.集合的含义与表示
(1)集合中元素的三个特征:_______、_______、________.
(2)元素与集合的关系是_____或______,用符号____或 表示.
(3)集合的表示法:_______、________、________.
(4)常见数集的记法
(5)集合的分类:有限集、无限集;数集、点集.
确定性
互异性
无序性
属于
不属于
∈
列举法
描述法
图示法
集合 自然数集 正整数集 整数集 有理数集 实数集
符号
N
N*(或N+)
Z
Q
R
必备知识
∈
2.集合间的基本关系
3.集合的基本运算
常用结论
4.空集是任何集合的子集,是任何非空集合的真子集.
考点一 集合的含义与表示
1、已知集合A={x∈Z|x2+2x-8<0},B={x2|x∈A},则 B中元素个数为( )
A.4 B.5
C.6 D.7
A
考点一 集合的含义与表示
2.若集合P={x∈N|x≤},a=2,则( )
A.a∈P B.{a}∈P
C.{a} P D.a P
D
考点一 集合的含义与表示
3.若集合A={x∈R|ax2-3x+2=0}中只有一个元素,则a=( )
A. B.
C.0 D.0或
D
已知集合A={m+2,2m2+m},若3∈A,求m的值.
易错点 忽视集合元素的互异性
练习:已知 ,若 =
则
易错点 数集和点集的区分
B
C
考点二 集合间的基本关系
1.已知集合A满足{0,1} A {0,1,2,3},则集合A的个数为( )
A.1 B.2 C.3 D.4
C
考点二 集合间的基本关系
2.已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B A,则实数m的取值范围为________
练习:已知集合A={x|-2≤x≤7},B={x|m+1
3.已知集合
C
驻马店市第二高级中学
练习:已知集合 ,则
B
考点三 集合的运算
B
考点三 集合的运算
D
3.已知全集U=R,集合A={x|x2-4<0,x∈Z},集合B={x|x2-2x-3=0},则图中阴影部分表示的集合是( )
A.{0,1,3} B.{-2,0,1,2,3}
C.{0,-1,-3} D.{-1,0,1,3}
考点三 集合的运算
A
考点四 补集思想的应用
练习:已知集合
若三个集合至少有一个不是空集,则实数a的取值范围是
考点五 集合新定义问题
1.如果集合A满足若 ,那么就称集合A为“对称集合”.已知集合 是对称集合,则A=
{-6,0,6}
C
知识体系
1.设U={1,2,3},M,N是U的子集,若M={1,3},则称(M,N)为一个“理想配集”,则符合此条件的“理想配集”的个数(规定(M,N)与(N,M)不同)为________.
2.已知集合A={x|x2-4x+3<0},B={x|x>m},若A={x|x>1},则( )
A.m≥1 B.1≤m<3
C.1
A.{x|-1
练习
谢谢观看
同课章节目录
