北师大版四年级下册数学2.3 探索与发现:三角形内角和(课件)(共15张PPT)
文档属性
| 名称 | 北师大版四年级下册数学2.3 探索与发现:三角形内角和(课件)(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 809.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 15:23:11 | ||
图片预览





文档简介
(共15张PPT)
第3课时 探索与发现:三角形内角和
第二单元 认识三角形和四边形
1.掌握三角形的内角和是180°。
2.能根据两个已知角的度数求出第三个角的度数。
重点:掌握三角形的内角和是180°。
难点:能根据两个已知角的度数求出第三个角的度数。
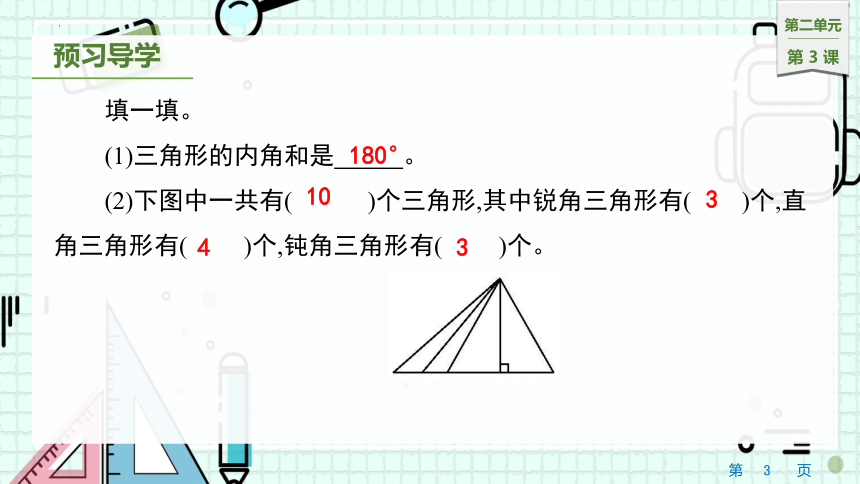
填一填。
(1)三角形的内角和是 。
(2)下图中一共有( )个三角形,其中锐角三角形有( )个,直角三角形有( )个,钝角三角形有( )个。
180°
3
4
3
10
1.课前要让学生多准备各种三角形,通过动手操作使学生明白三角形内角和的含义。
2.通过图形的变形,使学生灵活运用三角形内角和去解决生活中的问题。
任务驱动
1.什么是三角形的内角 什么是三角形的内角和
三角形中相邻两边组成的角叫作三角形的内角。
三角形三个内角的和叫作三角形的内角和。
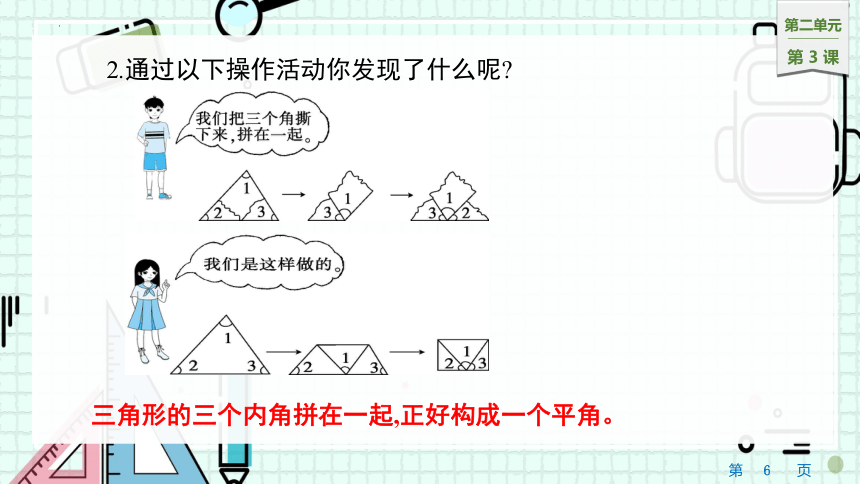
2.通过以下操作活动你发现了什么呢
三角形的三个内角拼在一起,正好构成一个平角。
3.你能画一个有两个内角是直角的三角形吗
4.直角三角形中两个锐角的和是多少度
不能,一个三角形最多只能有一个直角。
90°
5.一个三角形至少有几个锐角 为什么
两个锐角。如果只有一个锐角,那么就会有两个直角或钝角,这时三角形的内角和会超过180°。
6.等腰三角形和等边三角形的角有什么特点
等腰三角形的两个底角相等。
等边三角形的三个角都相等,都是60°。
归纳总结
1.三角形的内角和是180°。
2.等腰三角形的底角相等。等边三角形的三个角都相等,它们的度数都是60°。
1.填一填。
(1)在直角三角形中,一个锐角是54°,另一个锐角是( )。
(2)等边三角形每个内角都是( )。
(3)在一个三角形中,两个内角的度数分别为30°和75°,则另一个内角的度数为( )。这是一个( )三角形,也是一个( )三角形。
36°
锐角
等腰
75°
60°
2.根据条件算出角的度数。( 综合类作业)
(1)如图,已知∠4=143°,∠1=72°,求∠2和∠3的度数。
∠2=180°-143°=37°
∠3=180°-72°-37°=71°
(2)一个等腰三角形,它的一个底角是40°,它的顶角是多少度
180°-40°-40°=100°
3.下图是两块三角形木板破碎后留下的碎片,你知道它们原来的形状分别是什么三角形吗 ( 实践类作业)
先用量角器量出两块三角形木板碎片上剩余2个角的度数。
(1)180°-45°-60°=75°
答:第一块木板原来的形状是锐角三角形。
(2)180°-60°-30°=90°
答:第二块木板原来的形状是直角三角形。
END
感谢观看 下节课再会
第3课时 探索与发现:三角形内角和
第二单元 认识三角形和四边形
1.掌握三角形的内角和是180°。
2.能根据两个已知角的度数求出第三个角的度数。
重点:掌握三角形的内角和是180°。
难点:能根据两个已知角的度数求出第三个角的度数。
填一填。
(1)三角形的内角和是 。
(2)下图中一共有( )个三角形,其中锐角三角形有( )个,直角三角形有( )个,钝角三角形有( )个。
180°
3
4
3
10
1.课前要让学生多准备各种三角形,通过动手操作使学生明白三角形内角和的含义。
2.通过图形的变形,使学生灵活运用三角形内角和去解决生活中的问题。
任务驱动
1.什么是三角形的内角 什么是三角形的内角和
三角形中相邻两边组成的角叫作三角形的内角。
三角形三个内角的和叫作三角形的内角和。
2.通过以下操作活动你发现了什么呢
三角形的三个内角拼在一起,正好构成一个平角。
3.你能画一个有两个内角是直角的三角形吗
4.直角三角形中两个锐角的和是多少度
不能,一个三角形最多只能有一个直角。
90°
5.一个三角形至少有几个锐角 为什么
两个锐角。如果只有一个锐角,那么就会有两个直角或钝角,这时三角形的内角和会超过180°。
6.等腰三角形和等边三角形的角有什么特点
等腰三角形的两个底角相等。
等边三角形的三个角都相等,都是60°。
归纳总结
1.三角形的内角和是180°。
2.等腰三角形的底角相等。等边三角形的三个角都相等,它们的度数都是60°。
1.填一填。
(1)在直角三角形中,一个锐角是54°,另一个锐角是( )。
(2)等边三角形每个内角都是( )。
(3)在一个三角形中,两个内角的度数分别为30°和75°,则另一个内角的度数为( )。这是一个( )三角形,也是一个( )三角形。
36°
锐角
等腰
75°
60°
2.根据条件算出角的度数。( 综合类作业)
(1)如图,已知∠4=143°,∠1=72°,求∠2和∠3的度数。
∠2=180°-143°=37°
∠3=180°-72°-37°=71°
(2)一个等腰三角形,它的一个底角是40°,它的顶角是多少度
180°-40°-40°=100°
3.下图是两块三角形木板破碎后留下的碎片,你知道它们原来的形状分别是什么三角形吗 ( 实践类作业)
先用量角器量出两块三角形木板碎片上剩余2个角的度数。
(1)180°-45°-60°=75°
答:第一块木板原来的形状是锐角三角形。
(2)180°-60°-30°=90°
答:第二块木板原来的形状是直角三角形。
END
感谢观看 下节课再会
