2023年高考数学客观题专题二 复数 课件(共34张PPT)
文档属性
| 名称 | 2023年高考数学客观题专题二 复数 课件(共34张PPT) | 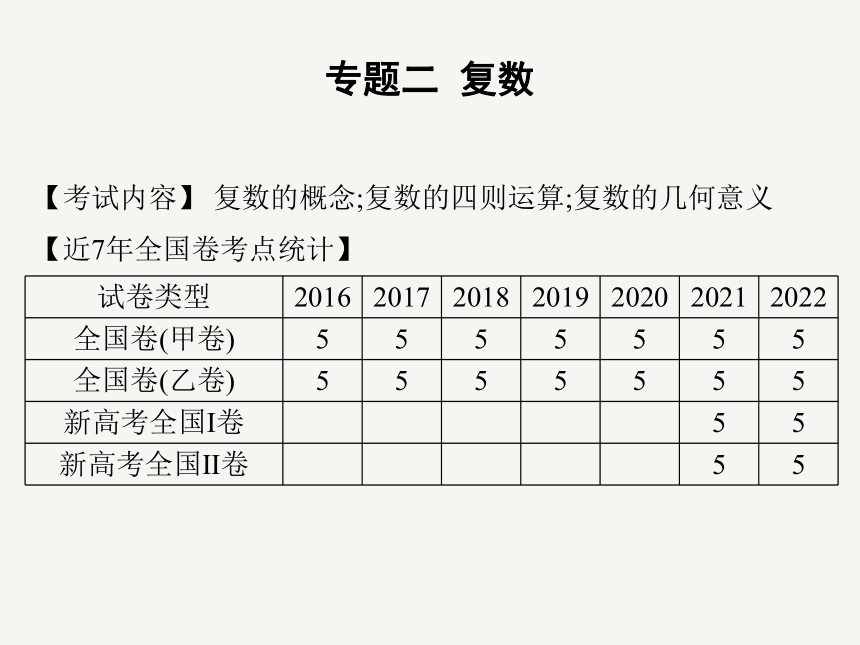 | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 12:25:10 | ||
图片预览












文档简介
(共34张PPT)
专题二 复数
【考试内容】 复数的概念;复数的四则运算;复数的几何意义
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 5 5 5 5 5 5 5
全国卷(乙卷) 5 5 5 5 5 5 5
新高考全国Ⅰ卷 5 5
新高考全国Ⅱ卷 5 5
重要考点回顾
一、复数的概念
1.定义:形如a+bi(a,b∈R)的数叫做复数,记作z=a+bi,其中i是虚数单位,i2=-1;a与b分别叫做复数z=a+bi的实部和虚部.
2.分类:设复数z=a+bi(a,b∈R)
(1)当b=0时,z为实数;
(2)当b≠0时,z为虚数;
(3)当a=0,且b≠0时,z为纯虚数.
3.复数相等:如果两个复数实部相等且虚部相等就说这两个复数相等.
4.共轭复数:当两个复数实部相等,虚部互为相反数时.这两个复数互为共轭复数,也即z=a+bi,则 =a-bi.
5.z=a+bi(a,b∈R)的模(或绝对值):
6.复平面:建立直角坐标系来表示复数的平面叫做复平面,x轴叫做实轴,y轴(不包含原点)叫虚轴.
则复数z=a+bi(a,b∈R)与复平面上的点(a,b)建立了一一对应的关系.
二、复数的运算
设复数z1=a+bi,z2=c+di(a,b,c,d∈R),则
1.(a+bi)+(c+di)=(a+c)+(b+d)i;
2.(a+bi)-(c+di)=(a-c)+(b-d)i;
3.(a+bi)(c+di)=(ac-bd)+(bc+ad)i;
4.(a+bi)÷(c+di)= (c+di≠0).
考点训练
1.若复数(1+bi)(2+i)是纯虚数(i是虚数单位,b是实数),则b=( )
A.-2 B.- C. D.2
【答案】 D
【解析】 ∵(1+bi)(2+i)=(2-b)+(1+2b)i为纯虚数,
∴2-b=0,∴b=2.故选D.
2.设(1+2i)(a+i)的实部和虚部相等,其中a为实数,则a= ( )
A.-3 B.-2 C.2 D.3
【答案】 A
【解析】 ∵(1+2i)(a+i)=(a-2)+(2a+1)i,
∴a-2=2a+1,∴a=-3.
故选A.
3.i是虚数单位,1+i3等于 ( )
A.i B.-i C.1+i D.1-i
【答案】 D
【解析】 i3=-i,1+i3=1-i.故选D.
4.i是虚数单位,若集合S={-1,0,1},则 ( )
A.i∈S B.i2∈S C.i3∈S D.∈S
【答案】 B
【解析】 i2=-1.故选B.
5.设a,b∈R,则“ab=0”是“复数a+为纯虚数”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】 B
【解析】 因为复数a+为纯虚数,推得a=0且b≠0,所以ab=0.
所以“ab=0”是“复数a+为纯虚数”的必要条件.而“ab=0”无法推得“a=0,b≠0”(可能a不为0,b为0或a,b同时为0),即无法推得“复数a+为纯虚数”,所以“ab=0”不是“复数a+为纯虚数”的充分条件.
综上,“ab=0”是“复数a+为纯虚数”的必要不充分条件.故选B.
6.设z的共轭复数是,若z+=4,z·=8,则等于 ( )
A.i B.-i C.±1 D.±i
【答案】 D
【解析】 设z=a+bi,则=a-bi,
由条件可得解得a=2,b=±2,
于是有====±i.故选D.
7.复数z=的共轭复数是 ( )
A.2+i B.2-i C.-1+i D.-1-i
【答案】 D
【解析】 因为复数z===-1+i,
所以有=-1-i.故选D.
8.设a,b∈R,a+bi=(i为虚数单位),则a+b的值为 .
【答案】 8
【解析】 因为复数a+bi====5+3i,
故a+b=8.
9.i是虚数单位,在复平面内复数对应的点所在的象限为( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【答案】 D
【解析】 ===2-i.
复数对应的点为(2,-1),即在第四象限.故选D.
10.已知0A.(1,5) B.(1,3) C.(1,) D.(1,)
【答案】 C
【解析】 因为|z|=,而0于是1<<.故选C.
11.若复数z满足z(2-i)=11+7i(i为虚数单位),则|z|为 ( )
A.4 B.-4 C. D.-
【答案】 C
【解析】 由z(2-i)=11+7i,得z===3+5i,
于是|z|==.故选C.
12.在复平面内,复数对应的点的坐标为 ( )
A.(1,3) B.(3,1) C.(-1,3) D.(3,-1)
【答案】 A
【解析】 由==1+3i,得在复平面上对应的点的坐标为(1,3).故选A.
13.设复数z满足iz=1,其中i为虚数单位,则z= ( )
A.-i B.i C.-1 D.1
【答案】 A
【解析】 由iz=1得z==-i.故选A.
14.若a为实数,且=3+i,则a= ( )
A.-4 B.-3 C.3 D.4
【答案】 D
【解析】 由题意可得2+ai=(1+i)(3+i)=2+4i a=4.故选D.
15.复数= ( )
A.i B.-i C.--i D.-+i
【答案】 A
【解析】 ===i.故选A.
16.已知复数z=1-i,则= ( )
A.2 B.-2 C.2i D.-2i
【答案】 A
【解析】 ===2.故选A.
17.i是虚数单位,i(1+i)等于 ( )
A.1+i B.-1-i C.1-i D.-1+i
【答案】 D
【解析】 i(1+i)=i+i2=-1+i.故选D.
18.设复数z=1+i(i是虚数单位),则+z2= ( )
A.1+i B.-1+i C.1-i D.-1-i
【答案】 A
【解析】 +z2=+(1+i)2=+(1+2i+i2)=(1-i)+2i=1+i.
故选A.
19.设复数z=(m2-8m+15)+(m2-5m+6)i(m∈R),则当z表示实数时,m的值为 ( )
A.3 B.5
C.3或5 D.2或3
【答案】 D
【解析】 由题意得m2-5m+6=0,解得m=2或m=3.故选D.
20.复数z=(a2-2a)+(a2-a-2)i(a∈R)在复平面内对应的点在虚轴上,则实数a满足 ( )
A.a≠2或a≠1 B.a≠2且a≠1
C.a=2或a=0 D.a=0
【答案】 D
【解析】 由题意得解得a=0.故选D.
21.(多选题)设复数z=-+i,则以下结论正确的是 ( )
A.z2≥0 B.z2= C.z3=1 D.z2020=z
【答案】 BCD
【解析】 ∵z=-+i,
∴z2==-i-=--i,故A错误;
z2=,故B正确;
z3=z2·z==-i+i+=1,故C正确;
z2020=z3×673·z=z,故D正确.故选BCD.
22.(多选题)已知复数z=+i(i为虚数单位),为z的共轭复数,若复数z0=,则下列结论正确的是 ( )
A.z0在复平面内对应的点位于第四象限
B.|z0|=1
C.z0的实部为
D.z0的虚部为
【答案】 ABC
【解析】 ∵z=+i,
∴z0======-i.
则z0在复平面内对应的点位于第四象限,故A正确;
|z0|=,故B正确;
|z0|的实部为,故C正确;
|z0|的虚部为-,故D错误.故选ABC.
23.(多选题)下列结论正确的是 ( )
A.若复数z满足z+=0,则z为纯虚数
B.若复数z满足∈R,则z∈R
C.若复数z满足z2≥0,则z∈R
D.若复数z1,z2满足+=0,则z1=z2=0
【答案】 BC
【解析】 若z=0,则z+=0,故A错误;
设z=a+bi(a,b∈R),则=-i∈R,
故=0,即b=0,故z∈R,故B正确;
因为z2=(a+bi)2=a2+2abi-b2≥0,则a2-b2≥0,且2ab=0,
所以b=0,故z∈R,故C正确;
若z1=1,z2=i,则满足+=0,故D错误.故选BC.
24.(多选题)已知复数z=cos 140°+isin 140°,i为虚数单位,则下列说法正确的是 ( )
A.z的虚部为isin 140°
B.z在复平面上对应的点位于第二象限
C.z=
D.z3=+i
【答案】 BCD
【解析】 ∵z=cos 140°+isin 140°,
∴z的虚部为sin 140°,故A错误;
z在复平面上对应的点的坐标为(cos 140°,sin 140°),
∵cos 140°<0,sin 140°>0,
∴点(cos 140°,sin 140°)位于第二象限,故B正确;
∵z·=|z|2=cos2140°+sin2140°=1,∴z=,故C正确;
z3=(cos 140°+isin 140°)3=cos 420°+isin 420°
=cos 60°+isin 60°=+i,故D正确.故选BCD.
25.(多选题)已知复数z=1+cos 2θ+isin 2θ(其中i为虚数单位),下列说法正确的是 ( )
A.复数z在复平面上对应的点可能落在第二象限
B.z可能为实数
C.|z|=2cos θ
D.的实部为
【答案】 BCD
【解析】 z=1+cos 2θ+isin 2θ=2cos θ(cos θ+isin θ),
∵-<θ<.
∴cos θ>0,sin θ∈(-1,1).
则复数z在复平面上对应的点不可能落在第二象限,故A错误;
当θ=0时,则z=2,即z可能为实数,故B正确;
|z|=2cos θ,故C正确;
∵===-i,∴的实部为,故D正确.故选BCD.
专题二 复数
【考试内容】 复数的概念;复数的四则运算;复数的几何意义
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 5 5 5 5 5 5 5
全国卷(乙卷) 5 5 5 5 5 5 5
新高考全国Ⅰ卷 5 5
新高考全国Ⅱ卷 5 5
重要考点回顾
一、复数的概念
1.定义:形如a+bi(a,b∈R)的数叫做复数,记作z=a+bi,其中i是虚数单位,i2=-1;a与b分别叫做复数z=a+bi的实部和虚部.
2.分类:设复数z=a+bi(a,b∈R)
(1)当b=0时,z为实数;
(2)当b≠0时,z为虚数;
(3)当a=0,且b≠0时,z为纯虚数.
3.复数相等:如果两个复数实部相等且虚部相等就说这两个复数相等.
4.共轭复数:当两个复数实部相等,虚部互为相反数时.这两个复数互为共轭复数,也即z=a+bi,则 =a-bi.
5.z=a+bi(a,b∈R)的模(或绝对值):
6.复平面:建立直角坐标系来表示复数的平面叫做复平面,x轴叫做实轴,y轴(不包含原点)叫虚轴.
则复数z=a+bi(a,b∈R)与复平面上的点(a,b)建立了一一对应的关系.
二、复数的运算
设复数z1=a+bi,z2=c+di(a,b,c,d∈R),则
1.(a+bi)+(c+di)=(a+c)+(b+d)i;
2.(a+bi)-(c+di)=(a-c)+(b-d)i;
3.(a+bi)(c+di)=(ac-bd)+(bc+ad)i;
4.(a+bi)÷(c+di)= (c+di≠0).
考点训练
1.若复数(1+bi)(2+i)是纯虚数(i是虚数单位,b是实数),则b=( )
A.-2 B.- C. D.2
【答案】 D
【解析】 ∵(1+bi)(2+i)=(2-b)+(1+2b)i为纯虚数,
∴2-b=0,∴b=2.故选D.
2.设(1+2i)(a+i)的实部和虚部相等,其中a为实数,则a= ( )
A.-3 B.-2 C.2 D.3
【答案】 A
【解析】 ∵(1+2i)(a+i)=(a-2)+(2a+1)i,
∴a-2=2a+1,∴a=-3.
故选A.
3.i是虚数单位,1+i3等于 ( )
A.i B.-i C.1+i D.1-i
【答案】 D
【解析】 i3=-i,1+i3=1-i.故选D.
4.i是虚数单位,若集合S={-1,0,1},则 ( )
A.i∈S B.i2∈S C.i3∈S D.∈S
【答案】 B
【解析】 i2=-1.故选B.
5.设a,b∈R,则“ab=0”是“复数a+为纯虚数”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】 B
【解析】 因为复数a+为纯虚数,推得a=0且b≠0,所以ab=0.
所以“ab=0”是“复数a+为纯虚数”的必要条件.而“ab=0”无法推得“a=0,b≠0”(可能a不为0,b为0或a,b同时为0),即无法推得“复数a+为纯虚数”,所以“ab=0”不是“复数a+为纯虚数”的充分条件.
综上,“ab=0”是“复数a+为纯虚数”的必要不充分条件.故选B.
6.设z的共轭复数是,若z+=4,z·=8,则等于 ( )
A.i B.-i C.±1 D.±i
【答案】 D
【解析】 设z=a+bi,则=a-bi,
由条件可得解得a=2,b=±2,
于是有====±i.故选D.
7.复数z=的共轭复数是 ( )
A.2+i B.2-i C.-1+i D.-1-i
【答案】 D
【解析】 因为复数z===-1+i,
所以有=-1-i.故选D.
8.设a,b∈R,a+bi=(i为虚数单位),则a+b的值为 .
【答案】 8
【解析】 因为复数a+bi====5+3i,
故a+b=8.
9.i是虚数单位,在复平面内复数对应的点所在的象限为( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【答案】 D
【解析】 ===2-i.
复数对应的点为(2,-1),即在第四象限.故选D.
10.已知0
【答案】 C
【解析】 因为|z|=,而0
11.若复数z满足z(2-i)=11+7i(i为虚数单位),则|z|为 ( )
A.4 B.-4 C. D.-
【答案】 C
【解析】 由z(2-i)=11+7i,得z===3+5i,
于是|z|==.故选C.
12.在复平面内,复数对应的点的坐标为 ( )
A.(1,3) B.(3,1) C.(-1,3) D.(3,-1)
【答案】 A
【解析】 由==1+3i,得在复平面上对应的点的坐标为(1,3).故选A.
13.设复数z满足iz=1,其中i为虚数单位,则z= ( )
A.-i B.i C.-1 D.1
【答案】 A
【解析】 由iz=1得z==-i.故选A.
14.若a为实数,且=3+i,则a= ( )
A.-4 B.-3 C.3 D.4
【答案】 D
【解析】 由题意可得2+ai=(1+i)(3+i)=2+4i a=4.故选D.
15.复数= ( )
A.i B.-i C.--i D.-+i
【答案】 A
【解析】 ===i.故选A.
16.已知复数z=1-i,则= ( )
A.2 B.-2 C.2i D.-2i
【答案】 A
【解析】 ===2.故选A.
17.i是虚数单位,i(1+i)等于 ( )
A.1+i B.-1-i C.1-i D.-1+i
【答案】 D
【解析】 i(1+i)=i+i2=-1+i.故选D.
18.设复数z=1+i(i是虚数单位),则+z2= ( )
A.1+i B.-1+i C.1-i D.-1-i
【答案】 A
【解析】 +z2=+(1+i)2=+(1+2i+i2)=(1-i)+2i=1+i.
故选A.
19.设复数z=(m2-8m+15)+(m2-5m+6)i(m∈R),则当z表示实数时,m的值为 ( )
A.3 B.5
C.3或5 D.2或3
【答案】 D
【解析】 由题意得m2-5m+6=0,解得m=2或m=3.故选D.
20.复数z=(a2-2a)+(a2-a-2)i(a∈R)在复平面内对应的点在虚轴上,则实数a满足 ( )
A.a≠2或a≠1 B.a≠2且a≠1
C.a=2或a=0 D.a=0
【答案】 D
【解析】 由题意得解得a=0.故选D.
21.(多选题)设复数z=-+i,则以下结论正确的是 ( )
A.z2≥0 B.z2= C.z3=1 D.z2020=z
【答案】 BCD
【解析】 ∵z=-+i,
∴z2==-i-=--i,故A错误;
z2=,故B正确;
z3=z2·z==-i+i+=1,故C正确;
z2020=z3×673·z=z,故D正确.故选BCD.
22.(多选题)已知复数z=+i(i为虚数单位),为z的共轭复数,若复数z0=,则下列结论正确的是 ( )
A.z0在复平面内对应的点位于第四象限
B.|z0|=1
C.z0的实部为
D.z0的虚部为
【答案】 ABC
【解析】 ∵z=+i,
∴z0======-i.
则z0在复平面内对应的点位于第四象限,故A正确;
|z0|=,故B正确;
|z0|的实部为,故C正确;
|z0|的虚部为-,故D错误.故选ABC.
23.(多选题)下列结论正确的是 ( )
A.若复数z满足z+=0,则z为纯虚数
B.若复数z满足∈R,则z∈R
C.若复数z满足z2≥0,则z∈R
D.若复数z1,z2满足+=0,则z1=z2=0
【答案】 BC
【解析】 若z=0,则z+=0,故A错误;
设z=a+bi(a,b∈R),则=-i∈R,
故=0,即b=0,故z∈R,故B正确;
因为z2=(a+bi)2=a2+2abi-b2≥0,则a2-b2≥0,且2ab=0,
所以b=0,故z∈R,故C正确;
若z1=1,z2=i,则满足+=0,故D错误.故选BC.
24.(多选题)已知复数z=cos 140°+isin 140°,i为虚数单位,则下列说法正确的是 ( )
A.z的虚部为isin 140°
B.z在复平面上对应的点位于第二象限
C.z=
D.z3=+i
【答案】 BCD
【解析】 ∵z=cos 140°+isin 140°,
∴z的虚部为sin 140°,故A错误;
z在复平面上对应的点的坐标为(cos 140°,sin 140°),
∵cos 140°<0,sin 140°>0,
∴点(cos 140°,sin 140°)位于第二象限,故B正确;
∵z·=|z|2=cos2140°+sin2140°=1,∴z=,故C正确;
z3=(cos 140°+isin 140°)3=cos 420°+isin 420°
=cos 60°+isin 60°=+i,故D正确.故选BCD.
25.(多选题)已知复数z=1+cos 2θ+isin 2θ(其中i为虚数单位),下列说法正确的是 ( )
A.复数z在复平面上对应的点可能落在第二象限
B.z可能为实数
C.|z|=2cos θ
D.的实部为
【答案】 BCD
【解析】 z=1+cos 2θ+isin 2θ=2cos θ(cos θ+isin θ),
∵-<θ<.
∴cos θ>0,sin θ∈(-1,1).
则复数z在复平面上对应的点不可能落在第二象限,故A错误;
当θ=0时,则z=2,即z可能为实数,故B正确;
|z|=2cos θ,故C正确;
∵===-i,∴的实部为,故D正确.故选BCD.
同课章节目录
