2023年高考数学客观题专题九 不等式 课件(共28张PPT)
文档属性
| 名称 | 2023年高考数学客观题专题九 不等式 课件(共28张PPT) | 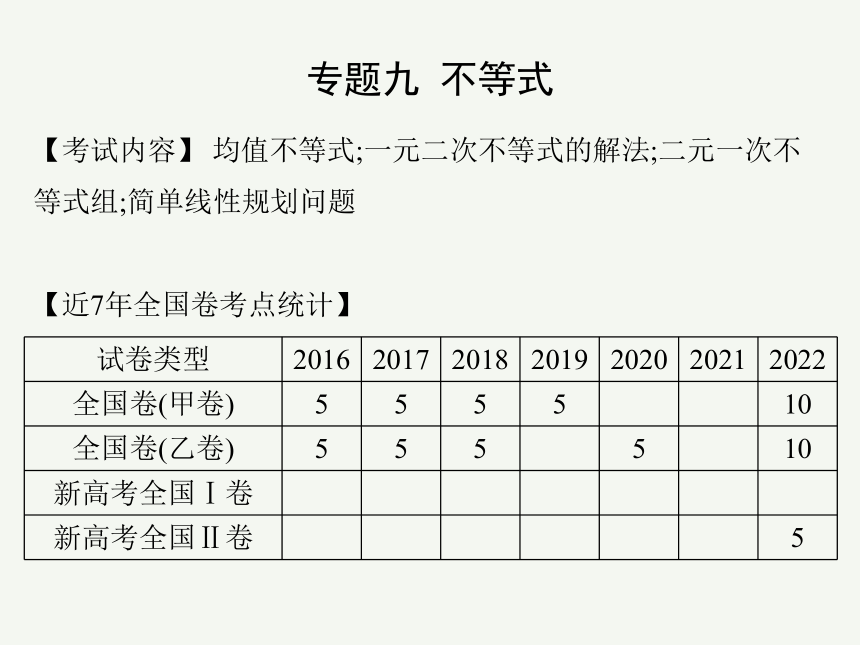 | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 12:25:32 | ||
图片预览








文档简介
(共28张PPT)
专题九 不等式
【考试内容】 均值不等式;一元二次不等式的解法;二元一次不等式组;简单线性规划问题
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 5 5 5 5 10
全国卷(乙卷) 5 5 5 5 10
新高考全国Ⅰ卷
新高考全国Ⅱ卷 5
重要考点回顾
一、均值不等式
两个数的算术平均数不小于它们的几何平均数.
若a,b>0,则 (当且仅当a=b时取等号)
基本变形:
基本应用:求函数最值:注意:①一正二定三取等;②积定和小,和定积大.
当ab=p(常数),当且仅当a=b时,a+b最小值为
当 a+b=S(常数),当且仅当a=b时,a·b最大值为
二、常用的基本不等式
1.设a,b∈R,则a2≥0,(a-b)2≥0(当且仅当a=b时取等号)
2.|a|≥a(当且仅当a≥0时取等号);|a|≥-a(当且仅当a≤0时取等号)
3.a>b,ab>0
注意:(1)特值法是判断不等式命题是否成立的一种方法,此法尤其适用于不成立的命题.
(2)另外需要特别注意:
①若ab>0,则 时,有a②如果对不等式两边同时乘以一个代数式,要注意它的正负号,如果正负号未定,要注意分类讨论.
③图象法:利用有关函数的图象(指数函数、对数函数、二次函数、三角函数的图象),直接比较大小.
④中介值法:先把要比较的代数式与“0”或“1”比,然后再比较它们的大小.
三、不等式的解法
1.一元一次不等式:
(1)ax>b(a≠0):①若a>0,则x> ;②若a<0,则x< ;
(2)ax0,则x< ;②若a<0,则x> ;
2.一元二次不等式:一元二次不等式二次项系数小于零的,同解变形为二次项系数大于零;
注:要对Δ进行讨论.
3.绝对值不等式:若a>0,则|x|a ;x<-a或x>a.
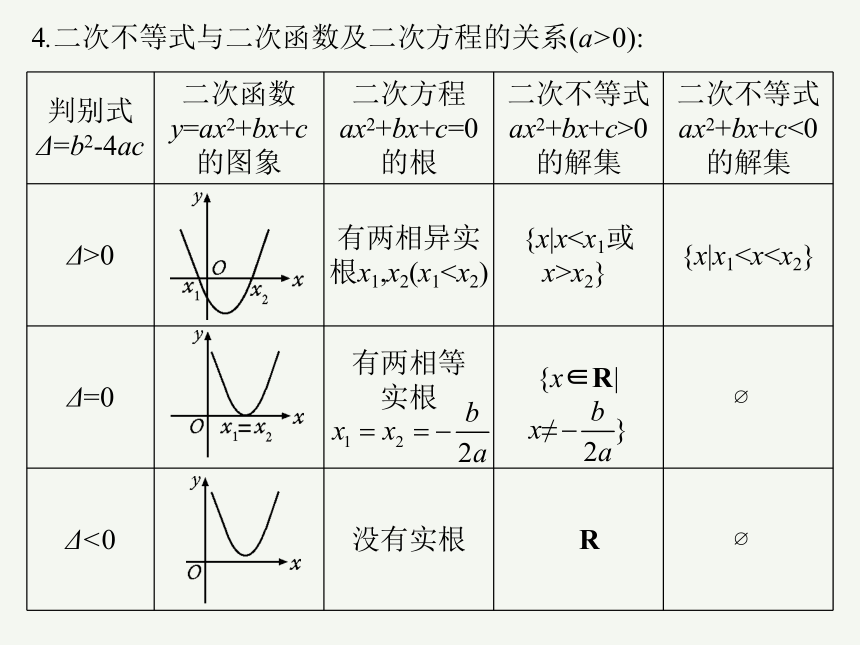
4.二次不等式与二次函数及二次方程的关系(a>0):
判别式 Δ=b2-4ac 二次函数 y=ax2+bx+c的图象 二次方程 ax2+bx+c=0的根 二次不等式 ax2+bx+c>0 的解集 二次不等式
ax2+bx+c<0
的解集
Δ>0 有两相异实根x1,x2(x1x2} {x|x1Δ=0 有两相等 实根 {x∈R| x≠ }
Δ<0 没有实根 R
考点训练
1.设a,b∈R,若a-|b|>0,则下列不等式中正确的是 ( )
A.b-a>0 B.a3+b3<0
C.b+a>0 D.a2-b2<0
【答案】C
【解析】特殊值法,取a=2,b=-1,
经验证,只有C成立.故选C.
2.设a>b>1,c<0,给出下列三个结论:
①>; ②acloga(b-c),
其中所有的正确结论的序号是 ( )
A.① B.①② C.②③ D.①②③
【答案】D
【解析】特殊值法,取a=3,b=2,c=-1,
经验证①②③均成立.故选D.
3.不等式<0的解集是 ( )
A.(1,+∞) B.(-∞,-2)
C.(-2,1) D.(-∞,-2)∪(1,+∞)
【答案】C
【解析】原不等式等价于(x-1)(x+2)<0,解得-24.不等式x2-5x+6≤0的解集为 .
【答案】[2,3]
【解析】原不等式等价于(x-2)(x-3)≤0,解得2≤x≤3,
故解集为[2,3].
5.不等式|x-1|<1的解集是 .
【答案】(0,2)
【解析】由-1故解集为(0,2).
6.设函数f(x)=则不等式f(x)>f(1)的解集是( )
A.(-3,1)∪(3,+∞) B.(-3,1)∪(2,+∞)
C.(-1,1)∪(3,+∞) D.(-∞,-3)∪(1,3)
【答案】A
【解析】因为f(1)=1-4+6=3,
所以不等式f(x)>f(1)的解集就是f(x)>3的解集.
于是有或
解得0≤x<1或x>3或-3即不等式f(x)>f(1)的解集是(-3,1)∪(3,+∞),故选A.
7.定义在R上的运算☉:a☉b=ab+2a+b,则满足x☉(x-2)<0的实数x的取值范围为 ( )
A.(0,2) B.(-2,1)
C.(-∞,-2)∪(1,+∞) D.(-1,2)
【答案】B
【解析】由题意可得x☉(x-2)=x(x-2)+2x+(x-2)=x2+x-2,
由x2+x-2<0得-2※8.设x,y,z∈R*,若x-2y+3z=0,则的最小值为 .
【答案】3
【解析】由x-2y+3z=0得y=(x+3z),
于是有==·=·,
因为x,z∈R*,由均值定理得+≥2=6,
所以有≥×(6+6)=3,当且仅当=时取等号.即的最小值为3.
※9.设x,y∈R,a>1,b>1,若ax=by=3,a+b=2,则+的最大值是( )
A.2 B. C.1 D.
【答案】C
【解析】由a>1,b>1,且ax=by=3得x=loga3,y=logb3,
于是有=log3a,=log3b,
从而有+=log3a+log3b=log3ab≤log3=log33=1.
当且仅当a=b时,上式等号成立,此时+取最大值1.故选C.
10.若正数x,y满足x+3y=5xy,则3x+4y的最小值是 ( )
A. B. C.5 D.6
【答案】C
【解析】由x+3y=5xy得+=5,
于是有3x+4y=(3x+4y)=≥=5.
故选C.
11.下列不等式恒成立的是 ( )
A.a2+b2≤2ab B.a2+b2≥-2ab
C.a+b≥2 D.a2+b2≤-2ab
【答案】B
【解析】显然当a<0,b>0时,不等式a2+b2≤2ab不成立,故A错误;
∵(a+b)2≥0,∴a2+b2+2ab≥0,∴a2+b2≥-2ab,故B正确;
显然当a<0,b<0时,不等式a+b≥2不成立,故C错误;
显然当a>0,b>0时,不等式a2+b2≤-2ab不成立,故D错误.
故选B.
12.若实数a,b满足a>b>0,则下列不等式中恒成立的是 ( )
A.a+b>2 B.a+b<2
C.+2b>2 D.+2b<2
【答案】A
【解析】因为a>b>0,所以a+b≥2,当且仅当a=b时取等号.
又a>b>0,所以a+b>2,故A正确,B错误;
+2b≥2=2,当且仅当=2b,即a=4b时取等号,故CD错误.
故选A.
13.下列函数中最小值为4的是 ( )
A.y=x2+2x+4 B.y=|sin x|+
C.y=2x+22-x D.y=ln x+
【答案】C
【解析】对于A,因为y=x2+2x+4=(x+1)2+3≥3,
所以函数的最小值为3.故A错误;
对于B,因为0<|sin x|≤1,所以y=|sin x|+≥2=4,
当且仅当|sin x|=,即|sin x|=2时取等号.
因为|sin x|≤1,所以等号取不到,所以y=|sin x|+>4.故B错误;
【解析】对于C,因为2x>0,所以y=2x+22-x=2x+≥2=4,
当且仅当2x=2,即x=1时取等号.
所以函数的最小值为4.故C正确;
对于D,因为当x=时,y=ln+=-1-4=-5<4,
所以函数的最小值不是4.故D错误.
故选C.
14.已知两两不相等的x1,y1,x2,y2,x3,y3,同时满足①x1A.2x2x1+x3
C.x1x3
【答案】A
【解析】设x1+y1=x2+y2=x3+y3=2m,
则有
根据题意,应该有且m2-a2+m2-c2=2(m2-b2)>0,
则有则x1+x3-2x2=(m-a)+(m-c)-2(m-b)=2b-(a+c).
因为(2b)2-(a+c)2=2(a2+c2)-(a+c)2>0,所以x1+x3-2x2=2b-(a+c)>0.
故A正确,B错误;
x1x3-=(m-a)(m-c)-(m-b)2=(2b-a-c)m+ac-b2=(2b-a-c)m-,
而上面已证2b-a-c>0,
因为不知道m的正负,所以该式子的正负无法恒定.
故选A.
15.(多选题)已知a>0,b>0,且a+b=1,则 ( )
A.a2+b2≥ B.2a-b>
C.log2a+log2b≥-2 D.+≤
【答案】ABD
【解析】对于A,已知a>0,b>0,且a+b=1,所以(a+b)2≤2a2+2b2,
则a2+b2≥,故A正确;
对于B,利用分析法:要证2a-b>,只需证明a-b>-1即可,即a>b-1,
由于a>0,b>0,且a+b=1,所以a>0,-1【解析】对于C,log2a+log2b=log2ab≤log2=-2,故C错误;
对于D,由于a>0,b>0,且a+b=1.
利用分析法:要证+≤成立,
只需对关系式进行平方,整理得a+b+2≤2,即2≤1,
故≤=,当且仅当a=b=时,等号成立.故D正确.
故选ABD.
16.已知函数f(x)=3x+(a>0)的最小值为5,则a= .
【答案】9
【解析】因为3x+1>0,且f(x)=3x+=3x+1+-1≥2-1=5,
所以a=9,经检验,3x=2时等号成立.
故答案为9.
17.已知a>0,b>0,且ab=1,则++的最小值为 .
【答案】4
【解析】a>0,b>0,且ab=1,
则++=+=+≥2=4,
当且仅当=,
即a=2+,b=2-或a=2-,b=2+时取等号.
故答案为4.
18.已知5x2y2+y4=1(x,y∈R),则x2+y2的最小值是 .
【答案】
【解析】由5x2y2+y4=1,可得x2=.
由x2≥0,可得y2∈(0,1].
则x2+y2=+y2==≥×2=,
当且仅当y2=,x2=时取等号.
可得x2+y2的最小值为.
专题九 不等式
【考试内容】 均值不等式;一元二次不等式的解法;二元一次不等式组;简单线性规划问题
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 5 5 5 5 10
全国卷(乙卷) 5 5 5 5 10
新高考全国Ⅰ卷
新高考全国Ⅱ卷 5
重要考点回顾
一、均值不等式
两个数的算术平均数不小于它们的几何平均数.
若a,b>0,则 (当且仅当a=b时取等号)
基本变形:
基本应用:求函数最值:注意:①一正二定三取等;②积定和小,和定积大.
当ab=p(常数),当且仅当a=b时,a+b最小值为
当 a+b=S(常数),当且仅当a=b时,a·b最大值为
二、常用的基本不等式
1.设a,b∈R,则a2≥0,(a-b)2≥0(当且仅当a=b时取等号)
2.|a|≥a(当且仅当a≥0时取等号);|a|≥-a(当且仅当a≤0时取等号)
3.a>b,ab>0
注意:(1)特值法是判断不等式命题是否成立的一种方法,此法尤其适用于不成立的命题.
(2)另外需要特别注意:
①若ab>0,则 时,有a
③图象法:利用有关函数的图象(指数函数、对数函数、二次函数、三角函数的图象),直接比较大小.
④中介值法:先把要比较的代数式与“0”或“1”比,然后再比较它们的大小.
三、不等式的解法
1.一元一次不等式:
(1)ax>b(a≠0):①若a>0,则x> ;②若a<0,则x< ;
(2)ax
2.一元二次不等式:一元二次不等式二次项系数小于零的,同解变形为二次项系数大于零;
注:要对Δ进行讨论.
3.绝对值不等式:若a>0,则|x|a ;x<-a或x>a.
4.二次不等式与二次函数及二次方程的关系(a>0):
判别式 Δ=b2-4ac 二次函数 y=ax2+bx+c的图象 二次方程 ax2+bx+c=0的根 二次不等式 ax2+bx+c>0 的解集 二次不等式
ax2+bx+c<0
的解集
Δ>0 有两相异实根x1,x2(x1
Δ<0 没有实根 R
考点训练
1.设a,b∈R,若a-|b|>0,则下列不等式中正确的是 ( )
A.b-a>0 B.a3+b3<0
C.b+a>0 D.a2-b2<0
【答案】C
【解析】特殊值法,取a=2,b=-1,
经验证,只有C成立.故选C.
2.设a>b>1,c<0,给出下列三个结论:
①>; ②ac
其中所有的正确结论的序号是 ( )
A.① B.①② C.②③ D.①②③
【答案】D
【解析】特殊值法,取a=3,b=2,c=-1,
经验证①②③均成立.故选D.
3.不等式<0的解集是 ( )
A.(1,+∞) B.(-∞,-2)
C.(-2,1) D.(-∞,-2)∪(1,+∞)
【答案】C
【解析】原不等式等价于(x-1)(x+2)<0,解得-2
【答案】[2,3]
【解析】原不等式等价于(x-2)(x-3)≤0,解得2≤x≤3,
故解集为[2,3].
5.不等式|x-1|<1的解集是 .
【答案】(0,2)
【解析】由-1
6.设函数f(x)=则不等式f(x)>f(1)的解集是( )
A.(-3,1)∪(3,+∞) B.(-3,1)∪(2,+∞)
C.(-1,1)∪(3,+∞) D.(-∞,-3)∪(1,3)
【答案】A
【解析】因为f(1)=1-4+6=3,
所以不等式f(x)>f(1)的解集就是f(x)>3的解集.
于是有或
解得0≤x<1或x>3或-3
7.定义在R上的运算☉:a☉b=ab+2a+b,则满足x☉(x-2)<0的实数x的取值范围为 ( )
A.(0,2) B.(-2,1)
C.(-∞,-2)∪(1,+∞) D.(-1,2)
【答案】B
【解析】由题意可得x☉(x-2)=x(x-2)+2x+(x-2)=x2+x-2,
由x2+x-2<0得-2
【答案】3
【解析】由x-2y+3z=0得y=(x+3z),
于是有==·=·,
因为x,z∈R*,由均值定理得+≥2=6,
所以有≥×(6+6)=3,当且仅当=时取等号.即的最小值为3.
※9.设x,y∈R,a>1,b>1,若ax=by=3,a+b=2,则+的最大值是( )
A.2 B. C.1 D.
【答案】C
【解析】由a>1,b>1,且ax=by=3得x=loga3,y=logb3,
于是有=log3a,=log3b,
从而有+=log3a+log3b=log3ab≤log3=log33=1.
当且仅当a=b时,上式等号成立,此时+取最大值1.故选C.
10.若正数x,y满足x+3y=5xy,则3x+4y的最小值是 ( )
A. B. C.5 D.6
【答案】C
【解析】由x+3y=5xy得+=5,
于是有3x+4y=(3x+4y)=≥=5.
故选C.
11.下列不等式恒成立的是 ( )
A.a2+b2≤2ab B.a2+b2≥-2ab
C.a+b≥2 D.a2+b2≤-2ab
【答案】B
【解析】显然当a<0,b>0时,不等式a2+b2≤2ab不成立,故A错误;
∵(a+b)2≥0,∴a2+b2+2ab≥0,∴a2+b2≥-2ab,故B正确;
显然当a<0,b<0时,不等式a+b≥2不成立,故C错误;
显然当a>0,b>0时,不等式a2+b2≤-2ab不成立,故D错误.
故选B.
12.若实数a,b满足a>b>0,则下列不等式中恒成立的是 ( )
A.a+b>2 B.a+b<2
C.+2b>2 D.+2b<2
【答案】A
【解析】因为a>b>0,所以a+b≥2,当且仅当a=b时取等号.
又a>b>0,所以a+b>2,故A正确,B错误;
+2b≥2=2,当且仅当=2b,即a=4b时取等号,故CD错误.
故选A.
13.下列函数中最小值为4的是 ( )
A.y=x2+2x+4 B.y=|sin x|+
C.y=2x+22-x D.y=ln x+
【答案】C
【解析】对于A,因为y=x2+2x+4=(x+1)2+3≥3,
所以函数的最小值为3.故A错误;
对于B,因为0<|sin x|≤1,所以y=|sin x|+≥2=4,
当且仅当|sin x|=,即|sin x|=2时取等号.
因为|sin x|≤1,所以等号取不到,所以y=|sin x|+>4.故B错误;
【解析】对于C,因为2x>0,所以y=2x+22-x=2x+≥2=4,
当且仅当2x=2,即x=1时取等号.
所以函数的最小值为4.故C正确;
对于D,因为当x=时,y=ln+=-1-4=-5<4,
所以函数的最小值不是4.故D错误.
故选C.
14.已知两两不相等的x1,y1,x2,y2,x3,y3,同时满足①x1
C.
【答案】A
【解析】设x1+y1=x2+y2=x3+y3=2m,
则有
根据题意,应该有且m2-a2+m2-c2=2(m2-b2)>0,
则有则x1+x3-2x2=(m-a)+(m-c)-2(m-b)=2b-(a+c).
因为(2b)2-(a+c)2=2(a2+c2)-(a+c)2>0,所以x1+x3-2x2=2b-(a+c)>0.
故A正确,B错误;
x1x3-=(m-a)(m-c)-(m-b)2=(2b-a-c)m+ac-b2=(2b-a-c)m-,
而上面已证2b-a-c>0,
因为不知道m的正负,所以该式子的正负无法恒定.
故选A.
15.(多选题)已知a>0,b>0,且a+b=1,则 ( )
A.a2+b2≥ B.2a-b>
C.log2a+log2b≥-2 D.+≤
【答案】ABD
【解析】对于A,已知a>0,b>0,且a+b=1,所以(a+b)2≤2a2+2b2,
则a2+b2≥,故A正确;
对于B,利用分析法:要证2a-b>,只需证明a-b>-1即可,即a>b-1,
由于a>0,b>0,且a+b=1,所以a>0,-1
对于D,由于a>0,b>0,且a+b=1.
利用分析法:要证+≤成立,
只需对关系式进行平方,整理得a+b+2≤2,即2≤1,
故≤=,当且仅当a=b=时,等号成立.故D正确.
故选ABD.
16.已知函数f(x)=3x+(a>0)的最小值为5,则a= .
【答案】9
【解析】因为3x+1>0,且f(x)=3x+=3x+1+-1≥2-1=5,
所以a=9,经检验,3x=2时等号成立.
故答案为9.
17.已知a>0,b>0,且ab=1,则++的最小值为 .
【答案】4
【解析】a>0,b>0,且ab=1,
则++=+=+≥2=4,
当且仅当=,
即a=2+,b=2-或a=2-,b=2+时取等号.
故答案为4.
18.已知5x2y2+y4=1(x,y∈R),则x2+y2的最小值是 .
【答案】
【解析】由5x2y2+y4=1,可得x2=.
由x2≥0,可得y2∈(0,1].
则x2+y2=+y2==≥×2=,
当且仅当y2=,x2=时取等号.
可得x2+y2的最小值为.
同课章节目录
