2023年高考数学客观题专题十二 计数原理 课件(共31张PPT)
文档属性
| 名称 | 2023年高考数学客观题专题十二 计数原理 课件(共31张PPT) | 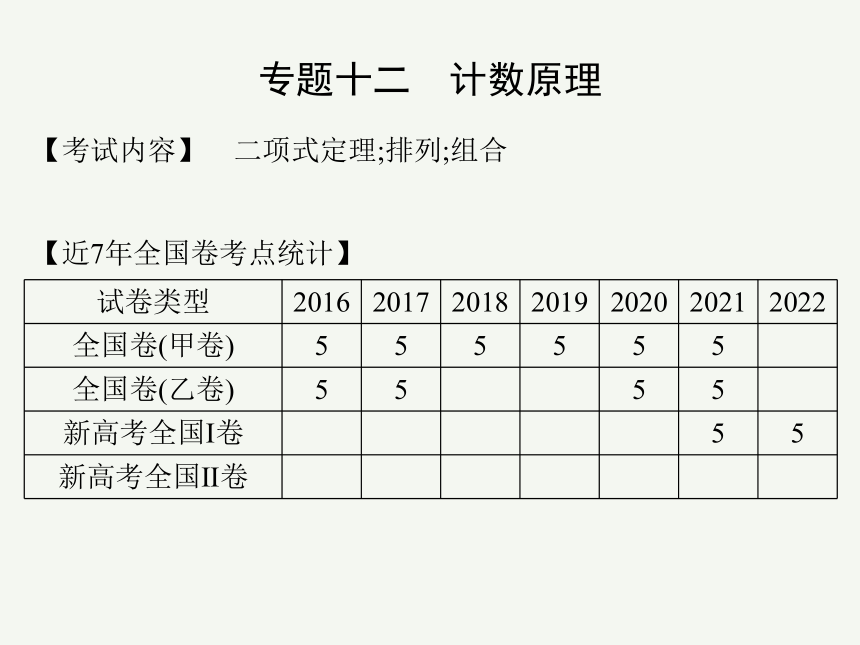 | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 12:26:14 | ||
图片预览












文档简介
(共31张PPT)
专题十二 计数原理
【考试内容】 二项式定理;排列;组合
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 5 5 5 5 5 5
全国卷(乙卷) 5 5 5 5
新高考全国Ⅰ卷 5 5
新高考全国Ⅱ卷
重要考点回顾
一、计数原理
1.分类计数原理(加法原理):N=m1+m2+…+mn.
2.分步计数原理(乘法原理):N=m1·m2·…·mn.
二、排列与组合
(一)排列
1.排列:一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
(二)组合
1.组合:一般地,从n个不同元素中取出m(m≤n)个元素合成一组,叫做从n个不同元素中取出m个元素的一个组合.
2.组合数公式
3.组合数的两个性质
考点训练
1.的展开式中x4的系数为 ( )
A.10 B.20 C.40 D.80
【答案】C
【解析】Tr+1=(x2)5-r=2rx10-3r,由10-3r=4,得r=2,
所以x4的系数为×22=40.故选C.
2.设i为虚数单位,则(x+i)6的展开式中含x4的项为 ( )
A.-15x4 B.15x4 C.-20ix4 D.20ix4
【答案】A
【解析】通项Tr+1=x6-rir(r=0,1,2,…,6),
令r=2,得含x4的项为x4i2=-15x4.
故选A.
3.(1+x)6的展开式中x2的系数为 ( )
A.15 B.20 C.30 D.35
【答案】C
【解析】(1+x)6展开式中含x2的项为1·x2+·x4=30x2,故x2的系数为30.故选C.
4.(x+y)(2x-y)5的展开式中x3y3的系数为 ( )
A.-80 B.-40 C.40 D.80
【答案】C
【解析】(2x-y)5的展开式的通项公式为Tr+1=(2x)5-r(-y)r.
当r=3时,x(2x-y)5展开式中x3y3的系数为×22×(-1)3=-40,
当r=2时,y(2x-y)5展开式中x3y3的系数为×23×(-1)2=80,
所以x3y3的系数为80-40=40.故选C.
5.二项式(x+1)n(n∈N+)的展开式中x2的系数为15,则n= ( )
A.4 B.5 C.6 D.7
【答案】C
【解析】由(x+1)n=(1+x)n=1+x+x2+…+xn,可知=15.
由=15,解得n=6或n=-5(舍去).故选C.
6.在(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),则f(3,0)+f(2,1)+f(1,2)+f(0,3)= ( )
A.45 B.60 C.120 D. 210
【答案】C
【解析】由题意知f(3,0)=,f(2,1)=,f(1,2)=,f(0,3)=,
因此f(3,0)+f(2,1)+f(1,2)+f(0,3)=120.故选C.
7.已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为 ( )
A.212 B.211 C.210 D.29
【答案】D
【解析】因为(1+x)n的展开式中的第4项与第8项的二项式系数相等,所以由=,解得n=10.
所以二项式(1+x)10的展开式中奇数项的二项式系数和为×210=29.故选D.
8.若(a+x)(1+x)4的展开式中x的奇数次幂项的系数之和为32,则a= .
【答案】3
【解析】(1+x)4展开式的通项为Tr+1=xr,
由题意可知a(+)+++=32,解得a=3.
9.若的展开式中x3项的系数为20,则a2+b2的最小值
为 .
【答案】2
【解析】Tr+1=(ax2)6-r=a6-rbrx12-3r,
令12-3r=3,得r=3,故a3b3=20,
∴ab=1,a2+b2≥2ab=2,当且仅当a=b=1或a=b=-1时等号成立.
10.若将函数f(x)=x5表示为f(x)=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,其中a0,a1,a2,…,a5为实数,则a3= .
【答案】10
【解析】 方法一:由等式两边对应项系数相等.
即 a3=10.
方法二:对等式:f(x)=x5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5
两边连续对x求导三次得60x2=6a3+24a4(1+x)+60a5(1+x)2,
再运用赋值法,令x=-1得60=6a3,即a3=10.
方法三:f(x)=x5=(-1+1+x)5,则a3=(-1)2=10.
11.安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )
A.12种 B.18种 C.24种 D.36种
【答案】D
【解析】由题意可得,一人完成两项工作,其余两人每人完成一项工作.
据此可得,只要把工作分成三份,有种方法,
然后进行全排列.
由乘法原理,不同的安排方式共有·=36(种).故选D.
12.用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为 ( )
A.24 B.48 C.60 D.72
【答案】D
【解析】由题意,要组成没有重复的五位奇数,则个位数应该为1,3,5中任选一个,有种方法,
其他数位上的数可以从剩下的4个数字中任选,进行全排列,有种方法,
所以其中奇数的个数为=72.故选D.
13.用0,1,…,9十个数字,可以组成有重复数字的三位数的个数
为 ( )
A.243 B.252 C.261 D.279
【答案】B
【解析】能够组成三位数的个数是9×10×10=900,
能够组成无重复数字的三位数的个数是9×9×8=648.
故能够组成有重复数字的三位数的个数为900-648=252.
故选B.
14.用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有 ( )
A.144个 B.120个 C.96个 D.72个
【答案】B
【解析】据题意,万位上只能排4,5.
若万位上排4,则有2×(个);
若万位上排5,则有3×(个).
所以共有2×+3×=5×24=120(个).故选B.
15.4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为 ( )
A. B. C. D.
【答案】 D
【解析】P==.故选D.
16.将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有 ( )
A.12种 B.10种 C.9种 D.8种
【答案】 A
【解析】先安排1名教师和2名学生到甲地,
再将剩下的1名教师和2名学生安排到乙地,
共有=12(种).故选A.
17.若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有 ( )
A.60种 B.63种 C.65种 D.66种
【答案】 D
【解析】和为偶数,则4个数都是偶数,都是奇数或者两个奇数两个偶数,
则有++·=1+5+60=66(种)取法.故选D.
18.现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这3张卡片不能是同一种颜色,并且红色卡片至多1张,则不同取法的种数是 ( )
A.232 B.252 C.472 D.484
【答案】 C
【解析】若没有红色卡片,则需从黄、蓝、绿三色卡片中选3张,若都不同色则有··=64(种);
若2张同色,则有···=144(种);
若红色1张,其余2张不同色,则有···=192(种);其余2张同色则有··=72(种).所以共有64+144+192+72=472(种).故选C.
19.某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位,节目乙不能排在第一位,节目丙必须排在最后一位,则该台晚会节目演出顺序的编排方案共有 ( )
A.36种 B.42种 C.48种 D.54种
【答案】 B
【解析】分两类:一类为甲排在第一位共有=24(种),
另一类甲排在第二位共有=18(种),
故编排方案共有24+18=42(种).故选B.
20.现安排甲、乙、丙、丁、戊5名同学参加上海世博会志愿者服务活动,每人从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加。甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是( )
A.152 B.126 C.90 D.54
【答案】 B
【解析】由于五个人从事四项工作,而每项工作至少一人,那么每项工作至多两人,因为甲、乙不会开车,所以只能先安排司机,分两类:
(1)先从丙、丁、戊三人中任选一人开车;再从其余四人中任选两人作为一个元素同其他两人从事其他三项工作,共有(种);
(2)先从丙、丁、戊三人中任选两人开车:其余三人从事其他三项工作,共有(种).
所以不同安排方案的种数是+=126(种).故选B.
21.从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有 种不同的选法(用数字作答).
【答案】 660
【解析】分两步:
第一步,选出4人,由于至少1名女生,故有-=55(种)不同的选法;
第二步,从4人中选出队长、副队长各一人,有=12(种)不同的选法,
根据分步乘法计数原理共有55×12=660(种)不同的选法.
22.10件产品中有7件正品,3件次品,从中任取4件,则恰好取到1件次品的概率是 .
【答案】
【解析】从10件产品中任取4件共有=210(种)不同取法.
因为10件产品中有7件正品,3件次品,
所以从中任取4件恰好取到1件次品共有=105(种)不同的取法,
故所求的概率为P==.
23.将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少一张,如果分给同一人的两张参观券连号,那么不同的分法种数是 .
【答案】 96
【解析】5张参观券分成4堆,有2个联号有4种分法,每种分法分给4个人有种方法,所以总共有4=96(种).
24.将A,B,C,D,E,F六个字母排成一排,且A,B均在C的同侧,则不同的排法共有 种(用数字作答).
【答案】 480
【解析】第一类,字母C排在左边第一个位置,有(种);
第二类,字母C排在左边第二个位置,有(种);
第三类,字母C排在左边第三个位置,有+(种),
由对称性可知共有2×(+++)=480(种).
专题十二 计数原理
【考试内容】 二项式定理;排列;组合
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 5 5 5 5 5 5
全国卷(乙卷) 5 5 5 5
新高考全国Ⅰ卷 5 5
新高考全国Ⅱ卷
重要考点回顾
一、计数原理
1.分类计数原理(加法原理):N=m1+m2+…+mn.
2.分步计数原理(乘法原理):N=m1·m2·…·mn.
二、排列与组合
(一)排列
1.排列:一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
(二)组合
1.组合:一般地,从n个不同元素中取出m(m≤n)个元素合成一组,叫做从n个不同元素中取出m个元素的一个组合.
2.组合数公式
3.组合数的两个性质
考点训练
1.的展开式中x4的系数为 ( )
A.10 B.20 C.40 D.80
【答案】C
【解析】Tr+1=(x2)5-r=2rx10-3r,由10-3r=4,得r=2,
所以x4的系数为×22=40.故选C.
2.设i为虚数单位,则(x+i)6的展开式中含x4的项为 ( )
A.-15x4 B.15x4 C.-20ix4 D.20ix4
【答案】A
【解析】通项Tr+1=x6-rir(r=0,1,2,…,6),
令r=2,得含x4的项为x4i2=-15x4.
故选A.
3.(1+x)6的展开式中x2的系数为 ( )
A.15 B.20 C.30 D.35
【答案】C
【解析】(1+x)6展开式中含x2的项为1·x2+·x4=30x2,故x2的系数为30.故选C.
4.(x+y)(2x-y)5的展开式中x3y3的系数为 ( )
A.-80 B.-40 C.40 D.80
【答案】C
【解析】(2x-y)5的展开式的通项公式为Tr+1=(2x)5-r(-y)r.
当r=3时,x(2x-y)5展开式中x3y3的系数为×22×(-1)3=-40,
当r=2时,y(2x-y)5展开式中x3y3的系数为×23×(-1)2=80,
所以x3y3的系数为80-40=40.故选C.
5.二项式(x+1)n(n∈N+)的展开式中x2的系数为15,则n= ( )
A.4 B.5 C.6 D.7
【答案】C
【解析】由(x+1)n=(1+x)n=1+x+x2+…+xn,可知=15.
由=15,解得n=6或n=-5(舍去).故选C.
6.在(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),则f(3,0)+f(2,1)+f(1,2)+f(0,3)= ( )
A.45 B.60 C.120 D. 210
【答案】C
【解析】由题意知f(3,0)=,f(2,1)=,f(1,2)=,f(0,3)=,
因此f(3,0)+f(2,1)+f(1,2)+f(0,3)=120.故选C.
7.已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为 ( )
A.212 B.211 C.210 D.29
【答案】D
【解析】因为(1+x)n的展开式中的第4项与第8项的二项式系数相等,所以由=,解得n=10.
所以二项式(1+x)10的展开式中奇数项的二项式系数和为×210=29.故选D.
8.若(a+x)(1+x)4的展开式中x的奇数次幂项的系数之和为32,则a= .
【答案】3
【解析】(1+x)4展开式的通项为Tr+1=xr,
由题意可知a(+)+++=32,解得a=3.
9.若的展开式中x3项的系数为20,则a2+b2的最小值
为 .
【答案】2
【解析】Tr+1=(ax2)6-r=a6-rbrx12-3r,
令12-3r=3,得r=3,故a3b3=20,
∴ab=1,a2+b2≥2ab=2,当且仅当a=b=1或a=b=-1时等号成立.
10.若将函数f(x)=x5表示为f(x)=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,其中a0,a1,a2,…,a5为实数,则a3= .
【答案】10
【解析】 方法一:由等式两边对应项系数相等.
即 a3=10.
方法二:对等式:f(x)=x5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5
两边连续对x求导三次得60x2=6a3+24a4(1+x)+60a5(1+x)2,
再运用赋值法,令x=-1得60=6a3,即a3=10.
方法三:f(x)=x5=(-1+1+x)5,则a3=(-1)2=10.
11.安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )
A.12种 B.18种 C.24种 D.36种
【答案】D
【解析】由题意可得,一人完成两项工作,其余两人每人完成一项工作.
据此可得,只要把工作分成三份,有种方法,
然后进行全排列.
由乘法原理,不同的安排方式共有·=36(种).故选D.
12.用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为 ( )
A.24 B.48 C.60 D.72
【答案】D
【解析】由题意,要组成没有重复的五位奇数,则个位数应该为1,3,5中任选一个,有种方法,
其他数位上的数可以从剩下的4个数字中任选,进行全排列,有种方法,
所以其中奇数的个数为=72.故选D.
13.用0,1,…,9十个数字,可以组成有重复数字的三位数的个数
为 ( )
A.243 B.252 C.261 D.279
【答案】B
【解析】能够组成三位数的个数是9×10×10=900,
能够组成无重复数字的三位数的个数是9×9×8=648.
故能够组成有重复数字的三位数的个数为900-648=252.
故选B.
14.用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有 ( )
A.144个 B.120个 C.96个 D.72个
【答案】B
【解析】据题意,万位上只能排4,5.
若万位上排4,则有2×(个);
若万位上排5,则有3×(个).
所以共有2×+3×=5×24=120(个).故选B.
15.4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为 ( )
A. B. C. D.
【答案】 D
【解析】P==.故选D.
16.将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有 ( )
A.12种 B.10种 C.9种 D.8种
【答案】 A
【解析】先安排1名教师和2名学生到甲地,
再将剩下的1名教师和2名学生安排到乙地,
共有=12(种).故选A.
17.若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有 ( )
A.60种 B.63种 C.65种 D.66种
【答案】 D
【解析】和为偶数,则4个数都是偶数,都是奇数或者两个奇数两个偶数,
则有++·=1+5+60=66(种)取法.故选D.
18.现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这3张卡片不能是同一种颜色,并且红色卡片至多1张,则不同取法的种数是 ( )
A.232 B.252 C.472 D.484
【答案】 C
【解析】若没有红色卡片,则需从黄、蓝、绿三色卡片中选3张,若都不同色则有··=64(种);
若2张同色,则有···=144(种);
若红色1张,其余2张不同色,则有···=192(种);其余2张同色则有··=72(种).所以共有64+144+192+72=472(种).故选C.
19.某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位,节目乙不能排在第一位,节目丙必须排在最后一位,则该台晚会节目演出顺序的编排方案共有 ( )
A.36种 B.42种 C.48种 D.54种
【答案】 B
【解析】分两类:一类为甲排在第一位共有=24(种),
另一类甲排在第二位共有=18(种),
故编排方案共有24+18=42(种).故选B.
20.现安排甲、乙、丙、丁、戊5名同学参加上海世博会志愿者服务活动,每人从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加。甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是( )
A.152 B.126 C.90 D.54
【答案】 B
【解析】由于五个人从事四项工作,而每项工作至少一人,那么每项工作至多两人,因为甲、乙不会开车,所以只能先安排司机,分两类:
(1)先从丙、丁、戊三人中任选一人开车;再从其余四人中任选两人作为一个元素同其他两人从事其他三项工作,共有(种);
(2)先从丙、丁、戊三人中任选两人开车:其余三人从事其他三项工作,共有(种).
所以不同安排方案的种数是+=126(种).故选B.
21.从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有 种不同的选法(用数字作答).
【答案】 660
【解析】分两步:
第一步,选出4人,由于至少1名女生,故有-=55(种)不同的选法;
第二步,从4人中选出队长、副队长各一人,有=12(种)不同的选法,
根据分步乘法计数原理共有55×12=660(种)不同的选法.
22.10件产品中有7件正品,3件次品,从中任取4件,则恰好取到1件次品的概率是 .
【答案】
【解析】从10件产品中任取4件共有=210(种)不同取法.
因为10件产品中有7件正品,3件次品,
所以从中任取4件恰好取到1件次品共有=105(种)不同的取法,
故所求的概率为P==.
23.将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少一张,如果分给同一人的两张参观券连号,那么不同的分法种数是 .
【答案】 96
【解析】5张参观券分成4堆,有2个联号有4种分法,每种分法分给4个人有种方法,所以总共有4=96(种).
24.将A,B,C,D,E,F六个字母排成一排,且A,B均在C的同侧,则不同的排法共有 种(用数字作答).
【答案】 480
【解析】第一类,字母C排在左边第一个位置,有(种);
第二类,字母C排在左边第二个位置,有(种);
第三类,字母C排在左边第三个位置,有+(种),
由对称性可知共有2×(+++)=480(种).
同课章节目录
