2023年高考数学客观题专题七 三角函数与解三角形 课件(共70张PPT)
文档属性
| 名称 | 2023年高考数学客观题专题七 三角函数与解三角形 课件(共70张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 12:27:03 | ||
图片预览






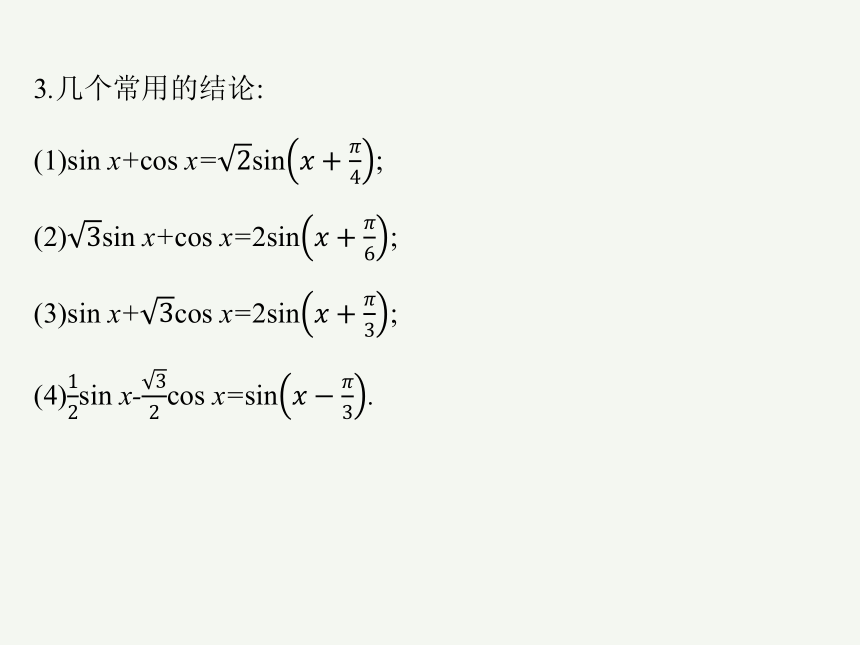


文档简介
(共70张PPT)
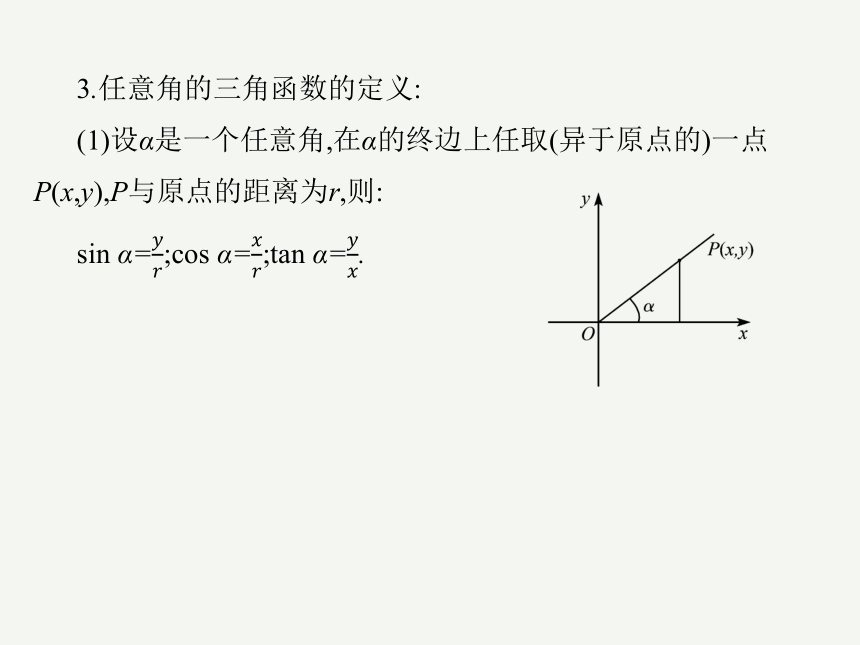
专题七 三角函数与解三角形
【考试内容】 角的概念的推广;弧度制;任意角的三角函数;单位圆中的三角函数线;同角三角函数的基本关系式;正弦、余弦的诱导公式;两角和与差的正弦、余弦、正切;二倍角的正弦、余弦、正切;正弦函数、余弦函数的图象和性质;周期函数;函数y=Asin(ωx+φ)的图象;正切函数的图象和性质;已知三角函数值求角;正弦定理;余弦定理;解斜三角形
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 15 15 15 15 5 15 20
全国卷(乙卷) 15 10 15 15 10 15 5
新高考全国Ⅰ卷 10 5
新高考全国Ⅱ卷 10
重要考点回顾
一、基本知识
1.角度制与弧度制的互化
1 rad=≈57.30°=57°18';
1°=≈0.01745(rad);π rad=180°.
2.弧长公式:l=|α|·r.
扇形面积公式:S扇形=lr=|α|·r2.
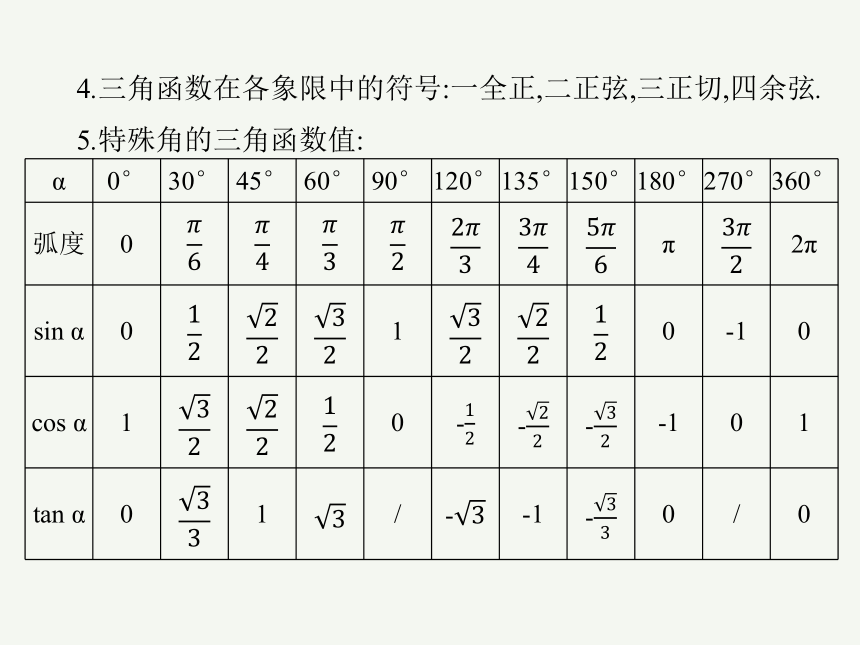
3.任意角的三角函数的定义:
(1)设α是一个任意角,在α的终边上任取(异于原点的)一点P(x,y),P与原点的距离为r,则:
sin α=;cos α=;tan α=.
(2)单位圆定义法:如图,设α是一个任意角,它的终边与单位圆交于点P(x,y),
那么:y叫做α的正弦,记作sin α,即sin α=y;x叫做α的余弦,记作cos α,即cos α=x;
叫做α的正切,记作tan α,即tan α=(x≠0).
4.三角函数在各象限中的符号:一全正,二正弦,三正切,四余弦.
5.特殊角的三角函数值:
α 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°
弧度 0 π 2π
sin α 0 1 0 -1 0
cos α 1 0 - - - -1 0 1
tan α 0 1 / - -1 - 0 / 0
6.同角三角函数的基本关系式
(1)平方关系:sin2θ+cos2θ=1;
(2)倒数关系:tan θ=.
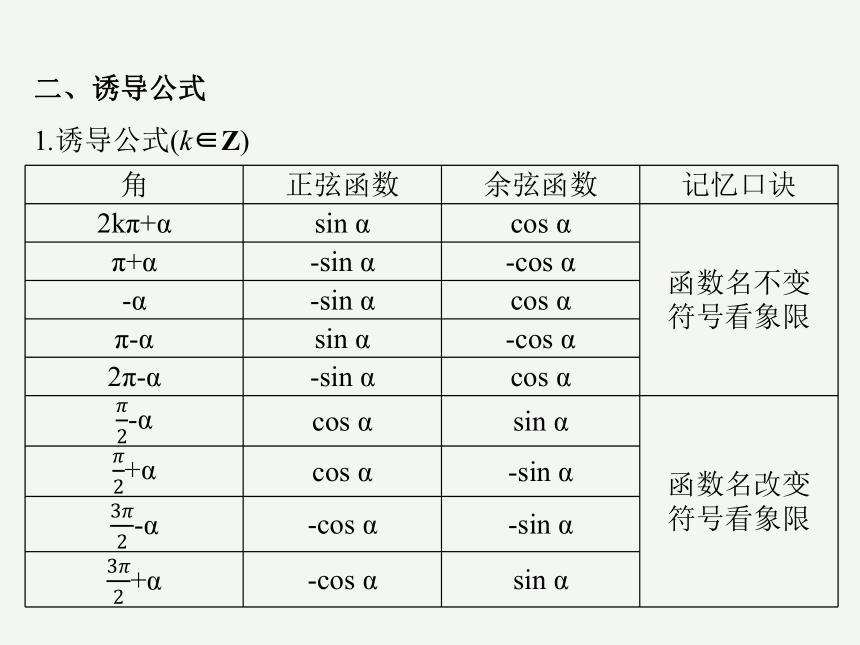
二、诱导公式
1.诱导公式(k∈Z)
角 正弦函数 余弦函数 记忆口诀
2kπ+α sin α cos α 函数名不变
符号看象限
π+α -sin α -cos α
-α -sin α cos α
π-α sin α -cos α
2π-α -sin α cos α
-α cos α sin α 函数名改变
符号看象限
+α cos α -sin α
-α -cos α -sin α
+α -cos α sin α
2.求任意角的三角函数值的问题,都可以通过诱导公式化为锐角三角函数的求值问题,具体步骤为“负角化正角”→“正角化锐角”→求值.
3.诱导公式解决常见题型
(1)求值:已知一个角的某个三角函数值,求这个角的其他三角函数值;
(2)化简:要求是能求值则求值,次数、种类尽量少,尽量化去根式,尽可能不含分母.
三、两角和与差及二倍角的三角函数
1.两角和与差的三角函数公式
sin(α±β)=sin αcos β±cos αsin β;
cos(α±β)=cos αcos β sin αsin β;
tan(α±β)= .
2.二倍角公式
sin 2α=2sin αcos α;tan 2α=;
cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α.
3.几个常用的结论:
(1)sin x+cos x=sin;
(2)sin x+cos x=2sin;
(3)sin x+cos x=2sin;
(4)sin x-cos x=sin.
四、三角函数的图象与性质
1.结合五点法作图画出正弦函数y=sin x(x∈R)、余弦函数y=cos x(x∈R)的图象.
(1)定义域:都是R.
(2)值域:都是[-1,1].
对于y=sin x,当x=+2kπ(k∈Z)时,y取最大值1;
当x=-+2kπ(k∈Z)时,y取最小值-1;
对于y=cos x,当x=2kπ(k∈Z)时,y取最大值1,
当x=π+2kπ(k∈Z)时,y取最小值-1.
(3)周期性:
①y=sin x,y=cos x 的最小正周期都是2π;
②f(x)=Asin(ωx+φ)和f(x)=Acos(ωx+φ)的最小正周期都是.
(4)单调性:
y=sin x在区间(k∈Z)上单调递增,
在(k∈Z)上单调递减;
y=cos x在区间[-π+2kπ,2kπ](k∈Z)上单调递增,
在区间[2kπ,π+2kπ](k∈Z)上单调递减.
(5)奇偶性与对称性:
正弦函数y=sin x(x∈R)是奇函数,对称中心是(kπ,0)(k∈Z),对称轴是直线x=kπ+(k∈Z);
余弦函数y=cos x(x∈R)是偶函数,对称中心是(k∈Z),对称轴是直线x=kπ(k∈Z).
2.正切函数y=tan x的图象和性质:
(1)定义域:.
(2)值域是R,在定义域上无最大值也无最小值;
(3)周期性:T=π;
(4)奇偶性与对称性:奇函数,对称中心是(k∈Z);
(5)单调性:正切函数在开区间(k∈Z)内都是增函数.
3.函数y=Asin(ωx+φ)图象的画法:
①“五点法”——设X=ωx+φ,令X=0,,π,,2π求出相应的x值,计算得出五点的坐标,描点后得出图象;
②图象变换法:这是作函数简图常用方法.
4.函数y=Asin(ωx+φ)+k的图象与y=sin x图象间的关系:
①将函数y=sin x的图象向左(φ>0)或向右(φ<0)平移|φ|个单位得y=sin(x+φ)的图象;
②函数y=sin(x+φ)图象的纵坐标不变,横坐标变为原来的,得到函数y=sin(ωx+φ)的图象;
③函数y=sin(ωx+φ)图象的横坐标不变,纵坐标变为原来的A倍,得到函数y=Asin(ωx+φ)的图象;
④将函数y=Asin(ωx+φ)的图象向上(k>0)或向下(k<0)平移|k|个单位,得到y=Asin(ωx+φ)+k的图象.
要特别注意,若由y=sin(ωx)得到y=sin(ωx+φ)的图象,则向左或向右平移||个单位.
5.研究函数y=Asin(ωx+φ)性质的方法:类比于研究y=sin x的性质,只需将y=Asin(ωx+φ)中的ωx+φ看成y=sin x中的x,但在求y=Asin(ωx+φ)的单调区间时,要特别注意A和ω的符号,通过诱导公式先将ω化正.
五、正弦、余弦定理,面积定理
1.正弦定理
===2R.
2.余弦定理
(1)a2=b2+c2-2bccos A;b2=c2+a2-2cacos B;c2=a2+b2-2abcos C.
(2)cos A=;cos B=;cos C=
3.面积定理
(1)S=aha=bhb=chc(ha,hb,hc分别表示a,b,c边上的高).
(2)S=absin C=bcsin A=casin B.
考点训练
1.点A(sin 2015°,cos 2015°)位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【答案】C
【解析】2015°-5×360°=215°,
sin 215°<0,cos 215°<0.
故选C.
2.已知角θ的顶点与坐标原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则cos= ( )
A.- B.- C. D.
【答案】D
【解析】因为直线y=2x经过一、三象限,在第一象限取特殊点(1,2),代入cos θ=,sin θ=可得cos θ=,sin θ=,
则cos=sin 2θ=.
同理,取第三象限特殊点也可得到此结论.故选D.
3.若cos α=-,且角α的终边经过点P(x,2),则P点的横坐标x= .
【答案】-2
【解析】由cos α==-,可得x=±2,
且由cos α<0可知x=-2.
4.已知角α∈,tan α=2,则cos α= .
【答案】-
【解析】π<α<,cos α<0,tan α==2,
将sin α=2cos α代入sin2α+cos2α=1即可.
5.已知α为第二象限的角,sin α=,则tan 2α= .
【答案】-
【解析】由sin2α+cos2α=1且α为第二象限角,可得cos α=-,
则tan α=-,代入tan 2α=即可.
6.设sin=,则sin 2θ= ( )
A.- B. C. D.
【答案】A
【解析】1-2sin 2=cos=-sin 2θ=,
则sin 2θ=-.
故选A.
7.若sin=,则cos= ( )
A.- B. C.- D.
【答案】A
【解析】1-2sin2=cos=,
cos=-cos=-.
故选A.
8.已知sin 2α=,则cos2= ( )
A. B. C. D.
【答案】B
【解析】2cos2-1=cos=-sin 2α=-,
可得cos2=.故选B.
【答案】A
【解析】=2,分子分母同时除以cos α,
得到=2,解得tan α=1.
故选A.
9.若=2,则tan α= ( )
A.1 B.-1 C. D.-
10.函数y=Asin(ωx+φ)的部分图象如下图所示,则其解析式可以
是 ( )
A.y=3sin B.y=-3sin
C.y=3sin D.y=-3sin
【答案】B
【解析】由图象易知,当x=0时,y<0,经验证可排除A,C.
因为点在函数图象上,将点代入y=-3sin,可知等式成立,
而将点代入y=-3sin,可知等式不成立.故选B.
11.函数f(x)=cos2-cos2(x∈R)是 ( )
A.周期为π的奇函数 B.周期为π的偶函数
C.周期为2π的奇函数 D.周期为2π的偶函数
【答案】A
【解析】函数f(x)=cos2-cos2可化为
f(x)=cos2-cos2=cos2-sin2
=cos2=cos=sin 2x,
于是可知原函数f(x)是周期为π的奇函数.故选A.
12.函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为 ( )
A.(k∈Z) B.(k∈Z)
C.(k∈Z) D.(k∈Z)
【答案】D
【解析】由五点作图知
解得ω=π,φ=,所以f(x)=cos.
令2kπ<πx+<2kπ+π,k∈Z,解得2k-故单调递减区间为,k∈Z.故选D.
13.函数y=2cos2-1是 ( )
A.最小正周期为π的奇函数 B.最小正周期为π的偶函数
C.最小正周期为的奇函数 D.最小正周期为的偶函数
【答案】A
【解析】
因为y=2cos2-1=cos2=cos=sin 2x,
所以函数f(x)是奇函数,最小正周期为T===π.故选A.
14.函数f(x)=sin 2x-4sin xcos3x(x∈R)的最小正周期为 .
【答案】
【解析】f(x)=2sin xcos x-4sin xcos3x=2sin xcos x(1-2cos2x)
=-sin 2xcos 2x=-sin 4x,
可得T=.
15.现有四个函数:①y=xsin x,②y=xcos x,③y=x|cos x|,④y=x·2x的部分图象如下,但顺序被打乱了,则按从左到右将图象对应函数序号排列正确的是 ( )
A.①②③④ B.②①③④
C.③①④② D.①④②③
【答案】D
【解析】由奇偶性可知④为非奇非偶函数,故④的图象只有第二个图满足条件.故选D.
16.在函数①y=cos|2x|,②y=|cos x|,③y=cos,
④y=tan中,最小正周期为π的所有函数为 ( )
A.①②③ B.①③④ C.②④ D.①③
【答案】A
【解析】由y=cos x是偶函数可知y=cos|2x|=cos 2x,最小正周期为π,即①正确;
y=|cos x|的最小正周期也为π,即②也正确;
y=cos最小正周期为π,即③正确;
y=tan的最小正周期为,即④错误.故选A.
17.若函数y=3cos(2x+φ)的图象关于点中心对称,那么|φ|的最小值为 ( )
A. B. C. D.
【答案】A
【解析】3cos=3cos=0,
则由+φ=kπ+(k∈Z)可得φ=kπ-(k∈Z),
所以当k=2时,=.故选A.
【答案】A
【解析】由于函数y=sin的图象的对称轴方程是2x+=+kπ(k∈Z),即x=-π+(k∈Z).
易知,当k=1时有x=-.故选A.
18.函数y=sin的图象的一条对称轴方程是 ( )
A.x=- B.x=- C.x= D.x=
19.已知ω>0,0<φ<π,直线x=和x=是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,则φ= ( )
A. B. C. D.
【答案】A
【解析】由题意得=-=π,T=2π,ω=1用代入法即可.
20.设函数f(x)=sin+cos,则 ( )
A.y=f(x)在单调递增,其图象关于直线x=对称
B.y=f(x)在单调递增,其图象关于直线x=对称
C.y=f(x)在单调递减,其图象关于直线x=对称
D.y=f(x)在单调递减,其图象关于直线x=对称
【答案】D
【解析】依题意得f(x)=sin+cos=cos 2x.
故选D.
21.函数f(x)=sin(x+φ)-2sin φcos x的最大值为 .
【答案】1
【解析】f(x)=sin xcos φ+cos xsin φ-2cos xsin φ=sin(x-φ),
则f(x)max=1.
22.设当x=θ时,函数f(x)=sin x-2cos x取得最大值,则cos θ= .
【答案】-
【解析】f(x)=sin(x-φ),其中cos φ=,sin φ=,
当x-φ=2kπ+(k∈Z)时取最大值.cos θ=cos=-sin φ=-.
23.已知平面向量a=(sin2x,cos2x),b=(sin2x,-cos2x),函数f(x)=a·b+4cos2x+2sin xcos x.若存在m∈R使f(x)≥f(m)在R上恒成立,则f(m)= .
【答案】0
【解析】∵f(x)=sin4x-cos4x+4cos2x+2sin xcos x
=-cos 2x+2(1+cos 2x)+sin 2x
=cos 2x+sin 2x+2
=2sin+2≥0,
∴f(m)=0.
24.函数f(x)=Asin(ωx+φ)的部分图象如图所示,则将y=f(x)的图象向右平移个单位后,得到的图象的函数解析式为 ( )
A.y=sin 2x B.y=cos 2x
C.y=sin D.y=sin
【答案】D
【解析】由函数的图象可知,A=1,且T=-=,所以有T=π.
又由T==π,得ω=2.
又因点在函数图象上,所以有f=sin=1.
因为|φ|<,则φ=.于是f(x)=sin.
将y=f(x)的图象向右平移个单位,
得y=f=sin=sin.故选D.
25.函数y=f(x)的图象沿x轴向左平移个单位,沿y轴向下平移1个单位,再把图象上每个点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=sin x的图象,则y=f(x)的解析式为 ( )
A.y=sin+1 B.y=sin+1
C.y=sin-1 D.y=sin-1
【答案】B
【解析】由题意可知,将函数y=sin x的图象的变化倒推回去,即可求得f(x)的解析式.
首先将y=sin x的图象上每个点的横坐标缩短为原来的(纵坐标不变),得到函数y=sin 2x的图象;
再将y=sin 2x的图象沿y轴向上平移1个单位,得到函数y=sin 2x+1的图象;
再将函数y=sin 2x+1的图象沿x轴向右平移个单位,得到函数y=sin+1的图象.故选B.
26.为得到函数y=cos 2x的图象,可把函数y=sin图象上所有点 ( )
A.向右平移个单位 B.向右平移个单位
C.向左平移个单位 D.向左平移个单位
【答案】C
【解析】可使用代入法.
27.设函数f(x)=cos ωx(ω>0),将y=f(x)的图象向右平移个单位长度后,所得的图象与原图象重合,则ω的最小值等于 ( )
A. B.3 C.6 D.9
【答案】C
【解析】由题意将y=f(x)的图象向右平移个单位长度后,所得的图象与原图象重合,说明是此函数周期的整数倍,得·k=(k∈Z),解得ω=6k,又ω>0,令k=1,得ωmin=6.故选C.
28.函数y=cos(2x+φ)(-π≤φ<π)的图象向右平移个单位后,与函数y=sin的图象重合,则φ= .
【答案】
【解析】将函数向右平移个单位得,y=cos
=cos(2x-π+φ)=sin=sin,
而它与函数y=sin的图象重合.
令2x+φ-=2x++2kπ,k∈Z,得φ=+2kπ,k∈Z.∴φ=.
29.将函数f(x)=cos x-sin x(x∈R)的图象向左平移φ(φ>0)个单位长度后,所得图象关于原点对称,则φ的最小值是 ( )
A. B. C. D.
【答案】B
【解析】函数f(x)=cos x-sin x=2cos,将函数图象向左平移得到g(x)=2cos的图象关于原点对称,则φ+=kπ+.当k=0时,φmin=.故选B.
30.已知△ABC中,a=,b=,B=60°,那么角A等于 ( )
A.135° B.90° C.45° D.30°
【答案】C
【解析】∵=,∴sin A===.
∵A∈(0°,180°)且A∴A=45°.故选C.
31.在△ABC中,A,B,C所对的边长分别是a,b,c,且A=,a=,b=1,则c= ( )
A.1 B.2 C.-1 D.
【答案】B
【解析】∵=,∴sin B===.
∵B∈(0,π)且A>B,∴B=,C=.
利用勾股定理得c==2.故选B.
32.在△ABC中,AB=3,BC=,AC=4,则△ABC的面积是 ( )
A.3 B. C.3 D.6
【答案】C
【解析】∵cos A===,则sin A=.
∴S△ABC=·AB·AC·=×3×4×=3.故选C.
33.已知a,b,c分别为△ABC的内角A,B,C所对的边,且
(b-c)(sin B+sin C)=(a-c)·sin A,则角B的大小为 ( )
A.30° B.45° C.60° D.120°
【答案】A
【解析】∵由正弦定理,可得(b-c)(b+c)=a(a-c),
有b2-c2=a2-ac,则cos B=.
由于034.已知a,b,c分别为△ABC的三个内角A,B,C所对的边,b=2,B=,
C=,则△ABC的面积为( )
A.2+2 B.+1 C.2-2 D.-1
【答案】B
【解析】A=π-=,由正弦定理得=,
则a===+,
∴S△ABC=absin C=×2×(+)×=+1.故选B.
35.锐角三角形ABC中,a,b,c是角A,B,C所对的边,且(a2+c2-b2)·tan B
=ac,则B= .
【答案】60°
【解析】∵cos B===,
∴2tan B·cos B=,即sin B=.
∵△ABC为锐角三角形,
∴B=60°.
36.若△ABC的内角A满足sin 2A=,则sin A+cos A= ( )
A. B. C.- D.±
【答案】B
【解析】(sin A+cos A)2=sin2A+2sin Acos A+cos2A=.
因为A是△ABC的内角,且sin 2A>0,则0<2A<π,0于是sin A>0,cos A>0,所以sin A+cos A=.故选B.
37.如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角 ∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100 m,则山高MN= m.
【答案】150
【解析】在直角三角形ABC 中,由条件可得AC=100,
在△MAC 中,由正弦定理可得=,
故AM= AC=100.
在直角三角形MAN 中,MN=AM·sin 60°=150.
38.在△ABC中,角A,B,C所对的边长分别为a,b,c,且满足
csin A=acos C,则sin A+sin B的最大值是 ( )
A.1 B. C.3 D.
【答案】D
【解析】由正弦定理可得,2Rsin Csin A=·2Rsin Acos C,
则tan C=,C=,
则sin A+sin B=sin A+sin=sin.故选D.
39.在△ABC中,角B=,BC边上的高等于BC,则sin A= ( )
A. B. C. D.
【答案】D
【解析】设BC边上的高线为AD,则BC=3AD.
又B=,则BD=AD,故DC=2AD,所以AC==AD.
由正弦定理,知=,即=,解得sin A=.故选D.
40.(多选题)已知函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)的部分图象与y轴交于点,与x轴的一个交点为(1,0),如图所示,则下列说法正确的是 ( )
A.φ=
B.f(x)的最小正周期为6
C.y=f(x)的图象关于直线x=对称
D.f(x)在单调递减
【答案】ABC
【解析】对于A,由函数f(x)=cos(ωx+φ)的图象与y轴交于点,
所以cos φ=.又0<φ<π,所以φ=,故A正确;
对于B,由f(x)的图象与x轴的一个交点为(1,0),
即y=f(1)=0,所以ω+=2kπ+,k∈Z;
又1<<2,解得<ω<,所以ω=;
所以f(x)=cos,求得f(x)的最小正周期为T=6,故B正确;
【解析】对于C,f=cos=-1,
所以x=是f(x)的一条对称轴,故C正确;
对于D,令2kπ≤x+≤2kπ+π,k∈Z,解得6k-≤x≤6k+,k∈Z,
所以函数f(x)在,k∈Z上单调递减,故D错误.
故选ABC.
41.(多选题)已知ω>0,函数f(x)=sin的图象在区间上有且仅有一条对称轴,则实数ω的可能取值是 ( )
A.1 B.2 C.3 D.4
【答案】AB
【解析】函数f(x)=sin的图象在区间上有且仅有一条对称轴,则函数的最小正周期T≥2=π.
所以当ω=1时,T=2π满足条件;当ω=2时,T=π满足条件;
当ω=3时,T=不满足条件;当ω=4时,T=不满足条件.
故选AB.
42.(多选题)为了得到函数y=cos的图象,可作如下变换( )
A.将y=cos x的图象上所有点向左平移个单位长度,然后将所得图象上所有点的横坐标变为原来的,纵坐标不变而得到
B.将y=cos x的图象上所有点向右平移个单位长度,然后将所得图象上所有点的横坐标变为原来的2倍,纵坐标不变而得到
C.将y=cos x的图象上所有点的横坐标变为原来的,纵坐标不变,然后将所得图象上所有点向左平移个单位长度而得到
D.将y=cos x的图象上所有点的横坐标变为原来的,纵坐标不变,然后将所得图象上所有点向左平移个单位长度而得到
【答案】AD
【解析】为了得到函数y=cos的图象,
将y=cos x的图象上所有点向左平移个单位长度,然后将所得图象上所有点的横坐标变为原来的,纵坐标不变而得到.
也可将y=cos x的图象上所有点的横坐标变为原来的,纵坐标不变,然后将所得图象上所有点向左平移个单位长度而得.
故选AD.
43.(多选题)已知函数f(x)=sin(ωx+φ)-cos(ωx+φ)
的最小正周期为π,且f=2,则下列说法正确的是 ( )
A.f(x)是奇函数
B.f(x)的图象关于直线x=对称
C.f(x)的图象关于点对称
D.f(x)在上是增函数
【答案】ABD
【解析】f(x)=sin(ωx+φ)-cos(ωx+φ)=2sin.
∵f(x)的最小正周期为π,∴ω==2.∴f(x)=2sin.
∵f=2,∴2sin=2,解得φ=+2kπ,k∈Z.
∵0<φ<,∴φ=.∴f(x)=2sin 2x.
∴f(x)是奇函数,故A正确;其对称轴方程为x=+,k∈Z,故B正确;
其对称中心为,k∈Z,故C错误;
单调递增区间为,k∈Z,故D正确.
故选ABD.
44.(多选题)将函数y=cos x的图象向左平移个单位,得到函数y=f(x)的图象,则下列说法正确的是 ( )
A.y=f(x)是奇函数
B.y=f(x)的周期是π
C.y=f(x)的图象关于直线x=对称
D.y=f(x)的图象关于点对称
【答案】AC
【解析】将函数y=cos x的图象向左平移个单位,得到函数y=f(x)=cos=sin x的图象.
显然,f(x)是奇函数,故A正确;
由于f(x)的最小正周期为2π,故B不正确;
当x=时,f(x)取得最大值,故y=f(x)的图象关于直线x=对称,故C正确;
当x=-时,f(x)取得最小值,故y=f(x)的图象不关于点对称,故D错误.
故选AC.
45.(多选题)如图是函数y=sin(ωx+φ)的部分图象,则sin(ωx+φ)=( )
A.sin B.sin
C.cos D.cos
【答案】BC
【解析】由图象知函数的周期T=2×=π,即=π,即ω=2,
由五点作图法得2×+φ=π,解得φ=,
则f(x)=sin=cos=cos
=cos=sin=sin.
故选BC.
专题七 三角函数与解三角形
【考试内容】 角的概念的推广;弧度制;任意角的三角函数;单位圆中的三角函数线;同角三角函数的基本关系式;正弦、余弦的诱导公式;两角和与差的正弦、余弦、正切;二倍角的正弦、余弦、正切;正弦函数、余弦函数的图象和性质;周期函数;函数y=Asin(ωx+φ)的图象;正切函数的图象和性质;已知三角函数值求角;正弦定理;余弦定理;解斜三角形
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 15 15 15 15 5 15 20
全国卷(乙卷) 15 10 15 15 10 15 5
新高考全国Ⅰ卷 10 5
新高考全国Ⅱ卷 10
重要考点回顾
一、基本知识
1.角度制与弧度制的互化
1 rad=≈57.30°=57°18';
1°=≈0.01745(rad);π rad=180°.
2.弧长公式:l=|α|·r.
扇形面积公式:S扇形=lr=|α|·r2.
3.任意角的三角函数的定义:
(1)设α是一个任意角,在α的终边上任取(异于原点的)一点P(x,y),P与原点的距离为r,则:
sin α=;cos α=;tan α=.
(2)单位圆定义法:如图,设α是一个任意角,它的终边与单位圆交于点P(x,y),
那么:y叫做α的正弦,记作sin α,即sin α=y;x叫做α的余弦,记作cos α,即cos α=x;
叫做α的正切,记作tan α,即tan α=(x≠0).
4.三角函数在各象限中的符号:一全正,二正弦,三正切,四余弦.
5.特殊角的三角函数值:
α 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°
弧度 0 π 2π
sin α 0 1 0 -1 0
cos α 1 0 - - - -1 0 1
tan α 0 1 / - -1 - 0 / 0
6.同角三角函数的基本关系式
(1)平方关系:sin2θ+cos2θ=1;
(2)倒数关系:tan θ=.
二、诱导公式
1.诱导公式(k∈Z)
角 正弦函数 余弦函数 记忆口诀
2kπ+α sin α cos α 函数名不变
符号看象限
π+α -sin α -cos α
-α -sin α cos α
π-α sin α -cos α
2π-α -sin α cos α
-α cos α sin α 函数名改变
符号看象限
+α cos α -sin α
-α -cos α -sin α
+α -cos α sin α
2.求任意角的三角函数值的问题,都可以通过诱导公式化为锐角三角函数的求值问题,具体步骤为“负角化正角”→“正角化锐角”→求值.
3.诱导公式解决常见题型
(1)求值:已知一个角的某个三角函数值,求这个角的其他三角函数值;
(2)化简:要求是能求值则求值,次数、种类尽量少,尽量化去根式,尽可能不含分母.
三、两角和与差及二倍角的三角函数
1.两角和与差的三角函数公式
sin(α±β)=sin αcos β±cos αsin β;
cos(α±β)=cos αcos β sin αsin β;
tan(α±β)= .
2.二倍角公式
sin 2α=2sin αcos α;tan 2α=;
cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α.
3.几个常用的结论:
(1)sin x+cos x=sin;
(2)sin x+cos x=2sin;
(3)sin x+cos x=2sin;
(4)sin x-cos x=sin.
四、三角函数的图象与性质
1.结合五点法作图画出正弦函数y=sin x(x∈R)、余弦函数y=cos x(x∈R)的图象.
(1)定义域:都是R.
(2)值域:都是[-1,1].
对于y=sin x,当x=+2kπ(k∈Z)时,y取最大值1;
当x=-+2kπ(k∈Z)时,y取最小值-1;
对于y=cos x,当x=2kπ(k∈Z)时,y取最大值1,
当x=π+2kπ(k∈Z)时,y取最小值-1.
(3)周期性:
①y=sin x,y=cos x 的最小正周期都是2π;
②f(x)=Asin(ωx+φ)和f(x)=Acos(ωx+φ)的最小正周期都是.
(4)单调性:
y=sin x在区间(k∈Z)上单调递增,
在(k∈Z)上单调递减;
y=cos x在区间[-π+2kπ,2kπ](k∈Z)上单调递增,
在区间[2kπ,π+2kπ](k∈Z)上单调递减.
(5)奇偶性与对称性:
正弦函数y=sin x(x∈R)是奇函数,对称中心是(kπ,0)(k∈Z),对称轴是直线x=kπ+(k∈Z);
余弦函数y=cos x(x∈R)是偶函数,对称中心是(k∈Z),对称轴是直线x=kπ(k∈Z).
2.正切函数y=tan x的图象和性质:
(1)定义域:.
(2)值域是R,在定义域上无最大值也无最小值;
(3)周期性:T=π;
(4)奇偶性与对称性:奇函数,对称中心是(k∈Z);
(5)单调性:正切函数在开区间(k∈Z)内都是增函数.
3.函数y=Asin(ωx+φ)图象的画法:
①“五点法”——设X=ωx+φ,令X=0,,π,,2π求出相应的x值,计算得出五点的坐标,描点后得出图象;
②图象变换法:这是作函数简图常用方法.
4.函数y=Asin(ωx+φ)+k的图象与y=sin x图象间的关系:
①将函数y=sin x的图象向左(φ>0)或向右(φ<0)平移|φ|个单位得y=sin(x+φ)的图象;
②函数y=sin(x+φ)图象的纵坐标不变,横坐标变为原来的,得到函数y=sin(ωx+φ)的图象;
③函数y=sin(ωx+φ)图象的横坐标不变,纵坐标变为原来的A倍,得到函数y=Asin(ωx+φ)的图象;
④将函数y=Asin(ωx+φ)的图象向上(k>0)或向下(k<0)平移|k|个单位,得到y=Asin(ωx+φ)+k的图象.
要特别注意,若由y=sin(ωx)得到y=sin(ωx+φ)的图象,则向左或向右平移||个单位.
5.研究函数y=Asin(ωx+φ)性质的方法:类比于研究y=sin x的性质,只需将y=Asin(ωx+φ)中的ωx+φ看成y=sin x中的x,但在求y=Asin(ωx+φ)的单调区间时,要特别注意A和ω的符号,通过诱导公式先将ω化正.
五、正弦、余弦定理,面积定理
1.正弦定理
===2R.
2.余弦定理
(1)a2=b2+c2-2bccos A;b2=c2+a2-2cacos B;c2=a2+b2-2abcos C.
(2)cos A=;cos B=;cos C=
3.面积定理
(1)S=aha=bhb=chc(ha,hb,hc分别表示a,b,c边上的高).
(2)S=absin C=bcsin A=casin B.
考点训练
1.点A(sin 2015°,cos 2015°)位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【答案】C
【解析】2015°-5×360°=215°,
sin 215°<0,cos 215°<0.
故选C.
2.已知角θ的顶点与坐标原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则cos= ( )
A.- B.- C. D.
【答案】D
【解析】因为直线y=2x经过一、三象限,在第一象限取特殊点(1,2),代入cos θ=,sin θ=可得cos θ=,sin θ=,
则cos=sin 2θ=.
同理,取第三象限特殊点也可得到此结论.故选D.
3.若cos α=-,且角α的终边经过点P(x,2),则P点的横坐标x= .
【答案】-2
【解析】由cos α==-,可得x=±2,
且由cos α<0可知x=-2.
4.已知角α∈,tan α=2,则cos α= .
【答案】-
【解析】π<α<,cos α<0,tan α==2,
将sin α=2cos α代入sin2α+cos2α=1即可.
5.已知α为第二象限的角,sin α=,则tan 2α= .
【答案】-
【解析】由sin2α+cos2α=1且α为第二象限角,可得cos α=-,
则tan α=-,代入tan 2α=即可.
6.设sin=,则sin 2θ= ( )
A.- B. C. D.
【答案】A
【解析】1-2sin 2=cos=-sin 2θ=,
则sin 2θ=-.
故选A.
7.若sin=,则cos= ( )
A.- B. C.- D.
【答案】A
【解析】1-2sin2=cos=,
cos=-cos=-.
故选A.
8.已知sin 2α=,则cos2= ( )
A. B. C. D.
【答案】B
【解析】2cos2-1=cos=-sin 2α=-,
可得cos2=.故选B.
【答案】A
【解析】=2,分子分母同时除以cos α,
得到=2,解得tan α=1.
故选A.
9.若=2,则tan α= ( )
A.1 B.-1 C. D.-
10.函数y=Asin(ωx+φ)的部分图象如下图所示,则其解析式可以
是 ( )
A.y=3sin B.y=-3sin
C.y=3sin D.y=-3sin
【答案】B
【解析】由图象易知,当x=0时,y<0,经验证可排除A,C.
因为点在函数图象上,将点代入y=-3sin,可知等式成立,
而将点代入y=-3sin,可知等式不成立.故选B.
11.函数f(x)=cos2-cos2(x∈R)是 ( )
A.周期为π的奇函数 B.周期为π的偶函数
C.周期为2π的奇函数 D.周期为2π的偶函数
【答案】A
【解析】函数f(x)=cos2-cos2可化为
f(x)=cos2-cos2=cos2-sin2
=cos2=cos=sin 2x,
于是可知原函数f(x)是周期为π的奇函数.故选A.
12.函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为 ( )
A.(k∈Z) B.(k∈Z)
C.(k∈Z) D.(k∈Z)
【答案】D
【解析】由五点作图知
解得ω=π,φ=,所以f(x)=cos.
令2kπ<πx+<2kπ+π,k∈Z,解得2k-
13.函数y=2cos2-1是 ( )
A.最小正周期为π的奇函数 B.最小正周期为π的偶函数
C.最小正周期为的奇函数 D.最小正周期为的偶函数
【答案】A
【解析】
因为y=2cos2-1=cos2=cos=sin 2x,
所以函数f(x)是奇函数,最小正周期为T===π.故选A.
14.函数f(x)=sin 2x-4sin xcos3x(x∈R)的最小正周期为 .
【答案】
【解析】f(x)=2sin xcos x-4sin xcos3x=2sin xcos x(1-2cos2x)
=-sin 2xcos 2x=-sin 4x,
可得T=.
15.现有四个函数:①y=xsin x,②y=xcos x,③y=x|cos x|,④y=x·2x的部分图象如下,但顺序被打乱了,则按从左到右将图象对应函数序号排列正确的是 ( )
A.①②③④ B.②①③④
C.③①④② D.①④②③
【答案】D
【解析】由奇偶性可知④为非奇非偶函数,故④的图象只有第二个图满足条件.故选D.
16.在函数①y=cos|2x|,②y=|cos x|,③y=cos,
④y=tan中,最小正周期为π的所有函数为 ( )
A.①②③ B.①③④ C.②④ D.①③
【答案】A
【解析】由y=cos x是偶函数可知y=cos|2x|=cos 2x,最小正周期为π,即①正确;
y=|cos x|的最小正周期也为π,即②也正确;
y=cos最小正周期为π,即③正确;
y=tan的最小正周期为,即④错误.故选A.
17.若函数y=3cos(2x+φ)的图象关于点中心对称,那么|φ|的最小值为 ( )
A. B. C. D.
【答案】A
【解析】3cos=3cos=0,
则由+φ=kπ+(k∈Z)可得φ=kπ-(k∈Z),
所以当k=2时,=.故选A.
【答案】A
【解析】由于函数y=sin的图象的对称轴方程是2x+=+kπ(k∈Z),即x=-π+(k∈Z).
易知,当k=1时有x=-.故选A.
18.函数y=sin的图象的一条对称轴方程是 ( )
A.x=- B.x=- C.x= D.x=
19.已知ω>0,0<φ<π,直线x=和x=是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,则φ= ( )
A. B. C. D.
【答案】A
【解析】由题意得=-=π,T=2π,ω=1用代入法即可.
20.设函数f(x)=sin+cos,则 ( )
A.y=f(x)在单调递增,其图象关于直线x=对称
B.y=f(x)在单调递增,其图象关于直线x=对称
C.y=f(x)在单调递减,其图象关于直线x=对称
D.y=f(x)在单调递减,其图象关于直线x=对称
【答案】D
【解析】依题意得f(x)=sin+cos=cos 2x.
故选D.
21.函数f(x)=sin(x+φ)-2sin φcos x的最大值为 .
【答案】1
【解析】f(x)=sin xcos φ+cos xsin φ-2cos xsin φ=sin(x-φ),
则f(x)max=1.
22.设当x=θ时,函数f(x)=sin x-2cos x取得最大值,则cos θ= .
【答案】-
【解析】f(x)=sin(x-φ),其中cos φ=,sin φ=,
当x-φ=2kπ+(k∈Z)时取最大值.cos θ=cos=-sin φ=-.
23.已知平面向量a=(sin2x,cos2x),b=(sin2x,-cos2x),函数f(x)=a·b+4cos2x+2sin xcos x.若存在m∈R使f(x)≥f(m)在R上恒成立,则f(m)= .
【答案】0
【解析】∵f(x)=sin4x-cos4x+4cos2x+2sin xcos x
=-cos 2x+2(1+cos 2x)+sin 2x
=cos 2x+sin 2x+2
=2sin+2≥0,
∴f(m)=0.
24.函数f(x)=Asin(ωx+φ)的部分图象如图所示,则将y=f(x)的图象向右平移个单位后,得到的图象的函数解析式为 ( )
A.y=sin 2x B.y=cos 2x
C.y=sin D.y=sin
【答案】D
【解析】由函数的图象可知,A=1,且T=-=,所以有T=π.
又由T==π,得ω=2.
又因点在函数图象上,所以有f=sin=1.
因为|φ|<,则φ=.于是f(x)=sin.
将y=f(x)的图象向右平移个单位,
得y=f=sin=sin.故选D.
25.函数y=f(x)的图象沿x轴向左平移个单位,沿y轴向下平移1个单位,再把图象上每个点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=sin x的图象,则y=f(x)的解析式为 ( )
A.y=sin+1 B.y=sin+1
C.y=sin-1 D.y=sin-1
【答案】B
【解析】由题意可知,将函数y=sin x的图象的变化倒推回去,即可求得f(x)的解析式.
首先将y=sin x的图象上每个点的横坐标缩短为原来的(纵坐标不变),得到函数y=sin 2x的图象;
再将y=sin 2x的图象沿y轴向上平移1个单位,得到函数y=sin 2x+1的图象;
再将函数y=sin 2x+1的图象沿x轴向右平移个单位,得到函数y=sin+1的图象.故选B.
26.为得到函数y=cos 2x的图象,可把函数y=sin图象上所有点 ( )
A.向右平移个单位 B.向右平移个单位
C.向左平移个单位 D.向左平移个单位
【答案】C
【解析】可使用代入法.
27.设函数f(x)=cos ωx(ω>0),将y=f(x)的图象向右平移个单位长度后,所得的图象与原图象重合,则ω的最小值等于 ( )
A. B.3 C.6 D.9
【答案】C
【解析】由题意将y=f(x)的图象向右平移个单位长度后,所得的图象与原图象重合,说明是此函数周期的整数倍,得·k=(k∈Z),解得ω=6k,又ω>0,令k=1,得ωmin=6.故选C.
28.函数y=cos(2x+φ)(-π≤φ<π)的图象向右平移个单位后,与函数y=sin的图象重合,则φ= .
【答案】
【解析】将函数向右平移个单位得,y=cos
=cos(2x-π+φ)=sin=sin,
而它与函数y=sin的图象重合.
令2x+φ-=2x++2kπ,k∈Z,得φ=+2kπ,k∈Z.∴φ=.
29.将函数f(x)=cos x-sin x(x∈R)的图象向左平移φ(φ>0)个单位长度后,所得图象关于原点对称,则φ的最小值是 ( )
A. B. C. D.
【答案】B
【解析】函数f(x)=cos x-sin x=2cos,将函数图象向左平移得到g(x)=2cos的图象关于原点对称,则φ+=kπ+.当k=0时,φmin=.故选B.
30.已知△ABC中,a=,b=,B=60°,那么角A等于 ( )
A.135° B.90° C.45° D.30°
【答案】C
【解析】∵=,∴sin A===.
∵A∈(0°,180°)且A
31.在△ABC中,A,B,C所对的边长分别是a,b,c,且A=,a=,b=1,则c= ( )
A.1 B.2 C.-1 D.
【答案】B
【解析】∵=,∴sin B===.
∵B∈(0,π)且A>B,∴B=,C=.
利用勾股定理得c==2.故选B.
32.在△ABC中,AB=3,BC=,AC=4,则△ABC的面积是 ( )
A.3 B. C.3 D.6
【答案】C
【解析】∵cos A===,则sin A=.
∴S△ABC=·AB·AC·=×3×4×=3.故选C.
33.已知a,b,c分别为△ABC的内角A,B,C所对的边,且
(b-c)(sin B+sin C)=(a-c)·sin A,则角B的大小为 ( )
A.30° B.45° C.60° D.120°
【答案】A
【解析】∵由正弦定理,可得(b-c)(b+c)=a(a-c),
有b2-c2=a2-ac,则cos B=.
由于0
C=,则△ABC的面积为( )
A.2+2 B.+1 C.2-2 D.-1
【答案】B
【解析】A=π-=,由正弦定理得=,
则a===+,
∴S△ABC=absin C=×2×(+)×=+1.故选B.
35.锐角三角形ABC中,a,b,c是角A,B,C所对的边,且(a2+c2-b2)·tan B
=ac,则B= .
【答案】60°
【解析】∵cos B===,
∴2tan B·cos B=,即sin B=.
∵△ABC为锐角三角形,
∴B=60°.
36.若△ABC的内角A满足sin 2A=,则sin A+cos A= ( )
A. B. C.- D.±
【答案】B
【解析】(sin A+cos A)2=sin2A+2sin Acos A+cos2A=.
因为A是△ABC的内角,且sin 2A>0,则0<2A<π,0
37.如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角 ∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100 m,则山高MN= m.
【答案】150
【解析】在直角三角形ABC 中,由条件可得AC=100,
在△MAC 中,由正弦定理可得=,
故AM= AC=100.
在直角三角形MAN 中,MN=AM·sin 60°=150.
38.在△ABC中,角A,B,C所对的边长分别为a,b,c,且满足
csin A=acos C,则sin A+sin B的最大值是 ( )
A.1 B. C.3 D.
【答案】D
【解析】由正弦定理可得,2Rsin Csin A=·2Rsin Acos C,
则tan C=,C=,
则sin A+sin B=sin A+sin=sin.故选D.
39.在△ABC中,角B=,BC边上的高等于BC,则sin A= ( )
A. B. C. D.
【答案】D
【解析】设BC边上的高线为AD,则BC=3AD.
又B=,则BD=AD,故DC=2AD,所以AC==AD.
由正弦定理,知=,即=,解得sin A=.故选D.
40.(多选题)已知函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)的部分图象与y轴交于点,与x轴的一个交点为(1,0),如图所示,则下列说法正确的是 ( )
A.φ=
B.f(x)的最小正周期为6
C.y=f(x)的图象关于直线x=对称
D.f(x)在单调递减
【答案】ABC
【解析】对于A,由函数f(x)=cos(ωx+φ)的图象与y轴交于点,
所以cos φ=.又0<φ<π,所以φ=,故A正确;
对于B,由f(x)的图象与x轴的一个交点为(1,0),
即y=f(1)=0,所以ω+=2kπ+,k∈Z;
又1<<2,解得<ω<,所以ω=;
所以f(x)=cos,求得f(x)的最小正周期为T=6,故B正确;
【解析】对于C,f=cos=-1,
所以x=是f(x)的一条对称轴,故C正确;
对于D,令2kπ≤x+≤2kπ+π,k∈Z,解得6k-≤x≤6k+,k∈Z,
所以函数f(x)在,k∈Z上单调递减,故D错误.
故选ABC.
41.(多选题)已知ω>0,函数f(x)=sin的图象在区间上有且仅有一条对称轴,则实数ω的可能取值是 ( )
A.1 B.2 C.3 D.4
【答案】AB
【解析】函数f(x)=sin的图象在区间上有且仅有一条对称轴,则函数的最小正周期T≥2=π.
所以当ω=1时,T=2π满足条件;当ω=2时,T=π满足条件;
当ω=3时,T=不满足条件;当ω=4时,T=不满足条件.
故选AB.
42.(多选题)为了得到函数y=cos的图象,可作如下变换( )
A.将y=cos x的图象上所有点向左平移个单位长度,然后将所得图象上所有点的横坐标变为原来的,纵坐标不变而得到
B.将y=cos x的图象上所有点向右平移个单位长度,然后将所得图象上所有点的横坐标变为原来的2倍,纵坐标不变而得到
C.将y=cos x的图象上所有点的横坐标变为原来的,纵坐标不变,然后将所得图象上所有点向左平移个单位长度而得到
D.将y=cos x的图象上所有点的横坐标变为原来的,纵坐标不变,然后将所得图象上所有点向左平移个单位长度而得到
【答案】AD
【解析】为了得到函数y=cos的图象,
将y=cos x的图象上所有点向左平移个单位长度,然后将所得图象上所有点的横坐标变为原来的,纵坐标不变而得到.
也可将y=cos x的图象上所有点的横坐标变为原来的,纵坐标不变,然后将所得图象上所有点向左平移个单位长度而得.
故选AD.
43.(多选题)已知函数f(x)=sin(ωx+φ)-cos(ωx+φ)
的最小正周期为π,且f=2,则下列说法正确的是 ( )
A.f(x)是奇函数
B.f(x)的图象关于直线x=对称
C.f(x)的图象关于点对称
D.f(x)在上是增函数
【答案】ABD
【解析】f(x)=sin(ωx+φ)-cos(ωx+φ)=2sin.
∵f(x)的最小正周期为π,∴ω==2.∴f(x)=2sin.
∵f=2,∴2sin=2,解得φ=+2kπ,k∈Z.
∵0<φ<,∴φ=.∴f(x)=2sin 2x.
∴f(x)是奇函数,故A正确;其对称轴方程为x=+,k∈Z,故B正确;
其对称中心为,k∈Z,故C错误;
单调递增区间为,k∈Z,故D正确.
故选ABD.
44.(多选题)将函数y=cos x的图象向左平移个单位,得到函数y=f(x)的图象,则下列说法正确的是 ( )
A.y=f(x)是奇函数
B.y=f(x)的周期是π
C.y=f(x)的图象关于直线x=对称
D.y=f(x)的图象关于点对称
【答案】AC
【解析】将函数y=cos x的图象向左平移个单位,得到函数y=f(x)=cos=sin x的图象.
显然,f(x)是奇函数,故A正确;
由于f(x)的最小正周期为2π,故B不正确;
当x=时,f(x)取得最大值,故y=f(x)的图象关于直线x=对称,故C正确;
当x=-时,f(x)取得最小值,故y=f(x)的图象不关于点对称,故D错误.
故选AC.
45.(多选题)如图是函数y=sin(ωx+φ)的部分图象,则sin(ωx+φ)=( )
A.sin B.sin
C.cos D.cos
【答案】BC
【解析】由图象知函数的周期T=2×=π,即=π,即ω=2,
由五点作图法得2×+φ=π,解得φ=,
则f(x)=sin=cos=cos
=cos=sin=sin.
故选BC.
同课章节目录
