2023年高考数学客观题专题十一 圆锥曲线 课件(共52张PPT)
文档属性
| 名称 | 2023年高考数学客观题专题十一 圆锥曲线 课件(共52张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 12:27:54 | ||
图片预览








文档简介
(共52张PPT)
专题十一 圆锥曲线
【考试内容】 椭圆及其标准方程;椭圆的简单几何性质;双曲线及其标准方程;双曲线的简单几何性质;抛物线及其标准方程;抛物线的简单几何性质
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 5 10 10 10 5 10 10
全国卷(乙卷) 5 10 5 10 10 10 10
新高考全国Ⅰ卷 10 10
新高考全国Ⅱ卷 10 10
重要考点回顾
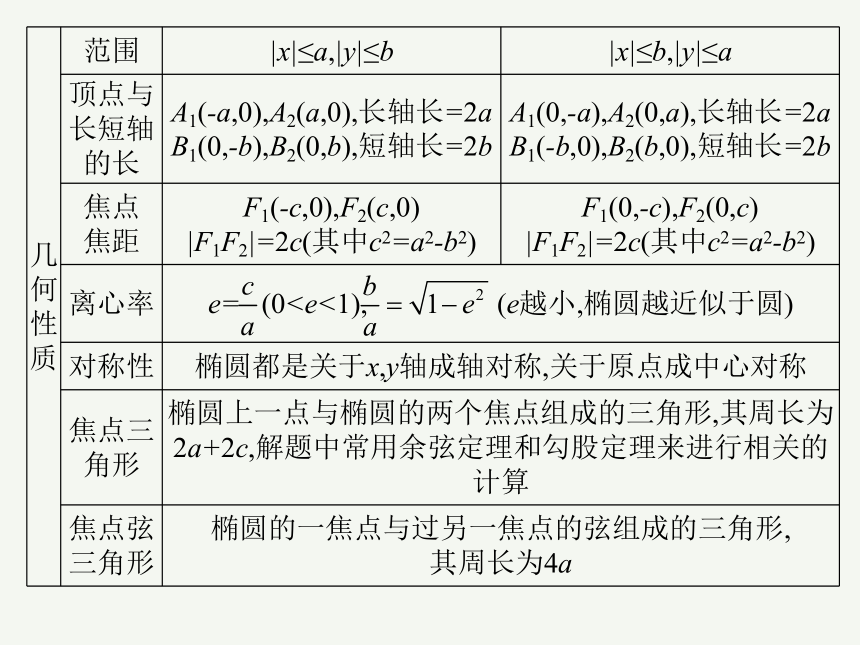
一、椭圆知识点
内容
定义 平面内与两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫椭圆.
图象
标准方程
几何性质 范围 |x|≤a,|y|≤b |x|≤b,|y|≤a
顶点与长短轴的长 A1(-a,0),A2(a,0),长轴长=2a B1(0,-b),B2(0,b),短轴长=2b A1(0,-a),A2(0,a),长轴长=2a
B1(-b,0),B2(b,0),短轴长=2b
焦点 焦距 F1(-c,0),F2(c,0) |F1F2|=2c(其中c2=a2-b2) F1(0,-c),F2(0,c)
|F1F2|=2c(其中c2=a2-b2)
离心率 e= (0对称性 椭圆都是关于x,y轴成轴对称,关于原点成中心对称
焦点三角形 椭圆上一点与椭圆的两个焦点组成的三角形,其周长为2a+2c,解题中常用余弦定理和勾股定理来进行相关的计算
焦点弦三角形 椭圆的一焦点与过另一焦点的弦组成的三角形, 其周长为4a
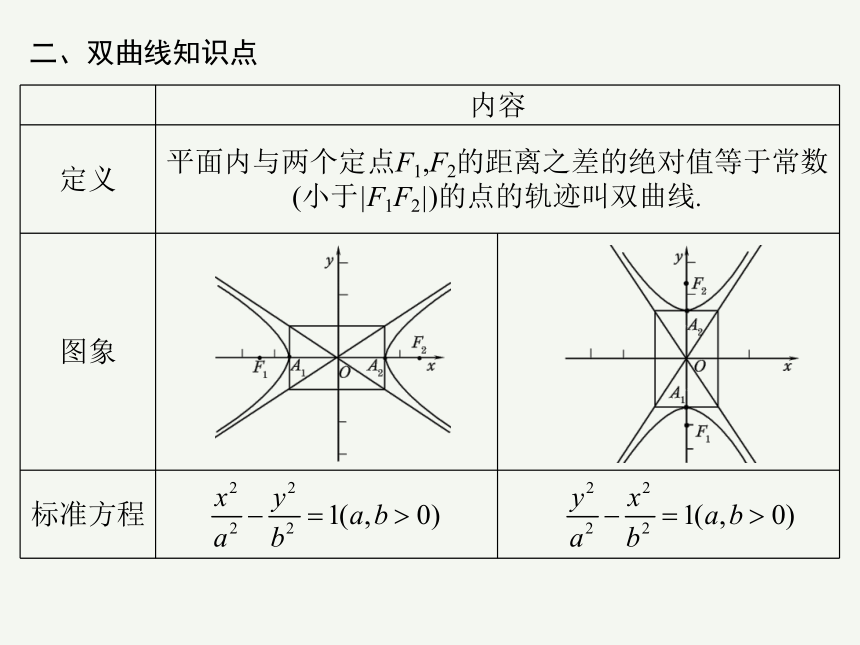
二、双曲线知识点
内容
定义 平面内与两个定点F1,F2的距离之差的绝对值等于常数(小于|F1F2|)的点的轨迹叫双曲线.
图象
标准方程
几何性质 范围 |x|≥a,y∈R x∈R,|y|≥a
顶点与实虚轴的长 A1(-a,0),A2(a,0),实轴长=2a 虚轴长=2b,a=b时叫等轴双曲线 A1(0,-a),A2(0,a),实轴长=2a
虚轴长=2b,a=b时叫等轴双曲线
焦点 焦距 F1(-c,0),F2(c,0) |F1F2|=2c(其中c2=a2+b2) F1(0,-c),F2(0,c)
|F1F2|=2c(其中c2=a2+b2)
渐近线方程
离心率 e= (e>1), (e越小,双曲线开口越小), 等轴双曲线的e=
对称性 双曲线都是关于x,y轴成轴对称,关于原点成中心对称
焦点三角形 双曲线上一点与双曲线的两个焦点组成的三角形,解题中常用余弦定理和勾股定理来进行相关的计算
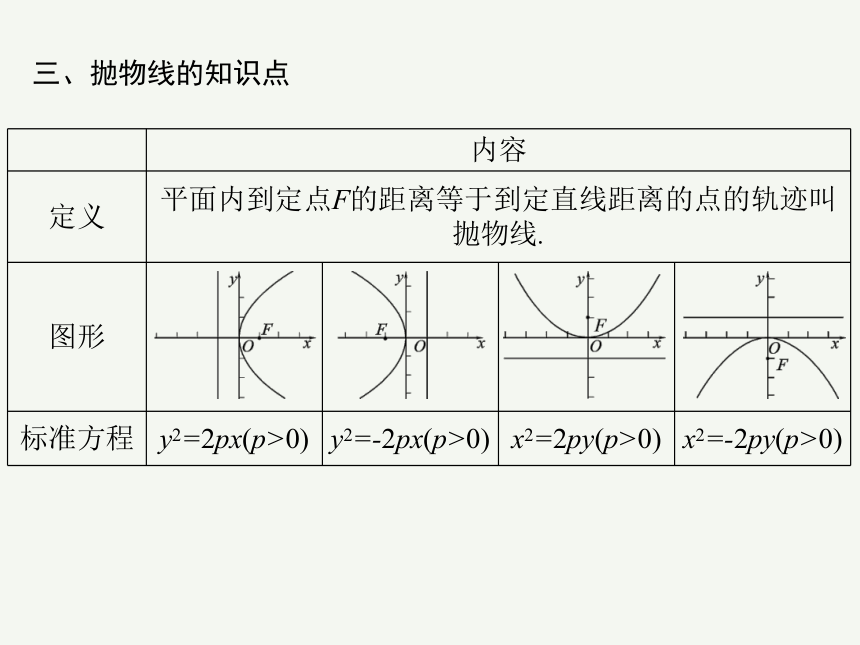
三、抛物线的知识点
内容
定义 平面内到定点F的距离等于到定直线距离的点的轨迹叫抛物线.
图形
标准方程 y2=2px(p>0) y2=-2px(p>0) x2=2py(p>0) x2=-2py(p>0)
几何性质 范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R
开口 方向 向右 向左 向上 向下
焦准距 p(p>0)
顶点 坐标 坐标原点(0,0)
焦点 坐标 F( ,0) F(- ,0) F(0, ) F(0,- )
准线 方程 l:x=- l:x= l:y=- l:y=
对称轴 x轴 x轴 y轴 y轴
离心率 e=1
考点训练
1.若一个椭圆长轴、短轴的长度和焦距成等差数列,则该椭圆的离心率是 ( )
A. B. C. D.
【答案】B
【解析】由题意可知2a+2c=2·2b,化简得a+c=2b,
两边平方得(a+c)2=4b2,(a+c)2=4(a2-c2),3a2-2ac-5c2=0,
即(a+c)(3a-5c)=0,
因为a+c≠0,于是有3a=5c,即e=.故选B.
2.已知椭圆的长轴长是短轴长的倍,则椭圆的离心率等于( )
A. B. C. D.
【答案】B
【解析】由已知得2a=·2b,即a2=2b2.
∵a2=b2+c2,得到c2=b2,
∴由e2===,解得e=.故选B.
3.若椭圆+y2=1的两个焦点为F1,F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则点P到F2的距离为 ( )
A. B. C. D.4
【答案】C
【解析】由椭圆的方程可知a2=4,b2=1,求得c2=3.
如图所示,可求得P点坐标为,|PF1|=.
根据椭圆的定义可知,|PF1|+|PF2|=2a=4,
解得|PF2|=4-|PF1|=4-=.故选C.
4.已知方程+=1(k∈R)表示焦点在x轴上的椭圆,则k的取值范围是 ( )
A.(-∞,1)(3,+∞) B.(1,3)
C.(1,+∞) D.(-∞,3)
【答案】B
【解析】由题意可知a2=k+1,b2=3-k,
则k+1>3-k>0,解得15.椭圆+=1(a>b>0)的左、右顶点分别是A,B,左、右焦点分别是F1,F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为( )
A. B. C. D.-2
【答案】B
【解析】由椭圆性质可知|AF1|=a-c,|F1F2|=2c,|F1B|=a+c.
因为三者成等比数列,所以(2c)2=(a-c)(a+c),
化简得5c2=a2,解得e=.故选B.
6.设F1,F2是椭圆E:+=1(a>b>0)的左、右焦点,P为直线x=上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
A. B. C. D.
【答案】C
【解析】如图,由题意可知|PF2|=|F1F2|=2c,|F2A|=-c.
因为∠F2F1P=∠F2PF1=30°,所以有∠PF2A=60°.
又PA⊥F2A,于是有∠F2PA=30°,故有|PF2|=2|AF2|,
即2c=2,化简得4c=3a,
于是e==.故选C.
7.已知双曲线-=1(a>0)的离心率为2,则a= ( )
A.2 B. C. D.1
【答案】D
【解析】由双曲线的离心率可得=2,解得a=1.故选D.
8.已知双曲线C:-=1(a>0,b>0)的离心率为,则C的渐近线方程为 ( )
A.y=±x B.y=±x C.y=±x D.y=±x
【答案】C
【解析】∵e=,∴=,即=.∵c2=a2+b2,∴=.∴=.
∴双曲线的渐近线方程为y=±x=±x.故选C.
9.已知双曲线的中心在坐标原点,离心率e=2,且它的一个顶点与抛物线y2=-8x的焦点重合,则此双曲线的方程为 ( )
A.x2-=1 B.-y2=1 C.-=1 D.-=1
【答案】D
【解析】因为抛物线y2=-8x的焦点为(-2,0),即双曲线的一个顶点为(-2,0),于是有a=2,
又e==2,所以c=4,从而有b==2.
故双曲线方程为-=1.故选D.
10.已知F1,F2为双曲线x2-y2=2的左、右焦点,点P在双曲线上,
|PF1|=2|PF2|,则cos∠F1PF2= ( )
A. B. C. D.
【答案】C
【解析】由双曲线x2-y2=2可得a=,b=,c=2.
由双曲线的定义可知,|PF1|-|PF2|=2|PF2|-|PF2|=|PF2|=2a=2,
于是有|PF1|=2|PF2|=4,又|F1F2|=2c=4,
由余弦定理可得cos∠F1PF2===.
故选C.
11.已知双曲线C:-=1的焦距为10,点P(2,1)在C的渐近线上,则C的方程为 ( )
A.-=1 B.-=1 C.-=1 D.-=1
【答案】A
【解析】双曲线C的其中一条渐近线方程为y=x,
点P(2,1)在该条直线上,可得=,
由题意可知2c=10且a2+b2=c2,解得b2=5,a2=20.故选A.
12.已知双曲线C1:-=1(a>0,b>0)与双曲线C2:-=1有相同的渐近线,且C1的右焦点为F(,0),则a= ,b= .
【答案】1;2
【解析】由双曲线C2的渐近线方程为y=±2x,
可知双曲线C1中=2,
且由题意可知c=,
∵a2+b2=c2,∴a2=1,b2=4.
解得a=1,b=2.
13.如图,F1,F2是双曲线C:-=1(a>0,b>0)的左、右焦点,过F1的直线l与C的左、右两支分别交于A,B两点.若|AB|∶|BF2|∶|AF2|
=3∶4∶5,则双曲线的离心率为 .
【答案】
【解析】由题意,可设|AB|=3t,|BF2|=4t,|AF2|=5t.
根据双曲线的定义可知,
|AF2|-|AF1|=2a,|BF1|-|BF2|=|BA|+|AF1|-|BF2|=2a.
两式相减得|AF1|=3t,2a=2t,a=t.
∵|AB|∶|BF2|∶|AF2|=3∶4∶5,
∴∠F1BF2=90°,有|BF1|2+|BF2|2=|F1F2|2,得到|F1F2|=2t.
于是2c=2t,得c=t.故e===.
14.已知双曲线的一个焦点与抛物线x2=24y的焦点重合,其中一条渐近线的倾斜角为60°,则该双曲线的标准方程为 ( )
A.-=1 B.-=1 C.-=1 D.-=1
【答案】B
【解析】抛物线x2=24y的焦点为(0,6),即双曲线的焦点为(0,±6),设双曲线的方程为-=1 (a>0,b>0),则c=6.
由渐近线方程为=tan 60°=,c2=b2+a2, 解得a=3,b=3,
则双曲线的方程为-=1.故选B.
15.O为坐标原点,F为抛物线C:y2=4x的焦点,P为C上一点,若|PF|=4,则△POF的面积为 ( )
A.2 B.2 C.2 D.4
【答案】C
【解析】由|PF|=4,可得P点到准线的距离也为4,
则P点横坐标为3.=4×3=24,
则P到x轴的距离为2.故S△POF=·|OF|·2=2.故选C.
16.设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,则|AB|= ( )
A. B.6 C.12 D.7
【答案】C
【解析】依题可得F,则直线AB方程为y=.
与抛物线方程联立可得x2-x+=0,则xA+xB=.
根据抛物线上点到焦点的距离和到准线的距离相等,且抛物线开口向右,则xA>0,xB>0,
可得|AB|=|AF|+|BF|=xA+xB+2×=12.故选C.
17.过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点,若|AF|=3,则|BF|= .
【答案】
【解析】由y2=4x知焦点F的坐标为(1,0),
若过点F的直线的斜率不存在,那么直线方程为x=1,此时直线与抛物线的两个交点为(1,2)和(1,-2),则|AF|=2,不合题意,故舍去.
设过焦点F的直线的斜率为k,那么直线的方程为y=k(x-1),
代入y2=4x中,得k2x2-(2k2+4)x+k2=0,
设A(x1,y1),B(x2,y2),那么x1x2=1.
而|AF|=x1+1=3,那么x1=2,所以x2=.所以|BF|=x2+1=.
18.若抛物线y2=2px的焦点与椭圆+=1的右焦点重合,则p的值为 ( )
A.-2 B.2 C.-4 D.4
【答案】D
【解析】椭圆方程为+=1,则a2=6,b2=2,c2=4,
椭圆右焦点为(2,0),
所以根据题意有=2,得p=4.故选D.
19.已知抛物线关于x轴对称,它的顶点在坐标原点O,并且经过点M(2,y0).若点M到该抛物线焦点的距离为3,则|OM|= ( )
A.2 B.2 C.4 D.2
【答案】B
【解析】由题意,抛物线关于x轴对称,开口向右,
设方程为y2=2px(p>0).
∵点M(2,y0)到该抛物线焦点的距离为3,
∴2+=3,∴p=2,∴抛物线方程为y2=4x.
∵M(2,y0),∴=8,
∴|OM|==2.故选B.
20.等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A,B两点,且|AB|=4,则C的实轴长为 ( )
A. B.2 C.4 D.8
【答案】C
【解析】设等轴双曲线C的方程为x2-y2=k ①,
抛物线y2=16x,2p=16,p=8,=4,准线方程为x=-=-4.
等轴双曲线与抛物线的准线x=-4的两个交点分别为A(-4,y),B(-4,-y),
则|AB|=|y-(-y)|=2y=4,y=2.
将x=-4,y=2代入①,化简得(-4)2-(2)2=k,k=4,a2=4,a=2,
所以C的实轴长为4.故选C.
21.已知椭圆E的中心为坐标原点,离心率为,E的右焦点与抛物线C:y2=8x的焦点重合,A,B是C的准线与E的两个交点,则|AB|=( )
A.3 B.6 C.9 D.12
【答案】B
【解析】∵抛物线C:y2=8x的焦点为(2,0),准线方程为x=-2,
∴椭圆E的右焦点为(2,0).∴椭圆E的焦点在x轴上,
设椭圆E方程为+=1(a>b>0),c=2,∵e==,∴a=4,b2=a2-c2=12.
∴椭圆E方程为+=1,
将x=-2代入椭圆E的方程解得A(-2,3),B(-2,-3),∴|AB|=6.故选B.
22.已知F是双曲线C:x2-=1的右焦点,P是C左支上一点,A(0,6),当△APF周长最小时,该三角形的面积为 .
【答案】12
【解析】设双曲线的左焦点为F1,由双曲线定义知,|PF|=2a+|PF1|,
∴△APF的周长为|PA|+|PF|+|AF|=|PA|+2a+|PF1|+|AF|=|PA|+|PF1|+|AF|+2a,
由于2a+|AF|是定值,要使△APF的周长最小,
则|PA|+|PF1|最小,即P,A,F1共线.
∵点A(0,6),F1(-3,0),
∴直线AF1的方程为+=1,即x=-3,代入x2-=1,
整理得y2+6y-96=0,解得y=2或y=-8(舍),
∴P点的纵坐标为2.
∴S△APF=-=×6×6-×6×2=12.
23.直线l经过椭圆的一个顶点和一个焦点,若椭圆中心到l的距离为其短轴长的,则该椭圆的离心率为 ( )
A. B. C. D.
【答案】B
【解析】如图,利用三角形等面积法得a·b=b·c,
则e==.故选B.
24.设F为抛物线C:y2=4x的焦点,曲线y=(k>0)与C交于点P,PF⊥x轴,则k= ( )
A. B.1 C. D.2
【答案】D
【解析】∵F为抛物线y2=4x的焦点,∴F(1,0).
又∵曲线y=(k>0)与C交于点P,PF⊥x轴,
∴P(1,2),∴=2,∴k=2.
故选D.
25.已知O为坐标原点,F是椭圆C:+=1(a>b>0)的左焦点,A,B分别为C的左、右顶点.P为C上一点,且PF⊥x轴.过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为 ( )
A. B. C. D.
【答案】A
【解析】由题意可设直线l的方程为y=k(x+a),
分别令x=-c与x=0得|FM|=k(a-c),|OE|=ka,
设OE中点为D,由△BMF∽△BDO,得=,即=,
整理得=,所以椭圆离心率为e=.故选A.
26.已知A为抛物线C:y2=2px(p>0)上一点,点A到C的焦点的距离为12,到y轴的距离为9,则p= ( )
A.2 B.3 C.6 D.9
【答案】C
【解析】因为抛物线上的点到焦点的距离和到准线的距离相等,
所以有9+=12,解得p=6.
故选C.
27.已知双曲线-=1(a>0,b>0)的右焦点与抛物线y2=2px(p>0)的焦点重合,抛物线的准线交双曲线于A,B两点,交双曲线的渐近线于C,D两点,若|CD|=|AB|,则双曲线的离心率为 ( )
A. B. C.2 D.3
【答案】A
【解析】由题意可得抛物线的准线方程为x=-.
设AB,CD与x轴分别交于点M,N,由|CD|=|AB|,
再由双曲线渐近线及抛物线的对称性可得|CN|=|AM|.
由题意可得=c,即p=2c,可得解得|y|=,所以|AM|=.
由可得|y|=,所以|CN|=.所以可得=·,可得c=b,
所以c2=2b2=2(c2-a2),解得c=a,
所以双曲线的离心率e==.故选A.
28.设双曲线C的方程为-=1(a>0,b>0),过抛物线y2=4x的焦点和点(0,b)的直线为l.若C的一条渐近线与l平行,另一条渐近线与l垂直,则双曲线C的方程为 ( )
A.-=1 B.x2-=1
C.-y2=1 D.x2-y2=1
【答案】D
【解析】抛物线y2=4x的焦点坐标为(1,0),
则直线l的方程为y=-b(x-1).
∵双曲线C:-=1(a>0,b>0)的渐近线方程为y=±x,
且C的一条渐近线与l平行,另一条渐近线与l垂直,
∴-=-b,·(-b)=-1.
∴a=1,b=1.
∴双曲线C的方程为x2-y2=1.故选D.
29.(多选题)已知双曲线C:-=1(a>0,b>0)的离心率e=2,C上的点到其焦点的最短距离为1,则 ( )
A.C的焦点坐标为(0,±2)
B.C的渐近线方程为y=±x
C.点(2,3)在C上
D.直线mx-y-m=0(m∈R)与C恒有两个交点
【答案】BC
【解析】由已知得所以所以b2=3,
所以双曲线C的方程为x2-=1.所以C的焦点为(±2,0),故A错误;
C的渐近线方程为y=±x=±x,故B正确;
因为22-=1,所以点(2,3)在C上,故C正确;
直线mx-y-m=0即y=m(x-1),恒过点(1,0),
当m=±时,直线与双曲线C的一条渐近线平行,此时直线与双曲线只有一个交点,故D错误.
故选BC.
30.(多选题)已知F1,F2是椭圆C:+=1(a>b>0)的左、右焦点,M,N是左、右顶点,e为椭圆C的离心率.过右焦点F2的直线l与椭圆交于A,B两点,已知·=0,3=2,|AF1|=2|AF2|.设直线AB的斜率为k,直线AM和直线AN的斜率分别为k1,k2,直线BM和直线BN的斜率分别为k3,k4,则下列结论一定正确的是 ( )
A.e= B.k=
C.k1·k2=- D.k3·k4=
【答案】AC
【解析】∵·=0,∴AF1⊥BF1.
过点F2作F1B的平行线,交AF1于点E,∴AF1⊥EF2.
设|F2A|=2t,|F1A|=4t,又3=2,∴|AB|=5t.
∵AF1⊥BF1,∴|F1B|=3t,∴12t=4a,∴a=3t.
∴|BF1|=|BF2|=3t=a,∴B(0,b),
在△EF1F2中,EF1=AF1=,EF2=BF1=,F1F2=2c,
∵E+E=F1,∴c=,b==,
∴椭圆离心率e==,故A正确;
【解析】k==2,故B错误;
设点A(x,y),易得点M(-a,0),N(a,0),
则k1·k2=·===-=-,故C正确;
同理k3·k4=-=-,故D错误.
故选AC.
31.(多选题)双曲线x2-=1(b>0)一条渐近线方程为2x+y=0,双曲线的离心率为e,双曲线的焦点到渐近线的距离为d,则 ( )
A.d=2 B.d= C.e=3 D.e=
【答案】AC
【解析】双曲线x2-=1(b>0)的一条渐近线方程为2x+y=0,
可得b=2,a=1,所以e===3,故C正确;
双曲线的右焦点(3,0),
双曲线的焦点到渐近线的距离为d==2,故A正确.
故选AC.
32.(多选题)已知抛物线x2=y的焦点为F,M(x1,y1),N(x2,y2)是抛物线上两点,则下列结论正确的是 ( )
A.点F的坐标为
B.若直线MN过点F,则x1x2=-
C.若=λ,则|MN|的最小值为
D.若|MF|+|NF|=,则线段MN的中点P到x轴的距离为
【答案】BCD
【解析】抛物线x2=y的焦点为F,故A错误;
根据抛物线的性质可得,MN过点F时,则x1x2=-,故B正确;
若=λ,则|MN|的最小值为抛物线的通径长,为2p=,故C正确;
【解析】抛物线x2=y的焦点为F,准线方程为y=-,
过点M,N,P分别作准线的垂线MM',NN',PP',
则|MM'|=|MF|,|NN'|=|NF|,|MM'|+|NN'|=|MF|+|NF|=,
所以|PP'|==,
所以线段MN中的P到x轴的距离为|PP'|-=-=,故D正确.
故选BCD.
33.(多选题)已知P是椭圆+=1上一动点,M,N分别是圆(x+2)2+y2=与圆(x-2)2+y2=一动点,则 ( )
A.|PM|+|PN|的最小值为
B.|PM|+|PN|的最小值为
C.|PM|+|PN|的最大值为
D.|PM|+|PN|的最大值为
【答案】AD
【解析】圆(x+2)2+y2=与圆(x-2)2+y2=的圆心分别为A(-2,0),
B(2,0),
则A,B是椭圆+=1的两个焦点坐标,两个圆的半径均为,
所以|PM|+|PN|的最大值为|PA|+|PB|+2×=2a+=2×+=;
|PM|+|PN|的最小值为|PA|+|PB|-2×=2a+=2×-=.
故选AD.
34.(多选题)双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1,F2,过F1的直线与双曲线C的左、右两支分别交于点M,N,若=,|F2M|=|MN|,则 ( )
A.|F1M|=a B.|F2N|=2a
C.cos∠F1NF2= D.离心率为2
【答案】ABC
【解析】如图,设F1M=m,
因为|F2M|=|MN|,根据双曲线定义可得|F2M|=|MN|=2a+m,
∴|F1N|=2a+2m,|F2N|=2m.
∵=,∴m=(2m+2a),∴m=a.
∴|F1M|=a,|F2N|=2a,故A,B正确;
在△MNF2中,|F2M|=|MN|=3a,|F2N|=2a,
即可得cos∠MNF2==,故C正确;
在三角形F1NF2中,
由|F2F1|2=|F1N|2+|F2N|2-2|F1N||F2N|cos∠MNF2,可得3c2=11a2,
故D错误.故选ABC.
35.(多选题)已知曲线C:mx2+ny2=1. ( )
A.若m>n>0,则C是椭圆,其焦点在y轴上
B.若m=n>0,则C是圆,其半径为
C.若mn<0,则C是双曲线,其渐近线方程为y=±x
D.若m=0,n>0,则C是两条直线
【答案】ACD
【解析】对于A,若m>n>0,则<,则根据椭圆定义,知+=1表示焦点在y轴上的椭圆,故A正确;
对于B,若m=n>0,则方程为x2+y2=,表示半径为的圆,故B错误;
对于C,若m<0,n>0,则方程为+=1,表示焦点在y轴的双曲线,
故此时渐近线方程为y=±x,
若m>0,n<0,则方程为+=1,表示焦点在x轴的双曲线,
故此时渐近线方程为y=±x,故C正确;
对于D,当m=0,n>0时,则方程为y=±,表示两条直线,故D正确.
故选ACD.
专题十一 圆锥曲线
【考试内容】 椭圆及其标准方程;椭圆的简单几何性质;双曲线及其标准方程;双曲线的简单几何性质;抛物线及其标准方程;抛物线的简单几何性质
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 5 10 10 10 5 10 10
全国卷(乙卷) 5 10 5 10 10 10 10
新高考全国Ⅰ卷 10 10
新高考全国Ⅱ卷 10 10
重要考点回顾
一、椭圆知识点
内容
定义 平面内与两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫椭圆.
图象
标准方程
几何性质 范围 |x|≤a,|y|≤b |x|≤b,|y|≤a
顶点与长短轴的长 A1(-a,0),A2(a,0),长轴长=2a B1(0,-b),B2(0,b),短轴长=2b A1(0,-a),A2(0,a),长轴长=2a
B1(-b,0),B2(b,0),短轴长=2b
焦点 焦距 F1(-c,0),F2(c,0) |F1F2|=2c(其中c2=a2-b2) F1(0,-c),F2(0,c)
|F1F2|=2c(其中c2=a2-b2)
离心率 e= (0
焦点三角形 椭圆上一点与椭圆的两个焦点组成的三角形,其周长为2a+2c,解题中常用余弦定理和勾股定理来进行相关的计算
焦点弦三角形 椭圆的一焦点与过另一焦点的弦组成的三角形, 其周长为4a
二、双曲线知识点
内容
定义 平面内与两个定点F1,F2的距离之差的绝对值等于常数(小于|F1F2|)的点的轨迹叫双曲线.
图象
标准方程
几何性质 范围 |x|≥a,y∈R x∈R,|y|≥a
顶点与实虚轴的长 A1(-a,0),A2(a,0),实轴长=2a 虚轴长=2b,a=b时叫等轴双曲线 A1(0,-a),A2(0,a),实轴长=2a
虚轴长=2b,a=b时叫等轴双曲线
焦点 焦距 F1(-c,0),F2(c,0) |F1F2|=2c(其中c2=a2+b2) F1(0,-c),F2(0,c)
|F1F2|=2c(其中c2=a2+b2)
渐近线方程
离心率 e= (e>1), (e越小,双曲线开口越小), 等轴双曲线的e=
对称性 双曲线都是关于x,y轴成轴对称,关于原点成中心对称
焦点三角形 双曲线上一点与双曲线的两个焦点组成的三角形,解题中常用余弦定理和勾股定理来进行相关的计算
三、抛物线的知识点
内容
定义 平面内到定点F的距离等于到定直线距离的点的轨迹叫抛物线.
图形
标准方程 y2=2px(p>0) y2=-2px(p>0) x2=2py(p>0) x2=-2py(p>0)
几何性质 范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R
开口 方向 向右 向左 向上 向下
焦准距 p(p>0)
顶点 坐标 坐标原点(0,0)
焦点 坐标 F( ,0) F(- ,0) F(0, ) F(0,- )
准线 方程 l:x=- l:x= l:y=- l:y=
对称轴 x轴 x轴 y轴 y轴
离心率 e=1
考点训练
1.若一个椭圆长轴、短轴的长度和焦距成等差数列,则该椭圆的离心率是 ( )
A. B. C. D.
【答案】B
【解析】由题意可知2a+2c=2·2b,化简得a+c=2b,
两边平方得(a+c)2=4b2,(a+c)2=4(a2-c2),3a2-2ac-5c2=0,
即(a+c)(3a-5c)=0,
因为a+c≠0,于是有3a=5c,即e=.故选B.
2.已知椭圆的长轴长是短轴长的倍,则椭圆的离心率等于( )
A. B. C. D.
【答案】B
【解析】由已知得2a=·2b,即a2=2b2.
∵a2=b2+c2,得到c2=b2,
∴由e2===,解得e=.故选B.
3.若椭圆+y2=1的两个焦点为F1,F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则点P到F2的距离为 ( )
A. B. C. D.4
【答案】C
【解析】由椭圆的方程可知a2=4,b2=1,求得c2=3.
如图所示,可求得P点坐标为,|PF1|=.
根据椭圆的定义可知,|PF1|+|PF2|=2a=4,
解得|PF2|=4-|PF1|=4-=.故选C.
4.已知方程+=1(k∈R)表示焦点在x轴上的椭圆,则k的取值范围是 ( )
A.(-∞,1)(3,+∞) B.(1,3)
C.(1,+∞) D.(-∞,3)
【答案】B
【解析】由题意可知a2=k+1,b2=3-k,
则k+1>3-k>0,解得1
A. B. C. D.-2
【答案】B
【解析】由椭圆性质可知|AF1|=a-c,|F1F2|=2c,|F1B|=a+c.
因为三者成等比数列,所以(2c)2=(a-c)(a+c),
化简得5c2=a2,解得e=.故选B.
6.设F1,F2是椭圆E:+=1(a>b>0)的左、右焦点,P为直线x=上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
A. B. C. D.
【答案】C
【解析】如图,由题意可知|PF2|=|F1F2|=2c,|F2A|=-c.
因为∠F2F1P=∠F2PF1=30°,所以有∠PF2A=60°.
又PA⊥F2A,于是有∠F2PA=30°,故有|PF2|=2|AF2|,
即2c=2,化简得4c=3a,
于是e==.故选C.
7.已知双曲线-=1(a>0)的离心率为2,则a= ( )
A.2 B. C. D.1
【答案】D
【解析】由双曲线的离心率可得=2,解得a=1.故选D.
8.已知双曲线C:-=1(a>0,b>0)的离心率为,则C的渐近线方程为 ( )
A.y=±x B.y=±x C.y=±x D.y=±x
【答案】C
【解析】∵e=,∴=,即=.∵c2=a2+b2,∴=.∴=.
∴双曲线的渐近线方程为y=±x=±x.故选C.
9.已知双曲线的中心在坐标原点,离心率e=2,且它的一个顶点与抛物线y2=-8x的焦点重合,则此双曲线的方程为 ( )
A.x2-=1 B.-y2=1 C.-=1 D.-=1
【答案】D
【解析】因为抛物线y2=-8x的焦点为(-2,0),即双曲线的一个顶点为(-2,0),于是有a=2,
又e==2,所以c=4,从而有b==2.
故双曲线方程为-=1.故选D.
10.已知F1,F2为双曲线x2-y2=2的左、右焦点,点P在双曲线上,
|PF1|=2|PF2|,则cos∠F1PF2= ( )
A. B. C. D.
【答案】C
【解析】由双曲线x2-y2=2可得a=,b=,c=2.
由双曲线的定义可知,|PF1|-|PF2|=2|PF2|-|PF2|=|PF2|=2a=2,
于是有|PF1|=2|PF2|=4,又|F1F2|=2c=4,
由余弦定理可得cos∠F1PF2===.
故选C.
11.已知双曲线C:-=1的焦距为10,点P(2,1)在C的渐近线上,则C的方程为 ( )
A.-=1 B.-=1 C.-=1 D.-=1
【答案】A
【解析】双曲线C的其中一条渐近线方程为y=x,
点P(2,1)在该条直线上,可得=,
由题意可知2c=10且a2+b2=c2,解得b2=5,a2=20.故选A.
12.已知双曲线C1:-=1(a>0,b>0)与双曲线C2:-=1有相同的渐近线,且C1的右焦点为F(,0),则a= ,b= .
【答案】1;2
【解析】由双曲线C2的渐近线方程为y=±2x,
可知双曲线C1中=2,
且由题意可知c=,
∵a2+b2=c2,∴a2=1,b2=4.
解得a=1,b=2.
13.如图,F1,F2是双曲线C:-=1(a>0,b>0)的左、右焦点,过F1的直线l与C的左、右两支分别交于A,B两点.若|AB|∶|BF2|∶|AF2|
=3∶4∶5,则双曲线的离心率为 .
【答案】
【解析】由题意,可设|AB|=3t,|BF2|=4t,|AF2|=5t.
根据双曲线的定义可知,
|AF2|-|AF1|=2a,|BF1|-|BF2|=|BA|+|AF1|-|BF2|=2a.
两式相减得|AF1|=3t,2a=2t,a=t.
∵|AB|∶|BF2|∶|AF2|=3∶4∶5,
∴∠F1BF2=90°,有|BF1|2+|BF2|2=|F1F2|2,得到|F1F2|=2t.
于是2c=2t,得c=t.故e===.
14.已知双曲线的一个焦点与抛物线x2=24y的焦点重合,其中一条渐近线的倾斜角为60°,则该双曲线的标准方程为 ( )
A.-=1 B.-=1 C.-=1 D.-=1
【答案】B
【解析】抛物线x2=24y的焦点为(0,6),即双曲线的焦点为(0,±6),设双曲线的方程为-=1 (a>0,b>0),则c=6.
由渐近线方程为=tan 60°=,c2=b2+a2, 解得a=3,b=3,
则双曲线的方程为-=1.故选B.
15.O为坐标原点,F为抛物线C:y2=4x的焦点,P为C上一点,若|PF|=4,则△POF的面积为 ( )
A.2 B.2 C.2 D.4
【答案】C
【解析】由|PF|=4,可得P点到准线的距离也为4,
则P点横坐标为3.=4×3=24,
则P到x轴的距离为2.故S△POF=·|OF|·2=2.故选C.
16.设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,则|AB|= ( )
A. B.6 C.12 D.7
【答案】C
【解析】依题可得F,则直线AB方程为y=.
与抛物线方程联立可得x2-x+=0,则xA+xB=.
根据抛物线上点到焦点的距离和到准线的距离相等,且抛物线开口向右,则xA>0,xB>0,
可得|AB|=|AF|+|BF|=xA+xB+2×=12.故选C.
17.过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点,若|AF|=3,则|BF|= .
【答案】
【解析】由y2=4x知焦点F的坐标为(1,0),
若过点F的直线的斜率不存在,那么直线方程为x=1,此时直线与抛物线的两个交点为(1,2)和(1,-2),则|AF|=2,不合题意,故舍去.
设过焦点F的直线的斜率为k,那么直线的方程为y=k(x-1),
代入y2=4x中,得k2x2-(2k2+4)x+k2=0,
设A(x1,y1),B(x2,y2),那么x1x2=1.
而|AF|=x1+1=3,那么x1=2,所以x2=.所以|BF|=x2+1=.
18.若抛物线y2=2px的焦点与椭圆+=1的右焦点重合,则p的值为 ( )
A.-2 B.2 C.-4 D.4
【答案】D
【解析】椭圆方程为+=1,则a2=6,b2=2,c2=4,
椭圆右焦点为(2,0),
所以根据题意有=2,得p=4.故选D.
19.已知抛物线关于x轴对称,它的顶点在坐标原点O,并且经过点M(2,y0).若点M到该抛物线焦点的距离为3,则|OM|= ( )
A.2 B.2 C.4 D.2
【答案】B
【解析】由题意,抛物线关于x轴对称,开口向右,
设方程为y2=2px(p>0).
∵点M(2,y0)到该抛物线焦点的距离为3,
∴2+=3,∴p=2,∴抛物线方程为y2=4x.
∵M(2,y0),∴=8,
∴|OM|==2.故选B.
20.等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A,B两点,且|AB|=4,则C的实轴长为 ( )
A. B.2 C.4 D.8
【答案】C
【解析】设等轴双曲线C的方程为x2-y2=k ①,
抛物线y2=16x,2p=16,p=8,=4,准线方程为x=-=-4.
等轴双曲线与抛物线的准线x=-4的两个交点分别为A(-4,y),B(-4,-y),
则|AB|=|y-(-y)|=2y=4,y=2.
将x=-4,y=2代入①,化简得(-4)2-(2)2=k,k=4,a2=4,a=2,
所以C的实轴长为4.故选C.
21.已知椭圆E的中心为坐标原点,离心率为,E的右焦点与抛物线C:y2=8x的焦点重合,A,B是C的准线与E的两个交点,则|AB|=( )
A.3 B.6 C.9 D.12
【答案】B
【解析】∵抛物线C:y2=8x的焦点为(2,0),准线方程为x=-2,
∴椭圆E的右焦点为(2,0).∴椭圆E的焦点在x轴上,
设椭圆E方程为+=1(a>b>0),c=2,∵e==,∴a=4,b2=a2-c2=12.
∴椭圆E方程为+=1,
将x=-2代入椭圆E的方程解得A(-2,3),B(-2,-3),∴|AB|=6.故选B.
22.已知F是双曲线C:x2-=1的右焦点,P是C左支上一点,A(0,6),当△APF周长最小时,该三角形的面积为 .
【答案】12
【解析】设双曲线的左焦点为F1,由双曲线定义知,|PF|=2a+|PF1|,
∴△APF的周长为|PA|+|PF|+|AF|=|PA|+2a+|PF1|+|AF|=|PA|+|PF1|+|AF|+2a,
由于2a+|AF|是定值,要使△APF的周长最小,
则|PA|+|PF1|最小,即P,A,F1共线.
∵点A(0,6),F1(-3,0),
∴直线AF1的方程为+=1,即x=-3,代入x2-=1,
整理得y2+6y-96=0,解得y=2或y=-8(舍),
∴P点的纵坐标为2.
∴S△APF=-=×6×6-×6×2=12.
23.直线l经过椭圆的一个顶点和一个焦点,若椭圆中心到l的距离为其短轴长的,则该椭圆的离心率为 ( )
A. B. C. D.
【答案】B
【解析】如图,利用三角形等面积法得a·b=b·c,
则e==.故选B.
24.设F为抛物线C:y2=4x的焦点,曲线y=(k>0)与C交于点P,PF⊥x轴,则k= ( )
A. B.1 C. D.2
【答案】D
【解析】∵F为抛物线y2=4x的焦点,∴F(1,0).
又∵曲线y=(k>0)与C交于点P,PF⊥x轴,
∴P(1,2),∴=2,∴k=2.
故选D.
25.已知O为坐标原点,F是椭圆C:+=1(a>b>0)的左焦点,A,B分别为C的左、右顶点.P为C上一点,且PF⊥x轴.过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为 ( )
A. B. C. D.
【答案】A
【解析】由题意可设直线l的方程为y=k(x+a),
分别令x=-c与x=0得|FM|=k(a-c),|OE|=ka,
设OE中点为D,由△BMF∽△BDO,得=,即=,
整理得=,所以椭圆离心率为e=.故选A.
26.已知A为抛物线C:y2=2px(p>0)上一点,点A到C的焦点的距离为12,到y轴的距离为9,则p= ( )
A.2 B.3 C.6 D.9
【答案】C
【解析】因为抛物线上的点到焦点的距离和到准线的距离相等,
所以有9+=12,解得p=6.
故选C.
27.已知双曲线-=1(a>0,b>0)的右焦点与抛物线y2=2px(p>0)的焦点重合,抛物线的准线交双曲线于A,B两点,交双曲线的渐近线于C,D两点,若|CD|=|AB|,则双曲线的离心率为 ( )
A. B. C.2 D.3
【答案】A
【解析】由题意可得抛物线的准线方程为x=-.
设AB,CD与x轴分别交于点M,N,由|CD|=|AB|,
再由双曲线渐近线及抛物线的对称性可得|CN|=|AM|.
由题意可得=c,即p=2c,可得解得|y|=,所以|AM|=.
由可得|y|=,所以|CN|=.所以可得=·,可得c=b,
所以c2=2b2=2(c2-a2),解得c=a,
所以双曲线的离心率e==.故选A.
28.设双曲线C的方程为-=1(a>0,b>0),过抛物线y2=4x的焦点和点(0,b)的直线为l.若C的一条渐近线与l平行,另一条渐近线与l垂直,则双曲线C的方程为 ( )
A.-=1 B.x2-=1
C.-y2=1 D.x2-y2=1
【答案】D
【解析】抛物线y2=4x的焦点坐标为(1,0),
则直线l的方程为y=-b(x-1).
∵双曲线C:-=1(a>0,b>0)的渐近线方程为y=±x,
且C的一条渐近线与l平行,另一条渐近线与l垂直,
∴-=-b,·(-b)=-1.
∴a=1,b=1.
∴双曲线C的方程为x2-y2=1.故选D.
29.(多选题)已知双曲线C:-=1(a>0,b>0)的离心率e=2,C上的点到其焦点的最短距离为1,则 ( )
A.C的焦点坐标为(0,±2)
B.C的渐近线方程为y=±x
C.点(2,3)在C上
D.直线mx-y-m=0(m∈R)与C恒有两个交点
【答案】BC
【解析】由已知得所以所以b2=3,
所以双曲线C的方程为x2-=1.所以C的焦点为(±2,0),故A错误;
C的渐近线方程为y=±x=±x,故B正确;
因为22-=1,所以点(2,3)在C上,故C正确;
直线mx-y-m=0即y=m(x-1),恒过点(1,0),
当m=±时,直线与双曲线C的一条渐近线平行,此时直线与双曲线只有一个交点,故D错误.
故选BC.
30.(多选题)已知F1,F2是椭圆C:+=1(a>b>0)的左、右焦点,M,N是左、右顶点,e为椭圆C的离心率.过右焦点F2的直线l与椭圆交于A,B两点,已知·=0,3=2,|AF1|=2|AF2|.设直线AB的斜率为k,直线AM和直线AN的斜率分别为k1,k2,直线BM和直线BN的斜率分别为k3,k4,则下列结论一定正确的是 ( )
A.e= B.k=
C.k1·k2=- D.k3·k4=
【答案】AC
【解析】∵·=0,∴AF1⊥BF1.
过点F2作F1B的平行线,交AF1于点E,∴AF1⊥EF2.
设|F2A|=2t,|F1A|=4t,又3=2,∴|AB|=5t.
∵AF1⊥BF1,∴|F1B|=3t,∴12t=4a,∴a=3t.
∴|BF1|=|BF2|=3t=a,∴B(0,b),
在△EF1F2中,EF1=AF1=,EF2=BF1=,F1F2=2c,
∵E+E=F1,∴c=,b==,
∴椭圆离心率e==,故A正确;
【解析】k==2,故B错误;
设点A(x,y),易得点M(-a,0),N(a,0),
则k1·k2=·===-=-,故C正确;
同理k3·k4=-=-,故D错误.
故选AC.
31.(多选题)双曲线x2-=1(b>0)一条渐近线方程为2x+y=0,双曲线的离心率为e,双曲线的焦点到渐近线的距离为d,则 ( )
A.d=2 B.d= C.e=3 D.e=
【答案】AC
【解析】双曲线x2-=1(b>0)的一条渐近线方程为2x+y=0,
可得b=2,a=1,所以e===3,故C正确;
双曲线的右焦点(3,0),
双曲线的焦点到渐近线的距离为d==2,故A正确.
故选AC.
32.(多选题)已知抛物线x2=y的焦点为F,M(x1,y1),N(x2,y2)是抛物线上两点,则下列结论正确的是 ( )
A.点F的坐标为
B.若直线MN过点F,则x1x2=-
C.若=λ,则|MN|的最小值为
D.若|MF|+|NF|=,则线段MN的中点P到x轴的距离为
【答案】BCD
【解析】抛物线x2=y的焦点为F,故A错误;
根据抛物线的性质可得,MN过点F时,则x1x2=-,故B正确;
若=λ,则|MN|的最小值为抛物线的通径长,为2p=,故C正确;
【解析】抛物线x2=y的焦点为F,准线方程为y=-,
过点M,N,P分别作准线的垂线MM',NN',PP',
则|MM'|=|MF|,|NN'|=|NF|,|MM'|+|NN'|=|MF|+|NF|=,
所以|PP'|==,
所以线段MN中的P到x轴的距离为|PP'|-=-=,故D正确.
故选BCD.
33.(多选题)已知P是椭圆+=1上一动点,M,N分别是圆(x+2)2+y2=与圆(x-2)2+y2=一动点,则 ( )
A.|PM|+|PN|的最小值为
B.|PM|+|PN|的最小值为
C.|PM|+|PN|的最大值为
D.|PM|+|PN|的最大值为
【答案】AD
【解析】圆(x+2)2+y2=与圆(x-2)2+y2=的圆心分别为A(-2,0),
B(2,0),
则A,B是椭圆+=1的两个焦点坐标,两个圆的半径均为,
所以|PM|+|PN|的最大值为|PA|+|PB|+2×=2a+=2×+=;
|PM|+|PN|的最小值为|PA|+|PB|-2×=2a+=2×-=.
故选AD.
34.(多选题)双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1,F2,过F1的直线与双曲线C的左、右两支分别交于点M,N,若=,|F2M|=|MN|,则 ( )
A.|F1M|=a B.|F2N|=2a
C.cos∠F1NF2= D.离心率为2
【答案】ABC
【解析】如图,设F1M=m,
因为|F2M|=|MN|,根据双曲线定义可得|F2M|=|MN|=2a+m,
∴|F1N|=2a+2m,|F2N|=2m.
∵=,∴m=(2m+2a),∴m=a.
∴|F1M|=a,|F2N|=2a,故A,B正确;
在△MNF2中,|F2M|=|MN|=3a,|F2N|=2a,
即可得cos∠MNF2==,故C正确;
在三角形F1NF2中,
由|F2F1|2=|F1N|2+|F2N|2-2|F1N||F2N|cos∠MNF2,可得3c2=11a2,
故D错误.故选ABC.
35.(多选题)已知曲线C:mx2+ny2=1. ( )
A.若m>n>0,则C是椭圆,其焦点在y轴上
B.若m=n>0,则C是圆,其半径为
C.若mn<0,则C是双曲线,其渐近线方程为y=±x
D.若m=0,n>0,则C是两条直线
【答案】ACD
【解析】对于A,若m>n>0,则<,则根据椭圆定义,知+=1表示焦点在y轴上的椭圆,故A正确;
对于B,若m=n>0,则方程为x2+y2=,表示半径为的圆,故B错误;
对于C,若m<0,n>0,则方程为+=1,表示焦点在y轴的双曲线,
故此时渐近线方程为y=±x,
若m>0,n<0,则方程为+=1,表示焦点在x轴的双曲线,
故此时渐近线方程为y=±x,故C正确;
对于D,当m=0,n>0时,则方程为y=±,表示两条直线,故D正确.
故选ACD.
同课章节目录
