2023年高考数学客观题专题六 函数与导数 课件(共82张PPT)
文档属性
| 名称 | 2023年高考数学客观题专题六 函数与导数 课件(共82张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 12:29:19 | ||
图片预览










文档简介
(共82张PPT)
专题六 函数与导数
【考试内容】 函数及其表示;函数的图象;函数的性质;指数函数;对数函数;幂函数;函数的零点;导数的应用
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 10 10 15 10 10 15 10
全国卷(乙卷) 15 15 15 15 10 15 10
新高考全国Ⅰ卷 15 20
新高考全国Ⅱ卷 15 10
重要考点回顾
一、函数的基本性质
1.函数的单调性:
(1)f(x)在区间M上是增函数 x1,x2∈M,当x1(2)f(x)在区间M上是减函数 x1,x2∈M,当x1f(x2).
(记忆方法:不等号相同为增,不同为减,即同增异减)
2.函数的奇偶性:
(1)奇函数、偶函数的定义:
如果对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),则称函数y=f(x)是偶函数;
如果对于函数f(x)的定义域内的任意一个x,都有f(-x)=-f(x),则称函数y=f(x)是奇函数.
(2)奇、偶函数的性质:
①偶函数的图象关于y轴对称;奇函数的图象关于原点对称.
②奇函数f(x)的定义域中若含有0,则必有f(0)=0.
(3)常见的奇函数与偶函数:
①常见的奇函数:
正比例函数:f(x)=kx(x∈R);
反比例函数:f(x)=(x∈(-∞,0)∪(0,+∞));
正弦函数:f(x)=sin x(x∈R);
正切函数:f(x)=tan x
幂函数:f(x) =xn(x∈R)当n为奇数时f(x)=xn为奇函数.
几种特殊的奇函数:
②常见的偶函数:
余弦函数:f(x)=cosx(x∈R);
幂函数:f(x)=xn(x∈R)当n为偶数时f(x)=xn为偶函数.
几种特殊的偶函数:
f(x)=c(c为常数); f(x)=|x|;
f(x)= ; f(x)=|x+1|+|x-1|.
③在定义域符合要求的前提下:
奇函数与奇函数的和是奇函数;偶函数与偶函数的和是偶函数;
奇函数与奇函数的积是偶函数;偶函数与偶函数的积是偶函数;
奇函数与偶函数的积是奇函数;
奇函数与偶函数的和是非奇非偶函数;
如:f(x)=ax3+bx,f(x)=ax+ 是奇函数;
f(x)=ax2+c,f(x)= ax4+bx2+c,f(x)= ·x是偶函数;
f(x)=x2-x+1是非奇非偶函数.
3.函数的周期性:
(1)定义:对定义域内的任意x,若有f(x+T)=f(x)(其中T为非零常数),则称函数f(x)为周期函数,T为它的一个周期.所有正周期中最小的称为函数的最小正周期.如没有特别说明,文中所指的周期都指最小正周期.
(2)三角函数的最小正周期:
①y=sin x:T=2π; ②y=cos x:T=2π;
③y=tan x:T=π; ④y=Asin(ωx+φ),y=Acos(ωx+φ):T= ;
⑤y=tan ωx:T=
4.函数定义域的求法:列出使函数有意义的自变量的不等关系式,求解即可求得函数的定义域.常涉及的依据为:
①分母不为0;
②偶次根式中被开方数不小于0;
③对数的真数大于0,底数大于0且不等于1;
④零指数幂的底数不等于0;
⑤实际问题要考虑实际意义.
二、基本初等函数
指数、对数的运算性质:
(1)幂的运算性质:aman=am+n; (am)n=amn; (ab)m=ambm;
a0=1(a≠0);
(2)对数的概念:一般地,如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作:logaN
其中a叫做对数的底数,N叫做对数的真数.
以10为底的对数叫做常用对数;记作:lg.
以e为底的对数叫做自然对数;记作:ln.
(3)对数的简单性质:
①负数和零没有对数;
②底的对数是1,即logaa=1;
③1的对数是零,即loga1=0.
(4)对数的运算法则:如果a>0,且a≠1,M>0,N>0,那么:
①loga(MN)=logaM+logaN;
②loga( )=logaM-logaN;
③logaMn=nlogaM(n∈R);
④logab= (a>0,且a≠1,c>0,且c≠1,b>0)(对数换底公式);
⑤对数恒等式:
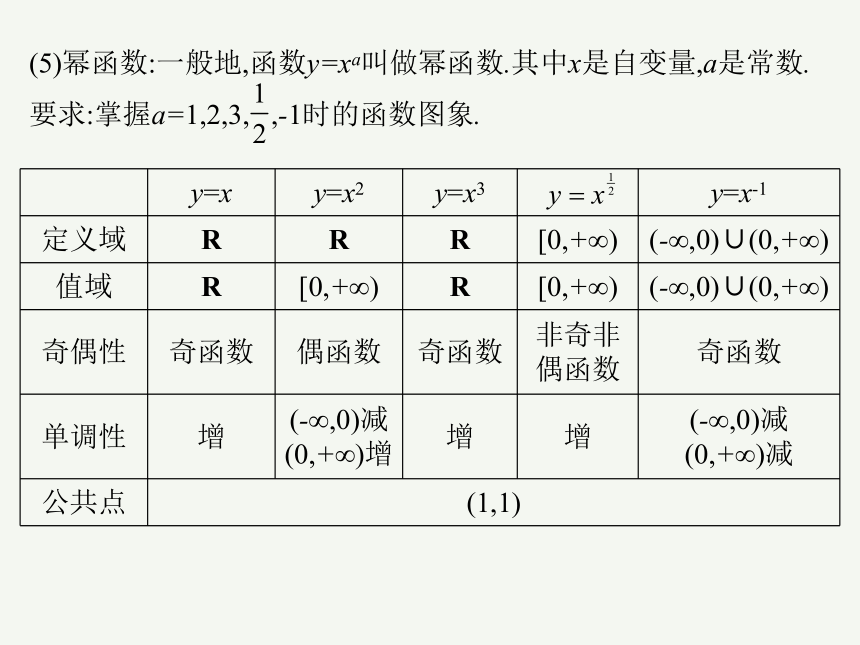
(5)幂函数:一般地,函数y=xa叫做幂函数.其中x是自变量,a是常数.
要求:掌握a=1,2,3, ,-1时的函数图象.
y=x y=x2 y=x3 y=x-1
定义域 R R R [0,+∞) (-∞,0)∪(0,+∞)
值域 R [0,+∞) R [0,+∞) (-∞,0)∪(0,+∞)
奇偶性 奇函数 偶函数 奇函数 非奇非偶函数 奇函数
单调性 增 (-∞,0)减 (0,+∞)增 增 增 (-∞,0)减
(0,+∞)减
公共点 (1,1)
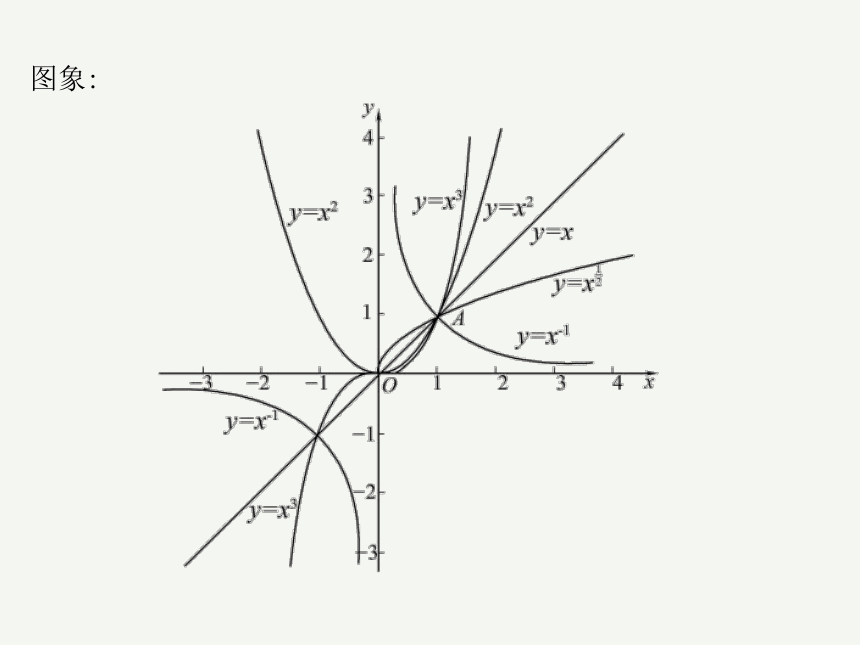
图象:
(6)指数函数:y=ax(a>0,a≠1)
图象恒过点(0,1),单调性与a的值有关,在解题中,往往要对a分a>1和0(7)对数函数:y=logax(a>0,a≠1)
图象恒过点(1,0),单调性与a的值有关,在解题中,往往要对a分a>1和0名称 指数函数 对数函数
一般形式 y=ax(a>0,a≠1) y=logax(a>0,a≠1)
定义域 R (0,+∞)
值域 (0,+∞) R
单调性 a>1 单调递增 a>1 单调递增
0特殊点 (0,1) (1,0)
图象
(8)注意的几个问题:
①y=ax与y=logax 的图象关系是关于直线y=x对称;这两个函数互为反函数.
②比较两个指数式或对数式的大小的基本方法是构造相应的指数或对数函数,若底数不相同时转化为同底数的指数或对数,还要注意与1或0比较.
三、导数
1.意义:函数f(x)在点P处的导数就是函数f(x)的图象在点P处的切线的斜率.
即:k=f'(x0)表示过曲线y=f(x)上的点P(x0,f(x0))的切线的斜率.
2.几种常见的函数导数:
①C'=0(C为常数) ⑤(ln x)'=
②(xn)'=nxn-1(n∈R) ⑥(logax)'=
③(sin x)'=cos x ⑦(ex)'=ex
④(cos x)'=-sin x ⑧(ax)'=axln a
3.求导数的四则运算法则:
[f(x)±g(x)]'=f'(x)±g'(x);
[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x);
4.导数的应用:
(1)求切线的斜率,以及求切线方程.
(2)利用导数判断函数的单调性:
若f'(x)>0,x∈(a,b)则f(x)在(a,b)上为增函数;
若f'(x)<0,x∈(a,b)则f(x)在(a,b)上为减函数.
(3)单调区间的求解过程,已知y=f(x)
①分析y=f(x)的定义域;
②求导数y'=f'(x);
③解不等式f'(x)>0,解集在定义域内的部分为增区间;
④解不等式f'(x)<0,解集在定义域内的部分为减区间.
(4)求极值、求最值.
①求函数y=f(x)的极值的方法:
先解方程f'(x)=0,当f'(x0)=0时:
(Ⅰ)如果在x0附近的左侧f'(x)>0,右侧f'(x)<0,那么f(x0)是极大值;
(Ⅱ)如果在x0附近的左侧f'(x)<0,右侧f'(x)>0,那么f(x0)是极小值.
②求函数y=f(x)在[a,b]上的最值的步骤:
(Ⅰ)求函数y=f(x)在(a,b)内的极值;
(Ⅱ)将函数y=f(x)的各极值与端点处的函数值f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
注意:
(1)若当x=x0时函数f(x)有极值,必有f'(x0)=0.但反之不成立;
(2)若函数f(x)在[a,b]上单调递增,则f(a)为函数的最小值,f(b)为函数的最大值;
函数f(x)在[a,b]上单调递减,则f(a)为函数的最大值,f(b)为函数的最小值.
四、函数的零点及二分法
1.对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)的图象与x轴的交点的横坐标.即:
方程f(x)=0有实数根 函数y=f(x)的图象与x轴有交点 函数y=f(x)有零点.
2.定理:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有:f(a)f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
3.二分法的定义:对于在区间[a,b]上连续不断且f(a)f(b)<0的函数y=f(x),通过不断地把函数f(x)所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
4.二分法的步骤:
(1)确定区间[a,b],验证f(a)f(b)<0,给定精确度ε;
(2)求区间的中点x1;
(3)计算f(x1):
①若f(x1)=0,则x1就是函数的零点;
②若f(a)f(x1)<0,则令b=x1(此时零点x0∈(a,x1));
③若f(a)f(x1)>0,则令a=x1(此时零点x0∈(x1,b)).
(4)判断是否达到精确度ε:即|a-b|<ε,则得到零点的近似值a或b;否则重复步骤(2)、(3)、(4).
考点训练
1.函数f(x)=+lg(3x+1)的定义域是 ( )
A. B. C. D.
【答案】B
【解析】由题意得解不等式组得-2.已知函数f(x)=且f(a)=-3,则f(6-a)=( )
A.- B.- C.- D.-
【答案】A
【解析】当a≤1,f(a)=2a-1-2=-3,显然不成立;
当a≥1,f(a)=-log2(a+1)=-3,解得a=7,满足条件.
故当a=7,f(6-a)=f(-1)=2-2-2=-.故选A.
3.若奇函数y=f(x)的图象关于直线x=2对称,且f(3)=3,则f(-1)= .
【答案】-3
【解析】y=f(x)的图象关于直线x=2对称,则f(3)=f(1)=3.
y=f(x)为奇函数,则f(-1)=-f(1)=-3.
4.函数f(x)=+的定义域为 ( )
A.[-2,0)∪(0,2] B.(-1,0)∪(0,2]
C.[-2,2] D.(-1,2]
【答案】B
【解析】由题意得
解不等式组得-15.设集合A={x|-3≤2x-1≤3},集合B是函数y=lg(x-1)的定义域,则A∩B= ( )
A.(1,2) B.[1,2] C.[1,2) D.(1,2]
【答案】D
【解析】由题意得x-1>0,解得x>1,则集合B={x|x>1}.
而集合A={x|-1≤x≤2},
于是A∩B={x|16.若函数f(x)=kx-ln x在区间(1,+∞)单调递增,则k的取值范围是( )
A.(-∞,-2] B.(-∞,-1]
C.[2,+∞) D.[1,+∞)
【答案】D
【解析】由函数f(x)=kx-ln x在区间(1,+∞)单调递增,
则当x>1时,f'(x)=k-≥0,即当x>1,k≥ 恒成立,
得到当x>1,k≥=1.故选D.
7.下列函数中,既是奇函数又是增函数的是 ( )
A.y=x+1 B.y=-x2 C.y= D.y=x|x|
【答案】D
【解析】选项A是增函数,但不是奇函数;
选项B是偶函数;
选项C是反比例函数,在第一象限和第三象限分别是单调递减的;
选项D既是奇函数又是增函数.
故选D.
8.下列函数中,在区间(0,+∞)上为增函数的是 ( )
A.y=ln(x+2) B.y=- C.y= D.y=x+
【答案】A
【解析】在区间(0,+∞)上为增函数的是y=ln(x+2);
选项B和选项C是减函数;
而选项D.y=x+在区间(0,1)上是减函数,在区间(1,+∞)上是增函数.故选A.
9.下列函数为偶函数的是 ( )
A.y=sin x B.y=x3
C.y=ex D.y=ln
【答案】D
【解析】观察可得,四个选项的定义域均为R,
且只有函数y=ln是偶函数.故选D.
10.若函数f(x)=3x+3-x与g(x)=3x-3-x的定义域均为R,则 ( )
A.f(x)与g(x)均为偶函数
B.f(x)为奇函数,g(x)为偶函数
C.f(x)与g(x)均为奇函数
D.f(x)为偶函数,g(x)为奇函数
【答案】D
【解析】 任意x∈R有,f(-x)=3-x+3x=f(x),故f(x)为偶函数;
g(-x)=3-x-3x=-(3x-3-x)=-g(x),故g(x)为奇函数.故选D.
11.若函数f(x)=为奇函数,则a= ( )
A. B. C. D.1
【答案】A
【解析】由f(x)为奇函数知,对于定义域内任意x有
f(-x)==-=-f(x),
即(-2x+1)(-x-a)=(2x+1)(x-a)在定义域内恒成立.
化简得2(2a-1)x=0,由于此式在定义域内恒成立,所以a=.故选A.
12.设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则f= ( )
A.- B.- C. D.
【答案】A
【解析】由f(x)周期为2可知,f=f=f,
由f(x)为奇函数知f=-f=-2××=-.故选A.
13.已知幂函数y=f(x)的图象过点,则log4f(2)的值为 ( )
A. B.- C.2 D.-2
【答案】A
【解析】设幂函数f(x)=xa,因为幂函数y=f(x)的图象过点,
所以有f==,于是有a=.即f(x)=,
从而有log4f(2)=log4=log42=×=.故选A.
14.若函数y=f(x)是函数y=ax(a>0,且a≠1)的反函数,且f(2)=1,则f(x)= ( )
A.log2x B. C. D.2x-2
【答案】A
【解析】由函数y=f(x)是函数y=ax(a>0,且a≠1)的反函数可知f(x)=logax,
所以有f(2)=loga2=1,于是a=2.故f(x)=log2x.故选A.
15.设函数f(x)是定义在R上的周期为2的偶函数,当x∈[0,1]时,
f(x)=x+1,则f= .
【答案】
【解析】由函数f(x)是定义在R上的周期为2的函数可知,
f=f=f.
由f(x)为偶函数知f=f=+1=.
16.若a>b>0,0A.logacC.accb
【答案】B
【解析】∵0∵a>b>0,∴logca17.已知y=f(x)是奇函数.若g(x)=f(x)+2,且g(1)=1,则g(-1)= .
【答案】3
【解析】由条件可知g(1)=f(1)+2=1,所以f(1)=-1.
又知y=f(x)是奇函数,故g(-1)=f(-1)+2=-f(1)+2=1+2=3.
18.设a=log54,b=(log53)2,c=log45,则a,b,c的大小关系是 ( )
A.aC.a【答案】D
【解析】由对数的性质可知,
a=log540所以(log53)2综上有b19.设a=,b=,c=,则a,b,c的大小关系是 ( )
A.a>c>b B.a>b>c
C.c>a>b D.b>c>a
【答案】A
【解析】根据指数函数性质,
因为0<<1,所以>,即c>b.
根据幂函数性质,因为>0,所以>,即a>c.故选A
20.若2a+log2a=4b+2log4b,则 ( )
A.a>2b B.a<2b C.a>b2 D.a【答案】B
【解析】因为2a+log2a=4b+2log4b=22b+log2b,
且22b+log2b<22b+log22b=22b+log2b+1,
所以2a+log2a<22b+log22b.
令f(x)=2x+log2x,
由指、对数函数的单调性可得f(x)在(0,+∞)内单调递增.
则由f(a)21.若a>0,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于 ( )
A.2 B.3 C.6 D.9
【答案】D
【解析】f'(x)=12x2-2ax-2b.
由f'(1)=12×12-2a×1-2b=0,得a+b=6.
根据a+b≥2(a>0,b>0),得到ab≤=9.故选D.
22.函数f(x)=ex+x-2的零点所在的一个区间是 ( )
A.(-2,-1) B.(-1,0) C.(0,1) D.(1,2)
【答案】C
【解析】f(0)=e0+0-2<0,f(1)=e1+1-2>0,
f(0)·f(1)<0.
故选C.
23.函数y=x2-ln x的单调递减区间为 ( )
A.(-1,1] B.(0,1] C.[1,+∞) D.(0,+∞)
【答案】B
【解析】y'=x-=,其中x>0,
当y'<0时,原函数单调递减,解得024.设函数f(x)=则使得f(x)≤2成立的x的取值范围是 .
【答案】(-∞,8]
【解析】当x<1时,由ex-1≤2可得x-1≤ln 2,即x≤ln 2+1,故x<1;
当x≥1时,由≤2可得x≤8,故1≤x≤8.
综上可得x≤8.
25.设函数f(x)=则f(f(3))= ( )
A. B.3 C. D.
【答案】D
【解析】因为f(3)=,所以有f(f(3))=f=+1=.故选D.
26.已知实数a≠0,函数f(x)=若f(1-a)=f(1+a),则a的值为 .
【答案】-
【解析】若1-a<1,那么a>0,则1+a>1,
f(1-a)=2(1-a)+a=-a+2,f(1+a)=-(a+1)-2a=-3a-1,
所以由-a+2=-3a-1,得a=-与假设前提矛盾;
由以上可知,f(1+a)=2(1+a)+a=3a+2,f(1-a)=-(1-a)-2a=-a-1,
所以由3a+2=-a-1,得4a=-3,即a=-.
27.若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则( )
A.a=1,b=1 B.a=-1,b=1
C.a=1,b=-1 D.a=-1,b=-1
【答案】A
【解析】对曲线y=x2+ax+b求导得y'=2x+a,斜率k=2x+a,切线方程x-y+1=0,
斜率为1,将点(0,b)分别代入得方程组为
解得a=1,b=1.故选A.
28.曲线y=x(3ln x+1)在点(1,1)处的切线方程为 .
【答案】y=4x-3
【解析】∵由y=x(3ln x+1)求导,得y'=3ln x+4.
把x=1代入得y'=4.
∴切线方程为y=4x-3.
29.若函数f(x)=ax3+x+1的图象在点(1,f(1))处的切线过点(2,7),则a= .
【答案】1
【解析】令函数图象在点(1,f(1))处的切线斜率为k,
由题得f'(x)=3ax2+1,可得k=f'(1)=3a+1.
又f(1)=a+2,故切点为(1,a+2).
又切线过(2,7),
由斜率公式知k==3a+1,解得a=1.
30.若过点(a,b)可以作曲线y=ex的两条切线,则 ( )
A.eb【答案】D
【解析】函数y=ex是增函数,y'=ex>0恒成立,函数的图象如图所示,y>0,即切点坐标在x轴上方.
如果点(a,b)在x轴下方,连线的斜率小于0,不成立;
如果点(a,b)在x轴或下方时,只有一条切线;
如果点(a,b)在曲线上,只有一条切线;
如果点(a,b)在曲线上侧,没有切线;
由图象可知(a,b)在图象的下方,并且在x轴上方时,有两条切线,可知0故选D.
31.设函数f(x)=则满足f(x+1)是 ( )
A.(-∞,-1] B.(0,+∞) C.(-1,0) D.(-∞,0)
【答案】D
【解析】函数f(x)=的图象如图所示.
满足f(x+1)故选D.
32.设a≠0,若x=a为函数f(x)=a(x-a)2(x-b)的极大值点,则 ( )
A.ab C.aba2
【答案】D
【解析】令f(x)=0,解得x=a或x=b,即x=a及x=b是f(x)的两个零点,
当a>0时,由三次函数的性质可知,要使x=a是f(x)的极大值点,则函数f(x)的大致图象如下图1所示,则0当a<0时,由三次函数的性质可知,要使x=a是f(x)的极大值点,则函数f(x)的大致图象如下图2所示,则b综上可得ab>a2.故选D.
(图1)
(图2)
33.已知函数f(x)=若关于x的方程f(x)=-x+a
(a∈R)恰有两个互异的实数解,则a的取值范围为 ( )
A. B.
C.∪{1} D.∪{1}
【答案】D
【解析】作出函数f(x)=的图象,以及直线y=-x的图象,
关于x的方程f(x)=-x+a(a∈R)恰有两个互异的实数解,
即为y=f(x)和y=-x+a的图象有两个交点.平移直线y=-x,
考虑直线经过点(1,2)和(1,1)时,有两个交点,可得a=或a=.
考虑直线与y=在x>1相切,可得ax-x2=1,
由Δ=a2-1=0,解得a=1(-1舍去).
综上可得a的范围是∪{1}.故选D.
34.已知函数f(x)=g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是 ( )
A.[-1,0) B.[0,+∞) C.[-1,+∞) D.[1,+∞)
【答案】C
【解析】由g(x)=0得f(x)=-x-a,
作出函数f(x)和y=-x-a的图象(如图所示).
当直线y=-x-a的截距-a≤1,即a≥-1时,
两个函数的图象都有2个交点,即函数g(x)存在2个零点.
故实数a的取值范围是[-1,+∞),故选C.
35.设a,b∈R,函数f(x)=若函数y=f(x)-ax-b恰有3个零点,则 ( )
A.a<-1,b<0 B.a<-1,b>0
C.a>-1,b<0 D.a>-1,b>0
【答案】C
【解析】当x<0时,由y=f(x)-ax-b=x-ax-b=(1-a)x-b=0,得x=,
可知y=f(x)-ax-b最多有一个零点;
当x≥0时,
y=f(x)-ax-b=x3-(a+1)x2+ax-ax-b=x3-(a+1)x2-b,y'=x2-(a+1)x,
【解析】当a+1≤0,即a≤-1时,y'≥0,y=f(x)-ax-b在[0,+∞)上递增,
y=f(x)-ax-b最多有一个零点,不合题意;
当a+1>0,即a>-1时,令y'>0得x∈(a+1,+∞),函数递增;
令y'<0得x∈[0,a+1),函数递减.函数最多有2个零点;
根据题意函数y=(x)-ax-b恰有3个零点 函数y=f(x)-ax-b在(-∞,0)上有一个零点,在[0,+∞)上有2个零点.
如上图所示,∴<0,
且
解得b<0,1-a>0,b>-(a+1)3.
∴-(a+1)336.设函数f(x)=x3cos x+1.若f(a)=11,则f(-a)= .
【答案】-9
【解析】∵f(a)=a3cos a+1=11,∴a3cos a=10.
∴f(-a)=-a3cos a+1=-10+1=-9.
37.函数f(x)=x3-3x2+1在x= 处取得极小值.
【答案】2
【解析】∵f'(x)=3x2-6x=3x(x-2),
∴f(x)的单调递增区间为(-∞,0),(2,+∞),递减区间为(0,2).
∴f(x)在x=2处取得极小值.
38.若函数y=x3-ax2+4在区间(0,2)内单调递减,则实数a的取值范围是 .
【答案】[3,+∞)
【解析】y'=3x2-2ax,由题意知3x2-2ax<0在区间(0,2)内恒成立,
即a>x在区间(0,2)上恒成立,
∴a≥3.答案为[3,+∞).
39.函数f(x)=2x3-3x2-12x+5在区间[0,3]上的最大值和最小值分别是 ( )
A.5,-15 B.5,-4 C.-4,-15 D.-5,-15
【答案】A
【解析】令f(x)'=6x2-6x-12=0,解得x=2或x=-1.
∵f(0)=5,f(2)=-15,f(3)=-4,
∴最大值为5,最小值为-15.故选A.
40.如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),其中g'(x)是g(x)的导函数,则g'(3)= .
【答案】0
【解析】∵直线l:y=kx+2是曲线y=f(x)在x=3处的切线,∴f(3)=1.
又点(3,1)在直线l上,∴3k+2=1,从而k=-.
∴k=f'(3)=-.∵g(x)=xf(x),∴g'(x)=f(x)+xf'(x).
则g'(3)=f(3)+3f'(3)=1+3×=0.故答案为0.
41.设函数y=f(x)的图象与y=2x+a的图象关于直线y=-x对称,且
f(-2)+f(-4)=1,则a= ( )
A.-1 B.1 C.2 D.4
【答案】C
【解析】设(x,y)是函数y=f(x)的图象上任意一点,它关于直线y=-x对称的点为(-y,-x),
由题可知(-y,-x)在函数y=2x+a的图象上,
∴由-x=2-y+a,解得y=-log2(-x)+a,即f(x)=-log2(-x)+a.
∴由f(-2)+f(-4)=-log22+a-log24+a=1,解得a=2.故选C.
42.已知函数f(x)=|ex-1|,x1<0,x2>0,函数f(x)的图象在点A(x1,f(x1))和点B(x2,f(x2))的两条切线互相垂直,且分别交y轴于M,N两点,则的取值范围是 .
【答案】(0,1)
【解析】当x<0时,f(x)=1-ex,导数为f'(x)=-ex,可得在点A(x1,1-)处的斜率为k1=-,切线AM的方程为y-(1-)=-(x-x1).
令x=0,可得y=1-+x1,即M(0,1-+x1);
当x>0时,f(x)=ex-1,导数为f'(x)=ex,可得在点B(x2,-1)处的斜率为k2=,切线BN的方程为y-(-1)=(x-x2).
令x=0,可得y=-1-x2,即N(0,-1-x2).
由f(x)的图象在点A,B处的切线相互垂直,可得k1k2=-·=-1,
即为x1+x2=0,且x1<0,x2>0,
所以===∈(0,1).
故答案为(0,1).
43.(多选题)若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称函数y=f(x)具有T性质,下列函数中具有T性质的是 ( )
A.y=cos x B.y=ln x C.y=ex D.y=x2
【答案】AD
【解析】由题意函数y=f(x)具有T性质,则存在x1,x2,使得f'(x1)f'(x2)=-1.
对于A,y=cos x的导数为y'=-sin x,存在x1=,x2=-,使得f'(x1)f'(x2)=-1;
对于B,y=ln x的导数为y'=>0,不存在x1,x2,使得f'(x1)f'(x2)=-1;
对于C,y=ex的导数y'=ex>0,不存在x1,x2,使得f'(x1)f'(x2)=-1;
对于D,y=x2的导数为y'=2x,存在x1=1,x2=-,使得f'(x1)f'(x2)=-1.
综上,具有性质T的函数为AD.故选AD.
44.(多选题)已知函数f(x)=ex-f(0)x+x2,则 ( )
A.f(0)=1
B.函数f(x)的极小值点为0
C.函数f(x)的单调递减区间是(0,+∞)
D. x∈R,不等式f(x)≥e恒成立
【答案】AB
【解析】在f(x)=ex-f(0)x+x2中,取x=0,可得f(0)=e0=1.故A正确;
∵f(x)=ex-x+x2,f'(x)=ex+x-1,f″(x)=ex+1>0,
∴f'(x)在(-∞,+∞)上为增函数.
∵f'(0)=e0-1=0,∴当x∈(-∞,0)时,f'(x)<0;当x∈(0,+∞)时,f'(x)>0,
则f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
∴f(x)的极小值为f(0)=e0=1,故B正确;C,D错误.故选AB.
45.(多选题)关于函数f(x)=+ln x,下列说法正确的是 ( )
A.f(1)是f(x)的极小值
B.函数y=f(x)-x有且只有1个零点
C.f(x)在(-∞,1)上单调递减
D.设g(x)=xf(x),则g【答案】ABD
【解析】对于C,函数f(x)的定义域为(0,+∞),故C错误;
对于A,f'(x)=-+=,
在(0,1)上f'(x)<0,f(x)单调递减;在(1,+∞)上,f'(x)>0,f(x)单调递增,
所以f(x)极小值=f(1)=1,故A正确;
对于B,y=f(x)-x=+ln x-x,y'=-+-1==<0,
所以函数y=f(x)-x=+ln x-x在(0,+∞)上单调递减,且当x=1时,y=f(1)-1=0,
所以y=f(x)-x有且只有一个零点,故B正确;
对于D,g(x)=xf(x)=1+xln x,g'(x)=x·+ln x=1+ln x,
所以在(e-1,+∞)上,g'(x)>0,g(x)单调递增;在(0,e-1)上,g'(x)<0,g(x)单调递减,
所以g(x)最小值=g(e-1)=g,
所以g46.(多选题)已知函数f(x)=ex+asin x,则 ( )
A.当a=-1时,f(x)在区间(0,+∞)上单调递增
B.当a=-1时,f(x)在区间(0,f(0))处的切线为x轴
C.当a=1时,f(x)在区间(-π,0)上存在唯一极小值点x0,且
-1D.对任意a>0,f(x)在区间(-π,+∞)上均存在零点
【答案】AC
【解析】对于A,当a=-1时,f(x)=ex-sin x,f'(x)=ex-cos x.
当x∈(0,+∞)时,f'(x)>0恒成立,f(x)在(0,+∞)上单调递增,故A正确;
对于B,f'(0)=e0-cos 0=1-1=0,而f(0)=e0-sin 0=1,
则f(x)在(0,f(0))处的切线为y=1,故B错误;
【解析】 对于C,当a=1时,f(x)=ex-sin x(-πf″(x)=ex-sin x>0恒成立,则f'(x)单调递增,
又f'=+cos<0,f'=>0,
故f(x)存在唯一极值点,
不妨设为x0∈,则f'(x0)=0,即+cos x0=0,
f(x0)=+sin x0=sin x0-cos x0=sin∈(-1,0),故C正确;
【解析】 对于D,
f(x)=ex+asin x,x∈(-π,+∞),令f(x)=0,即ex+asin x=0,
当x=kπ,k>-1且k∈Z时,显然没有零点;
∴a=-,令F(x)=-,F'(x)=-.
令F'(x)=0,解得x=kπ+,k≥-1,k∈Z.
∴x∈(k≥0,k∈Z)时,F(x)单调递减;
x∈时,F(x)单调递增.
F(x)有极小值f=≥.
x∈时,F(x)单调递增;
x∈时,f(x)单调递减.
F(x)有极大值f=-≤-,故D错误.故选AC.
47.(多选题)已知过点A(a,0)作曲线C:y=的切线有且仅有两条,则实数a的值可以是 ( )
A.-2 B.4 C.0 D.6
【答案】AD
【解析】设切点为,∵y'=,
∴在切点处的切线方程为y-=(x-x0).
把点A(a,0)代入,得-=(a-x0),化简得-ax0+a=0.
过点A点作曲线C的切线有且仅有两条,
即方程-ax0+a=0有两个解,则由Δ=a2-4a>0,解得a<0或a>4.
结合选项可知,a的值可以是-2,6.故选AD.
48.(多选题)已知函数f(x)=xln(2x+2-x),则以下结论正确的是( )
A.f(x)为奇函数
B.f(x)在区间(0,+∞)上单调递增
C.曲线y=f(x)在(0,f(0))处的切线的斜率为ln 2
D.函数f(x)有三个零点
【答案】ABC
【解析】对于A,函数f(x)的定义域为R,且有f(-x)=(-x)ln(2x+2-x)
=-xln(2x+2-x)=-f(x),则f(x)为奇函数,故A正确;
对于B,当x∈(0,+∞)时,y=x为增函数,而y=2x+2-x≥2,
则ln(2x+2-x)≥ln 2>0,
当x∈(0,+∞)时,y=2x+2-x为增函数,故函数f(x)=xln(2x+2-x)在区间(0,+∞)上单调递增.故B正确;
对于C,设h(x)=ln(2x+2-x),于是f(x)=xh(x),有f'(x)=x'h(x)+xh'(x),
得f'(0)=h(0)=ln 2,故C正确;
对于D,由f(x)=0,可得x=0或ln(2x+2-x)=0,由2x+2-x≥2,
可得f(x)只有一个零点,故D错误.故选ABC.
49.(多选题)已知a>0,b>0且ea+ln b>a+b,则下列结论一定正确的是 ( )
A.a>b B.ea>b C.ea+b>2 D.a+ln b>0
【答案】BC
【解析】取a=1,b=1,e1+ln 1=e,a+b=2,
满足a>0,b>0且ea+ln b>a+b,故选项A不一定成立;
取a=1,b=,e1+ln=e-1,a+b=1+,
满足a>0,b>0且ea+ln b>a+b,但a+ln b=1+ln=0,
故选项D不一定成立;
【解析】令f(x)=ex-x,则f'(x)=ex-1,
∵当x>0时,f'(x)>0,f(x)在(0,+∞)上单调递增,
当x<0时,f'(x)<0,f(x)在(-∞,0)上单调递减,
∴f(x)极小值=f(x)最小值=f(0)=1.
∵a>0,b>0且ea+ln b>a+b,
∴ea-a>b-ln b ea-a>eln b-ln b f(a)>f(ln b),
当a>ln b>0,则ea>eln b=b>e0=1,
∴ea>b.
当a>0>ln b,此时0b,故B正确;
【解析】先证明对任意的x1,x2∈R+且x1≠x2,<,
不妨设x2=,
令t=>1,即证ln t->0.
设M(t)=ln t->0,M'(t)=>0,
故函数M(t)在(1,+∞)上为增函数,当t>1时,M(t)>M(1)=0,
∴对任意的x1,x2∈R+且x1≠x2,<.
∵ea+ln b>a+b,∴ea-b>ln ea-ln b.
∴>>1.
∴ea+b>2,故C正确.故选BC.
专题六 函数与导数
【考试内容】 函数及其表示;函数的图象;函数的性质;指数函数;对数函数;幂函数;函数的零点;导数的应用
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 10 10 15 10 10 15 10
全国卷(乙卷) 15 15 15 15 10 15 10
新高考全国Ⅰ卷 15 20
新高考全国Ⅱ卷 15 10
重要考点回顾
一、函数的基本性质
1.函数的单调性:
(1)f(x)在区间M上是增函数 x1,x2∈M,当x1
(记忆方法:不等号相同为增,不同为减,即同增异减)
2.函数的奇偶性:
(1)奇函数、偶函数的定义:
如果对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),则称函数y=f(x)是偶函数;
如果对于函数f(x)的定义域内的任意一个x,都有f(-x)=-f(x),则称函数y=f(x)是奇函数.
(2)奇、偶函数的性质:
①偶函数的图象关于y轴对称;奇函数的图象关于原点对称.
②奇函数f(x)的定义域中若含有0,则必有f(0)=0.
(3)常见的奇函数与偶函数:
①常见的奇函数:
正比例函数:f(x)=kx(x∈R);
反比例函数:f(x)=(x∈(-∞,0)∪(0,+∞));
正弦函数:f(x)=sin x(x∈R);
正切函数:f(x)=tan x
幂函数:f(x) =xn(x∈R)当n为奇数时f(x)=xn为奇函数.
几种特殊的奇函数:
②常见的偶函数:
余弦函数:f(x)=cosx(x∈R);
幂函数:f(x)=xn(x∈R)当n为偶数时f(x)=xn为偶函数.
几种特殊的偶函数:
f(x)=c(c为常数); f(x)=|x|;
f(x)= ; f(x)=|x+1|+|x-1|.
③在定义域符合要求的前提下:
奇函数与奇函数的和是奇函数;偶函数与偶函数的和是偶函数;
奇函数与奇函数的积是偶函数;偶函数与偶函数的积是偶函数;
奇函数与偶函数的积是奇函数;
奇函数与偶函数的和是非奇非偶函数;
如:f(x)=ax3+bx,f(x)=ax+ 是奇函数;
f(x)=ax2+c,f(x)= ax4+bx2+c,f(x)= ·x是偶函数;
f(x)=x2-x+1是非奇非偶函数.
3.函数的周期性:
(1)定义:对定义域内的任意x,若有f(x+T)=f(x)(其中T为非零常数),则称函数f(x)为周期函数,T为它的一个周期.所有正周期中最小的称为函数的最小正周期.如没有特别说明,文中所指的周期都指最小正周期.
(2)三角函数的最小正周期:
①y=sin x:T=2π; ②y=cos x:T=2π;
③y=tan x:T=π; ④y=Asin(ωx+φ),y=Acos(ωx+φ):T= ;
⑤y=tan ωx:T=
4.函数定义域的求法:列出使函数有意义的自变量的不等关系式,求解即可求得函数的定义域.常涉及的依据为:
①分母不为0;
②偶次根式中被开方数不小于0;
③对数的真数大于0,底数大于0且不等于1;
④零指数幂的底数不等于0;
⑤实际问题要考虑实际意义.
二、基本初等函数
指数、对数的运算性质:
(1)幂的运算性质:aman=am+n; (am)n=amn; (ab)m=ambm;
a0=1(a≠0);
(2)对数的概念:一般地,如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作:logaN
其中a叫做对数的底数,N叫做对数的真数.
以10为底的对数叫做常用对数;记作:lg.
以e为底的对数叫做自然对数;记作:ln.
(3)对数的简单性质:
①负数和零没有对数;
②底的对数是1,即logaa=1;
③1的对数是零,即loga1=0.
(4)对数的运算法则:如果a>0,且a≠1,M>0,N>0,那么:
①loga(MN)=logaM+logaN;
②loga( )=logaM-logaN;
③logaMn=nlogaM(n∈R);
④logab= (a>0,且a≠1,c>0,且c≠1,b>0)(对数换底公式);
⑤对数恒等式:
(5)幂函数:一般地,函数y=xa叫做幂函数.其中x是自变量,a是常数.
要求:掌握a=1,2,3, ,-1时的函数图象.
y=x y=x2 y=x3 y=x-1
定义域 R R R [0,+∞) (-∞,0)∪(0,+∞)
值域 R [0,+∞) R [0,+∞) (-∞,0)∪(0,+∞)
奇偶性 奇函数 偶函数 奇函数 非奇非偶函数 奇函数
单调性 增 (-∞,0)减 (0,+∞)增 增 增 (-∞,0)减
(0,+∞)减
公共点 (1,1)
图象:
(6)指数函数:y=ax(a>0,a≠1)
图象恒过点(0,1),单调性与a的值有关,在解题中,往往要对a分a>1和0
图象恒过点(1,0),单调性与a的值有关,在解题中,往往要对a分a>1和0
一般形式 y=ax(a>0,a≠1) y=logax(a>0,a≠1)
定义域 R (0,+∞)
值域 (0,+∞) R
单调性 a>1 单调递增 a>1 单调递增
0
图象
(8)注意的几个问题:
①y=ax与y=logax 的图象关系是关于直线y=x对称;这两个函数互为反函数.
②比较两个指数式或对数式的大小的基本方法是构造相应的指数或对数函数,若底数不相同时转化为同底数的指数或对数,还要注意与1或0比较.
三、导数
1.意义:函数f(x)在点P处的导数就是函数f(x)的图象在点P处的切线的斜率.
即:k=f'(x0)表示过曲线y=f(x)上的点P(x0,f(x0))的切线的斜率.
2.几种常见的函数导数:
①C'=0(C为常数) ⑤(ln x)'=
②(xn)'=nxn-1(n∈R) ⑥(logax)'=
③(sin x)'=cos x ⑦(ex)'=ex
④(cos x)'=-sin x ⑧(ax)'=axln a
3.求导数的四则运算法则:
[f(x)±g(x)]'=f'(x)±g'(x);
[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x);
4.导数的应用:
(1)求切线的斜率,以及求切线方程.
(2)利用导数判断函数的单调性:
若f'(x)>0,x∈(a,b)则f(x)在(a,b)上为增函数;
若f'(x)<0,x∈(a,b)则f(x)在(a,b)上为减函数.
(3)单调区间的求解过程,已知y=f(x)
①分析y=f(x)的定义域;
②求导数y'=f'(x);
③解不等式f'(x)>0,解集在定义域内的部分为增区间;
④解不等式f'(x)<0,解集在定义域内的部分为减区间.
(4)求极值、求最值.
①求函数y=f(x)的极值的方法:
先解方程f'(x)=0,当f'(x0)=0时:
(Ⅰ)如果在x0附近的左侧f'(x)>0,右侧f'(x)<0,那么f(x0)是极大值;
(Ⅱ)如果在x0附近的左侧f'(x)<0,右侧f'(x)>0,那么f(x0)是极小值.
②求函数y=f(x)在[a,b]上的最值的步骤:
(Ⅰ)求函数y=f(x)在(a,b)内的极值;
(Ⅱ)将函数y=f(x)的各极值与端点处的函数值f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
注意:
(1)若当x=x0时函数f(x)有极值,必有f'(x0)=0.但反之不成立;
(2)若函数f(x)在[a,b]上单调递增,则f(a)为函数的最小值,f(b)为函数的最大值;
函数f(x)在[a,b]上单调递减,则f(a)为函数的最大值,f(b)为函数的最小值.
四、函数的零点及二分法
1.对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)的图象与x轴的交点的横坐标.即:
方程f(x)=0有实数根 函数y=f(x)的图象与x轴有交点 函数y=f(x)有零点.
2.定理:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有:f(a)f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
3.二分法的定义:对于在区间[a,b]上连续不断且f(a)f(b)<0的函数y=f(x),通过不断地把函数f(x)所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
4.二分法的步骤:
(1)确定区间[a,b],验证f(a)f(b)<0,给定精确度ε;
(2)求区间的中点x1;
(3)计算f(x1):
①若f(x1)=0,则x1就是函数的零点;
②若f(a)f(x1)<0,则令b=x1(此时零点x0∈(a,x1));
③若f(a)f(x1)>0,则令a=x1(此时零点x0∈(x1,b)).
(4)判断是否达到精确度ε:即|a-b|<ε,则得到零点的近似值a或b;否则重复步骤(2)、(3)、(4).
考点训练
1.函数f(x)=+lg(3x+1)的定义域是 ( )
A. B. C. D.
【答案】B
【解析】由题意得解不等式组得-
A.- B.- C.- D.-
【答案】A
【解析】当a≤1,f(a)=2a-1-2=-3,显然不成立;
当a≥1,f(a)=-log2(a+1)=-3,解得a=7,满足条件.
故当a=7,f(6-a)=f(-1)=2-2-2=-.故选A.
3.若奇函数y=f(x)的图象关于直线x=2对称,且f(3)=3,则f(-1)= .
【答案】-3
【解析】y=f(x)的图象关于直线x=2对称,则f(3)=f(1)=3.
y=f(x)为奇函数,则f(-1)=-f(1)=-3.
4.函数f(x)=+的定义域为 ( )
A.[-2,0)∪(0,2] B.(-1,0)∪(0,2]
C.[-2,2] D.(-1,2]
【答案】B
【解析】由题意得
解不等式组得-1
A.(1,2) B.[1,2] C.[1,2) D.(1,2]
【答案】D
【解析】由题意得x-1>0,解得x>1,则集合B={x|x>1}.
而集合A={x|-1≤x≤2},
于是A∩B={x|1
A.(-∞,-2] B.(-∞,-1]
C.[2,+∞) D.[1,+∞)
【答案】D
【解析】由函数f(x)=kx-ln x在区间(1,+∞)单调递增,
则当x>1时,f'(x)=k-≥0,即当x>1,k≥ 恒成立,
得到当x>1,k≥=1.故选D.
7.下列函数中,既是奇函数又是增函数的是 ( )
A.y=x+1 B.y=-x2 C.y= D.y=x|x|
【答案】D
【解析】选项A是增函数,但不是奇函数;
选项B是偶函数;
选项C是反比例函数,在第一象限和第三象限分别是单调递减的;
选项D既是奇函数又是增函数.
故选D.
8.下列函数中,在区间(0,+∞)上为增函数的是 ( )
A.y=ln(x+2) B.y=- C.y= D.y=x+
【答案】A
【解析】在区间(0,+∞)上为增函数的是y=ln(x+2);
选项B和选项C是减函数;
而选项D.y=x+在区间(0,1)上是减函数,在区间(1,+∞)上是增函数.故选A.
9.下列函数为偶函数的是 ( )
A.y=sin x B.y=x3
C.y=ex D.y=ln
【答案】D
【解析】观察可得,四个选项的定义域均为R,
且只有函数y=ln是偶函数.故选D.
10.若函数f(x)=3x+3-x与g(x)=3x-3-x的定义域均为R,则 ( )
A.f(x)与g(x)均为偶函数
B.f(x)为奇函数,g(x)为偶函数
C.f(x)与g(x)均为奇函数
D.f(x)为偶函数,g(x)为奇函数
【答案】D
【解析】 任意x∈R有,f(-x)=3-x+3x=f(x),故f(x)为偶函数;
g(-x)=3-x-3x=-(3x-3-x)=-g(x),故g(x)为奇函数.故选D.
11.若函数f(x)=为奇函数,则a= ( )
A. B. C. D.1
【答案】A
【解析】由f(x)为奇函数知,对于定义域内任意x有
f(-x)==-=-f(x),
即(-2x+1)(-x-a)=(2x+1)(x-a)在定义域内恒成立.
化简得2(2a-1)x=0,由于此式在定义域内恒成立,所以a=.故选A.
12.设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则f= ( )
A.- B.- C. D.
【答案】A
【解析】由f(x)周期为2可知,f=f=f,
由f(x)为奇函数知f=-f=-2××=-.故选A.
13.已知幂函数y=f(x)的图象过点,则log4f(2)的值为 ( )
A. B.- C.2 D.-2
【答案】A
【解析】设幂函数f(x)=xa,因为幂函数y=f(x)的图象过点,
所以有f==,于是有a=.即f(x)=,
从而有log4f(2)=log4=log42=×=.故选A.
14.若函数y=f(x)是函数y=ax(a>0,且a≠1)的反函数,且f(2)=1,则f(x)= ( )
A.log2x B. C. D.2x-2
【答案】A
【解析】由函数y=f(x)是函数y=ax(a>0,且a≠1)的反函数可知f(x)=logax,
所以有f(2)=loga2=1,于是a=2.故f(x)=log2x.故选A.
15.设函数f(x)是定义在R上的周期为2的偶函数,当x∈[0,1]时,
f(x)=x+1,则f= .
【答案】
【解析】由函数f(x)是定义在R上的周期为2的函数可知,
f=f=f.
由f(x)为偶函数知f=f=+1=.
16.若a>b>0,0
【答案】B
【解析】∵0
【答案】3
【解析】由条件可知g(1)=f(1)+2=1,所以f(1)=-1.
又知y=f(x)是奇函数,故g(-1)=f(-1)+2=-f(1)+2=1+2=3.
18.设a=log54,b=(log53)2,c=log45,则a,b,c的大小关系是 ( )
A.a
【解析】由对数的性质可知,
a=log54
A.a>c>b B.a>b>c
C.c>a>b D.b>c>a
【答案】A
【解析】根据指数函数性质,
因为0<<1,所以>,即c>b.
根据幂函数性质,因为>0,所以>,即a>c.故选A
20.若2a+log2a=4b+2log4b,则 ( )
A.a>2b B.a<2b C.a>b2 D.a
【解析】因为2a+log2a=4b+2log4b=22b+log2b,
且22b+log2b<22b+log22b=22b+log2b+1,
所以2a+log2a<22b+log22b.
令f(x)=2x+log2x,
由指、对数函数的单调性可得f(x)在(0,+∞)内单调递增.
则由f(a)
A.2 B.3 C.6 D.9
【答案】D
【解析】f'(x)=12x2-2ax-2b.
由f'(1)=12×12-2a×1-2b=0,得a+b=6.
根据a+b≥2(a>0,b>0),得到ab≤=9.故选D.
22.函数f(x)=ex+x-2的零点所在的一个区间是 ( )
A.(-2,-1) B.(-1,0) C.(0,1) D.(1,2)
【答案】C
【解析】f(0)=e0+0-2<0,f(1)=e1+1-2>0,
f(0)·f(1)<0.
故选C.
23.函数y=x2-ln x的单调递减区间为 ( )
A.(-1,1] B.(0,1] C.[1,+∞) D.(0,+∞)
【答案】B
【解析】y'=x-=,其中x>0,
当y'<0时,原函数单调递减,解得0
【答案】(-∞,8]
【解析】当x<1时,由ex-1≤2可得x-1≤ln 2,即x≤ln 2+1,故x<1;
当x≥1时,由≤2可得x≤8,故1≤x≤8.
综上可得x≤8.
25.设函数f(x)=则f(f(3))= ( )
A. B.3 C. D.
【答案】D
【解析】因为f(3)=,所以有f(f(3))=f=+1=.故选D.
26.已知实数a≠0,函数f(x)=若f(1-a)=f(1+a),则a的值为 .
【答案】-
【解析】若1-a<1,那么a>0,则1+a>1,
f(1-a)=2(1-a)+a=-a+2,f(1+a)=-(a+1)-2a=-3a-1,
所以由-a+2=-3a-1,得a=-与假设前提矛盾;
由以上可知,f(1+a)=2(1+a)+a=3a+2,f(1-a)=-(1-a)-2a=-a-1,
所以由3a+2=-a-1,得4a=-3,即a=-.
27.若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则( )
A.a=1,b=1 B.a=-1,b=1
C.a=1,b=-1 D.a=-1,b=-1
【答案】A
【解析】对曲线y=x2+ax+b求导得y'=2x+a,斜率k=2x+a,切线方程x-y+1=0,
斜率为1,将点(0,b)分别代入得方程组为
解得a=1,b=1.故选A.
28.曲线y=x(3ln x+1)在点(1,1)处的切线方程为 .
【答案】y=4x-3
【解析】∵由y=x(3ln x+1)求导,得y'=3ln x+4.
把x=1代入得y'=4.
∴切线方程为y=4x-3.
29.若函数f(x)=ax3+x+1的图象在点(1,f(1))处的切线过点(2,7),则a= .
【答案】1
【解析】令函数图象在点(1,f(1))处的切线斜率为k,
由题得f'(x)=3ax2+1,可得k=f'(1)=3a+1.
又f(1)=a+2,故切点为(1,a+2).
又切线过(2,7),
由斜率公式知k==3a+1,解得a=1.
30.若过点(a,b)可以作曲线y=ex的两条切线,则 ( )
A.eb【答案】D
【解析】函数y=ex是增函数,y'=ex>0恒成立,函数的图象如图所示,y>0,即切点坐标在x轴上方.
如果点(a,b)在x轴下方,连线的斜率小于0,不成立;
如果点(a,b)在x轴或下方时,只有一条切线;
如果点(a,b)在曲线上,只有一条切线;
如果点(a,b)在曲线上侧,没有切线;
由图象可知(a,b)在图象的下方,并且在x轴上方时,有两条切线,可知0
31.设函数f(x)=则满足f(x+1)
A.(-∞,-1] B.(0,+∞) C.(-1,0) D.(-∞,0)
【答案】D
【解析】函数f(x)=的图象如图所示.
满足f(x+1)
32.设a≠0,若x=a为函数f(x)=a(x-a)2(x-b)的极大值点,则 ( )
A.ab C.ab
【答案】D
【解析】令f(x)=0,解得x=a或x=b,即x=a及x=b是f(x)的两个零点,
当a>0时,由三次函数的性质可知,要使x=a是f(x)的极大值点,则函数f(x)的大致图象如下图1所示,则0
(图1)
(图2)
33.已知函数f(x)=若关于x的方程f(x)=-x+a
(a∈R)恰有两个互异的实数解,则a的取值范围为 ( )
A. B.
C.∪{1} D.∪{1}
【答案】D
【解析】作出函数f(x)=的图象,以及直线y=-x的图象,
关于x的方程f(x)=-x+a(a∈R)恰有两个互异的实数解,
即为y=f(x)和y=-x+a的图象有两个交点.平移直线y=-x,
考虑直线经过点(1,2)和(1,1)时,有两个交点,可得a=或a=.
考虑直线与y=在x>1相切,可得ax-x2=1,
由Δ=a2-1=0,解得a=1(-1舍去).
综上可得a的范围是∪{1}.故选D.
34.已知函数f(x)=g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是 ( )
A.[-1,0) B.[0,+∞) C.[-1,+∞) D.[1,+∞)
【答案】C
【解析】由g(x)=0得f(x)=-x-a,
作出函数f(x)和y=-x-a的图象(如图所示).
当直线y=-x-a的截距-a≤1,即a≥-1时,
两个函数的图象都有2个交点,即函数g(x)存在2个零点.
故实数a的取值范围是[-1,+∞),故选C.
35.设a,b∈R,函数f(x)=若函数y=f(x)-ax-b恰有3个零点,则 ( )
A.a<-1,b<0 B.a<-1,b>0
C.a>-1,b<0 D.a>-1,b>0
【答案】C
【解析】当x<0时,由y=f(x)-ax-b=x-ax-b=(1-a)x-b=0,得x=,
可知y=f(x)-ax-b最多有一个零点;
当x≥0时,
y=f(x)-ax-b=x3-(a+1)x2+ax-ax-b=x3-(a+1)x2-b,y'=x2-(a+1)x,
【解析】当a+1≤0,即a≤-1时,y'≥0,y=f(x)-ax-b在[0,+∞)上递增,
y=f(x)-ax-b最多有一个零点,不合题意;
当a+1>0,即a>-1时,令y'>0得x∈(a+1,+∞),函数递增;
令y'<0得x∈[0,a+1),函数递减.函数最多有2个零点;
根据题意函数y=(x)-ax-b恰有3个零点 函数y=f(x)-ax-b在(-∞,0)上有一个零点,在[0,+∞)上有2个零点.
如上图所示,∴<0,
且
解得b<0,1-a>0,b>-(a+1)3.
∴-(a+1)3
【答案】-9
【解析】∵f(a)=a3cos a+1=11,∴a3cos a=10.
∴f(-a)=-a3cos a+1=-10+1=-9.
37.函数f(x)=x3-3x2+1在x= 处取得极小值.
【答案】2
【解析】∵f'(x)=3x2-6x=3x(x-2),
∴f(x)的单调递增区间为(-∞,0),(2,+∞),递减区间为(0,2).
∴f(x)在x=2处取得极小值.
38.若函数y=x3-ax2+4在区间(0,2)内单调递减,则实数a的取值范围是 .
【答案】[3,+∞)
【解析】y'=3x2-2ax,由题意知3x2-2ax<0在区间(0,2)内恒成立,
即a>x在区间(0,2)上恒成立,
∴a≥3.答案为[3,+∞).
39.函数f(x)=2x3-3x2-12x+5在区间[0,3]上的最大值和最小值分别是 ( )
A.5,-15 B.5,-4 C.-4,-15 D.-5,-15
【答案】A
【解析】令f(x)'=6x2-6x-12=0,解得x=2或x=-1.
∵f(0)=5,f(2)=-15,f(3)=-4,
∴最大值为5,最小值为-15.故选A.
40.如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),其中g'(x)是g(x)的导函数,则g'(3)= .
【答案】0
【解析】∵直线l:y=kx+2是曲线y=f(x)在x=3处的切线,∴f(3)=1.
又点(3,1)在直线l上,∴3k+2=1,从而k=-.
∴k=f'(3)=-.∵g(x)=xf(x),∴g'(x)=f(x)+xf'(x).
则g'(3)=f(3)+3f'(3)=1+3×=0.故答案为0.
41.设函数y=f(x)的图象与y=2x+a的图象关于直线y=-x对称,且
f(-2)+f(-4)=1,则a= ( )
A.-1 B.1 C.2 D.4
【答案】C
【解析】设(x,y)是函数y=f(x)的图象上任意一点,它关于直线y=-x对称的点为(-y,-x),
由题可知(-y,-x)在函数y=2x+a的图象上,
∴由-x=2-y+a,解得y=-log2(-x)+a,即f(x)=-log2(-x)+a.
∴由f(-2)+f(-4)=-log22+a-log24+a=1,解得a=2.故选C.
42.已知函数f(x)=|ex-1|,x1<0,x2>0,函数f(x)的图象在点A(x1,f(x1))和点B(x2,f(x2))的两条切线互相垂直,且分别交y轴于M,N两点,则的取值范围是 .
【答案】(0,1)
【解析】当x<0时,f(x)=1-ex,导数为f'(x)=-ex,可得在点A(x1,1-)处的斜率为k1=-,切线AM的方程为y-(1-)=-(x-x1).
令x=0,可得y=1-+x1,即M(0,1-+x1);
当x>0时,f(x)=ex-1,导数为f'(x)=ex,可得在点B(x2,-1)处的斜率为k2=,切线BN的方程为y-(-1)=(x-x2).
令x=0,可得y=-1-x2,即N(0,-1-x2).
由f(x)的图象在点A,B处的切线相互垂直,可得k1k2=-·=-1,
即为x1+x2=0,且x1<0,x2>0,
所以===∈(0,1).
故答案为(0,1).
43.(多选题)若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称函数y=f(x)具有T性质,下列函数中具有T性质的是 ( )
A.y=cos x B.y=ln x C.y=ex D.y=x2
【答案】AD
【解析】由题意函数y=f(x)具有T性质,则存在x1,x2,使得f'(x1)f'(x2)=-1.
对于A,y=cos x的导数为y'=-sin x,存在x1=,x2=-,使得f'(x1)f'(x2)=-1;
对于B,y=ln x的导数为y'=>0,不存在x1,x2,使得f'(x1)f'(x2)=-1;
对于C,y=ex的导数y'=ex>0,不存在x1,x2,使得f'(x1)f'(x2)=-1;
对于D,y=x2的导数为y'=2x,存在x1=1,x2=-,使得f'(x1)f'(x2)=-1.
综上,具有性质T的函数为AD.故选AD.
44.(多选题)已知函数f(x)=ex-f(0)x+x2,则 ( )
A.f(0)=1
B.函数f(x)的极小值点为0
C.函数f(x)的单调递减区间是(0,+∞)
D. x∈R,不等式f(x)≥e恒成立
【答案】AB
【解析】在f(x)=ex-f(0)x+x2中,取x=0,可得f(0)=e0=1.故A正确;
∵f(x)=ex-x+x2,f'(x)=ex+x-1,f″(x)=ex+1>0,
∴f'(x)在(-∞,+∞)上为增函数.
∵f'(0)=e0-1=0,∴当x∈(-∞,0)时,f'(x)<0;当x∈(0,+∞)时,f'(x)>0,
则f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
∴f(x)的极小值为f(0)=e0=1,故B正确;C,D错误.故选AB.
45.(多选题)关于函数f(x)=+ln x,下列说法正确的是 ( )
A.f(1)是f(x)的极小值
B.函数y=f(x)-x有且只有1个零点
C.f(x)在(-∞,1)上单调递减
D.设g(x)=xf(x),则g
【解析】对于C,函数f(x)的定义域为(0,+∞),故C错误;
对于A,f'(x)=-+=,
在(0,1)上f'(x)<0,f(x)单调递减;在(1,+∞)上,f'(x)>0,f(x)单调递增,
所以f(x)极小值=f(1)=1,故A正确;
对于B,y=f(x)-x=+ln x-x,y'=-+-1==<0,
所以函数y=f(x)-x=+ln x-x在(0,+∞)上单调递减,且当x=1时,y=f(1)-1=0,
所以y=f(x)-x有且只有一个零点,故B正确;
对于D,g(x)=xf(x)=1+xln x,g'(x)=x·+ln x=1+ln x,
所以在(e-1,+∞)上,g'(x)>0,g(x)单调递增;在(0,e-1)上,g'(x)<0,g(x)单调递减,
所以g(x)最小值=g(e-1)=g,
所以g
A.当a=-1时,f(x)在区间(0,+∞)上单调递增
B.当a=-1时,f(x)在区间(0,f(0))处的切线为x轴
C.当a=1时,f(x)在区间(-π,0)上存在唯一极小值点x0,且
-1
【答案】AC
【解析】对于A,当a=-1时,f(x)=ex-sin x,f'(x)=ex-cos x.
当x∈(0,+∞)时,f'(x)>0恒成立,f(x)在(0,+∞)上单调递增,故A正确;
对于B,f'(0)=e0-cos 0=1-1=0,而f(0)=e0-sin 0=1,
则f(x)在(0,f(0))处的切线为y=1,故B错误;
【解析】 对于C,当a=1时,f(x)=ex-sin x(-π
又f'=+cos<0,f'=>0,
故f(x)存在唯一极值点,
不妨设为x0∈,则f'(x0)=0,即+cos x0=0,
f(x0)=+sin x0=sin x0-cos x0=sin∈(-1,0),故C正确;
【解析】 对于D,
f(x)=ex+asin x,x∈(-π,+∞),令f(x)=0,即ex+asin x=0,
当x=kπ,k>-1且k∈Z时,显然没有零点;
∴a=-,令F(x)=-,F'(x)=-.
令F'(x)=0,解得x=kπ+,k≥-1,k∈Z.
∴x∈(k≥0,k∈Z)时,F(x)单调递减;
x∈时,F(x)单调递增.
F(x)有极小值f=≥.
x∈时,F(x)单调递增;
x∈时,f(x)单调递减.
F(x)有极大值f=-≤-,故D错误.故选AC.
47.(多选题)已知过点A(a,0)作曲线C:y=的切线有且仅有两条,则实数a的值可以是 ( )
A.-2 B.4 C.0 D.6
【答案】AD
【解析】设切点为,∵y'=,
∴在切点处的切线方程为y-=(x-x0).
把点A(a,0)代入,得-=(a-x0),化简得-ax0+a=0.
过点A点作曲线C的切线有且仅有两条,
即方程-ax0+a=0有两个解,则由Δ=a2-4a>0,解得a<0或a>4.
结合选项可知,a的值可以是-2,6.故选AD.
48.(多选题)已知函数f(x)=xln(2x+2-x),则以下结论正确的是( )
A.f(x)为奇函数
B.f(x)在区间(0,+∞)上单调递增
C.曲线y=f(x)在(0,f(0))处的切线的斜率为ln 2
D.函数f(x)有三个零点
【答案】ABC
【解析】对于A,函数f(x)的定义域为R,且有f(-x)=(-x)ln(2x+2-x)
=-xln(2x+2-x)=-f(x),则f(x)为奇函数,故A正确;
对于B,当x∈(0,+∞)时,y=x为增函数,而y=2x+2-x≥2,
则ln(2x+2-x)≥ln 2>0,
当x∈(0,+∞)时,y=2x+2-x为增函数,故函数f(x)=xln(2x+2-x)在区间(0,+∞)上单调递增.故B正确;
对于C,设h(x)=ln(2x+2-x),于是f(x)=xh(x),有f'(x)=x'h(x)+xh'(x),
得f'(0)=h(0)=ln 2,故C正确;
对于D,由f(x)=0,可得x=0或ln(2x+2-x)=0,由2x+2-x≥2,
可得f(x)只有一个零点,故D错误.故选ABC.
49.(多选题)已知a>0,b>0且ea+ln b>a+b,则下列结论一定正确的是 ( )
A.a>b B.ea>b C.ea+b>2 D.a+ln b>0
【答案】BC
【解析】取a=1,b=1,e1+ln 1=e,a+b=2,
满足a>0,b>0且ea+ln b>a+b,故选项A不一定成立;
取a=1,b=,e1+ln=e-1,a+b=1+,
满足a>0,b>0且ea+ln b>a+b,但a+ln b=1+ln=0,
故选项D不一定成立;
【解析】令f(x)=ex-x,则f'(x)=ex-1,
∵当x>0时,f'(x)>0,f(x)在(0,+∞)上单调递增,
当x<0时,f'(x)<0,f(x)在(-∞,0)上单调递减,
∴f(x)极小值=f(x)最小值=f(0)=1.
∵a>0,b>0且ea+ln b>a+b,
∴ea-a>b-ln b ea-a>eln b-ln b f(a)>f(ln b),
当a>ln b>0,则ea>eln b=b>e0=1,
∴ea>b.
当a>0>ln b,此时0
【解析】先证明对任意的x1,x2∈R+且x1≠x2,<,
不妨设x2
令t=>1,即证ln t->0.
设M(t)=ln t->0,M'(t)=>0,
故函数M(t)在(1,+∞)上为增函数,当t>1时,M(t)>M(1)=0,
∴对任意的x1,x2∈R+且x1≠x2,<.
∵ea+ln b>a+b,∴ea-b>ln ea-ln b.
∴>>1.
∴ea+b>2,故C正确.故选BC.
同课章节目录
