2023年高考数学客观题专题一 集合与逻辑用语 课件(共46张PPT)
文档属性
| 名称 | 2023年高考数学客观题专题一 集合与逻辑用语 课件(共46张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 12:30:04 | ||
图片预览








文档简介
(共46张PPT)
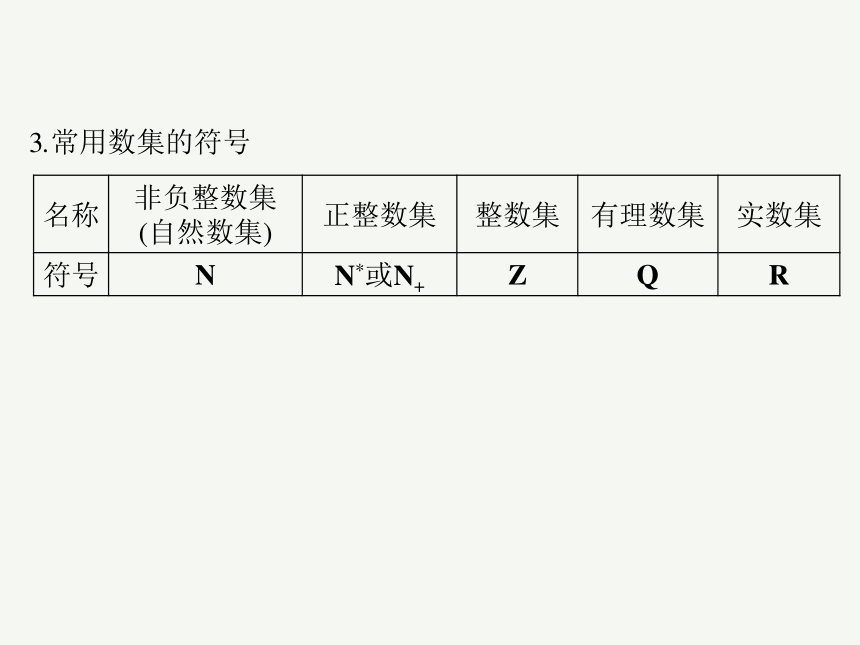
专题一 集合与逻辑用语
【考试内容】 集合;子集;补集;交集;并集;逻辑联结词;四种命题;充分条件;必要条件
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 10 5 5 5 5 5 5
全国卷(乙卷) 5 5 5 5 5 10 5
新高考全国Ⅰ卷 5 5
新高考全国Ⅱ卷 5 5
重要考点回顾
一、常用符号及其含义
1.元素与集合的关系是:属于或不属于关系,用符号∈或 表示.
2.集合与集合的关系:用 , ,=表示;A是B的子集记为A B;
A是B的真子集记为A B.特别地:
①任何一个集合是它本身的子集,记为A A;
②空集是任何集合的子集,记为 A;空集是任何非空集合的真子集;
③如果A B,同时B A,那么A=B;如果A B,B C,那么A C.
④n个元素的集合子集有2n个;n个元素的集合真子集有2n-1个;
n个元素的集合非空真子集有2n-2个.
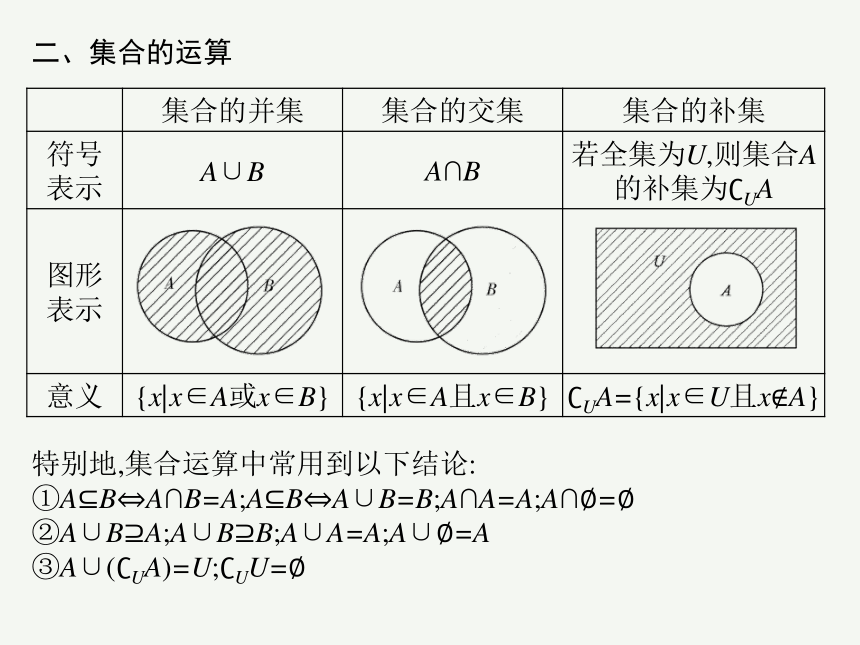
3.常用数集的符号
名称 非负整数集 (自然数集) 正整数集 整数集 有理数集 实数集
符号 N N*或N+ Z Q R
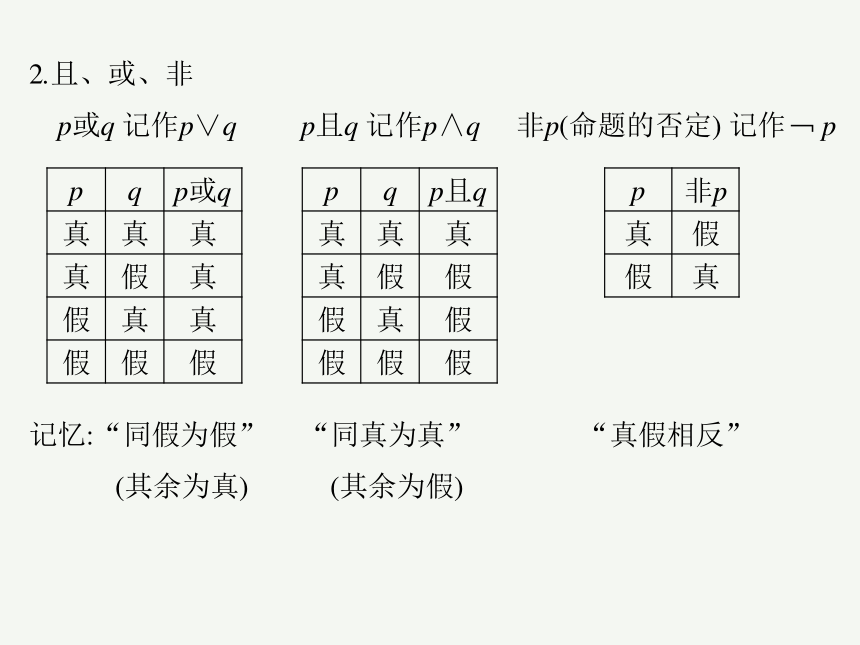
二、集合的运算
特别地,集合运算中常用到以下结论:
①A B A∩B=A;A B A∪B=B;A∩A=A;A∩ =
②A∪B A;A∪B B;A∪A=A;A∪ =A
③A∪( UA)=U; UU=
集合的并集 集合的交集 集合的补集
符号 表示 A∪B A∩B 若全集为U,则集合A的补集为 UA
图形 表示
意义 {x|x∈A或x∈B} {x|x∈A且x∈B} UA={x|x∈U且x A}
三、命题与简易逻辑
1.充要条件的判断:如果p q,则p是q的充分条件;
如果q p,则p是q的必要条件;
如果既有p q,又有q p,记作p q,则p是q的充要条件.
2.且、或、非
p或q 记作p∨q p且q 记作p∧q 非p(命题的否定) 记作﹁ p
记忆:“同假为假” “同真为真” “真假相反”
(其余为真) (其余为假)
p q p或q
真 真 真
真 假 真
假 真 真
假 假 假
p q p且q
真 真 真
真 假 假
假 真 假
假 假 假
p 非p
真 假
假 真
3.四种命题
①若p为原命题条件,q为原命题结论.则:
原命题:若p则q 逆命题:若q则p
否命题:若﹁p则﹁q 逆否命题:若﹁q则﹁p
②四种命题关系:原命题与逆否命题,否命题与逆命题具有相同的真假性.
4.量词
①全称量词:“任意: ”;存在量词:“存在: ”.
②含有全称量词的命题称为全称命题;含有存在量词的命题称为特称命题.
③含有量词的命题的否定:
全称命题p: x∈M,p(x),它的否定﹁p: x0∈M,﹁p(x0)
存在性命题p: x0∈M,p(x0),它的否定﹁p: x∈M,﹁p(x)
1.设集合S={x|x2+2x=0,x∈R},T={x|x2-2x=0,x∈R},则S∩T=( )
A.{0} B.{0,2} C.{0,-2} D.{2,0,-2}
考点训练
【答案】 A
【解析】 ∵集合S={x|x2+2x=0}={0,-2},T={x|x2-2x=0}={0,2},
∴S∩T={0}.故选A.
【答案】 A
【解析】 ∵集合B={x|x=n2,n∈A}={1,4,9,16},
∴A∩B={1,4}.故选A.
2.已知集合A={1,2,3,4},B={x|x=n2,n∈A},则A∩B= ( )
A.{1,4} B.{2,3} C.{9,16} D.{1,2}
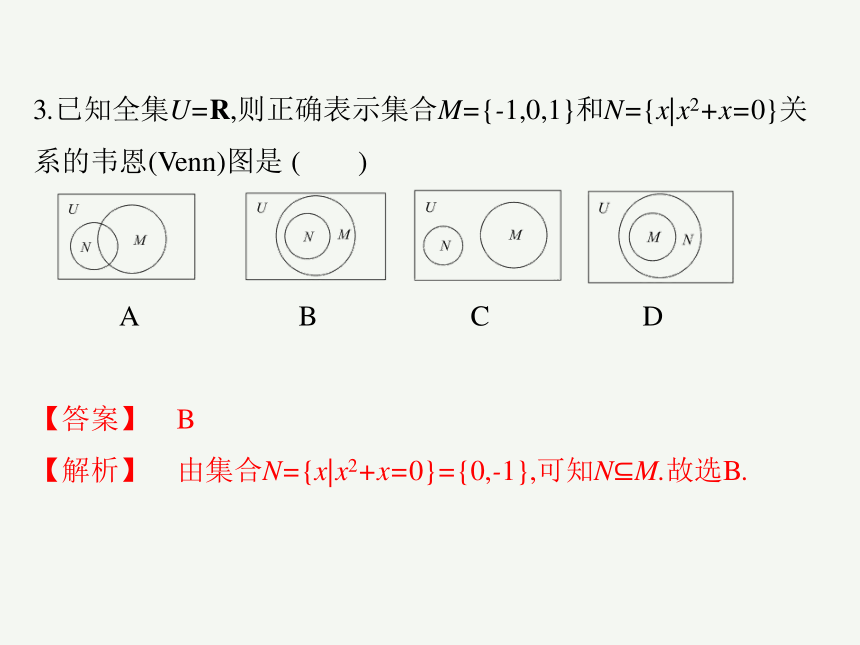
3.已知全集U=R,则正确表示集合M={-1,0,1}和N={x|x2+x=0}关系的韦恩(Venn)图是 ( )
A B C D
【答案】 B
【解析】 由集合N={x|x2+x=0}={0,-1},可知N M.故选B.
4.若集合A={0,1,2,3},B={1,2,4},则A∪B= ( )
A.{0,1,2,3,4} B.{1,2,3,4}
C.{1,2} D.{0}
【答案】 A
【解析】 集合A={0,1,2,3}与B={1,2,4},集合A与集合B的并集是{0,1,2,3,4}.故选A.
5.已知集合A={(x,y)|x,y为实数,且x2+y2=1},集合B={(x,y)|x,y为实数,且x+y=1},则A∩B的元素个数为 ( )
A.4 B.3 C.2 D.1
【答案】 C
【解析】 由题意可知,A∩B的元素个数即为圆x2+y2=1与直线x+y=1的交点的个数,如图可知圆与直线有两个交点.故选C.
本题也可以通过方程组的解的个数来确定.
6.已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},则A∩B中的元素个数为 ( )
A.5 B.4 C.3 D.2
【答案】 D
【解析】 由条件知,
当n=2时,3n+2=8;
当n=4时;3n+2=14.
故A∩B={8,14}.故选D.
7.集合U={1,2,3,4,5,6},S={1,4,5},T={2,3,4},则S∩( UT)等于( )
A.{1,4,5,6} B.{1,5}
C.{4} D.{1,2,3,4,5}
【答案】 B
【解析】 由题意得 UT={1,5,6},所以S∩( UT)={1,5}.故选B.
8.已知集合P={x|x2≤1},M={a},若P∪M=P,则a的取值范围是( )
A.(-∞,-1] B.[1,+∞)
C.[-1,1] D.(-∞,-1]∪[1,+∞)
【解析】 C
【解析】 化简得集合P={x|-1≤x≤1},又P∪M=P,所以M P,
所以-1≤a≤1.故选C.
9.集合A={0,2,a},B={1,a2},若A∪B={0,1,2,4,16},则a的值为( )
A.0 B.1 C.2 D.4
【答案】 D
【解析】 ∵集合A={0,2,a},B={1,a2},A∪B={0,1,2,4,16},
∴∴a=4.故选D.
10.设集合A={x|-3≤2x-1≤3},集合B为函数y=lg(x-1)的定义域,则A∩B= ( )
A.(1,2) B.[1,2] C.[1,2) D.(1,2]
【答案】 D
【解析】 因为集合A中x的取值范围是[-1,2],
而从集合B可以得出x∈(1,+∞).
所以集合A与B的交集是(1,2].故选D.
11.已知集合A={x|x2-x-2<0},B={x|-1A.A B B.B A C.A=B D.A∩B=
【答案】 B
【解析】 因为集合A={x|x2-x-2<0}={x|-112.已知集合A={x|-1A.(-1,3) B.(-1,0) C.(0,2) D.(2,3)
【答案】 A
【解析】 ∵集合A={x|-1∴A∪B={x|-113.已知集合M={x|lg x>0},N={x|x2≤4},则M∩N= ( )
A.(1,2) B.[1,2) C.(1,2] D.[1,2]
【答案】 C
【解析】 因为集合M={x|x>1},N={x|-2≤x≤2},
所以M∩N={x|114.已知集合A={x|x2-3x+2=0,x∈R},B={x|0A.1 B.2 C.3 D.4
【答案】 D
【解析】 因为集合A={1,2},B={1,2,3,4},
所以集合C可以是{1,2}{1,2,3}{1,2,4}{1,2,3,4}.故选D.
15.若集合A={x|2x-1>0},B={x},则A∩B= .
【答案】 {x|【解析】 因为集合A={x|x>},B={x|-1≤x≤1},
所以A∩B={x|16.集合A={x∈R||x-2|≤5}中的最小整数是 .
【答案】 -3
【解析】 因为集合A={x|-3≤x≤7},所以集合A中的最小整数是-3.
17.若集合M={x|-2A.M N B.M∩N={4}
C.M N D.M∪N={x|-2【答案】 B
【解析】 因为集合M={x|-2所以M∩N={4},M∪N={x|-2又M,N相互没有包含关系.故选B.
18.若集合M={x|<4},N={x|y=},则M∩N= ( )
A.{x|0≤x<2} B.{x|≤x<2}
C.{x|3≤x<16} D.{x|≤x<16}
【答案】 D
【解析】 ∵由<4,得0≤x<16,
则集合M={x|<4}={x|0≤x<16};
由3x-1≥0,得x≥,则集合N={x|3x≥1}={x|x≥}.
∴M∩N={x|0≤x<16}∩{x|x≥}={x|≤x<16}.故选D.
19.若集合A={x|x2≤1},B={x|<0},则A∩B= ( )
A.{x|0≤x<1} B.{x|0C.{x|-1≤x<1} D.{x|-1≤x≤1}
【答案】 B
【解析】 集合A={x|x2≤1}={x|-1≤x≤1},
B={x|<0}={x|0则A∩B={x|020.命题“ x∈R, n0∈N*,使得n0≥x2”的否定形式是 ( )
A. x∈R, n0∈N*,使得n0B. x∈R, n∈N*,使得nC. x0∈R, n0∈N*,使得n0<
D. x0∈R, n∈N*,使得n<
【答案】 D
【解析】 “ x∈R, n0∈N*,使得n0≥x2”的否定形式是“ x0∈R, n∈N*,使得n< ”.故选D.
21.“x>0”是“>0成立”的 ( )
A.充分非必要条件 B.必要非充分条件
C.非充分非必要条件 D.充要条件
【答案】 A
【解析】 显然当x>0时,>0成立,
但是,当x<0时,>0也成立,故反之不成立.
故选A.
22.命题“所有能被2整除的数都是偶数”的否定是 ( )
A.所有不能被2整除的数都是偶数
B.所有能被2整除的数都不是偶数
C.存在一个不能被2整除的数是偶数
D.存在一个能被2整除的数不是偶数
【答案】 D
【解析】 由于全称量词的否定是特称量词.故选D.
23.若a∈R,则“a=2”是“(a-1)(a-2)=0”的 ( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分又不必要条件
【答案】 A
【解析】 因为a=2 (a-1)(a-2)=0成立;
而(a-1)(a-2)=0时a=2或a=1,
于是(a-1)(a-2)=0时,a=2不一定成立.
所以“a=2”是“(a-1)(a-2)=0”的充分而不必要条件.故选A.
24.命题“存在实数x0,使x0>1”的否定是 ( )
A.对任意实数x,都有x>1 B.不存在实数x,使x≤1
C.对任意实数x,都有x≤1 D.存在实数x,使x≤1
【答案】 C
【解析】 命题“存在实数x0,使x0>1”的否定是“对任意实数x,都有x≤1”.故选C.
25.设x∈R,则“x>”是“2x2+x-1>0”的 ( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
【答案】 A
【解析】 2x2+x-1>0的解集为{x|x<-1或x>}.故选A.
26.(多选题)设全集U=R,集合A={y|y=x-2,x∈R},集合B={x|x2+x-2<0,x∈R},则 ( )
A.A∩B=(0,1) B.A∪B=(-2,+∞)
C.A∩( RB)=(0,+∞) D.A∪( RB)=R
【答案】 AB
【解析】 集合A={y|y>0},B={x|-2∴A∩B=(0,1),A∪B=(-2,+∞), RB={x|x≤-2或x≥1},
A∩( RB)=[1,+∞),A∪( RB)={x|x≤-2或x>0}≠R.故选AB.
27.(多选题)设集合M={x|x2+x-2≤0},N={x|log2x<1},若实数a∈(M∩N),则a的值可以是( )
A.1 B.-2 C.0.5 D.1.5
【答案】 AC
【解析】 集合M={x|-2≤x≤1},N={x|0∴M∩N={x|0又a∈(M∩N),
∴a的值可以是1或0.5.故选AC.
28.(多选题)已知集合A=[2,5),B=(a,+∞).若A B,则实数a的值可能是 ( )
A.-3 B.1 C.2 D.5
【答案】 AB
【解析】 ∵A B,∴a<2.故选AB.
29.(多选题)下列“若p,则q”形式的命题中,p是q的必要条件的是( )
A.若两直线的斜率相等,则两直线平行
B.若x>5,则x>10
C.若ac=bc,则a=b
D.若sin α=sin β,则α=β
【答案】 BCD
【解析】 A.两直线的斜率相等与两直线平行相互推不出.
B.若x>5,则x>10,pq,但q p.
C.若ac=bc,则a=b,pq,但q p.
D.若sin α=sin β,则α=β,pq,但q p.
∴只有B,C,D中p是q的必要条件.故选BCD.
30.(多选题)下列命题中的真命题是 ( )
A. x∈R,2x-1>0 B. x∈N*,(x-1)2>0
C. x0∈R,lg x0<1 D. x0∈R,tan x0=2
【答案】 ACD
【解析】 ∵指数函数y=2t的值域为(0,+∞),
∴任意x∈R,均可得到2x-1>0成立,故A项正确;
∵当x∈N*时,x-1∈N,可得(x-1)2≥0,当且仅当x=1时取等号,
∴存在x∈N*,使(x-1)2>0不成立,故B项不正确;
∵当x=1时,lg x=0<1,∴存在x0∈R,使得lg x0<1成立,故C项正确;
∵正切函数y=tan x的值域为R,∴存在x0,使得tan x0=2成立,故D项正确.故选ACD.
31.(多选题)若a,b,c∈R,则下列叙述中正确的是 ( )
A.“ab2>cb2”的充要条件是“a>c”
B.“a>1”是“<1”的充分不必要条件
C.“ax2+bx+c≥0对x∈R恒成立”的充要条件是“b2-4ac≤0”
D.“a<1”是“方程x2+x+a=0有一个正根和一个负根”的必要不充分条件
【答案】 BD
【解析】 对于A,ab2>cb2成立时,b2>0,所以a>c,即充分性成立;
a>c时,b2≥0,不能得出ab2>cb2,所以必要性不成立.
是充分不必要条件,故A错误.
【解析】 对于B,a>1时,<1成立,即充分性成立;
<1时,-1<0,解得a<0或a>1,即必要性不成立.
是充分不必要条件,故B正确.
对于C,ax2+bx+c≥0对x∈R恒成立时,或a=b=0,c≥0;
b2-4ac≤0时,不等式ax2+bx+c≥0对x∈R不恒成立.
是既不充分也不必要条件,故C错误.
对于D,a<1时,方程x2+x+a=0不一定有实数根,
如a=,Δ=1-4×=-1<0,方程无实根,所以充分性不成立;
方程x2+x+a=0有一个正根和一个负根时,a<0,所以a<1,必要性成立.
是必要不充分条件,故D正确.故选BD.
32.(多选题)下列四个条件中,能成为x>y的充分不必要条件的
是 ( )
A.xc2>yc2 B.<<0 C.|x|>|y| D.ln x>ln y
【答案】 ABD
【解析】 对于A,因为xc2>yc2,则c2≠0,则x>y,
反之x>y,当c=0时得不出xc2>yc2,
所以“xc2>yc2”是“x>y”的充分不必要条件,故A正确;
【解析】 对于B,因为由<<0可得yy,
但x>y不能推出<<0(因为x,y的正负不确定,比如x=1,y=-1),
所以“<<0”是“x>y”的充分不必要条件,故B正确;
对于C,因为由|x|>|y|可得x2>y2,则(x+y)(x-y)>0,不能推出x>y,
由x>y也不能推出|x|>|y|(如x=1,y=-2),
所以“|x|>|y|”是“x>y”的既不充分又不必要条件,故C错误;
对于D,因为ln x>ln y,则x>y,反之0>x>y,ln x,ln y无意义,得不出ln x>ln y,
所以“ln x>ln y”是“x>y”的充分不必要条件,故D正确.
故选ABD.
33.(多选题)若a>0,b>0,则使a>b成立的充要条件是 ( )
A.a2>b2 B.a2b>ab2 C.> D.a+>b+
【答案】 ABD
【解析】 当a>0,b>0时,a>b等价为a2>b2,故A是充要条件,正确;
∵a>b,ab>0,∴a2b>ab2成立,故B是充要条件,正确;
由>得ab+b>ab+a,即b>a,故C不是等价条件,错误;
若a>b>0,则<,则a+>b+成立,
反之,若a+>b+得a-b+-=(a-b)+=(a-b)>0,
即a-b>0,得a>b成立,故D是充要条件,正确.故选ABD.
34.(多选题)若 x0∈,使得2-λx0+1<0成立是假命题,则实数λ可能取值是 ( )
A. B.2 C.3 D.
【答案】 AB
【解析】 若 x0∈,使得2-λx0+1<0成立是假命题,
故对 x∈,2x2-λx+1≥0恒成立,
即2x+≥λ对任意的x∈恒成立,即≥λ.
因为2x+≥2,当且仅当x=时等号成立.
所以λ≤2.故选AB.
35.(多选题)“关于x的不等式x2-2ax+a>0对 x∈R恒成立”的一个必要不充分条件是 ( )
A.0【答案】 BD
【解析】 ∵关于x的不等式x2-2ax+a>0的解集为R,
∴函数f(x)=x2-2ax+a的图象始终在x轴上方,
即方程x2-2ax+a=0的Δ<0,
∴由(-2a)2-4a<0,解得0又∵{a|0∴“0≤a≤1”和“a≥0”是“关于x的不等式x2-2ax+a>0的解集为R”的必要不充分条件.故选BD.
专题一 集合与逻辑用语
【考试内容】 集合;子集;补集;交集;并集;逻辑联结词;四种命题;充分条件;必要条件
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 10 5 5 5 5 5 5
全国卷(乙卷) 5 5 5 5 5 10 5
新高考全国Ⅰ卷 5 5
新高考全国Ⅱ卷 5 5
重要考点回顾
一、常用符号及其含义
1.元素与集合的关系是:属于或不属于关系,用符号∈或 表示.
2.集合与集合的关系:用 , ,=表示;A是B的子集记为A B;
A是B的真子集记为A B.特别地:
①任何一个集合是它本身的子集,记为A A;
②空集是任何集合的子集,记为 A;空集是任何非空集合的真子集;
③如果A B,同时B A,那么A=B;如果A B,B C,那么A C.
④n个元素的集合子集有2n个;n个元素的集合真子集有2n-1个;
n个元素的集合非空真子集有2n-2个.
3.常用数集的符号
名称 非负整数集 (自然数集) 正整数集 整数集 有理数集 实数集
符号 N N*或N+ Z Q R
二、集合的运算
特别地,集合运算中常用到以下结论:
①A B A∩B=A;A B A∪B=B;A∩A=A;A∩ =
②A∪B A;A∪B B;A∪A=A;A∪ =A
③A∪( UA)=U; UU=
集合的并集 集合的交集 集合的补集
符号 表示 A∪B A∩B 若全集为U,则集合A的补集为 UA
图形 表示
意义 {x|x∈A或x∈B} {x|x∈A且x∈B} UA={x|x∈U且x A}
三、命题与简易逻辑
1.充要条件的判断:如果p q,则p是q的充分条件;
如果q p,则p是q的必要条件;
如果既有p q,又有q p,记作p q,则p是q的充要条件.
2.且、或、非
p或q 记作p∨q p且q 记作p∧q 非p(命题的否定) 记作﹁ p
记忆:“同假为假” “同真为真” “真假相反”
(其余为真) (其余为假)
p q p或q
真 真 真
真 假 真
假 真 真
假 假 假
p q p且q
真 真 真
真 假 假
假 真 假
假 假 假
p 非p
真 假
假 真
3.四种命题
①若p为原命题条件,q为原命题结论.则:
原命题:若p则q 逆命题:若q则p
否命题:若﹁p则﹁q 逆否命题:若﹁q则﹁p
②四种命题关系:原命题与逆否命题,否命题与逆命题具有相同的真假性.
4.量词
①全称量词:“任意: ”;存在量词:“存在: ”.
②含有全称量词的命题称为全称命题;含有存在量词的命题称为特称命题.
③含有量词的命题的否定:
全称命题p: x∈M,p(x),它的否定﹁p: x0∈M,﹁p(x0)
存在性命题p: x0∈M,p(x0),它的否定﹁p: x∈M,﹁p(x)
1.设集合S={x|x2+2x=0,x∈R},T={x|x2-2x=0,x∈R},则S∩T=( )
A.{0} B.{0,2} C.{0,-2} D.{2,0,-2}
考点训练
【答案】 A
【解析】 ∵集合S={x|x2+2x=0}={0,-2},T={x|x2-2x=0}={0,2},
∴S∩T={0}.故选A.
【答案】 A
【解析】 ∵集合B={x|x=n2,n∈A}={1,4,9,16},
∴A∩B={1,4}.故选A.
2.已知集合A={1,2,3,4},B={x|x=n2,n∈A},则A∩B= ( )
A.{1,4} B.{2,3} C.{9,16} D.{1,2}
3.已知全集U=R,则正确表示集合M={-1,0,1}和N={x|x2+x=0}关系的韦恩(Venn)图是 ( )
A B C D
【答案】 B
【解析】 由集合N={x|x2+x=0}={0,-1},可知N M.故选B.
4.若集合A={0,1,2,3},B={1,2,4},则A∪B= ( )
A.{0,1,2,3,4} B.{1,2,3,4}
C.{1,2} D.{0}
【答案】 A
【解析】 集合A={0,1,2,3}与B={1,2,4},集合A与集合B的并集是{0,1,2,3,4}.故选A.
5.已知集合A={(x,y)|x,y为实数,且x2+y2=1},集合B={(x,y)|x,y为实数,且x+y=1},则A∩B的元素个数为 ( )
A.4 B.3 C.2 D.1
【答案】 C
【解析】 由题意可知,A∩B的元素个数即为圆x2+y2=1与直线x+y=1的交点的个数,如图可知圆与直线有两个交点.故选C.
本题也可以通过方程组的解的个数来确定.
6.已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},则A∩B中的元素个数为 ( )
A.5 B.4 C.3 D.2
【答案】 D
【解析】 由条件知,
当n=2时,3n+2=8;
当n=4时;3n+2=14.
故A∩B={8,14}.故选D.
7.集合U={1,2,3,4,5,6},S={1,4,5},T={2,3,4},则S∩( UT)等于( )
A.{1,4,5,6} B.{1,5}
C.{4} D.{1,2,3,4,5}
【答案】 B
【解析】 由题意得 UT={1,5,6},所以S∩( UT)={1,5}.故选B.
8.已知集合P={x|x2≤1},M={a},若P∪M=P,则a的取值范围是( )
A.(-∞,-1] B.[1,+∞)
C.[-1,1] D.(-∞,-1]∪[1,+∞)
【解析】 C
【解析】 化简得集合P={x|-1≤x≤1},又P∪M=P,所以M P,
所以-1≤a≤1.故选C.
9.集合A={0,2,a},B={1,a2},若A∪B={0,1,2,4,16},则a的值为( )
A.0 B.1 C.2 D.4
【答案】 D
【解析】 ∵集合A={0,2,a},B={1,a2},A∪B={0,1,2,4,16},
∴∴a=4.故选D.
10.设集合A={x|-3≤2x-1≤3},集合B为函数y=lg(x-1)的定义域,则A∩B= ( )
A.(1,2) B.[1,2] C.[1,2) D.(1,2]
【答案】 D
【解析】 因为集合A中x的取值范围是[-1,2],
而从集合B可以得出x∈(1,+∞).
所以集合A与B的交集是(1,2].故选D.
11.已知集合A={x|x2-x-2<0},B={x|-1
【答案】 B
【解析】 因为集合A={x|x2-x-2<0}={x|-1
【答案】 A
【解析】 ∵集合A={x|-1
A.(1,2) B.[1,2) C.(1,2] D.[1,2]
【答案】 C
【解析】 因为集合M={x|x>1},N={x|-2≤x≤2},
所以M∩N={x|1
【答案】 D
【解析】 因为集合A={1,2},B={1,2,3,4},
所以集合C可以是{1,2}{1,2,3}{1,2,4}{1,2,3,4}.故选D.
15.若集合A={x|2x-1>0},B={x},则A∩B= .
【答案】 {x|
所以A∩B={x|
【答案】 -3
【解析】 因为集合A={x|-3≤x≤7},所以集合A中的最小整数是-3.
17.若集合M={x|-2
C.M N D.M∪N={x|-2
【解析】 因为集合M={x|-2
18.若集合M={x|<4},N={x|y=},则M∩N= ( )
A.{x|0≤x<2} B.{x|≤x<2}
C.{x|3≤x<16} D.{x|≤x<16}
【答案】 D
【解析】 ∵由<4,得0≤x<16,
则集合M={x|<4}={x|0≤x<16};
由3x-1≥0,得x≥,则集合N={x|3x≥1}={x|x≥}.
∴M∩N={x|0≤x<16}∩{x|x≥}={x|≤x<16}.故选D.
19.若集合A={x|x2≤1},B={x|<0},则A∩B= ( )
A.{x|0≤x<1} B.{x|0
【答案】 B
【解析】 集合A={x|x2≤1}={x|-1≤x≤1},
B={x|<0}={x|0
A. x∈R, n0∈N*,使得n0
D. x0∈R, n∈N*,使得n<
【答案】 D
【解析】 “ x∈R, n0∈N*,使得n0≥x2”的否定形式是“ x0∈R, n∈N*,使得n< ”.故选D.
21.“x>0”是“>0成立”的 ( )
A.充分非必要条件 B.必要非充分条件
C.非充分非必要条件 D.充要条件
【答案】 A
【解析】 显然当x>0时,>0成立,
但是,当x<0时,>0也成立,故反之不成立.
故选A.
22.命题“所有能被2整除的数都是偶数”的否定是 ( )
A.所有不能被2整除的数都是偶数
B.所有能被2整除的数都不是偶数
C.存在一个不能被2整除的数是偶数
D.存在一个能被2整除的数不是偶数
【答案】 D
【解析】 由于全称量词的否定是特称量词.故选D.
23.若a∈R,则“a=2”是“(a-1)(a-2)=0”的 ( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分又不必要条件
【答案】 A
【解析】 因为a=2 (a-1)(a-2)=0成立;
而(a-1)(a-2)=0时a=2或a=1,
于是(a-1)(a-2)=0时,a=2不一定成立.
所以“a=2”是“(a-1)(a-2)=0”的充分而不必要条件.故选A.
24.命题“存在实数x0,使x0>1”的否定是 ( )
A.对任意实数x,都有x>1 B.不存在实数x,使x≤1
C.对任意实数x,都有x≤1 D.存在实数x,使x≤1
【答案】 C
【解析】 命题“存在实数x0,使x0>1”的否定是“对任意实数x,都有x≤1”.故选C.
25.设x∈R,则“x>”是“2x2+x-1>0”的 ( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
【答案】 A
【解析】 2x2+x-1>0的解集为{x|x<-1或x>}.故选A.
26.(多选题)设全集U=R,集合A={y|y=x-2,x∈R},集合B={x|x2+x-2<0,x∈R},则 ( )
A.A∩B=(0,1) B.A∪B=(-2,+∞)
C.A∩( RB)=(0,+∞) D.A∪( RB)=R
【答案】 AB
【解析】 集合A={y|y>0},B={x|-2
A∩( RB)=[1,+∞),A∪( RB)={x|x≤-2或x>0}≠R.故选AB.
27.(多选题)设集合M={x|x2+x-2≤0},N={x|log2x<1},若实数a∈(M∩N),则a的值可以是( )
A.1 B.-2 C.0.5 D.1.5
【答案】 AC
【解析】 集合M={x|-2≤x≤1},N={x|0
∴a的值可以是1或0.5.故选AC.
28.(多选题)已知集合A=[2,5),B=(a,+∞).若A B,则实数a的值可能是 ( )
A.-3 B.1 C.2 D.5
【答案】 AB
【解析】 ∵A B,∴a<2.故选AB.
29.(多选题)下列“若p,则q”形式的命题中,p是q的必要条件的是( )
A.若两直线的斜率相等,则两直线平行
B.若x>5,则x>10
C.若ac=bc,则a=b
D.若sin α=sin β,则α=β
【答案】 BCD
【解析】 A.两直线的斜率相等与两直线平行相互推不出.
B.若x>5,则x>10,pq,但q p.
C.若ac=bc,则a=b,pq,但q p.
D.若sin α=sin β,则α=β,pq,但q p.
∴只有B,C,D中p是q的必要条件.故选BCD.
30.(多选题)下列命题中的真命题是 ( )
A. x∈R,2x-1>0 B. x∈N*,(x-1)2>0
C. x0∈R,lg x0<1 D. x0∈R,tan x0=2
【答案】 ACD
【解析】 ∵指数函数y=2t的值域为(0,+∞),
∴任意x∈R,均可得到2x-1>0成立,故A项正确;
∵当x∈N*时,x-1∈N,可得(x-1)2≥0,当且仅当x=1时取等号,
∴存在x∈N*,使(x-1)2>0不成立,故B项不正确;
∵当x=1时,lg x=0<1,∴存在x0∈R,使得lg x0<1成立,故C项正确;
∵正切函数y=tan x的值域为R,∴存在x0,使得tan x0=2成立,故D项正确.故选ACD.
31.(多选题)若a,b,c∈R,则下列叙述中正确的是 ( )
A.“ab2>cb2”的充要条件是“a>c”
B.“a>1”是“<1”的充分不必要条件
C.“ax2+bx+c≥0对x∈R恒成立”的充要条件是“b2-4ac≤0”
D.“a<1”是“方程x2+x+a=0有一个正根和一个负根”的必要不充分条件
【答案】 BD
【解析】 对于A,ab2>cb2成立时,b2>0,所以a>c,即充分性成立;
a>c时,b2≥0,不能得出ab2>cb2,所以必要性不成立.
是充分不必要条件,故A错误.
【解析】 对于B,a>1时,<1成立,即充分性成立;
<1时,-1<0,解得a<0或a>1,即必要性不成立.
是充分不必要条件,故B正确.
对于C,ax2+bx+c≥0对x∈R恒成立时,或a=b=0,c≥0;
b2-4ac≤0时,不等式ax2+bx+c≥0对x∈R不恒成立.
是既不充分也不必要条件,故C错误.
对于D,a<1时,方程x2+x+a=0不一定有实数根,
如a=,Δ=1-4×=-1<0,方程无实根,所以充分性不成立;
方程x2+x+a=0有一个正根和一个负根时,a<0,所以a<1,必要性成立.
是必要不充分条件,故D正确.故选BD.
32.(多选题)下列四个条件中,能成为x>y的充分不必要条件的
是 ( )
A.xc2>yc2 B.<<0 C.|x|>|y| D.ln x>ln y
【答案】 ABD
【解析】 对于A,因为xc2>yc2,则c2≠0,则x>y,
反之x>y,当c=0时得不出xc2>yc2,
所以“xc2>yc2”是“x>y”的充分不必要条件,故A正确;
【解析】 对于B,因为由<<0可得y
但x>y不能推出<<0(因为x,y的正负不确定,比如x=1,y=-1),
所以“<<0”是“x>y”的充分不必要条件,故B正确;
对于C,因为由|x|>|y|可得x2>y2,则(x+y)(x-y)>0,不能推出x>y,
由x>y也不能推出|x|>|y|(如x=1,y=-2),
所以“|x|>|y|”是“x>y”的既不充分又不必要条件,故C错误;
对于D,因为ln x>ln y,则x>y,反之0>x>y,ln x,ln y无意义,得不出ln x>ln y,
所以“ln x>ln y”是“x>y”的充分不必要条件,故D正确.
故选ABD.
33.(多选题)若a>0,b>0,则使a>b成立的充要条件是 ( )
A.a2>b2 B.a2b>ab2 C.> D.a+>b+
【答案】 ABD
【解析】 当a>0,b>0时,a>b等价为a2>b2,故A是充要条件,正确;
∵a>b,ab>0,∴a2b>ab2成立,故B是充要条件,正确;
由>得ab+b>ab+a,即b>a,故C不是等价条件,错误;
若a>b>0,则<,则a+>b+成立,
反之,若a+>b+得a-b+-=(a-b)+=(a-b)>0,
即a-b>0,得a>b成立,故D是充要条件,正确.故选ABD.
34.(多选题)若 x0∈,使得2-λx0+1<0成立是假命题,则实数λ可能取值是 ( )
A. B.2 C.3 D.
【答案】 AB
【解析】 若 x0∈,使得2-λx0+1<0成立是假命题,
故对 x∈,2x2-λx+1≥0恒成立,
即2x+≥λ对任意的x∈恒成立,即≥λ.
因为2x+≥2,当且仅当x=时等号成立.
所以λ≤2.故选AB.
35.(多选题)“关于x的不等式x2-2ax+a>0对 x∈R恒成立”的一个必要不充分条件是 ( )
A.0
【解析】 ∵关于x的不等式x2-2ax+a>0的解集为R,
∴函数f(x)=x2-2ax+a的图象始终在x轴上方,
即方程x2-2ax+a=0的Δ<0,
∴由(-2a)2-4a<0,解得0
同课章节目录
