2023年高考数学客观题专题五 立体几何 课件(共74张PPT)
文档属性
| 名称 | 2023年高考数学客观题专题五 立体几何 课件(共74张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 80.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 12:31:28 | ||
图片预览








文档简介
(共74张PPT)
专题五 立体几何
【考试内容】 空间几何体的三视图;空间几何体的表面积及体积;线与线、线与面、面与面之间的平行关系及垂直关系;点到平面的距离
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 10 10 10 10 10 10 15
全国卷(乙卷) 10 10 15 5 15 10 10
新高考全国Ⅰ卷 10 15
新高考全国Ⅱ卷 15 10
重要考点回顾
一、简单几何体的表面积和体积的计算公式
1.圆柱、圆锥、球、圆台的表面积(c是底面周长,l为母线长)
圆柱的侧面积S=cl=2πrl,表面积S=2πrl+2πr2=2πr(r+l);
圆锥的侧面积S= cl=πrl,表面积S=πr2+πrl=πr(r+l);
球的表面积S=4πR2.
圆台的表面积S圆台=π(r'2+r2+r'l+rl)(r',r分别为上、下底面半径,l为母线长).
2.简单几何体的体积
棱柱和圆柱的体积V=S底×h(S底为底面积,h为高);
棱锥和圆锥的体积V= S底×h(S底为底面积,h为高);
棱台的体积V棱台=h(S'++S)(S',S分别为上、下底面面积,h为高);
圆台的体积V圆台=πh(r'2+r'r+r2)(r',r分别为上、下底面半径,h为高);
球的体积V= πR3.
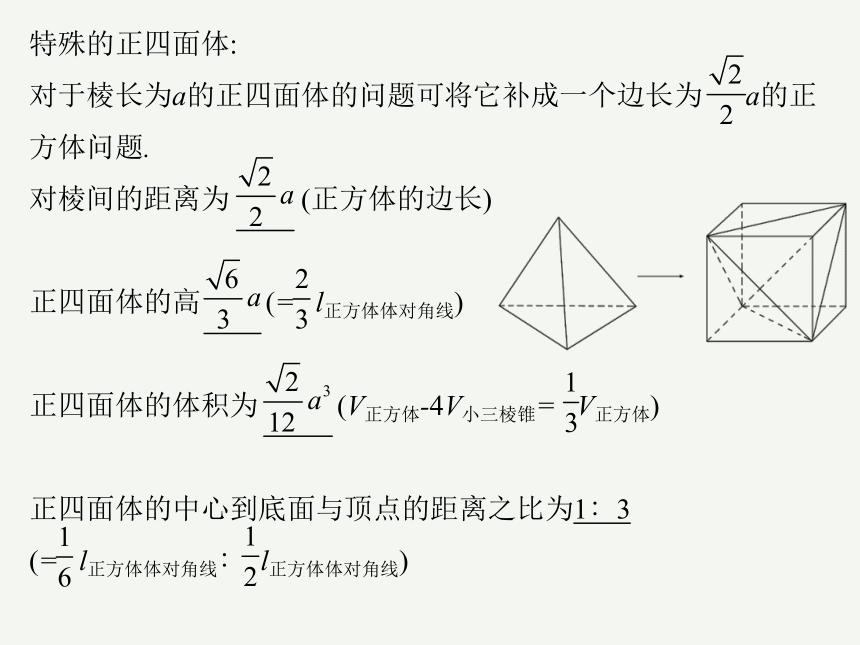
特殊的正四面体:
对于棱长为a的正四面体的问题可将它补成一个边长为 a的正方体问题.
对棱间的距离为 (正方体的边长)
正四面体的高 (= l正方体体对角线)
正四面体的体积为 (V正方体-4V小三棱锥= V正方体)
正四面体的中心到底面与顶点的距离之比为1∶3
(= l正方体体对角线∶ l正方体体对角线)
二、空间几何体的三视图和直观图
投影:把光由一点向外散射形成的投影叫中心投影,中心投影的投影线交于一点;
把在一束平行光线照射下的投影叫平行投影,平行投影的投影线是平行的.
正视图:光线从几何体的前面向后面正投影,得到的投影图.
侧视图:光线从几何体的左边向右边正投影,得到的投影图.
俯视图:光线从几何体的上面向下面正投影,得到的投影图.
★画三视图的原则:
正俯长相等、正侧高相同、俯侧宽一样
注:球的三视图都是圆;长方体的三视图都是矩形
三、点、直线、平面之间的位置关系
1.空间图形的公理
公理1 文字语言:如果一条直线的两点在一个平面内,那么这条直 线上的所有点都在这个平面内(即直线在平面内).
符号语言:A∈l,B∈l,A∈α,B∈α l α.
应用:证明或说明点在平面内,线在平面内.
公理2 文字语言:经过不在同一直线上的三点,有且只有一个平面 (即可以确定一个平面).
符号语言:若点C 直线AB,则点A、B、C确定一个平面α,又 可记作:平面ABC.
推论1 经过直线和直线外的一点,确定一个平面;
推论2 经过两相交直线,确定一个平面;
推论3 经过两平行直线,确定一个平面.
应用:证明点或线共面,确定平面.
公理3 文字语言:如果两个不重合的平面有一个公共点,那么它们 有且只有一条经过这个点的公共直线.
符号语言:A∈α∩β α∩β=a,A∈a.
应用:证明多点共线,多线共点,判定两平面相交.
公理4 文字语言:平行于同一直线的两条直线平行.
符号语言:a∥b,b∥c a∥c.
应用:证明线线平行.
2.直线、平面之间的位置关系
(1)空间两条直线
异面:没有公共点,不同在任何一个平面内
(2)空间角
①异面直线所成角:已知两条异面直线a,b,经过空间任一点O作直线a'∥a,b'∥b,我们把a',b'所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角).如果两条异面直线所成的角是直角,那么就说两条异面直线互相垂直.异面直线所成的角的范围为(0°,90°].
②直线与平面所成角:直线与平面斜交时,直线与其在平面内的射影所夹的锐角叫做直线与平面的夹角.直线与平面平行或在平面内时,直线与平面的夹角为0°.直线与平面垂直时,直线与平面的夹角为90°.直线与平面夹角的范围为[0°,90°].
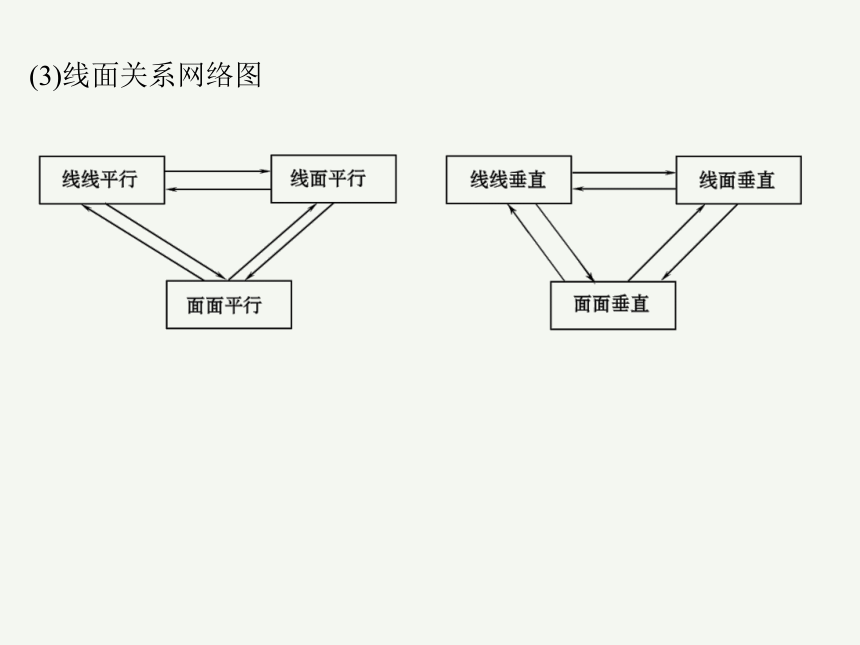
(3)线面关系网络图
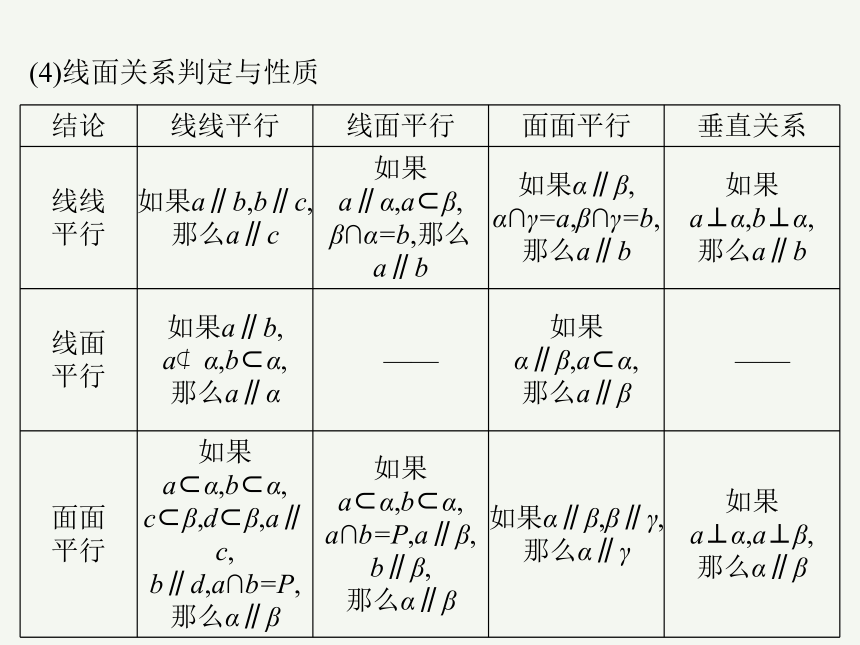
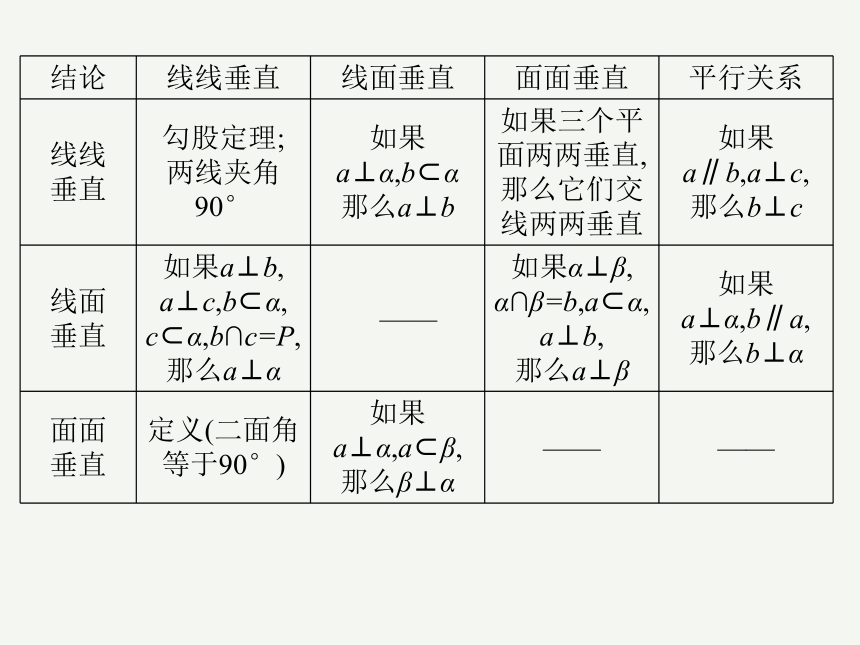
(4)线面关系判定与性质
结论 线线平行 线面平行 面面平行 垂直关系
线线 平行 如果a∥b,b∥c, 那么a∥c 如果a∥α,a β, β∩α=b,那么a∥b 如果α∥β, α∩γ=a,β∩γ=b, 那么a∥b 如果a⊥α,b⊥α,
那么a∥b
线面 平行 如果a∥b, a α,b α, 那么a∥α —— 如果α∥β,a α, 那么a∥β ——
面面 平行 如果a α,b α, c β,d β,a∥c, b∥d,a∩b=P, 那么α∥β 如果a α,b α, a∩b=P,a∥β, b∥β, 那么α∥β 如果α∥β,β∥γ, 那么α∥γ 如果a⊥α,a⊥β,
那么α∥β
结论 线线垂直 线面垂直 面面垂直 平行关系
线线 垂直 勾股定理; 两线夹角90° 如果a⊥α,b α 那么a⊥b 如果三个平面两两垂直,那么它们交线两两垂直 如果a∥b,a⊥c,
那么b⊥c
线面 垂直 如果a⊥b, a⊥c,b α, c α,b∩c=P,那么a⊥α —— 如果α⊥β, α∩β=b,a α, a⊥b, 那么a⊥β 如果a⊥α,b∥a,
那么b⊥α
面面 垂直 定义(二面角等于90°) 如果a⊥α,a β, 那么β⊥α —— ——
3.距离的求法
点点、点线、点面距离:点与点之间的距离就是两点之间线段的长;点与线、面间的距离是点到线、面垂足间线段的长.求它们首先要找到表示距离的线段,然后再计算.
注意:求点到面的距离的方法:
(1)直接法:直接确定点到平面的垂线段长;
(2)转移法:转化为另一点到该平面的距离(利用线面平行的性质);
(3)体积法:利用三棱锥体积公式.
(4)向量法:利用空间向量中点到平面的距离公式.
考点训练
1.一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是 ( )
A. B. C. D.
【答案】A
【解析】设圆柱底面的半径为r,则高为2πr,
全面积∶侧面积=[(2πr)2+2πr2]∶(2πr)2=.故选A.
2.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何 ”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少 ”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有 ( )
A.14斛 B.22斛 C.36斛 D.66斛
【答案】B
【解析】设圆锥的底面半径为r,则由r=8,解得r=,
故米堆的体积为××π××5≈.
∵1斛米的体积约为1.62立方尺,
∴÷1.62≈22(斛).故选B.
3.正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为,D为BC中点,则三棱锥A-B1DC1的体积为 ( )
A.3 B. C.1 D.
【答案】C
【解析】∵正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为,
D为BC中点,
∴底面B1DC1的面积为×2×=.
点A到底面B1DC1的距离就是底面正三角形的高h=.
则三棱锥A-B1DC1的体积为××=1.故选C.
4.已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为 ( )
A.2 B.2 C.4 D.4
【答案】B
【解析】由题意,设母线长为l.
因为圆锥底面周长即为侧面展开图半圆的弧长,圆锥的母线长即为侧面展开图半圆的半径,
则由2π·=π·l,解得l=2,所以该圆锥的母线长为2.故选B.
5.已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 ( )
A.12π B.12π C.8π D.10π
【答案】B
【解析】设圆柱的底面直径为2R,则高为2R,
圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,
可得4R2=8,解得R=.
则该圆柱的表面积为π×()2×2+2π×2=12π.故选B.
6.正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为 ( )
A.20+12 B.28 C. D.
【答案】D
【解析】如图,ABCD-A1B1C1D1为正四棱台,AB=2,A1B1=4,AA1=2.
在等腰梯形A1B1BA中,过A作AE⊥A1B1,可得A1E==1,
AE===.
连接AC,A1C1,则AC==2,A1C1==4,
过A作AG⊥A1C1,A1G==,AG===.
则正四棱台的体积为V=·h=×=.故选D.
6.正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为 ( )
A.20+12 B.28 C. D.
【答案】D
【解析】作出图形,连接该正四棱台上下底面的中心,如图.
∵该四棱台上下底面边长分别为2,4,侧棱长为2,
∴该棱台的高h==.
下底面面积S1=16,上底面面积S2=4,
则该棱台的体积为V=h(S1+S2+)=××(16+4+)=.故选D.
7.在长方体ABCD-A1B1C1D1中,AB=2,BC=1,直线AD与直线BC1所成的角为60°,则该长方体的体积为 ( )
A.2 B. C.2 D.
【答案】C
【解析】∵BC∥AD,直线AD与直线BC1所成的角为60°,
∴∠C1BC即为AD与BC1所成的角.
∴∠C1BC=60°,且BC=1,可得CC1=.
∴该长方体的体积V=2×1×=2.故选C.
8.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为 ( )
A. B.
C. D.
【答案】C
【解析】设正四棱锥的高为h,底面边长为a,侧面三角形底边上的高为h',
则依题意有因此有h'2-=ah',
即4-2-1=0,解得=(负值舍去).故选C.
9.设l,m,n表示直线,α,β表示平面,使“l⊥α”成立的充分条件是( )
A.α⊥β,l∥β B.α⊥β,l β
C.m α,n α,l⊥m,l⊥n D.l∥n,n⊥α
【答案】D
【解析】∵由l∥n,n⊥α,可得l⊥α,
∴“l∥n,n⊥α”是“l⊥α”的充分条件.
∴选项D满足题意,其他选项都不能推出l⊥α.
故选D.
10.已知两条直线m,n和平面α,则m⊥n的一个充分条件是 ( )
A.m⊥α且n⊥α B.m∥α且n α
C.m⊥α且n α D.m∥α且n∥α
【答案】 C
【解析】∵由m⊥α且n α,可推出m⊥n,
∴“m⊥α且n α”是“m⊥n”的一个充分条件.
而其他选项都不能推出m⊥n.故选C.
11.如图,在正方体ABCD-A1B1C1D1中,E,F分别为CC1,D1C1的中点,则下列直线中与直线BE相交的是 ( )
A.直线A1F B.直线AD1
C.直线C1D1 D.直线AA1
【答案】A
【解析】对于A,E,F分别为CC1,C1D1的中点,
所以EF∥CD1,即EF∥A1B,所以E,F,A1,B四点共面,
因为EF≠A1B,所以BE与A1F相交,故A正确;
对于B,因为AD1∥平面BCC1B1,BE 平面BCC1B1,
所以AD1与BE没有公共点,故B错误;
对于C,因为C1D1⊥平面BCC1B1,BE不过点C1,所以BE与C1D1异面,故C错误;
对于D,因为AA1∥平面BCC1B1,BE 平面BCC1B1,所以AA1与BE没有公共点,故D错误.故选A.
12.已知α,β是两个不同平面,l是空间中的直线,若l⊥α,则“l∥β”是“α⊥β”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】 A
【解析】∵命题“若l⊥α,l∥β,则α⊥β”为真命题;
若l⊥α,α⊥β,则l∥β或l β,
故命题“若l⊥α,α⊥β,则l∥β”为假命题,
∴若l⊥α,则“l∥β”是“α⊥β”的充分不必要条件.故选A.
13.如图,正方体ABCD-A1B1C1D1中,M是A1D的中点,则 ( )
A.直线MB与直线B1D1相交,直线MB 平面ABC1
B.直线MB与直线D1C平行,直线MB∥平面B1D1C
C.直线MB与直线A1D垂直,直线MB∥平面B1D1C
D.直线MB与直线AC异面,直线MB⊥平面ADC1B1
【答案】C
【解析】对于A,由于MB与BD相交,而BD与B1D1平行,
可得直线MB与直线B1D1异面,直线MB 平面ABC1,故A错误;
对于B,直线MB与A1B相交,而A1B与D1C平行,
所以MB与直线D1C异面,
平面A1BD与平面B1D1C平行,
可得直线MB与平面B1D1C平行,故B错误;
【解析】对于C,不妨设正方体的边长为1,则BD=,MD==.
因为AB⊥平面A1ADD1,AM 平面A1ADD1,所以AB⊥AM.
所以BM===.
所以BM2+MD2=BD2.所以BM⊥MD,即BM⊥A1D.
由上面的分析可得直线MB与平面B1D1C平行,故C正确;
对于D,由M不在平面ABC内,B不在直线AC上,
可得直线MB与直线AC异面.
若MB⊥平面ADC1B1,可得MB⊥AD,MB⊥B1C1.
而BC∥AD,可得MB⊥BC,进而得到MB⊥平面BCC1B1.
而AB⊥平面BCC1B1,所以MB与AB重合,矛盾,故D错误.
故选C.
14.如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则O到平面ABC1D1的距离为 ( )
A. B.
C. D.
【答案】B
【解析】过O作A1B1的平行线,交B1C1于E,
则O到平面ABC1D1的距离即为E到平面ABC1D1的距离.
作EF⊥BC1于F,易证EF⊥平面ABC1D1,
可求得EF=B1C=.故选B.
15.已知直二面角α-l-β,点A∈α,AC⊥l,C为垂足,B∈β,BD⊥l,D为垂足,若AB=2,AC=BD=1,则D到平面ABC的距离等于 ( )
A. B. C. D.1
【答案】C
【解析】由题意画出图形(如图所示).
直二面角α-l-β中,点A∈α,AC⊥l,C为垂足;B∈β,BD⊥l,D为垂足.
若AB=2,AC=BD=1,
则D到平面ABC的距离转化为三棱锥D-ABC的高为h.
所以AD=,CD=,BC=.
由VB-ACD=VD-ABC可知×AC·CD·BD=×AC·BC·h,解得h=.
故选C.
16.如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=2,PA=AB=1.则点D到平面PBC的距离为 ( )
A. B. C. D.
【答案】A
【解析】设点D到平面PBC的距离为h.
∵BC⊥AB,BC⊥PA,∴BC⊥平面PAB,∴BC⊥PB.
PB==,S△PBC=PB·BC=,S△BDC=BC·AB=1.
∴由VP-BDC=VD-PBC,即S△BDC·PA=S△PBC·h,解得h=.故选A.
17.如图,已知正方体ABCD-A1B1C1D1的棱长为1,则线段AD1上的动点P到直线A1C1的距离的最小值为 ( )
A.1 B. C. D.
【答案】D
【解析】线段AD1上的动点P到直线A1C1的距离的最小值等价于异面直线AD1,A1C1间的距离d.
因为A1C1与平面AD1C平行,故d等于A1到平面AD1C的距离,
由=可得,
××()2·d=××1×1×1,
解得d=.故选D.
18.在正方体ABCD-A1B1C1D1中,异面直线A1B与B1C所成的角
为 ( )
A.30° B.45° C.60° D.90°
【答案】 C
【解析】连接A1D,BD,则A1D∥B1C,
则异面直线A1B与B1C所成的角的平面角为∠BA1D(或其补角),
又A1D=BD=A1B,则∠BA1D=60°.故选C.
19.若正四面体A-BCD中,E,F分别为AB,DC的中点,则异面直线AF与CE所成角的余弦值为 ( )
A. B. C. D.
【答案】B
【解析】设AB=2,则AF=CE=,
又·=(+)·(+)
=(-2-·-·+·)
=×=-2,
设,所成角为θ,则cos θ==-,
即异面直线AF与CE所成角的余弦值为.故选B.
20.如图,在棱长为2的正方体ABCD-A1B1C1D1中,M,N,E,F分别是AD,DD1,BC,C1D1的中点,则异面直线MN与EF所成的角为( )
A. B. C. D.
【答案】C
【解析】取CC1的中点H,连接FH,EH.
由MN∥EH,则异面直线MN与EF所成的角的平面角为∠FEH(或其补角).
又AB=2,则EH=FH=,FE==,
则cos∠FEH==,则∠FEH=.故选C.
21.在三棱锥P-ABC中,PA⊥平面ABC,PA=AB,△ABC是正三角形,
M,N分别是AB,PC的中点,则直线MN,PB所成角的余弦值为( )
A. B. C. D.
【答案】D
【解析】取PA的中点E,AC的中点F.连接EN,NF.
由题意有EM∥PB,
则直线MN,PB所成角的平面角为∠EMN(或其补角).
设PA=2,
则EM=PB=,MN==,EN=1,
则cos∠EMN===,
即直线MN,PB所成角的余弦值为.故选D.
22.如图,在正四棱柱ABCD-A1B1C1D1中,底面边长为2,直线CC1与平面ACD1所成角的正弦值为,则正四棱柱的高为 ( )
A.2 B.3 C.4 D.5
【答案】C
【解析】以D为原点,以DA,DC,DD1为坐标轴建立空间坐标系(如图所示).设DD1=a,则A(2,0,0),C(0,2,0),D1(0,0,a),C1(0,2,a),
则=(-2,2,0),=(-2,0,a),=(0,0,a).
设平面ACD1的法向量为n=(x,y,z),
则即令x=1可得n=,
故cos===.
∵直线CC1与平面ACD1所成角的正弦值为,
∴由=,解得a=4.故选C.
23.正方体ABCD-A1B1C1D1中,AB1与平面ABC1D1所成的角为( )
A.30° B.45° C.60° D.90°
【答案】A
【解析】如图所示,建立空间直角坐标系.
不妨取AB=1,则D(0,0,0),A(1,0,0),B1(1,1,1),A1(1,0,1),则=(0,1,1).
取平面ABC1D1的法向量n==(1,0,1),
则直线AB1与平面ABC1D1所成的角的正弦值为|cos<,n>|===.
则直线AB1与平面ABC1D1所成的角为30°.故选A.
24.在所有棱长均相等的直三棱柱ABC-A1B1C1中,D,E分别为棱BB1,BC的中点,则直线A1B1与平面A1DE所成角的正弦值为( )
A. B. C. D.
【答案】B
【解析】如图所示,取AB的中点O,以O为原点,以OB,OC和平面ABC过点O的垂线为坐标轴建立空间直角坐标系.
设直三棱柱的棱长均为2,则A1(-1,0,2),D(1,0,1),E,
B1(1,0,2),则=(2,0,0),=(2,0,-1),=,
设平面A1DE的法向量为n=(x,y,z),
则即
令x=1得n=.
∵cos===,
∴直线A1B1与平面A1DE所成角的正弦值为|cos|=.故选B.
25.已知直四棱柱ABCD-A1B1C1D1的所有棱长相等,∠ABC=60°,则直线BC1与平面ABB1A1所成角的余弦值等于 ( )
A. B. C. D.
【答案】B
【解析】如图所示,取AB中点E,以A为原点,AE为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系.
设AB=2,则B(,-1,0),C1(,1,2),A(0,0,0),A1(0,0,2),=(0,2,2),
=(,-1,0),=(0,0,2).设平面ABB1A1的法向量为n=(x,y,z),
则取x=1,得n=(1,,0),
设直线BC1与平面ABB1A1所成角为θ,
则sin θ===.∵cos θ==.
∴直线BC1与平面ABB1A1所成角的余弦值等于.故选B.
26.如图,正方体ABCD-A1B1C1D1的棱AB和A1D1的中点分别为E,F,则直线EF与平面AA1D1D所成角的正弦值为 ( )
A. B. C. D.
【答案】C
【解析】如图所示,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系.
设正方体ABCD-A1B1C1D1的棱长为2,
则E(2,1,0),F(1,0,2),=(-1,-1,2).
平面AA1D1D的法向量n=(0,1,0),
设直线EF与平面AA1D1D所成角为θ,
则sin θ===.
则直线EF与平面AA1D1D所成角的正弦值为.故选C.
27.在正方体ABCD-A1B1C1D1中,E为棱CD上一点,且CE=2DE,F为棱AA1的中点,且平面BEF与DD1交于点G,则B1G与平面ABCD所成角的正切值为 ( )
A. B. C. D.
【答案】C
【解析】如图所示,以D为原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1的棱长为6.
∵E为棱CD上一点,且CE=2DE,F为棱AA1的中点,且平面BEF与DD1交于点G,
∴B1(6,6,6),G(0,0,1),=(-6,-6,-5),
平面ABCD的法向量n=(0,0,1),
设B1G与平面ABCD所成角为θ,
则sin θ==,可得tan θ=,
则B1G与平面ABCD所成角的正切值为.故选C.
28.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )
A.36π B.64π C.144π D.256π
【答案】C
【解析】如图所示,当点C位于垂直于平面AOB的直径端点时,三棱锥O-ABC的体积最大.
设球O的半径为R,
此时VO-ABC=VC-AOB=×·R2·R=R3=36,故R=6,
则球O的表面积为4πR2=144π.故选C.
29.已知底面边长为1,侧棱长为的正四棱柱的各顶点均在同一球面上,则该球的体积为 ( )
A. B.4π C.2π D.
【答案】 D
【解析】∵正四棱柱的底面边长为1,侧棱长为,
∴正四棱柱的体对角线的长为=2.
又∵正四棱柱的顶点在同一球面上,
∴正四棱柱的体对角线恰好是球的一条直径,得球的半径R=1.
根据球的体积公式,得该球的体积为V=πR3=.故选D.
30.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则该球的体积为 ( )
A.π B.4π C.4π D.6π
【答案】 B
【解析】因为平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,
所以球的半径为=.
所以球的体积为×()3=4π.故选B.
31.已知A,B,C为球O的球面上的三个点,☉O1为△ABC的外接圆.若☉O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为 ( )
A.64π B.48π C.36π D.32π
【答案】A
【解析】由题意可知图形如图所示.
由☉O1的面积为4π,可得O1A=2.
∵AO1=AB·sin 60°=AB,
∴AB=BC=AC=OO1=2.
∴球O的半径为R==4,
则球O的表面积为4×π×42=64π.故选A.
32.已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,
△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=
90°,则球O的体积为 ( )
A.8π B.4π C.2π D.π
【答案】D
【解析】如图,由PA=PB=PC,△ABC是边长为2的正三角形,可知三棱锥P-ABC为正三棱锥.则顶点P在底面的射影O1为底面三角形的中心,连接BO1并延长,交AC于G.
则AC⊥BG,又PO1⊥AC,PO1∩BG=O1,
可得AC⊥平面PBG,则PB⊥AC.
【解析】∵E,F分别是PA,AB的中点,∴EF∥PB.
又∠CEF=90°,即EF⊥CE,∴PB⊥CE,得PB⊥平面PAC.
则PB⊥PA,PB⊥PC,又三棱锥P-ABC是正三棱锥,
∴正三棱锥P-ABC的三条侧棱两两互相垂直.
把三棱锥补形为正方体,则正方体外接球即为三棱锥的外接球,
其直径为D=
=
===.
故半径为,则球O的体积为π×=π.故选D.
33.两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为,两个圆锥的高之比为1∶3,则这两个圆锥的体积之和为 ( )
A.3π B.4π C.9π D.12π
【答案】B
【解析】如图,设球O的半径为R,由题意,πR3=,
可得R=2,则球O的直径为4.
∵两个圆锥的高之比为1∶3,∴AO1=1,BO1=3.
由直角三角形中的射影定理可得r2=1×3,即r=.
∴这两个圆锥的体积之和为V=π×()2×(1+3)=4π.故选B.
34.已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为 .
π
【解析】因为圆锥内半径最大的球应该为该圆锥的内切球.
如图,圆锥母线BS=3,底面半径BC=1,
则其高SC==2.
不妨设该内切球与母线BS切于点D,
令OD=OC=r,由△SOD∽△SBC,则=,
即=,解得r=.
则球的体积为V=πr3=π.故答案为π.
35.已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为 .
【答案】36π
【解析】由题可知△SBC与△SAC都是等腰直角三角形,设球的半径为r.
可得×·2r·r·r=9,解得r=3.
则球O的表面积为4πr2=36π.
故答案为36π.
36.(多选题)在圆锥SO中,C是母线SA上靠近点S的三等分点,SA=l,底面圆的半径为r,圆锥SO的侧面积为3π,则 ( )
A.当l=3时,从点A到点C绕圆锥侧面一周的最小长度为
B.当r=时,过顶点S和两母线的截面三角形的最大面积为
C.当l=3时,圆锥SO的外接球表面积为
D.当l=3时,棱长为的正四面体在圆锥SO内可以任意转动
【答案】ACD
【解析】圆锥SO的侧面积为πrl=3π,则rl=3.
对于A,
当l=3时,r=1,将圆锥SO的侧面沿着母线SA展开如下图1所示,
则圆锥SO的底面周长为2π,∠ASC=,
在△SAC中,SA=3,SC=1,
由余弦定理可得
AC==,
故A正确;
【解析】对于B,
当r=时,l=2,设圆锥轴截面等腰三角形的顶角为α,
则cos α=<0,则α为钝角,
在圆O上任取两点M,N,则0<∠MSN≤α,
S△MSN=×22·sin∠MSN≤2,
当且仅当SM⊥SN时,等号成立,
故顶点和两母线的截面三角形的最大面积为2,故B错误;
【解析】对于C,
l=3时,r=1,此时外接球球心位于SO上,设为点M,
如图2,SO=2,SM=BM=R,
由勾股定理OM2+OB2=BM2,得(2-R)2+12=R2,解得R=,
则外接球表面积为4π×=,故C正确;
【解析】对于D,l=3时r=1,
如图3为圆锥底面和内接正三角形.
设三角形边长为a,
则a==>,
SO>,如图4,
故正四面体可在圆锥内放下并任意转动,故D正确.
故选ACD.
37.(多选题)在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足=λ+μ,其中λ∈[0,1],μ∈[0,1],则 ( )
A.当λ=1时,△AB1P的周长为定值
B.当μ=1时,三棱锥P-A1BC的体积为定值
C.当λ=时,有且仅有一个点P,使得A1P⊥BP
D.当μ=时,有且仅有一个点P,使得A1B⊥平面AB1P
【答案】BD
【解析】对于A,
当λ=1时,=+μ,即=μ,
所以∥,
故点P在线段CC1上(如图1),
此时△AB1P的周长为AB1+B1P+AP.
当点P为CC1的中点时,△AB1P的周长为+;
当点P在点C1处时,△AB1P的周长为2+1,
故周长不为定值,故A错误;
【解析】对于B,
当μ=1时,=λ+,即=λ,所以∥.
故点P在线段B1C1上(如图2).
因为B1C1∥平面A1BC,
所以直线B1C1上的点到平面A1BC的距离相等.
又△A1BC的面积为定值,
所以三棱锥P-A1BC的体积为定值,故B正确;
【解析】 对于C,
当λ=时,取线段BC,B1C1的中点分别为M,M1,连结M1M.
因为=+μ,即=μ,所以∥.
则点P在线段M1M上(如图3).
当点P在M1处时,A1M1⊥B1C1,A1M1⊥B1B,
又B1C1∩B1B=B1,
所以A1M1⊥平面BB1C1C.
又BM1 平面BB1C1C,
所以A1M1⊥BM1,即A1P⊥BP.
同理,当点P在M处,A1P⊥BP,故C错误;
【解析】对于D,当μ=时,取CC1的中点D1,BB1的中点D,
因为=λ+,即=λ,
所以∥.
则点P在线段DD1上(如图4).
当点P在点D1处时,取AC的中点E,连结A1E,BE.
因为BE⊥平面ACC1A1,又AD1 平面ACC1A1,所以AD1⊥BE.
在正方形ACC1A1中,AD1⊥A1E,又BE∩A1E=E,BE,A1E 平面A1BE,
故AD1⊥平面A1BE.又A1B 平面A1BE,所以A1B⊥AD1.
在正方形ABB1A1中,A1B⊥AB1,
又AD1∩AB1=A,AD1,AB1 平面AB1D1,所以A1B⊥平面AB1D1.
因为过定点A与定直线A1B垂直的平面有且只有一个,
故有且仅有一个点P,使得A1B⊥平面AB1P,故D正确. 故选BD.
38.(多选题)在所有棱长都相等的正三棱柱中,点A是三棱柱的顶点,M,N,Q是所在棱的中点,则下列选项中直线AQ与直线MN垂直的是 ( )
A B C D
【答案】AC
【解析】对于A,∵在底面内,AQ垂直于MN在
底面内的射影,∴AQ⊥MN.故A正确;
对于B,∵在底面内,MN不垂直于AQ在底面内的
射影MA,∴AQ不垂直MN.故B错误;
对于C,如图,在后侧面内,MN垂直于AQ在后侧面内的射影AP,
∴AQ⊥MN.故C正确;
对于D,∵在后侧面内,MN不垂直于AQ在后侧面内的射影MQ,
∴AQ不垂直MN.故D错误.
故选AC.
39.(多选题)如图,在正方体ABCD-A1B1C1D1中,E为AB的中点,则下列条件中,能使直线EF∥平面ACD1的有 ( )
A.F为AA1的中点
B.F为BB1的中点
C.F为CC1的中点
D.F为A1D1的中点
【答案】ACD
【解析】如图,M,G,H,I,J分别是棱BC,CC1,C1D1,D1A1,A1A的中点,易证E与M,G,H,I,J共面.
由EM∥AC,AC 平面ACD1,EM 平面ACD1,则EM∥平面ACD1,
同理EJ∥平面ACD1,而EM,EJ是平面EMGHIJ内相交直线,
则得平面EMGHIJ∥平面ACD1.
因为EF∥平面ACD1,
所以点F∈平面MGHIJ,
观察各选项,ACD满足.
故选ACD.
40.(多选题)如图,在直四棱柱ABCD-A1B1C1D1中,BC⊥CD,AB∥CD,
BC=,AA1=AB=AD=2,点P,Q,R分别在棱BB1,CC1,DD1上,若A,P,
Q,R四点共面,则下列结论正确的是 ( )
A.任意点P,都有AP∥QR
B.存在点P,使得四边形APQR为平行四边形
C.存在点P,使得BC∥平面APQR
D.存在点P,使得△APR为等腰直角三角形
【答案】AC
【解析】对于A,由直四棱柱ABCD-A1B1C1D1,AB∥CD,
所以平面ABB1A1∥平面DCC1D1.
又因为平面APQR∩平面ABB1A1=AP,
平面APQR∩平面DCC1D1=QR,
所以AP∥QR.故A正确;
对于B,若四边形APQR为平行四边形,则AR∥QP,
而AD与BC不平行,即平面ADD1A1与平面BCC1B1不平行,
所以平面APQR∩平面BCC1B1=PQ,平面APQR∩平面ADD1A1=AR,
直线PQ与直线AR不平行,与AR∥QP矛盾,
所以四边形APQR不可能是平行四边形.故B错误;
【解析】对于C,如图所示,延长CD至M,使得DM=CD,连接AM,MR,则四边形ABCM为矩形,所以BC∥AM.当R,Q,M三点共线时,
AM 平面APQR,此时BC∥平面APQR.故C正确;
对于D,假设存在点P,使得△APR为等腰直角三角形,令BP=x,
由AP===AR==,
所以BP=DR=x.且由BP∥DR,可知四边形BPDR为平行四边BPDR.
所以RP=BD=.
过点D作DE⊥AB,则DE=BC=,
所以AE=1,即CD=BE=1.
所以RP==2=AP=
=,无解.故D错误.
故选AC.
专题五 立体几何
【考试内容】 空间几何体的三视图;空间几何体的表面积及体积;线与线、线与面、面与面之间的平行关系及垂直关系;点到平面的距离
【近7年全国卷考点统计】
试卷类型 2016 2017 2018 2019 2020 2021 2022
全国卷(甲卷) 10 10 10 10 10 10 15
全国卷(乙卷) 10 10 15 5 15 10 10
新高考全国Ⅰ卷 10 15
新高考全国Ⅱ卷 15 10
重要考点回顾
一、简单几何体的表面积和体积的计算公式
1.圆柱、圆锥、球、圆台的表面积(c是底面周长,l为母线长)
圆柱的侧面积S=cl=2πrl,表面积S=2πrl+2πr2=2πr(r+l);
圆锥的侧面积S= cl=πrl,表面积S=πr2+πrl=πr(r+l);
球的表面积S=4πR2.
圆台的表面积S圆台=π(r'2+r2+r'l+rl)(r',r分别为上、下底面半径,l为母线长).
2.简单几何体的体积
棱柱和圆柱的体积V=S底×h(S底为底面积,h为高);
棱锥和圆锥的体积V= S底×h(S底为底面积,h为高);
棱台的体积V棱台=h(S'++S)(S',S分别为上、下底面面积,h为高);
圆台的体积V圆台=πh(r'2+r'r+r2)(r',r分别为上、下底面半径,h为高);
球的体积V= πR3.
特殊的正四面体:
对于棱长为a的正四面体的问题可将它补成一个边长为 a的正方体问题.
对棱间的距离为 (正方体的边长)
正四面体的高 (= l正方体体对角线)
正四面体的体积为 (V正方体-4V小三棱锥= V正方体)
正四面体的中心到底面与顶点的距离之比为1∶3
(= l正方体体对角线∶ l正方体体对角线)
二、空间几何体的三视图和直观图
投影:把光由一点向外散射形成的投影叫中心投影,中心投影的投影线交于一点;
把在一束平行光线照射下的投影叫平行投影,平行投影的投影线是平行的.
正视图:光线从几何体的前面向后面正投影,得到的投影图.
侧视图:光线从几何体的左边向右边正投影,得到的投影图.
俯视图:光线从几何体的上面向下面正投影,得到的投影图.
★画三视图的原则:
正俯长相等、正侧高相同、俯侧宽一样
注:球的三视图都是圆;长方体的三视图都是矩形
三、点、直线、平面之间的位置关系
1.空间图形的公理
公理1 文字语言:如果一条直线的两点在一个平面内,那么这条直 线上的所有点都在这个平面内(即直线在平面内).
符号语言:A∈l,B∈l,A∈α,B∈α l α.
应用:证明或说明点在平面内,线在平面内.
公理2 文字语言:经过不在同一直线上的三点,有且只有一个平面 (即可以确定一个平面).
符号语言:若点C 直线AB,则点A、B、C确定一个平面α,又 可记作:平面ABC.
推论1 经过直线和直线外的一点,确定一个平面;
推论2 经过两相交直线,确定一个平面;
推论3 经过两平行直线,确定一个平面.
应用:证明点或线共面,确定平面.
公理3 文字语言:如果两个不重合的平面有一个公共点,那么它们 有且只有一条经过这个点的公共直线.
符号语言:A∈α∩β α∩β=a,A∈a.
应用:证明多点共线,多线共点,判定两平面相交.
公理4 文字语言:平行于同一直线的两条直线平行.
符号语言:a∥b,b∥c a∥c.
应用:证明线线平行.
2.直线、平面之间的位置关系
(1)空间两条直线
异面:没有公共点,不同在任何一个平面内
(2)空间角
①异面直线所成角:已知两条异面直线a,b,经过空间任一点O作直线a'∥a,b'∥b,我们把a',b'所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角).如果两条异面直线所成的角是直角,那么就说两条异面直线互相垂直.异面直线所成的角的范围为(0°,90°].
②直线与平面所成角:直线与平面斜交时,直线与其在平面内的射影所夹的锐角叫做直线与平面的夹角.直线与平面平行或在平面内时,直线与平面的夹角为0°.直线与平面垂直时,直线与平面的夹角为90°.直线与平面夹角的范围为[0°,90°].
(3)线面关系网络图
(4)线面关系判定与性质
结论 线线平行 线面平行 面面平行 垂直关系
线线 平行 如果a∥b,b∥c, 那么a∥c 如果a∥α,a β, β∩α=b,那么a∥b 如果α∥β, α∩γ=a,β∩γ=b, 那么a∥b 如果a⊥α,b⊥α,
那么a∥b
线面 平行 如果a∥b, a α,b α, 那么a∥α —— 如果α∥β,a α, 那么a∥β ——
面面 平行 如果a α,b α, c β,d β,a∥c, b∥d,a∩b=P, 那么α∥β 如果a α,b α, a∩b=P,a∥β, b∥β, 那么α∥β 如果α∥β,β∥γ, 那么α∥γ 如果a⊥α,a⊥β,
那么α∥β
结论 线线垂直 线面垂直 面面垂直 平行关系
线线 垂直 勾股定理; 两线夹角90° 如果a⊥α,b α 那么a⊥b 如果三个平面两两垂直,那么它们交线两两垂直 如果a∥b,a⊥c,
那么b⊥c
线面 垂直 如果a⊥b, a⊥c,b α, c α,b∩c=P,那么a⊥α —— 如果α⊥β, α∩β=b,a α, a⊥b, 那么a⊥β 如果a⊥α,b∥a,
那么b⊥α
面面 垂直 定义(二面角等于90°) 如果a⊥α,a β, 那么β⊥α —— ——
3.距离的求法
点点、点线、点面距离:点与点之间的距离就是两点之间线段的长;点与线、面间的距离是点到线、面垂足间线段的长.求它们首先要找到表示距离的线段,然后再计算.
注意:求点到面的距离的方法:
(1)直接法:直接确定点到平面的垂线段长;
(2)转移法:转化为另一点到该平面的距离(利用线面平行的性质);
(3)体积法:利用三棱锥体积公式.
(4)向量法:利用空间向量中点到平面的距离公式.
考点训练
1.一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是 ( )
A. B. C. D.
【答案】A
【解析】设圆柱底面的半径为r,则高为2πr,
全面积∶侧面积=[(2πr)2+2πr2]∶(2πr)2=.故选A.
2.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何 ”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少 ”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有 ( )
A.14斛 B.22斛 C.36斛 D.66斛
【答案】B
【解析】设圆锥的底面半径为r,则由r=8,解得r=,
故米堆的体积为××π××5≈.
∵1斛米的体积约为1.62立方尺,
∴÷1.62≈22(斛).故选B.
3.正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为,D为BC中点,则三棱锥A-B1DC1的体积为 ( )
A.3 B. C.1 D.
【答案】C
【解析】∵正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为,
D为BC中点,
∴底面B1DC1的面积为×2×=.
点A到底面B1DC1的距离就是底面正三角形的高h=.
则三棱锥A-B1DC1的体积为××=1.故选C.
4.已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为 ( )
A.2 B.2 C.4 D.4
【答案】B
【解析】由题意,设母线长为l.
因为圆锥底面周长即为侧面展开图半圆的弧长,圆锥的母线长即为侧面展开图半圆的半径,
则由2π·=π·l,解得l=2,所以该圆锥的母线长为2.故选B.
5.已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 ( )
A.12π B.12π C.8π D.10π
【答案】B
【解析】设圆柱的底面直径为2R,则高为2R,
圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,
可得4R2=8,解得R=.
则该圆柱的表面积为π×()2×2+2π×2=12π.故选B.
6.正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为 ( )
A.20+12 B.28 C. D.
【答案】D
【解析】如图,ABCD-A1B1C1D1为正四棱台,AB=2,A1B1=4,AA1=2.
在等腰梯形A1B1BA中,过A作AE⊥A1B1,可得A1E==1,
AE===.
连接AC,A1C1,则AC==2,A1C1==4,
过A作AG⊥A1C1,A1G==,AG===.
则正四棱台的体积为V=·h=×=.故选D.
6.正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为 ( )
A.20+12 B.28 C. D.
【答案】D
【解析】作出图形,连接该正四棱台上下底面的中心,如图.
∵该四棱台上下底面边长分别为2,4,侧棱长为2,
∴该棱台的高h==.
下底面面积S1=16,上底面面积S2=4,
则该棱台的体积为V=h(S1+S2+)=××(16+4+)=.故选D.
7.在长方体ABCD-A1B1C1D1中,AB=2,BC=1,直线AD与直线BC1所成的角为60°,则该长方体的体积为 ( )
A.2 B. C.2 D.
【答案】C
【解析】∵BC∥AD,直线AD与直线BC1所成的角为60°,
∴∠C1BC即为AD与BC1所成的角.
∴∠C1BC=60°,且BC=1,可得CC1=.
∴该长方体的体积V=2×1×=2.故选C.
8.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为 ( )
A. B.
C. D.
【答案】C
【解析】设正四棱锥的高为h,底面边长为a,侧面三角形底边上的高为h',
则依题意有因此有h'2-=ah',
即4-2-1=0,解得=(负值舍去).故选C.
9.设l,m,n表示直线,α,β表示平面,使“l⊥α”成立的充分条件是( )
A.α⊥β,l∥β B.α⊥β,l β
C.m α,n α,l⊥m,l⊥n D.l∥n,n⊥α
【答案】D
【解析】∵由l∥n,n⊥α,可得l⊥α,
∴“l∥n,n⊥α”是“l⊥α”的充分条件.
∴选项D满足题意,其他选项都不能推出l⊥α.
故选D.
10.已知两条直线m,n和平面α,则m⊥n的一个充分条件是 ( )
A.m⊥α且n⊥α B.m∥α且n α
C.m⊥α且n α D.m∥α且n∥α
【答案】 C
【解析】∵由m⊥α且n α,可推出m⊥n,
∴“m⊥α且n α”是“m⊥n”的一个充分条件.
而其他选项都不能推出m⊥n.故选C.
11.如图,在正方体ABCD-A1B1C1D1中,E,F分别为CC1,D1C1的中点,则下列直线中与直线BE相交的是 ( )
A.直线A1F B.直线AD1
C.直线C1D1 D.直线AA1
【答案】A
【解析】对于A,E,F分别为CC1,C1D1的中点,
所以EF∥CD1,即EF∥A1B,所以E,F,A1,B四点共面,
因为EF≠A1B,所以BE与A1F相交,故A正确;
对于B,因为AD1∥平面BCC1B1,BE 平面BCC1B1,
所以AD1与BE没有公共点,故B错误;
对于C,因为C1D1⊥平面BCC1B1,BE不过点C1,所以BE与C1D1异面,故C错误;
对于D,因为AA1∥平面BCC1B1,BE 平面BCC1B1,所以AA1与BE没有公共点,故D错误.故选A.
12.已知α,β是两个不同平面,l是空间中的直线,若l⊥α,则“l∥β”是“α⊥β”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】 A
【解析】∵命题“若l⊥α,l∥β,则α⊥β”为真命题;
若l⊥α,α⊥β,则l∥β或l β,
故命题“若l⊥α,α⊥β,则l∥β”为假命题,
∴若l⊥α,则“l∥β”是“α⊥β”的充分不必要条件.故选A.
13.如图,正方体ABCD-A1B1C1D1中,M是A1D的中点,则 ( )
A.直线MB与直线B1D1相交,直线MB 平面ABC1
B.直线MB与直线D1C平行,直线MB∥平面B1D1C
C.直线MB与直线A1D垂直,直线MB∥平面B1D1C
D.直线MB与直线AC异面,直线MB⊥平面ADC1B1
【答案】C
【解析】对于A,由于MB与BD相交,而BD与B1D1平行,
可得直线MB与直线B1D1异面,直线MB 平面ABC1,故A错误;
对于B,直线MB与A1B相交,而A1B与D1C平行,
所以MB与直线D1C异面,
平面A1BD与平面B1D1C平行,
可得直线MB与平面B1D1C平行,故B错误;
【解析】对于C,不妨设正方体的边长为1,则BD=,MD==.
因为AB⊥平面A1ADD1,AM 平面A1ADD1,所以AB⊥AM.
所以BM===.
所以BM2+MD2=BD2.所以BM⊥MD,即BM⊥A1D.
由上面的分析可得直线MB与平面B1D1C平行,故C正确;
对于D,由M不在平面ABC内,B不在直线AC上,
可得直线MB与直线AC异面.
若MB⊥平面ADC1B1,可得MB⊥AD,MB⊥B1C1.
而BC∥AD,可得MB⊥BC,进而得到MB⊥平面BCC1B1.
而AB⊥平面BCC1B1,所以MB与AB重合,矛盾,故D错误.
故选C.
14.如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则O到平面ABC1D1的距离为 ( )
A. B.
C. D.
【答案】B
【解析】过O作A1B1的平行线,交B1C1于E,
则O到平面ABC1D1的距离即为E到平面ABC1D1的距离.
作EF⊥BC1于F,易证EF⊥平面ABC1D1,
可求得EF=B1C=.故选B.
15.已知直二面角α-l-β,点A∈α,AC⊥l,C为垂足,B∈β,BD⊥l,D为垂足,若AB=2,AC=BD=1,则D到平面ABC的距离等于 ( )
A. B. C. D.1
【答案】C
【解析】由题意画出图形(如图所示).
直二面角α-l-β中,点A∈α,AC⊥l,C为垂足;B∈β,BD⊥l,D为垂足.
若AB=2,AC=BD=1,
则D到平面ABC的距离转化为三棱锥D-ABC的高为h.
所以AD=,CD=,BC=.
由VB-ACD=VD-ABC可知×AC·CD·BD=×AC·BC·h,解得h=.
故选C.
16.如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=2,PA=AB=1.则点D到平面PBC的距离为 ( )
A. B. C. D.
【答案】A
【解析】设点D到平面PBC的距离为h.
∵BC⊥AB,BC⊥PA,∴BC⊥平面PAB,∴BC⊥PB.
PB==,S△PBC=PB·BC=,S△BDC=BC·AB=1.
∴由VP-BDC=VD-PBC,即S△BDC·PA=S△PBC·h,解得h=.故选A.
17.如图,已知正方体ABCD-A1B1C1D1的棱长为1,则线段AD1上的动点P到直线A1C1的距离的最小值为 ( )
A.1 B. C. D.
【答案】D
【解析】线段AD1上的动点P到直线A1C1的距离的最小值等价于异面直线AD1,A1C1间的距离d.
因为A1C1与平面AD1C平行,故d等于A1到平面AD1C的距离,
由=可得,
××()2·d=××1×1×1,
解得d=.故选D.
18.在正方体ABCD-A1B1C1D1中,异面直线A1B与B1C所成的角
为 ( )
A.30° B.45° C.60° D.90°
【答案】 C
【解析】连接A1D,BD,则A1D∥B1C,
则异面直线A1B与B1C所成的角的平面角为∠BA1D(或其补角),
又A1D=BD=A1B,则∠BA1D=60°.故选C.
19.若正四面体A-BCD中,E,F分别为AB,DC的中点,则异面直线AF与CE所成角的余弦值为 ( )
A. B. C. D.
【答案】B
【解析】设AB=2,则AF=CE=,
又·=(+)·(+)
=(-2-·-·+·)
=×=-2,
设,所成角为θ,则cos θ==-,
即异面直线AF与CE所成角的余弦值为.故选B.
20.如图,在棱长为2的正方体ABCD-A1B1C1D1中,M,N,E,F分别是AD,DD1,BC,C1D1的中点,则异面直线MN与EF所成的角为( )
A. B. C. D.
【答案】C
【解析】取CC1的中点H,连接FH,EH.
由MN∥EH,则异面直线MN与EF所成的角的平面角为∠FEH(或其补角).
又AB=2,则EH=FH=,FE==,
则cos∠FEH==,则∠FEH=.故选C.
21.在三棱锥P-ABC中,PA⊥平面ABC,PA=AB,△ABC是正三角形,
M,N分别是AB,PC的中点,则直线MN,PB所成角的余弦值为( )
A. B. C. D.
【答案】D
【解析】取PA的中点E,AC的中点F.连接EN,NF.
由题意有EM∥PB,
则直线MN,PB所成角的平面角为∠EMN(或其补角).
设PA=2,
则EM=PB=,MN==,EN=1,
则cos∠EMN===,
即直线MN,PB所成角的余弦值为.故选D.
22.如图,在正四棱柱ABCD-A1B1C1D1中,底面边长为2,直线CC1与平面ACD1所成角的正弦值为,则正四棱柱的高为 ( )
A.2 B.3 C.4 D.5
【答案】C
【解析】以D为原点,以DA,DC,DD1为坐标轴建立空间坐标系(如图所示).设DD1=a,则A(2,0,0),C(0,2,0),D1(0,0,a),C1(0,2,a),
则=(-2,2,0),=(-2,0,a),=(0,0,a).
设平面ACD1的法向量为n=(x,y,z),
则即令x=1可得n=,
故cos
∵直线CC1与平面ACD1所成角的正弦值为,
∴由=,解得a=4.故选C.
23.正方体ABCD-A1B1C1D1中,AB1与平面ABC1D1所成的角为( )
A.30° B.45° C.60° D.90°
【答案】A
【解析】如图所示,建立空间直角坐标系.
不妨取AB=1,则D(0,0,0),A(1,0,0),B1(1,1,1),A1(1,0,1),则=(0,1,1).
取平面ABC1D1的法向量n==(1,0,1),
则直线AB1与平面ABC1D1所成的角的正弦值为|cos<,n>|===.
则直线AB1与平面ABC1D1所成的角为30°.故选A.
24.在所有棱长均相等的直三棱柱ABC-A1B1C1中,D,E分别为棱BB1,BC的中点,则直线A1B1与平面A1DE所成角的正弦值为( )
A. B. C. D.
【答案】B
【解析】如图所示,取AB的中点O,以O为原点,以OB,OC和平面ABC过点O的垂线为坐标轴建立空间直角坐标系.
设直三棱柱的棱长均为2,则A1(-1,0,2),D(1,0,1),E,
B1(1,0,2),则=(2,0,0),=(2,0,-1),=,
设平面A1DE的法向量为n=(x,y,z),
则即
令x=1得n=.
∵cos
∴直线A1B1与平面A1DE所成角的正弦值为|cos
25.已知直四棱柱ABCD-A1B1C1D1的所有棱长相等,∠ABC=60°,则直线BC1与平面ABB1A1所成角的余弦值等于 ( )
A. B. C. D.
【答案】B
【解析】如图所示,取AB中点E,以A为原点,AE为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系.
设AB=2,则B(,-1,0),C1(,1,2),A(0,0,0),A1(0,0,2),=(0,2,2),
=(,-1,0),=(0,0,2).设平面ABB1A1的法向量为n=(x,y,z),
则取x=1,得n=(1,,0),
设直线BC1与平面ABB1A1所成角为θ,
则sin θ===.∵cos θ==.
∴直线BC1与平面ABB1A1所成角的余弦值等于.故选B.
26.如图,正方体ABCD-A1B1C1D1的棱AB和A1D1的中点分别为E,F,则直线EF与平面AA1D1D所成角的正弦值为 ( )
A. B. C. D.
【答案】C
【解析】如图所示,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系.
设正方体ABCD-A1B1C1D1的棱长为2,
则E(2,1,0),F(1,0,2),=(-1,-1,2).
平面AA1D1D的法向量n=(0,1,0),
设直线EF与平面AA1D1D所成角为θ,
则sin θ===.
则直线EF与平面AA1D1D所成角的正弦值为.故选C.
27.在正方体ABCD-A1B1C1D1中,E为棱CD上一点,且CE=2DE,F为棱AA1的中点,且平面BEF与DD1交于点G,则B1G与平面ABCD所成角的正切值为 ( )
A. B. C. D.
【答案】C
【解析】如图所示,以D为原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1的棱长为6.
∵E为棱CD上一点,且CE=2DE,F为棱AA1的中点,且平面BEF与DD1交于点G,
∴B1(6,6,6),G(0,0,1),=(-6,-6,-5),
平面ABCD的法向量n=(0,0,1),
设B1G与平面ABCD所成角为θ,
则sin θ==,可得tan θ=,
则B1G与平面ABCD所成角的正切值为.故选C.
28.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )
A.36π B.64π C.144π D.256π
【答案】C
【解析】如图所示,当点C位于垂直于平面AOB的直径端点时,三棱锥O-ABC的体积最大.
设球O的半径为R,
此时VO-ABC=VC-AOB=×·R2·R=R3=36,故R=6,
则球O的表面积为4πR2=144π.故选C.
29.已知底面边长为1,侧棱长为的正四棱柱的各顶点均在同一球面上,则该球的体积为 ( )
A. B.4π C.2π D.
【答案】 D
【解析】∵正四棱柱的底面边长为1,侧棱长为,
∴正四棱柱的体对角线的长为=2.
又∵正四棱柱的顶点在同一球面上,
∴正四棱柱的体对角线恰好是球的一条直径,得球的半径R=1.
根据球的体积公式,得该球的体积为V=πR3=.故选D.
30.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则该球的体积为 ( )
A.π B.4π C.4π D.6π
【答案】 B
【解析】因为平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,
所以球的半径为=.
所以球的体积为×()3=4π.故选B.
31.已知A,B,C为球O的球面上的三个点,☉O1为△ABC的外接圆.若☉O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为 ( )
A.64π B.48π C.36π D.32π
【答案】A
【解析】由题意可知图形如图所示.
由☉O1的面积为4π,可得O1A=2.
∵AO1=AB·sin 60°=AB,
∴AB=BC=AC=OO1=2.
∴球O的半径为R==4,
则球O的表面积为4×π×42=64π.故选A.
32.已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,
△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=
90°,则球O的体积为 ( )
A.8π B.4π C.2π D.π
【答案】D
【解析】如图,由PA=PB=PC,△ABC是边长为2的正三角形,可知三棱锥P-ABC为正三棱锥.则顶点P在底面的射影O1为底面三角形的中心,连接BO1并延长,交AC于G.
则AC⊥BG,又PO1⊥AC,PO1∩BG=O1,
可得AC⊥平面PBG,则PB⊥AC.
【解析】∵E,F分别是PA,AB的中点,∴EF∥PB.
又∠CEF=90°,即EF⊥CE,∴PB⊥CE,得PB⊥平面PAC.
则PB⊥PA,PB⊥PC,又三棱锥P-ABC是正三棱锥,
∴正三棱锥P-ABC的三条侧棱两两互相垂直.
把三棱锥补形为正方体,则正方体外接球即为三棱锥的外接球,
其直径为D=
=
===.
故半径为,则球O的体积为π×=π.故选D.
33.两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为,两个圆锥的高之比为1∶3,则这两个圆锥的体积之和为 ( )
A.3π B.4π C.9π D.12π
【答案】B
【解析】如图,设球O的半径为R,由题意,πR3=,
可得R=2,则球O的直径为4.
∵两个圆锥的高之比为1∶3,∴AO1=1,BO1=3.
由直角三角形中的射影定理可得r2=1×3,即r=.
∴这两个圆锥的体积之和为V=π×()2×(1+3)=4π.故选B.
34.已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为 .
π
【解析】因为圆锥内半径最大的球应该为该圆锥的内切球.
如图,圆锥母线BS=3,底面半径BC=1,
则其高SC==2.
不妨设该内切球与母线BS切于点D,
令OD=OC=r,由△SOD∽△SBC,则=,
即=,解得r=.
则球的体积为V=πr3=π.故答案为π.
35.已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为 .
【答案】36π
【解析】由题可知△SBC与△SAC都是等腰直角三角形,设球的半径为r.
可得×·2r·r·r=9,解得r=3.
则球O的表面积为4πr2=36π.
故答案为36π.
36.(多选题)在圆锥SO中,C是母线SA上靠近点S的三等分点,SA=l,底面圆的半径为r,圆锥SO的侧面积为3π,则 ( )
A.当l=3时,从点A到点C绕圆锥侧面一周的最小长度为
B.当r=时,过顶点S和两母线的截面三角形的最大面积为
C.当l=3时,圆锥SO的外接球表面积为
D.当l=3时,棱长为的正四面体在圆锥SO内可以任意转动
【答案】ACD
【解析】圆锥SO的侧面积为πrl=3π,则rl=3.
对于A,
当l=3时,r=1,将圆锥SO的侧面沿着母线SA展开如下图1所示,
则圆锥SO的底面周长为2π,∠ASC=,
在△SAC中,SA=3,SC=1,
由余弦定理可得
AC==,
故A正确;
【解析】对于B,
当r=时,l=2,设圆锥轴截面等腰三角形的顶角为α,
则cos α=<0,则α为钝角,
在圆O上任取两点M,N,则0<∠MSN≤α,
S△MSN=×22·sin∠MSN≤2,
当且仅当SM⊥SN时,等号成立,
故顶点和两母线的截面三角形的最大面积为2,故B错误;
【解析】对于C,
l=3时,r=1,此时外接球球心位于SO上,设为点M,
如图2,SO=2,SM=BM=R,
由勾股定理OM2+OB2=BM2,得(2-R)2+12=R2,解得R=,
则外接球表面积为4π×=,故C正确;
【解析】对于D,l=3时r=1,
如图3为圆锥底面和内接正三角形.
设三角形边长为a,
则a==>,
SO>,如图4,
故正四面体可在圆锥内放下并任意转动,故D正确.
故选ACD.
37.(多选题)在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足=λ+μ,其中λ∈[0,1],μ∈[0,1],则 ( )
A.当λ=1时,△AB1P的周长为定值
B.当μ=1时,三棱锥P-A1BC的体积为定值
C.当λ=时,有且仅有一个点P,使得A1P⊥BP
D.当μ=时,有且仅有一个点P,使得A1B⊥平面AB1P
【答案】BD
【解析】对于A,
当λ=1时,=+μ,即=μ,
所以∥,
故点P在线段CC1上(如图1),
此时△AB1P的周长为AB1+B1P+AP.
当点P为CC1的中点时,△AB1P的周长为+;
当点P在点C1处时,△AB1P的周长为2+1,
故周长不为定值,故A错误;
【解析】对于B,
当μ=1时,=λ+,即=λ,所以∥.
故点P在线段B1C1上(如图2).
因为B1C1∥平面A1BC,
所以直线B1C1上的点到平面A1BC的距离相等.
又△A1BC的面积为定值,
所以三棱锥P-A1BC的体积为定值,故B正确;
【解析】 对于C,
当λ=时,取线段BC,B1C1的中点分别为M,M1,连结M1M.
因为=+μ,即=μ,所以∥.
则点P在线段M1M上(如图3).
当点P在M1处时,A1M1⊥B1C1,A1M1⊥B1B,
又B1C1∩B1B=B1,
所以A1M1⊥平面BB1C1C.
又BM1 平面BB1C1C,
所以A1M1⊥BM1,即A1P⊥BP.
同理,当点P在M处,A1P⊥BP,故C错误;
【解析】对于D,当μ=时,取CC1的中点D1,BB1的中点D,
因为=λ+,即=λ,
所以∥.
则点P在线段DD1上(如图4).
当点P在点D1处时,取AC的中点E,连结A1E,BE.
因为BE⊥平面ACC1A1,又AD1 平面ACC1A1,所以AD1⊥BE.
在正方形ACC1A1中,AD1⊥A1E,又BE∩A1E=E,BE,A1E 平面A1BE,
故AD1⊥平面A1BE.又A1B 平面A1BE,所以A1B⊥AD1.
在正方形ABB1A1中,A1B⊥AB1,
又AD1∩AB1=A,AD1,AB1 平面AB1D1,所以A1B⊥平面AB1D1.
因为过定点A与定直线A1B垂直的平面有且只有一个,
故有且仅有一个点P,使得A1B⊥平面AB1P,故D正确. 故选BD.
38.(多选题)在所有棱长都相等的正三棱柱中,点A是三棱柱的顶点,M,N,Q是所在棱的中点,则下列选项中直线AQ与直线MN垂直的是 ( )
A B C D
【答案】AC
【解析】对于A,∵在底面内,AQ垂直于MN在
底面内的射影,∴AQ⊥MN.故A正确;
对于B,∵在底面内,MN不垂直于AQ在底面内的
射影MA,∴AQ不垂直MN.故B错误;
对于C,如图,在后侧面内,MN垂直于AQ在后侧面内的射影AP,
∴AQ⊥MN.故C正确;
对于D,∵在后侧面内,MN不垂直于AQ在后侧面内的射影MQ,
∴AQ不垂直MN.故D错误.
故选AC.
39.(多选题)如图,在正方体ABCD-A1B1C1D1中,E为AB的中点,则下列条件中,能使直线EF∥平面ACD1的有 ( )
A.F为AA1的中点
B.F为BB1的中点
C.F为CC1的中点
D.F为A1D1的中点
【答案】ACD
【解析】如图,M,G,H,I,J分别是棱BC,CC1,C1D1,D1A1,A1A的中点,易证E与M,G,H,I,J共面.
由EM∥AC,AC 平面ACD1,EM 平面ACD1,则EM∥平面ACD1,
同理EJ∥平面ACD1,而EM,EJ是平面EMGHIJ内相交直线,
则得平面EMGHIJ∥平面ACD1.
因为EF∥平面ACD1,
所以点F∈平面MGHIJ,
观察各选项,ACD满足.
故选ACD.
40.(多选题)如图,在直四棱柱ABCD-A1B1C1D1中,BC⊥CD,AB∥CD,
BC=,AA1=AB=AD=2,点P,Q,R分别在棱BB1,CC1,DD1上,若A,P,
Q,R四点共面,则下列结论正确的是 ( )
A.任意点P,都有AP∥QR
B.存在点P,使得四边形APQR为平行四边形
C.存在点P,使得BC∥平面APQR
D.存在点P,使得△APR为等腰直角三角形
【答案】AC
【解析】对于A,由直四棱柱ABCD-A1B1C1D1,AB∥CD,
所以平面ABB1A1∥平面DCC1D1.
又因为平面APQR∩平面ABB1A1=AP,
平面APQR∩平面DCC1D1=QR,
所以AP∥QR.故A正确;
对于B,若四边形APQR为平行四边形,则AR∥QP,
而AD与BC不平行,即平面ADD1A1与平面BCC1B1不平行,
所以平面APQR∩平面BCC1B1=PQ,平面APQR∩平面ADD1A1=AR,
直线PQ与直线AR不平行,与AR∥QP矛盾,
所以四边形APQR不可能是平行四边形.故B错误;
【解析】对于C,如图所示,延长CD至M,使得DM=CD,连接AM,MR,则四边形ABCM为矩形,所以BC∥AM.当R,Q,M三点共线时,
AM 平面APQR,此时BC∥平面APQR.故C正确;
对于D,假设存在点P,使得△APR为等腰直角三角形,令BP=x,
由AP===AR==,
所以BP=DR=x.且由BP∥DR,可知四边形BPDR为平行四边BPDR.
所以RP=BD=.
过点D作DE⊥AB,则DE=BC=,
所以AE=1,即CD=BE=1.
所以RP==2=AP=
=,无解.故D错误.
故选AC.
同课章节目录
