湖南省益阳市箴言中学2013-2014学年高一下学期第一次月考试题 数学
文档属性
| 名称 | 湖南省益阳市箴言中学2013-2014学年高一下学期第一次月考试题 数学 |  | |
| 格式 | zip | ||
| 文件大小 | 85.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-03 14:51:46 | ||
图片预览




文档简介
湖南省益阳市箴言中学2013-2014学年高一下学期第一次月考试题 数学
(时间:120分钟 总分:120分)
1.选择题:(4分x10小题=40分)
1.sin(-π)的值是 ( )
A. B.- C. D.-
2. 下列各式不能化简为的是 ( )
A. B.
C. D.
3. 要得到函数y=sin(2x-)的图象,只要将函数y=sin2x的图象 ( )
A.向左平行移动个单位 B.向左平行移动个单位
C.向右平行移动个单位 D.向右平行移动个单位
4. 将下列各式按大小顺序排列,其中正确的是 ( )
A.cos0C.cos0>cos>cos1>cos30° D.cos0>cos>cos30°>cos1
5. 若向量a,b,c满足a∥b且a⊥c,则c·(a+2b)= ( )
A.0 B.2 C.3 D.4
6. 已知tanθ=2,则sin2θ+sinθcosθ-2cos2θ等于 ( )
A.- B. C.- D.
7. 若向量a=(1,1),b=(1,-1),c=(-2,4),则c等于 ( )
A.-a+3b B.a-3b
C.3a-b D.-3a+b
8. 已知a、b均为单位向量,它们的夹角为60°,那么|a+ 3b| = ( )
A. B. C. D.4
9. 函数y=-cos2x+sinx的值域为 ( )
A.[-1,1] B.[-,-1]
C.[-,1] D.[-1,]
10. 方程sinx=x2的正实根个数为 ( )
A.2个 B.3个 C.4个 D.无数个
2.填空题:(4分x5小题=20分)
11. 若A点的坐标为(-2,-1),则B点的坐标为
12. 一个扇形的周长是6,该扇形的中心角是1弧度,该扇形的面积是_______
13.已知向量=,= ,若向量与平行,则k=______
14. 在水流速度为4的河流中,有一艘船正沿与水流垂直的方向以8的速度航
行,则船自身航行速度大小为____________。
15.我们定义:“ab”为向量a 与向量b的“外积”,若向量a 与向量b的夹角为θ,
它的长度规定为:| ab|=|a ||b|sinθ,现已知:| a|=4, |b|=3, a·b=-2,则:
| ab|=____________
三.解答题:(本大题共6小题.解答时应写出必要的文字说明、证明过程或演算步骤)
16.(本题满分8分)已知f(α)=.
(1)化简f(α);
(2)若α是第三象限角,且cos(α-)=,求f(α)的值.
17. (本题满分8分)已知,,且与夹角为120°求:
⑴;
⑵ 与的夹角。
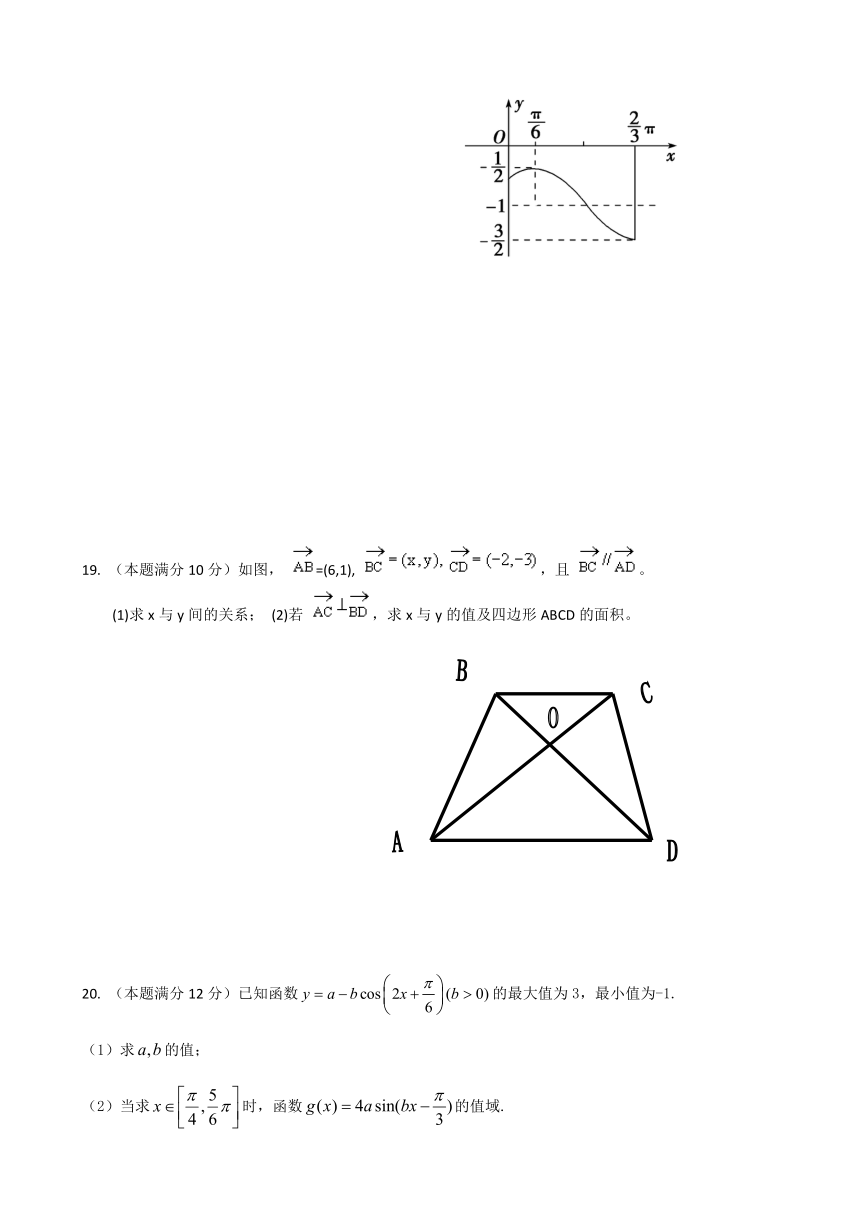
18. (本题满分10分)如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0,)的一段图象.
(1)写出此函数的解析式;
(2)求该函数的对称轴方程和对称中心坐标。
19. (本题满分10分)如图, =(6,1), ,且 。
(1)求x与y间的关系; (2)若 ,求x与y的值及四边形ABCD的面积。
20. (本题满分12分)已知函数的最大值为3,最小值为-1.
(1)求的值;
(2)当求时,函数的值域.
21. (本题满分12分)已知二次函数f(x) 的对称轴方程为:x=1,设向量a=(sinx,2), b=(2sinx,),c=( ,1),d=(2,1)。
(1)分别求a·b和c·d的取值范围;
(2)当x∈[0,π]时,求不等式f(a·b)>f(c·d)的解集。
益阳市箴言中学2014年上学期第一次月考试卷
座位号
高一数学 答题卷
(时间:120分钟 总分:120分)
1.选择题:(4分x10小题=40分)
题号 1 2 3 4 5 6 7 8 9 10
答案
2.填空题:(4分x5小题=20分)
11. 12.
13. 14.
15.
三.解答题:(本大题共6小题.解答时应写出必要的文字说明、证明过程或演算步骤.)
16.(本题共8分)
17.(本题共8分)
(本题共10分)
(本题共10分)
20.(本题共12分)
21.(本题共12分)
益阳市箴言中学2014年上学期第一次月考试卷
高一数学 参考答案
一.选择题:(4分x10小题=40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C D D A D B C C B
二.填空题:(4分x5小题=20分)
11. (1,3) 12. 2
13. 14.
15. 2
三.解答题:(本大题共6小题.解答时应写出必要的文字说明、证明过程或演算步骤)
16.解:(1)原式===-cosα.
(2)∵cos(α-)=-sinα,∴sinα=-,
又α是第三象限角,∴cosα=-=-=-,
∴f(α)=-cosα=.
17.解:由题意可得,,
(1);
(2)设与的夹角为,则,
又,所以,与的夹角为。
18.解:(1).y=sin(2x+)-1.
(2).对称轴方程:x=+,kZ
对称中心坐标:(-+,-1),kZ
19.解:(1)∵ ,
∴ 由 ,得x(y-2)=y(4+x), x+2y=0.
(2) 由 =(6+x, 1+y), 。
∵ , ∴(6+x)(x-2)+(1+y)(y-3)=0,
又x+2y=0, ∴ 或
∴当 时, , 当 时, 。
故 同向,
20.解:(1).a=1,b=2
(2)函数的值域为:
21.解:(1)a·b=2sin2x+11 c·d=2cos2x+11
(2.f(x)图象关于x=1对称
当二次项系数m>0时, f(x)在(1,)内单调递增,
由f(a·b)>f(c·d) a·b > c·d, 即2sin2x+1>2cos2x+1
又∵x∈[0,π] ∴x∈
当二次项系数m<0时,f(x)在(1,)内单调递减,
由f(a·b)>f(c·d) a·b > c·d, 即2sin2x+1<2cos2x+1
又∵x∈[0,π] ∴x∈
综上,当m>0时不等式的解集为;当m<0时不等式的解集为
班级 姓名 考号
(时间:120分钟 总分:120分)
1.选择题:(4分x10小题=40分)
1.sin(-π)的值是 ( )
A. B.- C. D.-
2. 下列各式不能化简为的是 ( )
A. B.
C. D.
3. 要得到函数y=sin(2x-)的图象,只要将函数y=sin2x的图象 ( )
A.向左平行移动个单位 B.向左平行移动个单位
C.向右平行移动个单位 D.向右平行移动个单位
4. 将下列各式按大小顺序排列,其中正确的是 ( )
A.cos0
5. 若向量a,b,c满足a∥b且a⊥c,则c·(a+2b)= ( )
A.0 B.2 C.3 D.4
6. 已知tanθ=2,则sin2θ+sinθcosθ-2cos2θ等于 ( )
A.- B. C.- D.
7. 若向量a=(1,1),b=(1,-1),c=(-2,4),则c等于 ( )
A.-a+3b B.a-3b
C.3a-b D.-3a+b
8. 已知a、b均为单位向量,它们的夹角为60°,那么|a+ 3b| = ( )
A. B. C. D.4
9. 函数y=-cos2x+sinx的值域为 ( )
A.[-1,1] B.[-,-1]
C.[-,1] D.[-1,]
10. 方程sinx=x2的正实根个数为 ( )
A.2个 B.3个 C.4个 D.无数个
2.填空题:(4分x5小题=20分)
11. 若A点的坐标为(-2,-1),则B点的坐标为
12. 一个扇形的周长是6,该扇形的中心角是1弧度,该扇形的面积是_______
13.已知向量=,= ,若向量与平行,则k=______
14. 在水流速度为4的河流中,有一艘船正沿与水流垂直的方向以8的速度航
行,则船自身航行速度大小为____________。
15.我们定义:“ab”为向量a 与向量b的“外积”,若向量a 与向量b的夹角为θ,
它的长度规定为:| ab|=|a ||b|sinθ,现已知:| a|=4, |b|=3, a·b=-2,则:
| ab|=____________
三.解答题:(本大题共6小题.解答时应写出必要的文字说明、证明过程或演算步骤)
16.(本题满分8分)已知f(α)=.
(1)化简f(α);
(2)若α是第三象限角,且cos(α-)=,求f(α)的值.
17. (本题满分8分)已知,,且与夹角为120°求:
⑴;
⑵ 与的夹角。
18. (本题满分10分)如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0,)的一段图象.
(1)写出此函数的解析式;
(2)求该函数的对称轴方程和对称中心坐标。
19. (本题满分10分)如图, =(6,1), ,且 。
(1)求x与y间的关系; (2)若 ,求x与y的值及四边形ABCD的面积。
20. (本题满分12分)已知函数的最大值为3,最小值为-1.
(1)求的值;
(2)当求时,函数的值域.
21. (本题满分12分)已知二次函数f(x) 的对称轴方程为:x=1,设向量a=(sinx,2), b=(2sinx,),c=( ,1),d=(2,1)。
(1)分别求a·b和c·d的取值范围;
(2)当x∈[0,π]时,求不等式f(a·b)>f(c·d)的解集。
益阳市箴言中学2014年上学期第一次月考试卷
座位号
高一数学 答题卷
(时间:120分钟 总分:120分)
1.选择题:(4分x10小题=40分)
题号 1 2 3 4 5 6 7 8 9 10
答案
2.填空题:(4分x5小题=20分)
11. 12.
13. 14.
15.
三.解答题:(本大题共6小题.解答时应写出必要的文字说明、证明过程或演算步骤.)
16.(本题共8分)
17.(本题共8分)
(本题共10分)
(本题共10分)
20.(本题共12分)
21.(本题共12分)
益阳市箴言中学2014年上学期第一次月考试卷
高一数学 参考答案
一.选择题:(4分x10小题=40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C D D A D B C C B
二.填空题:(4分x5小题=20分)
11. (1,3) 12. 2
13. 14.
15. 2
三.解答题:(本大题共6小题.解答时应写出必要的文字说明、证明过程或演算步骤)
16.解:(1)原式===-cosα.
(2)∵cos(α-)=-sinα,∴sinα=-,
又α是第三象限角,∴cosα=-=-=-,
∴f(α)=-cosα=.
17.解:由题意可得,,
(1);
(2)设与的夹角为,则,
又,所以,与的夹角为。
18.解:(1).y=sin(2x+)-1.
(2).对称轴方程:x=+,kZ
对称中心坐标:(-+,-1),kZ
19.解:(1)∵ ,
∴ 由 ,得x(y-2)=y(4+x), x+2y=0.
(2) 由 =(6+x, 1+y), 。
∵ , ∴(6+x)(x-2)+(1+y)(y-3)=0,
又x+2y=0, ∴ 或
∴当 时, , 当 时, 。
故 同向,
20.解:(1).a=1,b=2
(2)函数的值域为:
21.解:(1)a·b=2sin2x+11 c·d=2cos2x+11
(2.f(x)图象关于x=1对称
当二次项系数m>0时, f(x)在(1,)内单调递增,
由f(a·b)>f(c·d) a·b > c·d, 即2sin2x+1>2cos2x+1
又∵x∈[0,π] ∴x∈
当二次项系数m<0时,f(x)在(1,)内单调递减,
由f(a·b)>f(c·d) a·b > c·d, 即2sin2x+1<2cos2x+1
又∵x∈[0,π] ∴x∈
综上,当m>0时不等式的解集为;当m<0时不等式的解集为
班级 姓名 考号
同课章节目录
