第一章 直角三角形的边角关系单元检测试卷A(含答案)
文档属性
| 名称 | 第一章 直角三角形的边角关系单元检测试卷A(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 19:37:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版2022-20203年九年级(下)第一章直角三角形的边角检测试卷A
(时间120分钟,满分120分)
一、(共12小题;每小题3分,共36分)
1. 在 中,,,,那么 等于
A. B. C. D.
2. 如图,某河堤横断面迎水坡 的坡比是 ,堤高 的长为 米,则迎水坡的宽度 的长为
A. 米 B. 米 C. 米 D. 米
3. 如图,在 中,,, 分别是斜边 上的高和中线,下列结论不一定成立的是
A. B.
C. D.
4. 在 中,,那么 等于
A. B. C. D.
5. 如图,在四边形 中,,,,,则
A. B. C. D.
6. 在 中,,,则 的值为
A. B. C. D.
7. 如图, 中,, 在 轴上, 在 轴上,点 , 的坐标分别为 ,,把 沿着 对折得到 ,则点 的坐标为
A. B. C. D.
8. 国家近年来实施了新一轮农村电网改造升级工程,解决了农村供电“最后 公里”问题,电力公司在改造时把某一输电线铁塔建在了一个坡度为 的山坡 的平台 上(如图),测得 , 米, 米, 米,则铁塔 的高度约为(参考数据:,)
A. 米 B. 米 C. 米 D. 米
9. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:
()在点 处放置测角仪,测得旗杆顶的仰角 ;
()量得测角仪的高度 ;
()量得测角仪到旗杆的水平距离 .
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为
A. B. C. D.
10. 在 中,,.下列线段 的长度不能使 的形状和大小都确定的是
A. B. C. D.
11. 如图,在 中,,,,若用科学计算器求 的长,则下列按键顺序正确的是
A. B.
C. D.
12. 如图,垂直于水平面的 信号塔 建在垂直于水平面的悬崖边 点处,某测量员从山脚 点出发沿水平方向前行 米到 点(点 ,, 在同一直线上),再沿斜坡 方向前行 米到 点(点 ,,,, 在同一平面内),在点 处测得 信号塔顶端 的仰角为 ,悬崖 的高为 米,斜坡 的坡度(或坡比),则信号塔 的高度约为
(参考数据:,,)
A. 米 B. 米 C. 米 D. 米
二、(共6小题;每小题4分,共24分)
13. 在 中,若 ,则 的度数是 .
14. .(结果精确到 )
15. 在平面直角坐标系 中,已知点 的坐标为 ,那么直线 与 轴夹角的正切值是 .
16. 若 ,则锐角 .
17. 如图,如果小华沿坡度为 的坡面由 到 行走了 米,那么他实际上升的高度为 米.
18. 定义:有一组对边相等而另一组对边不相等的凸四边形叫做“对等四边形”,如图,在 中,,点 在边 上,点 在边 上,如果 ,,,四边形 为“对等四边形”,那么 的长为 .
三、(共7小题;共60分)
19.(12分)探究规律:
(1)应用计算器算一算.分别比较各个三角函数值的大小,并说一说有什么规律.(精确到 )
() ; ;
; .
规律: .
() ; ;
; .
规律: .
() ; ;
; .
规律: .
(2)拓展应用:
应用上面的规律比较大小.
① ,,,;
② ,,,.
20. (4分)计算:.
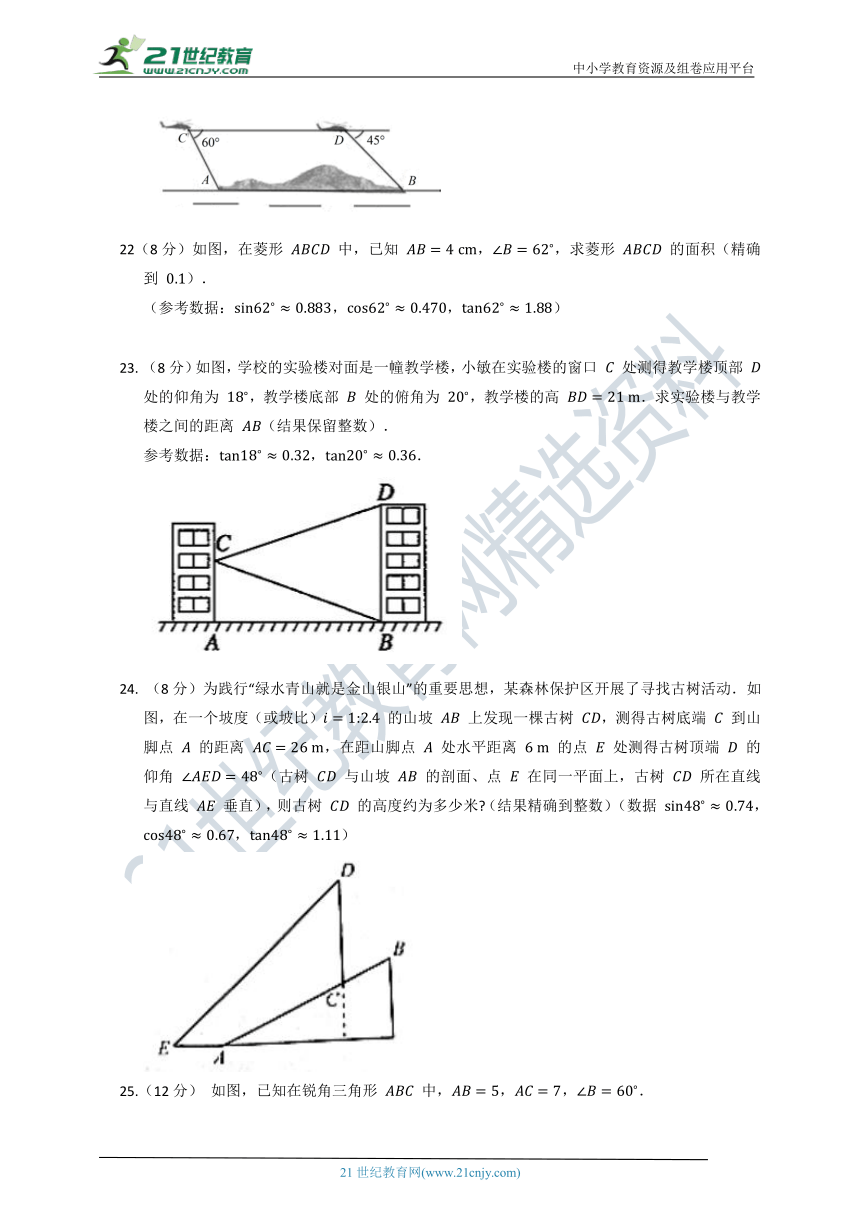
21. (8分)如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端 、 的距离,飞机以距海平面垂直同一高度飞行,在点 处测得端点 的俯角为 ,然后沿着平行于 的方向水平飞行了 米,在点 测得端点 的俯角为 ,已知岛屿两端 、 的距离 米,求飞机飞行的高度.(结果精确到 米,参考数据:,)
22(8分)如图,在菱形 中,已知 ,,求菱形 的面积(精确到 ).
(参考数据:,,)
23. (8分)如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口 处测得教学楼顶部 处的仰角为 ,教学楼底部 处的俯角为 ,教学楼的高 .求实验楼与教学楼之间的距离 (结果保留整数).
参考数据:,.
24. (8分)为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比) 的山坡 上发现一棵古树 ,测得古树底端 到山脚点 的距离 ,在距山脚点 处水平距离 的点 处测得古树顶端 的仰角 (古树 与山坡 的剖面、点 在同一平面上,古树 所在直线与直线 垂直),则古树 的高度约为多少米 (结果精确到整数)(数据 ,,)
25.(12分) 如图,已知在锐角三角形 中,,,.
(1)求点 到直线 的距离;
(2)将 绕点 旋转,点 落在点 处,点 落在点 处.
①当点 在边 上时,连接 ,求 的正弦值;
②当 时,求点 与点 的距离,
答案
一
1. C
【解析】直角三角形 中,,,
则 .
2. A
3. B
【解析】,,
,
,
故A选项正确,不符合题意;
, 分别是斜边 上的高和中线,
,,,
,,
,
故B选项不正确,符合题意;
,
,即 ,
,
故C选项正确,不符合题意;
,
,即 ,
,
又 ,
,
故D选项正确,不符合题意.
4. A
【解析】,
.
5. D
6. A
【解析】在 中,,
.
7. B
【解析】连接 ,作 于 .
在 中,
,
,
由翻折可知,,
,
,
是等边三角形,
,
,
,
.
8. B
【解析】延长 交直线 于 ,过 作 ,交直线 于 ,
米.
山坡 的坡度为 ,
,
设 米, 米(),
米
,
米, 米,
米.
,
米,
米.
故选B.
9. A 【解析】过 作 于 ,则四边形 是矩形.
,,
,
,
,
.
10. A
【解析】如图(),过点 作 于点 ,
则 ,
故当 ,即点 与点 重合时, 的形状和大小唯一确定,即C选项不符合题意;
当 时,如图(),
则 ,此时 与 的形状和大小不相同,即选项A符合题意;
当 时, 是等腰三角形,如图(),
此时 的形状与大小确定,故选项D不符合题意;
当 时,如图(),
是钝角三角形,形状与大小确定,故选项B不符合题意.
11. D
【解析】在 中,
因为 ,
所以 ,
因为 ,,
所以 .
12. D
【解析】如图,作 于 , 于 .
易求得 ,,,.
并注意 .
二
13.
【解析】 在 中,,
,,
,,
.
14.
【解析】.
15.
【解析】如图,过点 作 轴交于点 ,
,
,,
.
16.
【解析】,
,
,
.
17.
【解析】,
,
,
上升的高度 (米).
18. 或 或
【解析】如图,点 的位置如图所示:
①若 ,此时点 在 的位置,;
②若 ,此时点 在 , 的位置,,
过点 分别作 ,,垂足为 ,,
设 ,
,
,
在 中,,
即 ,
解得:,(舍去),
,,
,
由四边形 为矩形,可得 ,,
在 中,,
,
,
综上所述, 的长度为 , 或 .
三
19. (1) ();;; .
锐角的正弦值随着角度的增大而增大.
();;;.
锐角的余弦值随着角度的增大而减小.
();;;.
锐角的正切值随着角度的增大而增大.
(2) ①因为 ,
所以 .
②因为 ,
所以 .
20.
21. 过点 作 于点 ,过点 作 于点 ,
设高度为 米.
因为 ,
所以 ,
所以四边形 为矩形.
所以 ,.
由题意可知: 米, 米.
在 中,,
所以 (米).
在 中,,
所以 (米).
所以 ,即 .
解得:.
答:飞机行飞行的高度是 米.
22.
23. 过点 作 于点 ,则 ,
又因为 ,
所以四边形 是平行四边形,,
在 中,
因为 ,
所以 ;
在 中,
因为 ,
所以 ,
因为 ,
所以 ,
解得:,
则 .
答: 的长约为 .
24. 延长 交 的延长线于点 ,则 ,
山坡 上坡度 ,
令 ,则 ,
在 中,由勾股定理得,,
,
解得 ,
,,
,
在 中,,
,
,
古树 的高度约为 .
25. (1) 解 ,可知,,,,
,,,.
(2) ①如备用图 可知: 是等边 .
斜边 .
解 ,作 ,
,
,
,,
.
②Ⅰ.当 在 的右侧时,此时旋转角 ,
延长 交 于点 ,
,
,,,,
.
解 ,作 ,
,,,
.
Ⅱ.当 在 的左侧时,
此时旋转角 ,
是等边 .
.
,, 三点共线.
.
【解析】①方法二:
连接 ,
是顶角为 的等腰 ,
,
,
.
,,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版2022-20203年九年级(下)第一章直角三角形的边角检测试卷A
(时间120分钟,满分120分)
一、(共12小题;每小题3分,共36分)
1. 在 中,,,,那么 等于
A. B. C. D.
2. 如图,某河堤横断面迎水坡 的坡比是 ,堤高 的长为 米,则迎水坡的宽度 的长为
A. 米 B. 米 C. 米 D. 米
3. 如图,在 中,,, 分别是斜边 上的高和中线,下列结论不一定成立的是
A. B.
C. D.
4. 在 中,,那么 等于
A. B. C. D.
5. 如图,在四边形 中,,,,,则
A. B. C. D.
6. 在 中,,,则 的值为
A. B. C. D.
7. 如图, 中,, 在 轴上, 在 轴上,点 , 的坐标分别为 ,,把 沿着 对折得到 ,则点 的坐标为
A. B. C. D.
8. 国家近年来实施了新一轮农村电网改造升级工程,解决了农村供电“最后 公里”问题,电力公司在改造时把某一输电线铁塔建在了一个坡度为 的山坡 的平台 上(如图),测得 , 米, 米, 米,则铁塔 的高度约为(参考数据:,)
A. 米 B. 米 C. 米 D. 米
9. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:
()在点 处放置测角仪,测得旗杆顶的仰角 ;
()量得测角仪的高度 ;
()量得测角仪到旗杆的水平距离 .
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为
A. B. C. D.
10. 在 中,,.下列线段 的长度不能使 的形状和大小都确定的是
A. B. C. D.
11. 如图,在 中,,,,若用科学计算器求 的长,则下列按键顺序正确的是
A. B.
C. D.
12. 如图,垂直于水平面的 信号塔 建在垂直于水平面的悬崖边 点处,某测量员从山脚 点出发沿水平方向前行 米到 点(点 ,, 在同一直线上),再沿斜坡 方向前行 米到 点(点 ,,,, 在同一平面内),在点 处测得 信号塔顶端 的仰角为 ,悬崖 的高为 米,斜坡 的坡度(或坡比),则信号塔 的高度约为
(参考数据:,,)
A. 米 B. 米 C. 米 D. 米
二、(共6小题;每小题4分,共24分)
13. 在 中,若 ,则 的度数是 .
14. .(结果精确到 )
15. 在平面直角坐标系 中,已知点 的坐标为 ,那么直线 与 轴夹角的正切值是 .
16. 若 ,则锐角 .
17. 如图,如果小华沿坡度为 的坡面由 到 行走了 米,那么他实际上升的高度为 米.
18. 定义:有一组对边相等而另一组对边不相等的凸四边形叫做“对等四边形”,如图,在 中,,点 在边 上,点 在边 上,如果 ,,,四边形 为“对等四边形”,那么 的长为 .
三、(共7小题;共60分)
19.(12分)探究规律:
(1)应用计算器算一算.分别比较各个三角函数值的大小,并说一说有什么规律.(精确到 )
() ; ;
; .
规律: .
() ; ;
; .
规律: .
() ; ;
; .
规律: .
(2)拓展应用:
应用上面的规律比较大小.
① ,,,;
② ,,,.
20. (4分)计算:.
21. (8分)如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端 、 的距离,飞机以距海平面垂直同一高度飞行,在点 处测得端点 的俯角为 ,然后沿着平行于 的方向水平飞行了 米,在点 测得端点 的俯角为 ,已知岛屿两端 、 的距离 米,求飞机飞行的高度.(结果精确到 米,参考数据:,)
22(8分)如图,在菱形 中,已知 ,,求菱形 的面积(精确到 ).
(参考数据:,,)
23. (8分)如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口 处测得教学楼顶部 处的仰角为 ,教学楼底部 处的俯角为 ,教学楼的高 .求实验楼与教学楼之间的距离 (结果保留整数).
参考数据:,.
24. (8分)为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比) 的山坡 上发现一棵古树 ,测得古树底端 到山脚点 的距离 ,在距山脚点 处水平距离 的点 处测得古树顶端 的仰角 (古树 与山坡 的剖面、点 在同一平面上,古树 所在直线与直线 垂直),则古树 的高度约为多少米 (结果精确到整数)(数据 ,,)
25.(12分) 如图,已知在锐角三角形 中,,,.
(1)求点 到直线 的距离;
(2)将 绕点 旋转,点 落在点 处,点 落在点 处.
①当点 在边 上时,连接 ,求 的正弦值;
②当 时,求点 与点 的距离,
答案
一
1. C
【解析】直角三角形 中,,,
则 .
2. A
3. B
【解析】,,
,
,
故A选项正确,不符合题意;
, 分别是斜边 上的高和中线,
,,,
,,
,
故B选项不正确,符合题意;
,
,即 ,
,
故C选项正确,不符合题意;
,
,即 ,
,
又 ,
,
故D选项正确,不符合题意.
4. A
【解析】,
.
5. D
6. A
【解析】在 中,,
.
7. B
【解析】连接 ,作 于 .
在 中,
,
,
由翻折可知,,
,
,
是等边三角形,
,
,
,
.
8. B
【解析】延长 交直线 于 ,过 作 ,交直线 于 ,
米.
山坡 的坡度为 ,
,
设 米, 米(),
米
,
米, 米,
米.
,
米,
米.
故选B.
9. A 【解析】过 作 于 ,则四边形 是矩形.
,,
,
,
,
.
10. A
【解析】如图(),过点 作 于点 ,
则 ,
故当 ,即点 与点 重合时, 的形状和大小唯一确定,即C选项不符合题意;
当 时,如图(),
则 ,此时 与 的形状和大小不相同,即选项A符合题意;
当 时, 是等腰三角形,如图(),
此时 的形状与大小确定,故选项D不符合题意;
当 时,如图(),
是钝角三角形,形状与大小确定,故选项B不符合题意.
11. D
【解析】在 中,
因为 ,
所以 ,
因为 ,,
所以 .
12. D
【解析】如图,作 于 , 于 .
易求得 ,,,.
并注意 .
二
13.
【解析】 在 中,,
,,
,,
.
14.
【解析】.
15.
【解析】如图,过点 作 轴交于点 ,
,
,,
.
16.
【解析】,
,
,
.
17.
【解析】,
,
,
上升的高度 (米).
18. 或 或
【解析】如图,点 的位置如图所示:
①若 ,此时点 在 的位置,;
②若 ,此时点 在 , 的位置,,
过点 分别作 ,,垂足为 ,,
设 ,
,
,
在 中,,
即 ,
解得:,(舍去),
,,
,
由四边形 为矩形,可得 ,,
在 中,,
,
,
综上所述, 的长度为 , 或 .
三
19. (1) ();;; .
锐角的正弦值随着角度的增大而增大.
();;;.
锐角的余弦值随着角度的增大而减小.
();;;.
锐角的正切值随着角度的增大而增大.
(2) ①因为 ,
所以 .
②因为 ,
所以 .
20.
21. 过点 作 于点 ,过点 作 于点 ,
设高度为 米.
因为 ,
所以 ,
所以四边形 为矩形.
所以 ,.
由题意可知: 米, 米.
在 中,,
所以 (米).
在 中,,
所以 (米).
所以 ,即 .
解得:.
答:飞机行飞行的高度是 米.
22.
23. 过点 作 于点 ,则 ,
又因为 ,
所以四边形 是平行四边形,,
在 中,
因为 ,
所以 ;
在 中,
因为 ,
所以 ,
因为 ,
所以 ,
解得:,
则 .
答: 的长约为 .
24. 延长 交 的延长线于点 ,则 ,
山坡 上坡度 ,
令 ,则 ,
在 中,由勾股定理得,,
,
解得 ,
,,
,
在 中,,
,
,
古树 的高度约为 .
25. (1) 解 ,可知,,,,
,,,.
(2) ①如备用图 可知: 是等边 .
斜边 .
解 ,作 ,
,
,
,,
.
②Ⅰ.当 在 的右侧时,此时旋转角 ,
延长 交 于点 ,
,
,,,,
.
解 ,作 ,
,,,
.
Ⅱ.当 在 的左侧时,
此时旋转角 ,
是等边 .
.
,, 三点共线.
.
【解析】①方法二:
连接 ,
是顶角为 的等腰 ,
,
,
.
,,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
