广东省梅州市丰顺县潘田中学2022-2023学年九年级下学期2月月考数学试题(含答案)
文档属性
| 名称 | 广东省梅州市丰顺县潘田中学2022-2023学年九年级下学期2月月考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 264.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-08 22:36:29 | ||
图片预览


文档简介
2022-2023学年度第二学期梅州市丰顺县潘田中学九年级数学2月测试题
一、单选题:本大题共10小题,每小题3分,共30分。
1.从一盒写有“水果月饼2枚,巧克力月饼2枚,海苔月饼2枚,蛋黄月饼2枚”的礼饼盒里随机取出一枚,正好是巧克力月饼的概率是( )
A. B. C. D.
2.平面直角坐标系内与点P(﹣2,3)关于原点对称的点的坐标是( )
A.(3,﹣2) B.(2,3)
C.(2,﹣3) D.(﹣3,﹣3)
3.下列交通标志中,是中心对称图形的是( )
A. B.
C. D.
4.小明想用图形1通过作图变换得到图形2,下列这些变化中不可行的是( )
A.轴对称变换 B.平移变换
C.旋转变换 D.中心对称变换
5.若关于x的方程x2+6x+c=0有两个相等的实数根,则c的值是( )
A.36 B.-36 C.9 D.-9
6.将抛物线平移,得到抛物线,下列平移方式中,正确的是( )
A.先向左平移1个单位,再向上平移2个单位
B.先向左平移1个单位,再向下平移2个单位
C.先向右平移1个单位,再向上平移2个单位
D.先向右平移1个单位,再向下平移2个单位
7.如图,一个圆形转盘被平均分成6个全等的扇形,任意旋转这个转盘1次,则当转盘停止转动时,指针指向阴影部分的概率是( )
A. B. C. D.
8.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴为直线x=﹣,结合图象分析下列结论:①abc>0;②当x<0时,y随x的增大而增大;③3a+c>0;④若m,n(m<n)为方程a(x+3)(x﹣2)+3=0的两个根,则m<﹣3且n>2,其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
9.如图,已知点A、B、C、D都在⊙O上,且∠BOD=110°,则∠BCD为( )
A.110° B.115° C.120° D.125°
10.已知抛物线y=ax2+bx+c(0<2a≤b)与x轴最多有一个交点.以下四个结论:
①abc>0;
②该抛物线的对称轴在x=﹣1的右侧;
③关于x的方程ax2+bx+c+1=0无实数根;
④ ≥2.
其中,符合题意结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题:本大题共7小题,每小题4分,共28分。
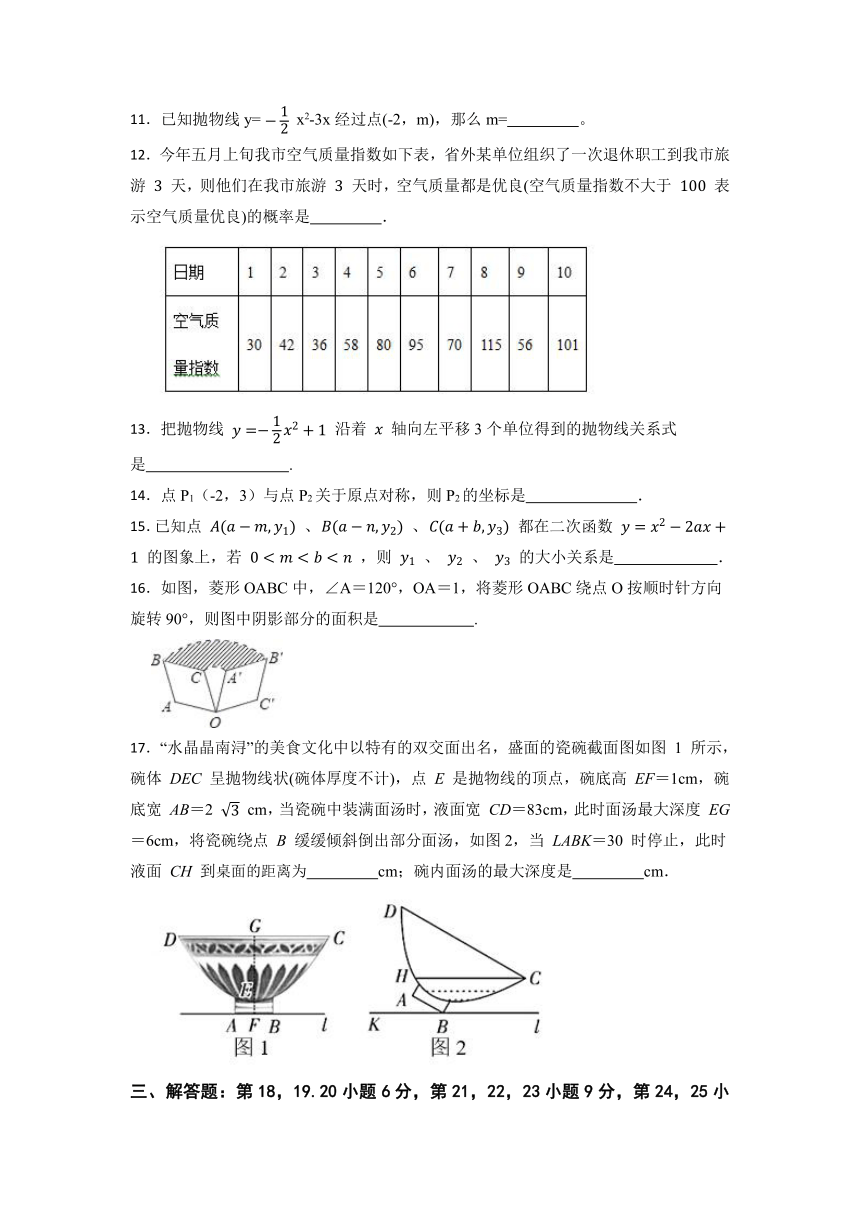
11.已知抛物线y= x2-3x经过点(-2,m),那么m= 。
12.今年五月上旬我市空气质量指数如下表,省外某单位组织了一次退休职工到我市旅游 天,则他们在我市旅游 天时,空气质量都是优良(空气质量指数不大于 表示空气质量优良)的概率是 .
13.把抛物线 沿着 轴向左平移3个单位得到的抛物线关系式是 .
14.点P1(-2,3)与点P2关于原点对称,则P2的坐标是 .
15.已知点 、 、 都在二次函数 的图象上,若 ,则 、 、 的大小关系是 .
16.如图,菱形OABC中,∠A=120°,OA=1,将菱形OABC绕点O按顺时针方向旋转90°,则图中阴影部分的面积是 .
17.“水晶晶南浔”的美食文化中以特有的双交面出名,盛面的瓷碗截面图如图 1 所示,碗体 DEC 呈抛物线状(碗体厚度不计),点 E 是抛物线的顶点,碗底高 EF=1cm,碗底宽 AB=2 cm,当瓷碗中装满面汤时,液面宽 CD=83cm,此时面汤最大深度 EG=6cm,将瓷碗绕点 B 缓缓倾斜倒出部分面汤,如图2,当 LABK=30 时停止,此时液面 CH 到桌面的距离为 cm;碗内面汤的最大深度是 cm.
三、解答题:第18,19.20小题6分,第21,22,23小题9分,第24,25小题10分。
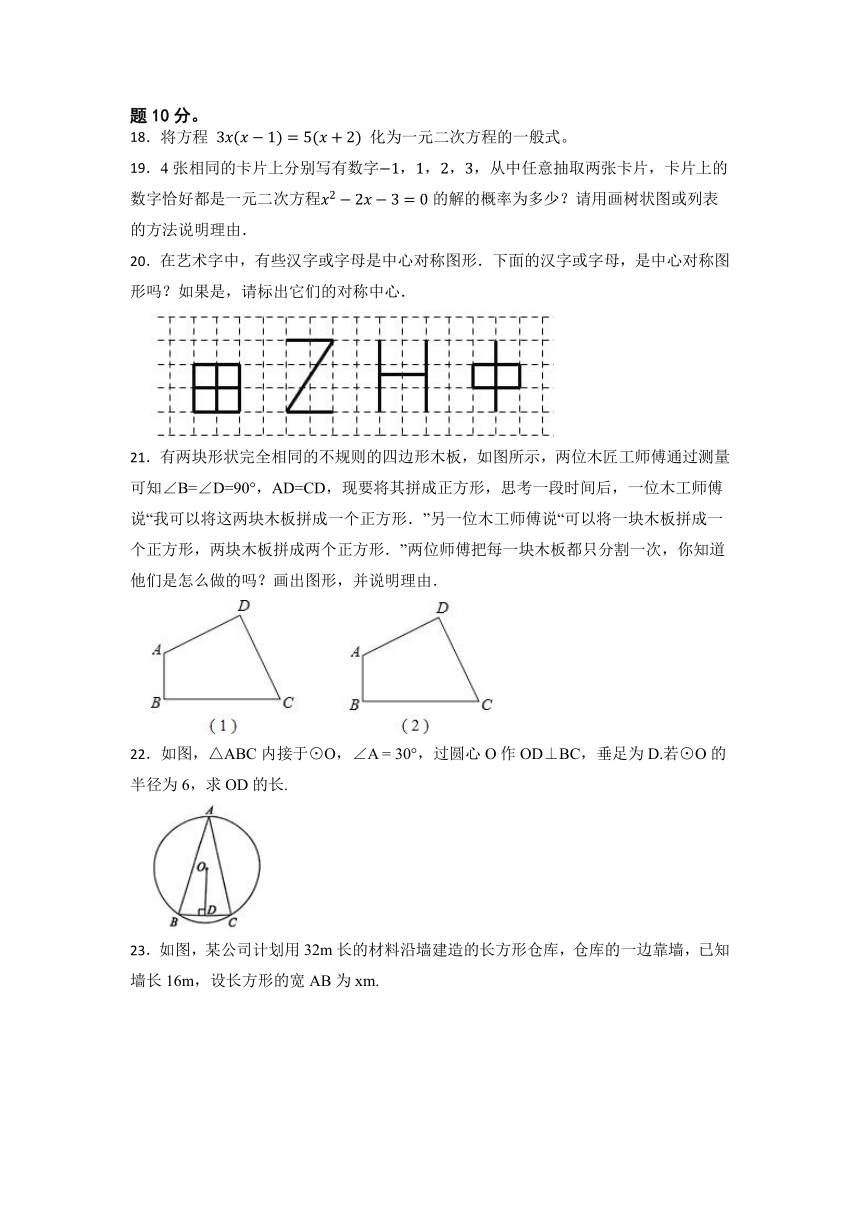
18.将方程 化为一元二次方程的一般式。
19.4张相同的卡片上分别写有数字,,,,从中任意抽取两张卡片,卡片上的数字恰好都是一元二次方程的解的概率为多少?请用画树状图或列表的方法说明理由.
20.在艺术字中,有些汉字或字母是中心对称图形.下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心.
21.有两块形状完全相同的不规则的四边形木板,如图所示,两位木匠工师傅通过测量可知∠B=∠D=90°,AD=CD,现要将其拼成正方形,思考一段时间后,一位木工师傅说“我可以将这两块木板拼成一个正方形.”另一位木工师傅说“可以将一块木板拼成一个正方形,两块木板拼成两个正方形.”两位师傅把每一块木板都只分割一次,你知道他们是怎么做的吗?画出图形,并说明理由.
22.如图,△ABC内接于⊙O,∠A = 30°,过圆心O作OD⊥BC,垂足为D.若⊙O的半径为6,求OD的长.
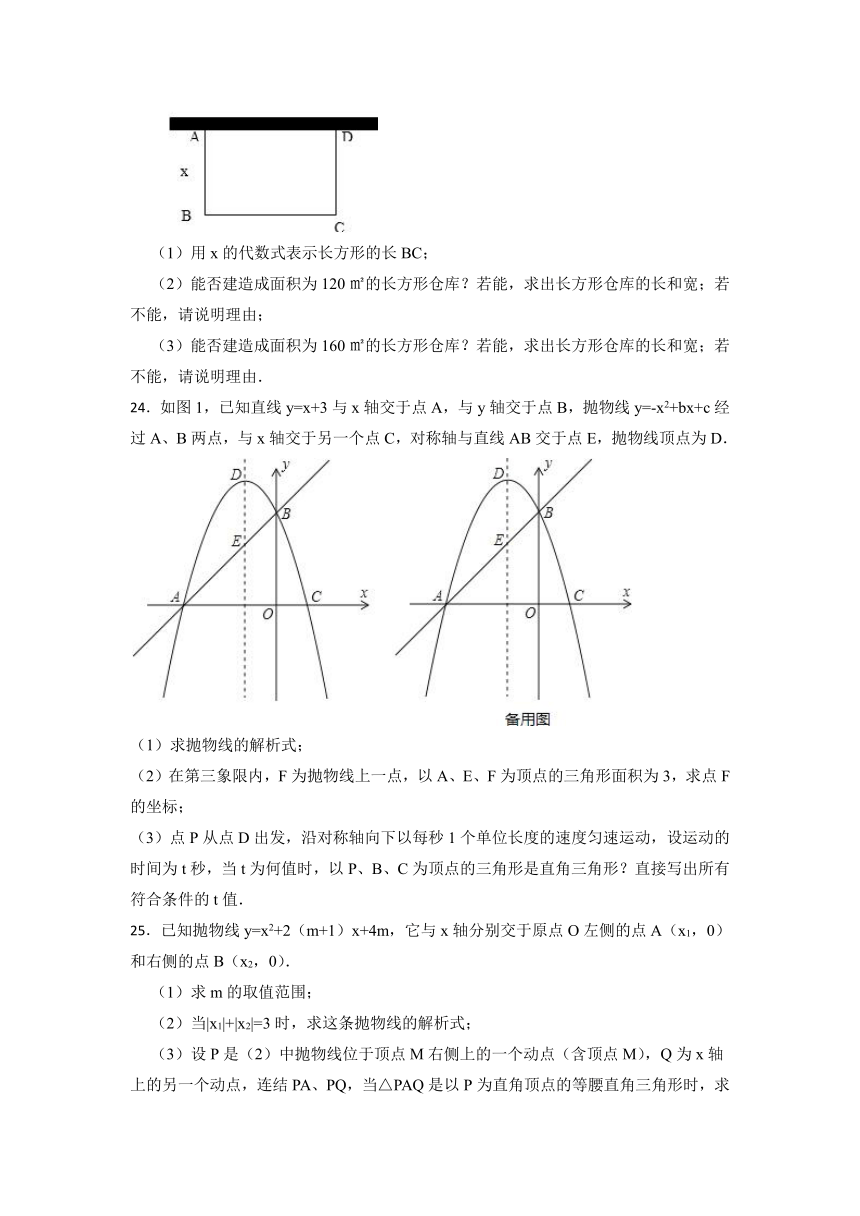
23.如图,某公司计划用32m长的材料沿墙建造的长方形仓库,仓库的一边靠墙,已知墙长16m,设长方形的宽AB为xm.
(1)用x的代数式表示长方形的长BC;
(2)能否建造成面积为120㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由;
(3)能否建造成面积为160㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由.
24.如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=-x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
25.已知抛物线y=x2+2(m+1)x+4m,它与x轴分别交于原点O左侧的点A(x1,0)和右侧的点B(x2,0).
(1)求m的取值范围;
(2)当|x1|+|x2|=3时,求这条抛物线的解析式;
(3)设P是(2)中抛物线位于顶点M右侧上的一个动点(含顶点M),Q为x轴上的另一个动点,连结PA、PQ,当△PAQ是以P为直角顶点的等腰直角三角形时,求P点的坐标.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】D
8.【答案】B
9.【答案】D
10.【答案】C
11.【答案】4
12.【答案】
13.【答案】
14.【答案】(2,-3)
15.【答案】
16.【答案】
17.【答案】;
18.【答案】解:去括号:得: 移项: 合并同类项:
19.【答案】解:解方程得:x1=3,x2=-1,
根据题意画图如下:
共有种等可能的情况数,其中卡片上的数字恰好都是一元二次方程的解的有种,
则从中任意抽取两张卡片,卡片上的数字恰好都是一元二次方程的解的概率为.
20.【答案】解:这些艺术字均为中心对称图形,其对称中心为图形中的点O.
21.【答案】解:如图(1)所示:将两块四边形拼成正方形,
连接BD,将△DBC绕D点顺时针旋转90度,即可得出△B′BD此时三角形是等腰直角三角形,同理可得出正方形B′EBD.如图(2)将一个四边形拼成正方形,过点D作DE⊥BC于点E,过点D作DF⊥BA交BA的延长线于点F,∴∠FDA+∠ADE=∠CDE+∠ADE=90°,∴∠FDA=∠CDE,在△AFD和△CED中, ,
∴△AFD≌△CED(AAS),∴FD=DE,又∵∠B=∠F=∠BED=90°,∴四边形FBED为正方形.
22.【答案】解:连接OB、OC,如图
则OB=OC=6
∵圆周角∠A与圆心角∠BOC对着同一段弧
∴∠BOC=2∠A=60゜
∴△OBC是等边三角形
∴BC=OB=6
∵OD⊥BC
∴
在Rt△ODC中,由勾股定理得:
23.【答案】(1)BC=32-2x
(2)能.
由题知: x(32-2x)=120,
化简整理得(x-6)(x-10)=0,
解得:x1=6,x2=10,
经检验x1=6 ,x2=10都是原方程的解但x1=6时长为20大于墙长,所以不符合题意,舍去,
答:能建成面积为120㎡仓库,此时长为12米,宽为10米.
(3)不能.
由题知: x(32-2x)=160
化简整理得:x2-16x+80=0,
此时b2-4ac=162-4×1×80=-64, 此方程无解
所以不能建造成面积为160㎡的长方形仓库.
24.【答案】解:(1)∵y=x+3与x轴交于点A,与y轴交于点B,∴当y=0时,x=-3,即A点坐标为(-3,0),当x=0时,y=3,即B点坐标为(0,3),将A(-3,0),B(0,3)代入y=-x2+bx+c,得:, 解得:,∴抛物线的解析式为:y=-x2-2x+3;(2)如图1,设第三象限内的点F的坐标为(m,-m2-2m+3),则m<0,-m2-2m+3<0.∵y=-x2-2x+3=-(x+1)2+4,∴对称轴为直线x=-1,顶点D的坐标为(-1,4),设抛物线的对称轴与x轴交于点G,连接FG,则G(-1,0),AG=2.∵直线AB的解析式为y=x+3,∴当x=-1时,y=-1+3=2,∴E点坐标为(-1,2).∵S△AEF=S△AEG+S△AFG-S△EFG=×2×2+×2×(m2+2m-3)-×2×(-1-m)=m2+3m,∴以A、E、F为顶点的三角形面积为3时,m2+3m=3,解得:,(舍去),当时,-m2-2m+3=-m2-3m+m+3=-3+m+3=m=,∴点F的坐标为(,);(3)设P点坐标为(-1,n).∵B(0,3),C(1,0),∴BC2=12+32=10.分三种情况:①如图2,如果∠PBC=90°,那么PB2+BC2=PC2,即(0+1)2+(n-3)2+10=(1+1)2+(n-0)2,化简整理得6n=16,解得n=,∴P点坐标为(-1,),∵顶点D的坐标为(-1,4),∴PD=4-=,∵点P的速度为每秒1个单位长度,∴t1=;②如图3,如果∠BPC=90°,那么PB2+PC2=BC2,即(0+1)2+(n-3)2+(1+1)2+(n-0)2=10,化简整理得n2-3n+2=0,解得n=2或1,∴P点坐标为(-1,2)或(-1,1),∵顶点D的坐标为(-1,4),∴PD=4-2=2或PD=4-1=3,∵点P的速度为每秒1个单位长度,∴t2=2,t3=3;③如图4,如果∠BCP=90°,那么BC2+PC2=PB2,即10+(1+1)2+(n-0)2=(0+1)2+(n-3)2,化简整理得6n=-4,解得n=-,∴P点坐标为(-1,-),∵顶点D的坐标为(-1,4),∴PD=4+=,∵点P的速度为每秒1个单位长度,∴t4=;综上可知,当t为秒或2秒或3秒或秒时,以P、B、C为顶点的三角形是直角三角形.
25.【答案】解:(1)∵抛物线开口向上,与y轴的交点在x轴下方,
∴4m<0,
∴m<0;
(2)根据根与系数的关系得到x1+x2=﹣2(m+1),x1x2=4m,
∵x1<0,x2>0,
而|x1|+|x2|=3,
∴﹣x1+x2=3,
∴(x1+x2)2﹣4x1x2=9,
即4(m+1)2﹣16m=9,解得m1=(舍去),m2=﹣,
∴m=﹣,
∴抛物线解析式为y=x2+x﹣2;
(3)抛物线的对称轴为直线x=﹣,
过P点作PH⊥x轴于H,如图,
设P(x,x2+x﹣2)(x≥﹣),
∵△PAQ是以P为直角顶点的等腰直角三角形,
∴PH=AH,
∴|x2+x﹣2|=x+2,
当x2+x﹣2=x+2,解得x1=﹣2(舍去),x2=2,此时P点坐标为(2,4);
当x2+x﹣2=﹣x﹣2,解得x1=﹣2(舍去),x2=0,此时P点坐标为(0,2),
即满足条件的P点坐标为(2,4)或(0,2).
一、单选题:本大题共10小题,每小题3分,共30分。
1.从一盒写有“水果月饼2枚,巧克力月饼2枚,海苔月饼2枚,蛋黄月饼2枚”的礼饼盒里随机取出一枚,正好是巧克力月饼的概率是( )
A. B. C. D.
2.平面直角坐标系内与点P(﹣2,3)关于原点对称的点的坐标是( )
A.(3,﹣2) B.(2,3)
C.(2,﹣3) D.(﹣3,﹣3)
3.下列交通标志中,是中心对称图形的是( )
A. B.
C. D.
4.小明想用图形1通过作图变换得到图形2,下列这些变化中不可行的是( )
A.轴对称变换 B.平移变换
C.旋转变换 D.中心对称变换
5.若关于x的方程x2+6x+c=0有两个相等的实数根,则c的值是( )
A.36 B.-36 C.9 D.-9
6.将抛物线平移,得到抛物线,下列平移方式中,正确的是( )
A.先向左平移1个单位,再向上平移2个单位
B.先向左平移1个单位,再向下平移2个单位
C.先向右平移1个单位,再向上平移2个单位
D.先向右平移1个单位,再向下平移2个单位
7.如图,一个圆形转盘被平均分成6个全等的扇形,任意旋转这个转盘1次,则当转盘停止转动时,指针指向阴影部分的概率是( )
A. B. C. D.
8.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴为直线x=﹣,结合图象分析下列结论:①abc>0;②当x<0时,y随x的增大而增大;③3a+c>0;④若m,n(m<n)为方程a(x+3)(x﹣2)+3=0的两个根,则m<﹣3且n>2,其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
9.如图,已知点A、B、C、D都在⊙O上,且∠BOD=110°,则∠BCD为( )
A.110° B.115° C.120° D.125°
10.已知抛物线y=ax2+bx+c(0<2a≤b)与x轴最多有一个交点.以下四个结论:
①abc>0;
②该抛物线的对称轴在x=﹣1的右侧;
③关于x的方程ax2+bx+c+1=0无实数根;
④ ≥2.
其中,符合题意结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题:本大题共7小题,每小题4分,共28分。
11.已知抛物线y= x2-3x经过点(-2,m),那么m= 。
12.今年五月上旬我市空气质量指数如下表,省外某单位组织了一次退休职工到我市旅游 天,则他们在我市旅游 天时,空气质量都是优良(空气质量指数不大于 表示空气质量优良)的概率是 .
13.把抛物线 沿着 轴向左平移3个单位得到的抛物线关系式是 .
14.点P1(-2,3)与点P2关于原点对称,则P2的坐标是 .
15.已知点 、 、 都在二次函数 的图象上,若 ,则 、 、 的大小关系是 .
16.如图,菱形OABC中,∠A=120°,OA=1,将菱形OABC绕点O按顺时针方向旋转90°,则图中阴影部分的面积是 .
17.“水晶晶南浔”的美食文化中以特有的双交面出名,盛面的瓷碗截面图如图 1 所示,碗体 DEC 呈抛物线状(碗体厚度不计),点 E 是抛物线的顶点,碗底高 EF=1cm,碗底宽 AB=2 cm,当瓷碗中装满面汤时,液面宽 CD=83cm,此时面汤最大深度 EG=6cm,将瓷碗绕点 B 缓缓倾斜倒出部分面汤,如图2,当 LABK=30 时停止,此时液面 CH 到桌面的距离为 cm;碗内面汤的最大深度是 cm.
三、解答题:第18,19.20小题6分,第21,22,23小题9分,第24,25小题10分。
18.将方程 化为一元二次方程的一般式。
19.4张相同的卡片上分别写有数字,,,,从中任意抽取两张卡片,卡片上的数字恰好都是一元二次方程的解的概率为多少?请用画树状图或列表的方法说明理由.
20.在艺术字中,有些汉字或字母是中心对称图形.下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心.
21.有两块形状完全相同的不规则的四边形木板,如图所示,两位木匠工师傅通过测量可知∠B=∠D=90°,AD=CD,现要将其拼成正方形,思考一段时间后,一位木工师傅说“我可以将这两块木板拼成一个正方形.”另一位木工师傅说“可以将一块木板拼成一个正方形,两块木板拼成两个正方形.”两位师傅把每一块木板都只分割一次,你知道他们是怎么做的吗?画出图形,并说明理由.
22.如图,△ABC内接于⊙O,∠A = 30°,过圆心O作OD⊥BC,垂足为D.若⊙O的半径为6,求OD的长.
23.如图,某公司计划用32m长的材料沿墙建造的长方形仓库,仓库的一边靠墙,已知墙长16m,设长方形的宽AB为xm.
(1)用x的代数式表示长方形的长BC;
(2)能否建造成面积为120㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由;
(3)能否建造成面积为160㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由.
24.如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=-x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
25.已知抛物线y=x2+2(m+1)x+4m,它与x轴分别交于原点O左侧的点A(x1,0)和右侧的点B(x2,0).
(1)求m的取值范围;
(2)当|x1|+|x2|=3时,求这条抛物线的解析式;
(3)设P是(2)中抛物线位于顶点M右侧上的一个动点(含顶点M),Q为x轴上的另一个动点,连结PA、PQ,当△PAQ是以P为直角顶点的等腰直角三角形时,求P点的坐标.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】D
8.【答案】B
9.【答案】D
10.【答案】C
11.【答案】4
12.【答案】
13.【答案】
14.【答案】(2,-3)
15.【答案】
16.【答案】
17.【答案】;
18.【答案】解:去括号:得: 移项: 合并同类项:
19.【答案】解:解方程得:x1=3,x2=-1,
根据题意画图如下:
共有种等可能的情况数,其中卡片上的数字恰好都是一元二次方程的解的有种,
则从中任意抽取两张卡片,卡片上的数字恰好都是一元二次方程的解的概率为.
20.【答案】解:这些艺术字均为中心对称图形,其对称中心为图形中的点O.
21.【答案】解:如图(1)所示:将两块四边形拼成正方形,
连接BD,将△DBC绕D点顺时针旋转90度,即可得出△B′BD此时三角形是等腰直角三角形,同理可得出正方形B′EBD.如图(2)将一个四边形拼成正方形,过点D作DE⊥BC于点E,过点D作DF⊥BA交BA的延长线于点F,∴∠FDA+∠ADE=∠CDE+∠ADE=90°,∴∠FDA=∠CDE,在△AFD和△CED中, ,
∴△AFD≌△CED(AAS),∴FD=DE,又∵∠B=∠F=∠BED=90°,∴四边形FBED为正方形.
22.【答案】解:连接OB、OC,如图
则OB=OC=6
∵圆周角∠A与圆心角∠BOC对着同一段弧
∴∠BOC=2∠A=60゜
∴△OBC是等边三角形
∴BC=OB=6
∵OD⊥BC
∴
在Rt△ODC中,由勾股定理得:
23.【答案】(1)BC=32-2x
(2)能.
由题知: x(32-2x)=120,
化简整理得(x-6)(x-10)=0,
解得:x1=6,x2=10,
经检验x1=6 ,x2=10都是原方程的解但x1=6时长为20大于墙长,所以不符合题意,舍去,
答:能建成面积为120㎡仓库,此时长为12米,宽为10米.
(3)不能.
由题知: x(32-2x)=160
化简整理得:x2-16x+80=0,
此时b2-4ac=162-4×1×80=-64, 此方程无解
所以不能建造成面积为160㎡的长方形仓库.
24.【答案】解:(1)∵y=x+3与x轴交于点A,与y轴交于点B,∴当y=0时,x=-3,即A点坐标为(-3,0),当x=0时,y=3,即B点坐标为(0,3),将A(-3,0),B(0,3)代入y=-x2+bx+c,得:, 解得:,∴抛物线的解析式为:y=-x2-2x+3;(2)如图1,设第三象限内的点F的坐标为(m,-m2-2m+3),则m<0,-m2-2m+3<0.∵y=-x2-2x+3=-(x+1)2+4,∴对称轴为直线x=-1,顶点D的坐标为(-1,4),设抛物线的对称轴与x轴交于点G,连接FG,则G(-1,0),AG=2.∵直线AB的解析式为y=x+3,∴当x=-1时,y=-1+3=2,∴E点坐标为(-1,2).∵S△AEF=S△AEG+S△AFG-S△EFG=×2×2+×2×(m2+2m-3)-×2×(-1-m)=m2+3m,∴以A、E、F为顶点的三角形面积为3时,m2+3m=3,解得:,(舍去),当时,-m2-2m+3=-m2-3m+m+3=-3+m+3=m=,∴点F的坐标为(,);(3)设P点坐标为(-1,n).∵B(0,3),C(1,0),∴BC2=12+32=10.分三种情况:①如图2,如果∠PBC=90°,那么PB2+BC2=PC2,即(0+1)2+(n-3)2+10=(1+1)2+(n-0)2,化简整理得6n=16,解得n=,∴P点坐标为(-1,),∵顶点D的坐标为(-1,4),∴PD=4-=,∵点P的速度为每秒1个单位长度,∴t1=;②如图3,如果∠BPC=90°,那么PB2+PC2=BC2,即(0+1)2+(n-3)2+(1+1)2+(n-0)2=10,化简整理得n2-3n+2=0,解得n=2或1,∴P点坐标为(-1,2)或(-1,1),∵顶点D的坐标为(-1,4),∴PD=4-2=2或PD=4-1=3,∵点P的速度为每秒1个单位长度,∴t2=2,t3=3;③如图4,如果∠BCP=90°,那么BC2+PC2=PB2,即10+(1+1)2+(n-0)2=(0+1)2+(n-3)2,化简整理得6n=-4,解得n=-,∴P点坐标为(-1,-),∵顶点D的坐标为(-1,4),∴PD=4+=,∵点P的速度为每秒1个单位长度,∴t4=;综上可知,当t为秒或2秒或3秒或秒时,以P、B、C为顶点的三角形是直角三角形.
25.【答案】解:(1)∵抛物线开口向上,与y轴的交点在x轴下方,
∴4m<0,
∴m<0;
(2)根据根与系数的关系得到x1+x2=﹣2(m+1),x1x2=4m,
∵x1<0,x2>0,
而|x1|+|x2|=3,
∴﹣x1+x2=3,
∴(x1+x2)2﹣4x1x2=9,
即4(m+1)2﹣16m=9,解得m1=(舍去),m2=﹣,
∴m=﹣,
∴抛物线解析式为y=x2+x﹣2;
(3)抛物线的对称轴为直线x=﹣,
过P点作PH⊥x轴于H,如图,
设P(x,x2+x﹣2)(x≥﹣),
∵△PAQ是以P为直角顶点的等腰直角三角形,
∴PH=AH,
∴|x2+x﹣2|=x+2,
当x2+x﹣2=x+2,解得x1=﹣2(舍去),x2=2,此时P点坐标为(2,4);
当x2+x﹣2=﹣x﹣2,解得x1=﹣2(舍去),x2=0,此时P点坐标为(0,2),
即满足条件的P点坐标为(2,4)或(0,2).
同课章节目录
