【解析版】湖南省张家界市一中2013-2014学年高一下学期第一次月考数学试题
文档属性
| 名称 | 【解析版】湖南省张家界市一中2013-2014学年高一下学期第一次月考数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 538.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-20 07:44:47 | ||
图片预览



文档简介
第Ⅰ卷(共50分)
一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是( )
A.球 B.三棱锥 C.正方体 D.圆柱
2.如图所示,用符号语言可表达为( )
A. B.
C. D.
3.用、、表示三条不同的直线,表示平面,给出下列命题:
①若∥,∥,则∥; ②若⊥,⊥,则⊥;③若∥,∥,则∥;
④若⊥,⊥,则∥.其中正确命题的序号是( )
A. ①② B. ②③ C. ①④ D.③④
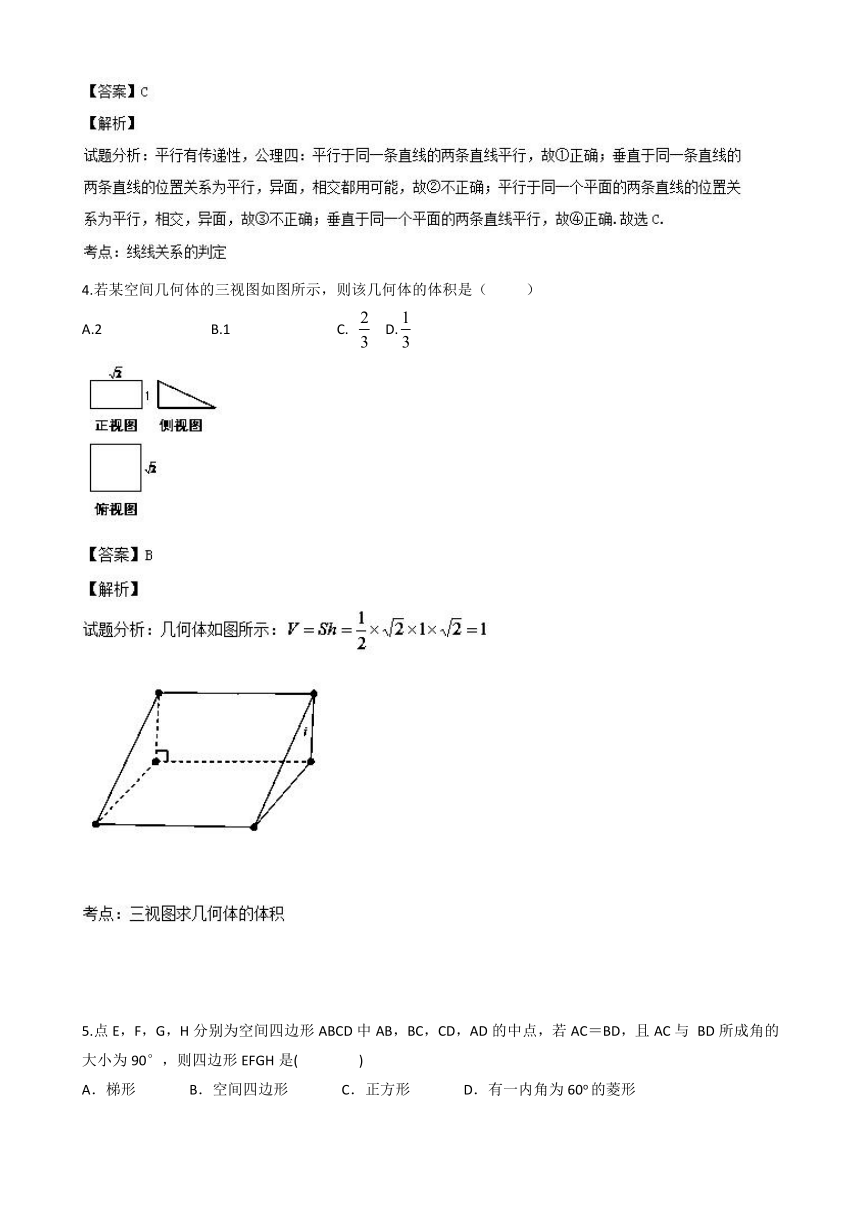
4.若某空间几何体的三视图如图所示,则该几何体的体积是( )
A.2 B.1 C. D.
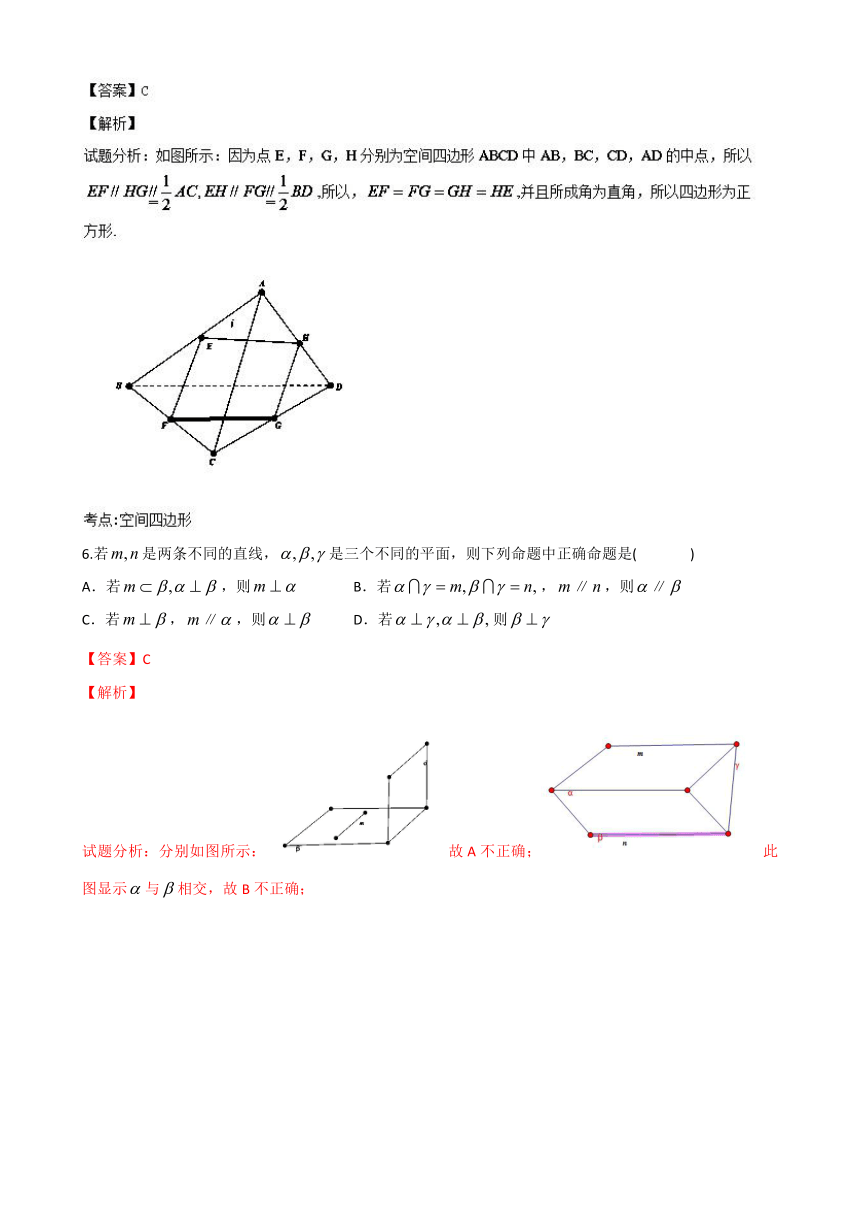
5.点E,F,G,H分别为空间四边形ABCD中AB,BC,CD,AD的中点,若AC=BD,且AC与 BD所成角的大小为90°,则四边形EFGH是( )
A.梯形 B.空间四边形 C.正方形 D.有一内角为60o的菱形
6.若是两条不同的直线,是三个不同的平面,则下列命题中正确命题是( )
A.若,则 B.若,∥,则∥
C.若,∥,则 D.若则
【答案】C
【解析】
试题分析:分别如图所示:故A不正确;此图显示与相交,故B不正确;
7.以A(1,3),B(-5,1)为端点的线段的垂直平分线方程是( )
A. 3x-y+8=0 B. 3x+y+4=0 C . 3x-y+6=0 D. 3x+y+2=0
8.如果一个水平放置的图形的斜二测直观图是一个底面为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )
A. B. C. D.
【答案】A
【解析】
试题分析:根据,等腰梯形的面积为,所以原图像的面积为,故选A.
考点:斜二测画法
9.将边长为的正方形沿对角线折起,使,则三棱锥的体积为( )
A. B. C. D.
10.已知直线过点且与线段相交,那么直线的斜率的取值范围是( )
A. B. C. D.
【答案】A
【解析】
第Ⅱ卷(共90分)
二、填空题(每题5分,满分25分,将答案填在答题纸上)
11.直线的倾斜角的大小为 。
【答案】
【解析】
试题分析:,所以倾斜角为.
考点:1.直线方程;2.倾斜角和斜率.
12.一个高为2的圆柱,底面周长为,该圆柱的表面积为________.
【答案】
【解析】
试题分析:设底面半径,,,.
考点:圆柱表面积
13.如图,已知正方体中,分别是的中点.
则直线和所成的角为__________.
14.如图,二面角的大小是60°,线段,在上, 与所成的角为30°,则
【答案】
【解析】
15.棱长为1的正方体的8个顶点都在球的表面上,分别是棱的中点,点,分别是线段,(不包括端点)上的动点,且线段平行于平面,则
(1)直线被球截得的线段长为__________________.
(2)四面体的体积的最大值是
【答案】(1);(2).
【解析】
试题分析:(1)因为点在圆上,为中点,所以直线被球截得的线段长为正方形的外接圆直径,等于,(2)过做与点,连接∵,,
平面∥平面,为平面与两平行平面的交线,
,又,,平面,
三、解答题 (本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)
16.(本小题满分12分)
(1)当为何值时,直线与直线平行?
(2)当为何值时,直线与直线垂直?
17.(本小题满分12分)
(1)求经过点A(3,2),B(-2,0)的直线方程。
(2)求过点P(-1,3),并且在两轴上的截距相等的直线方程;
18.(本小题满分12分)
已知圆台的上、下底面半径分别是2、6,且侧面面积等于两底面面积之和。
(Ⅰ)求该圆台的母线长;(Ⅱ)求该圆台的体积。
(Ⅱ)由(Ⅰ)可求得,圆台的高为.8分
∴ == 12分
考点:圆台的表面积和体积
19.(本小题满分13分)
如图所示,在三棱柱中,,,点分别是的中点.
(1)求证:平面∥平面;
(2)求证:平面⊥平面;
(3)若,,求异面直线所成的角。
【答案】详见解析
【解析】
试题分析:(1)根据平面几何可证,可证得面面垂直;(2)根据D是AB的中点,可证面,证得面面垂直;(3)异面直线所成的角,转化成相交直线所成的角,然后在所在三角形内解决角的问题.
考点:1.面面垂直的判定;2.面面平行的判定;3.异面直线所成的角.
20.(本小题满分13分)
如图,在等腰直角三角形中, =900 ,=6, 分别是,上的点, 为的中点.将沿折起,得到如图所示的四棱椎,其中
(1)证明:;
(2)求二面角的平面角的余弦值.
证明: (1)设F为ED的中点,连接OF,A’F,计算得A’F=2,OF=1
∵A’F为等腰△A’DE底边的中线,∴A’F⊥DE
∵OF在原等腰△ABC底边BC的高线上,
∴OF⊥DE
又∵A’F,OF平面A’OF, A’FOF=F,
∴DE⊥平面A’OF
∵A’O平面A’OF, ∴DE⊥A’O
在△A’FO中,A’+=3+1=,∴A’O⊥OF
∵OFDE=F,OF平面BCDE,DE平面BCDE, ∴A’O⊥平面BCDE 6分
21.(本小题满分13分)
如图,是圆的直径,点是圆上异于的点,直线 分别为的中点。
(Ⅰ)记平面与平面的交线为,试判断与平面的位置关系,并加以说明;
(Ⅱ)设(Ⅰ)中的直线与圆的另一个交点为,且点满足,记直线
平面所成的角为异面直线与所成的锐角为,二面角的大小为
1 求证:
②当点为弧的中点时,,求直线与平面所成的角的正弦值。
【答案】详见解析
【解析】
,且平面平面,所以∥. 因为平面,平面,所以直线∥平面..4分
(Ⅱ)①
证明:如图,
连接,由(Ⅰ)可知交线即为直线,且∥. 因为是的直径,所以,于是.
已知平面,而平面,所以.而,所以平面.连接,,因为平面,所以.故就是二面角的平面角,即. 由,作∥,且. 连接,,因为是的中点,,所以,
从而四边形是平行四边形,∥.连接,因为平面,所以是在平面内的射影,故就是直线与平面所成的角,即. 又平面,有,知为锐角,故为异面直线与所成的角,即, 8 分
于是在△,△,△中,分别可得,,,
从而,即. 9分
②因为∥,所以直线与平面所成的角就为CF与平面所成的角
过点C作CG⊥BF,垂足为G,因为平面所以CG,又所以CG⊥平面
故就是直线与平面所成的角, 故直线与平面所成的角的正弦值为 13分
考点:1.线面平行的判定;2线面平行的性质;3.线面垂直的判定;4.二面角;5.线面角.
一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是( )
A.球 B.三棱锥 C.正方体 D.圆柱
2.如图所示,用符号语言可表达为( )
A. B.
C. D.
3.用、、表示三条不同的直线,表示平面,给出下列命题:
①若∥,∥,则∥; ②若⊥,⊥,则⊥;③若∥,∥,则∥;
④若⊥,⊥,则∥.其中正确命题的序号是( )
A. ①② B. ②③ C. ①④ D.③④
4.若某空间几何体的三视图如图所示,则该几何体的体积是( )
A.2 B.1 C. D.
5.点E,F,G,H分别为空间四边形ABCD中AB,BC,CD,AD的中点,若AC=BD,且AC与 BD所成角的大小为90°,则四边形EFGH是( )
A.梯形 B.空间四边形 C.正方形 D.有一内角为60o的菱形
6.若是两条不同的直线,是三个不同的平面,则下列命题中正确命题是( )
A.若,则 B.若,∥,则∥
C.若,∥,则 D.若则
【答案】C
【解析】
试题分析:分别如图所示:故A不正确;此图显示与相交,故B不正确;
7.以A(1,3),B(-5,1)为端点的线段的垂直平分线方程是( )
A. 3x-y+8=0 B. 3x+y+4=0 C . 3x-y+6=0 D. 3x+y+2=0
8.如果一个水平放置的图形的斜二测直观图是一个底面为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )
A. B. C. D.
【答案】A
【解析】
试题分析:根据,等腰梯形的面积为,所以原图像的面积为,故选A.
考点:斜二测画法
9.将边长为的正方形沿对角线折起,使,则三棱锥的体积为( )
A. B. C. D.
10.已知直线过点且与线段相交,那么直线的斜率的取值范围是( )
A. B. C. D.
【答案】A
【解析】
第Ⅱ卷(共90分)
二、填空题(每题5分,满分25分,将答案填在答题纸上)
11.直线的倾斜角的大小为 。
【答案】
【解析】
试题分析:,所以倾斜角为.
考点:1.直线方程;2.倾斜角和斜率.
12.一个高为2的圆柱,底面周长为,该圆柱的表面积为________.
【答案】
【解析】
试题分析:设底面半径,,,.
考点:圆柱表面积
13.如图,已知正方体中,分别是的中点.
则直线和所成的角为__________.
14.如图,二面角的大小是60°,线段,在上, 与所成的角为30°,则
【答案】
【解析】
15.棱长为1的正方体的8个顶点都在球的表面上,分别是棱的中点,点,分别是线段,(不包括端点)上的动点,且线段平行于平面,则
(1)直线被球截得的线段长为__________________.
(2)四面体的体积的最大值是
【答案】(1);(2).
【解析】
试题分析:(1)因为点在圆上,为中点,所以直线被球截得的线段长为正方形的外接圆直径,等于,(2)过做与点,连接∵,,
平面∥平面,为平面与两平行平面的交线,
,又,,平面,
三、解答题 (本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)
16.(本小题满分12分)
(1)当为何值时,直线与直线平行?
(2)当为何值时,直线与直线垂直?
17.(本小题满分12分)
(1)求经过点A(3,2),B(-2,0)的直线方程。
(2)求过点P(-1,3),并且在两轴上的截距相等的直线方程;
18.(本小题满分12分)
已知圆台的上、下底面半径分别是2、6,且侧面面积等于两底面面积之和。
(Ⅰ)求该圆台的母线长;(Ⅱ)求该圆台的体积。
(Ⅱ)由(Ⅰ)可求得,圆台的高为.8分
∴ == 12分
考点:圆台的表面积和体积
19.(本小题满分13分)
如图所示,在三棱柱中,,,点分别是的中点.
(1)求证:平面∥平面;
(2)求证:平面⊥平面;
(3)若,,求异面直线所成的角。
【答案】详见解析
【解析】
试题分析:(1)根据平面几何可证,可证得面面垂直;(2)根据D是AB的中点,可证面,证得面面垂直;(3)异面直线所成的角,转化成相交直线所成的角,然后在所在三角形内解决角的问题.
考点:1.面面垂直的判定;2.面面平行的判定;3.异面直线所成的角.
20.(本小题满分13分)
如图,在等腰直角三角形中, =900 ,=6, 分别是,上的点, 为的中点.将沿折起,得到如图所示的四棱椎,其中
(1)证明:;
(2)求二面角的平面角的余弦值.
证明: (1)设F为ED的中点,连接OF,A’F,计算得A’F=2,OF=1
∵A’F为等腰△A’DE底边的中线,∴A’F⊥DE
∵OF在原等腰△ABC底边BC的高线上,
∴OF⊥DE
又∵A’F,OF平面A’OF, A’FOF=F,
∴DE⊥平面A’OF
∵A’O平面A’OF, ∴DE⊥A’O
在△A’FO中,A’+=3+1=,∴A’O⊥OF
∵OFDE=F,OF平面BCDE,DE平面BCDE, ∴A’O⊥平面BCDE 6分
21.(本小题满分13分)
如图,是圆的直径,点是圆上异于的点,直线 分别为的中点。
(Ⅰ)记平面与平面的交线为,试判断与平面的位置关系,并加以说明;
(Ⅱ)设(Ⅰ)中的直线与圆的另一个交点为,且点满足,记直线
平面所成的角为异面直线与所成的锐角为,二面角的大小为
1 求证:
②当点为弧的中点时,,求直线与平面所成的角的正弦值。
【答案】详见解析
【解析】
,且平面平面,所以∥. 因为平面,平面,所以直线∥平面..4分
(Ⅱ)①
证明:如图,
连接,由(Ⅰ)可知交线即为直线,且∥. 因为是的直径,所以,于是.
已知平面,而平面,所以.而,所以平面.连接,,因为平面,所以.故就是二面角的平面角,即. 由,作∥,且. 连接,,因为是的中点,,所以,
从而四边形是平行四边形,∥.连接,因为平面,所以是在平面内的射影,故就是直线与平面所成的角,即. 又平面,有,知为锐角,故为异面直线与所成的角,即, 8 分
于是在△,△,△中,分别可得,,,
从而,即. 9分
②因为∥,所以直线与平面所成的角就为CF与平面所成的角
过点C作CG⊥BF,垂足为G,因为平面所以CG,又所以CG⊥平面
故就是直线与平面所成的角, 故直线与平面所成的角的正弦值为 13分
考点:1.线面平行的判定;2线面平行的性质;3.线面垂直的判定;4.二面角;5.线面角.
同课章节目录
