2023年重庆市大渡口区初九年级第一次适应性检测数学试题(无答案)
文档属性
| 名称 | 2023年重庆市大渡口区初九年级第一次适应性检测数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 530.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 21:17:55 | ||
图片预览


文档简介
大渡口区初2023级第一次适应性检测
数学试题
(全卷共三个大题,满分150分,考试时间120分钟)
1.试题卷上各题的答案用钢笔或圆珠笔书写在答题卡上,不得在试题卷上直接作答;
2.答题前认真阅读答题卡上的注意事项:
3.作图(包括作辅助线)请一律用黑色的签字笔完成.
一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上对应题目的正确答案标号涂黑.
1.正方形的边长为,则它的面积为( )
A. B. C. D.
2.下面四个关系式中,y是x的反比例函数的是( )
A. B. C. D.
3.矩形中,,则的长为( )
A.5 B.4 C.3 D.2
4.如图,曲线反映了某地一天气温随时间的变化情况,则这一天的最高温度约为( )
A. B. C. D.
5.如图,与位似,点O为位似中心,,,则的长是( )
A.12 B.10 C.8 D.6
6.在一个不透明的箱子里装有m个球,其中红球4个,这些球除颜色外都相同,每次将球搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验后发现,摸到红球的频率在0.2,那么可以估算出m的值为( )
A.8 B.12 C.16 D.20
7.估算的结果( )
A.在6和7之间 B.在7和8之间 C.在8和9之间 D.在9和10之间
8.某商店3月份的销售额是3万元,5月份的销售额是3.63万元,求商店这两个月销售额月平均增长率.设商店这两个月销售额月平均增长率为x,根据题意,下面所列方程正确的是( )
A. B. C. D.
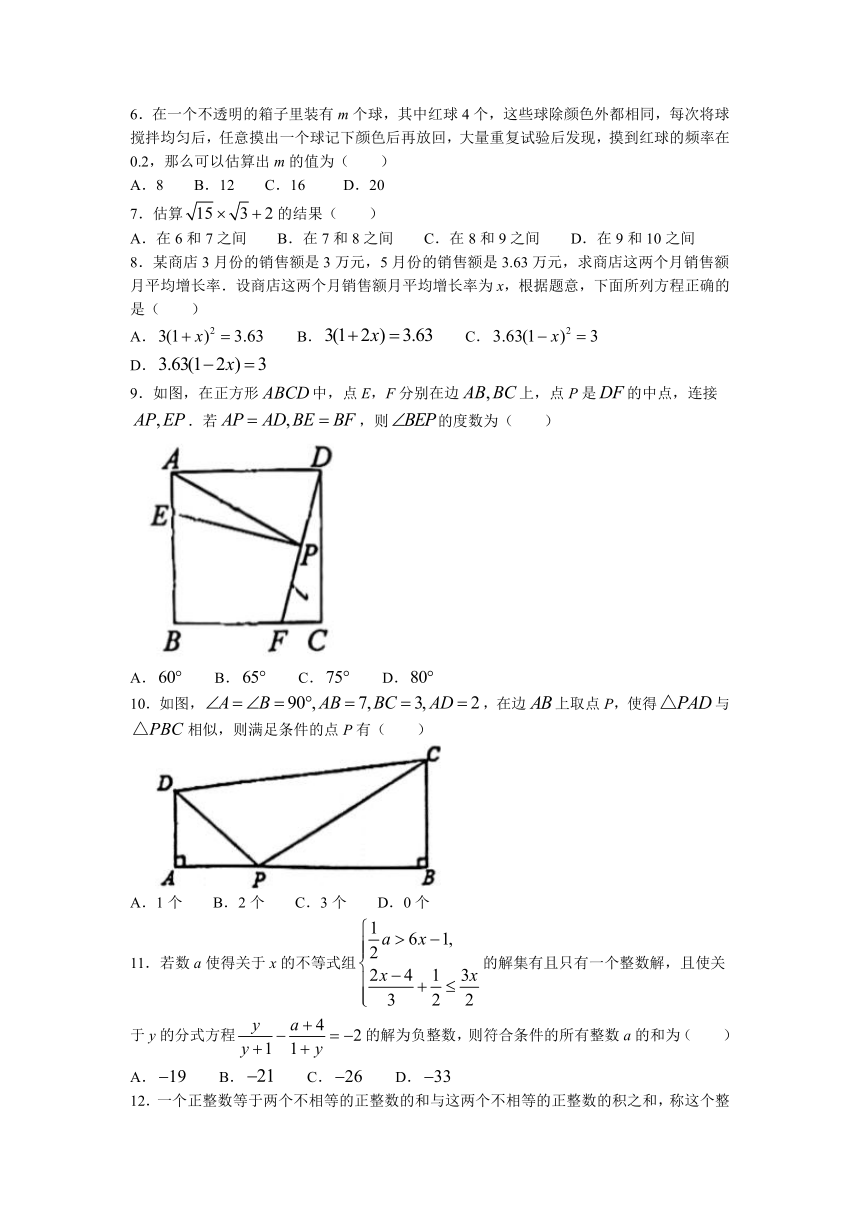
9.如图,在正方形中,点E,F分别在边上,点P是的中点,连接.若,则的度数为( )
A. B. C. D.
10.如图,,在边上取点P,使得与相似,则满足条件的点P有( )
A.1个 B.2个 C.3个 D.0个
11.若数a使得关于x的不等式组的解集有且只有一个整数解,且使关于y的分式方程的解为负整数,则符合条件的所有整数a的和为( )
A. B. C. D.
12.一个正整数等于两个不相等的正整数的和与这两个不相等的正整数的积之和,称这个整数为“可拆分”整数,反之则称“不可拆分”整数.例如,,11是一个“可拆分”整数.下列说法:
①最小的“可拆分”整数是5;
②一个“可拆分”整数的拆分方式可以不只有一种;
③最大的“不可拆分”的两位整数是96.
其中正确的个数是( )
A.0 B.1 C.2 D.3
二、填空题:(本大题4个小题,每小题4分,共16分)请将每小题的答案直接填在答题卡中对应的横线上.
13.8的倒数是______________.
14.周末小张和小王去同一个公园跑步.己知公园有A,B,C三个入口,那么他们从同一个入口进入公园的概率是____________.
15.如图,在等腰中,于点D,点P是边上的一个动点,以为边向右,连接,则的最小值为______________.
16.为进一步改善生态环境,村委会决定在甲、乙、丙三座山上种植香樟和红枫.在实际购买时,香樟的价格比预算低,红枫的价格比预算高,香樟购买数量减少了,红枫购买数量与预算保持不变,结果所花费用恰好与预算费用相等,则实际购买香樟的总费用与实际购买红枫的总费用之比为_____________.
三、解答题:(本大题2个小题,每小题8分,共16分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
17.解方程:(1); (2).
18.在数学课上老师提出了如下问题:
如图,,当与满足什么关系时,
小明认为时,他解答这个问题的思路和步骤如下,请根据小明的思路完成下面的作图与填空:
解:用直尺和圆规,在的右侧找一点M,使(只保留作图痕迹).
∵,
∴①_____________
∵
∴②_________,
∵,
∴③__________,
∴④_____________
∴.
所以满足的关系为:当时,.
四、解答题:(本大题7个小题,每小题10分,共0分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
19.为了研究某树苗的生长情况,研究组在甲、乙两个试验基地同时播下树种,同时随机各抽取20株树苗,记录下每株树苗的长度(单位:),进行整理、描述和分析(用x表示树苗长度,数据分成5组:A.;B.;C.;D.;E.,及以上为优等).下面给出了部分信息:
甲试验基地抽取的20株树苗的长度:28,29,32,34,38,40,42,45,46,51,51,52,54,55,55,55,55,57,60,61.
乙试验基地抽出的20株树苗中,A、B、E三个等级的数据个数相同,C组的所有数据是:42,43,46,49,49.
甲、乙两试验基地抽取的树苗长度的统计表
品种 平均数 中位数 众数 E组所占百分比
甲 47 51 a
乙 47 b 56
根据以上信息,解答下列问题:
(1)填空:__________,__________,___________;
(2)根据以上数据,你认为甲、乙两基地哪个基地的树苗好?并说明理由(写出一条理由即可);
(3)请估计2000株乙基地的树苗为优等的树苗株数是多少?
20.已知一次函数的图象与反比例函数的图象交于点.
(1)求一次函数的表达式,并在图中画出这个一次函数的图象;
(2)根据图象,直接写出不等式:的解集;
(3)点C与点关于y轴对称,连接,求的面积.
21.某电商在抖音上对种植成本为20元/千克的葡萄进行直播销售,如果按每千克40元销售,每天可卖出200千克.通过市场调查发现,如果该葡萄售价每千克降低1元,日销售量将增加20千克.
(1)若日利润保持不变,每千克该葡萄售价可降低多少元?
(2)老张的线下水果店也销售同款葡萄,标价为每千克50元.为提高市场竞争力,促进线下销售,老张决定对该葡萄实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?
22.某社区计划利用如图所示的直角墙角(阴影部分,两边足够长),用40米长的篱笆围成一个矩形花园(篱笆只围两边),设米.
(1)若花园的面积为300米,求x的值;
(2)若在直角墙角内点P处有一棵桂花树,且与墙的距离分别是10米,24米,要将这棵树围在矩形花园内(含边界,不考虑树的粗细),则花园的面积能否为400米?若能,求出x的值;若不能,请说明理由.
23.若一个四位数M的个位数字与十位数字的和与它们的差之积恰好是M去掉个位数字与十位数字后得到的两位数,则这个四位数M为“和差数”.
例如:,∵,∴1514是“和差数”.
又如:,∵,∴2526不是“和差数”.
(1)判断2022,2046是否是“和差数”,并说明理由;
(2)一个“和差数”M的千位数字为a,百位数字为b,十位数字为c,个位数字为d,记,且.当均是整数时,来出所有满足条作的M.
24.如图,直线与反比例函数的图象相交于点,与x轴交于点.
(1)求m和k的值.
(2)若点与点O关于直线对称,连接.
①求点P的坐标;
②若点M在反比例函数的图象上,点N在x轴上,以点A,P,M,N为顶点的四边形平行四边形,请直接写出点M的坐标.
25.在中,,将绕点A旋转,得到.
(1)如图1,当时,四边形是什么四边形?并说明理由;
(2)将绕点A由图1的位置开始顺时针旋转,的延长线交直线于点F.
①旋转至如图2,用等式表示与的数量关系,并证明你的结论;
②旋转至如图3,在①的结论下,的延长线交于点H,E为的中点,且直接写出的长.
数学试题
(全卷共三个大题,满分150分,考试时间120分钟)
1.试题卷上各题的答案用钢笔或圆珠笔书写在答题卡上,不得在试题卷上直接作答;
2.答题前认真阅读答题卡上的注意事项:
3.作图(包括作辅助线)请一律用黑色的签字笔完成.
一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上对应题目的正确答案标号涂黑.
1.正方形的边长为,则它的面积为( )
A. B. C. D.
2.下面四个关系式中,y是x的反比例函数的是( )
A. B. C. D.
3.矩形中,,则的长为( )
A.5 B.4 C.3 D.2
4.如图,曲线反映了某地一天气温随时间的变化情况,则这一天的最高温度约为( )
A. B. C. D.
5.如图,与位似,点O为位似中心,,,则的长是( )
A.12 B.10 C.8 D.6
6.在一个不透明的箱子里装有m个球,其中红球4个,这些球除颜色外都相同,每次将球搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验后发现,摸到红球的频率在0.2,那么可以估算出m的值为( )
A.8 B.12 C.16 D.20
7.估算的结果( )
A.在6和7之间 B.在7和8之间 C.在8和9之间 D.在9和10之间
8.某商店3月份的销售额是3万元,5月份的销售额是3.63万元,求商店这两个月销售额月平均增长率.设商店这两个月销售额月平均增长率为x,根据题意,下面所列方程正确的是( )
A. B. C. D.
9.如图,在正方形中,点E,F分别在边上,点P是的中点,连接.若,则的度数为( )
A. B. C. D.
10.如图,,在边上取点P,使得与相似,则满足条件的点P有( )
A.1个 B.2个 C.3个 D.0个
11.若数a使得关于x的不等式组的解集有且只有一个整数解,且使关于y的分式方程的解为负整数,则符合条件的所有整数a的和为( )
A. B. C. D.
12.一个正整数等于两个不相等的正整数的和与这两个不相等的正整数的积之和,称这个整数为“可拆分”整数,反之则称“不可拆分”整数.例如,,11是一个“可拆分”整数.下列说法:
①最小的“可拆分”整数是5;
②一个“可拆分”整数的拆分方式可以不只有一种;
③最大的“不可拆分”的两位整数是96.
其中正确的个数是( )
A.0 B.1 C.2 D.3
二、填空题:(本大题4个小题,每小题4分,共16分)请将每小题的答案直接填在答题卡中对应的横线上.
13.8的倒数是______________.
14.周末小张和小王去同一个公园跑步.己知公园有A,B,C三个入口,那么他们从同一个入口进入公园的概率是____________.
15.如图,在等腰中,于点D,点P是边上的一个动点,以为边向右,连接,则的最小值为______________.
16.为进一步改善生态环境,村委会决定在甲、乙、丙三座山上种植香樟和红枫.在实际购买时,香樟的价格比预算低,红枫的价格比预算高,香樟购买数量减少了,红枫购买数量与预算保持不变,结果所花费用恰好与预算费用相等,则实际购买香樟的总费用与实际购买红枫的总费用之比为_____________.
三、解答题:(本大题2个小题,每小题8分,共16分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
17.解方程:(1); (2).
18.在数学课上老师提出了如下问题:
如图,,当与满足什么关系时,
小明认为时,他解答这个问题的思路和步骤如下,请根据小明的思路完成下面的作图与填空:
解:用直尺和圆规,在的右侧找一点M,使(只保留作图痕迹).
∵,
∴①_____________
∵
∴②_________,
∵,
∴③__________,
∴④_____________
∴.
所以满足的关系为:当时,.
四、解答题:(本大题7个小题,每小题10分,共0分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
19.为了研究某树苗的生长情况,研究组在甲、乙两个试验基地同时播下树种,同时随机各抽取20株树苗,记录下每株树苗的长度(单位:),进行整理、描述和分析(用x表示树苗长度,数据分成5组:A.;B.;C.;D.;E.,及以上为优等).下面给出了部分信息:
甲试验基地抽取的20株树苗的长度:28,29,32,34,38,40,42,45,46,51,51,52,54,55,55,55,55,57,60,61.
乙试验基地抽出的20株树苗中,A、B、E三个等级的数据个数相同,C组的所有数据是:42,43,46,49,49.
甲、乙两试验基地抽取的树苗长度的统计表
品种 平均数 中位数 众数 E组所占百分比
甲 47 51 a
乙 47 b 56
根据以上信息,解答下列问题:
(1)填空:__________,__________,___________;
(2)根据以上数据,你认为甲、乙两基地哪个基地的树苗好?并说明理由(写出一条理由即可);
(3)请估计2000株乙基地的树苗为优等的树苗株数是多少?
20.已知一次函数的图象与反比例函数的图象交于点.
(1)求一次函数的表达式,并在图中画出这个一次函数的图象;
(2)根据图象,直接写出不等式:的解集;
(3)点C与点关于y轴对称,连接,求的面积.
21.某电商在抖音上对种植成本为20元/千克的葡萄进行直播销售,如果按每千克40元销售,每天可卖出200千克.通过市场调查发现,如果该葡萄售价每千克降低1元,日销售量将增加20千克.
(1)若日利润保持不变,每千克该葡萄售价可降低多少元?
(2)老张的线下水果店也销售同款葡萄,标价为每千克50元.为提高市场竞争力,促进线下销售,老张决定对该葡萄实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?
22.某社区计划利用如图所示的直角墙角(阴影部分,两边足够长),用40米长的篱笆围成一个矩形花园(篱笆只围两边),设米.
(1)若花园的面积为300米,求x的值;
(2)若在直角墙角内点P处有一棵桂花树,且与墙的距离分别是10米,24米,要将这棵树围在矩形花园内(含边界,不考虑树的粗细),则花园的面积能否为400米?若能,求出x的值;若不能,请说明理由.
23.若一个四位数M的个位数字与十位数字的和与它们的差之积恰好是M去掉个位数字与十位数字后得到的两位数,则这个四位数M为“和差数”.
例如:,∵,∴1514是“和差数”.
又如:,∵,∴2526不是“和差数”.
(1)判断2022,2046是否是“和差数”,并说明理由;
(2)一个“和差数”M的千位数字为a,百位数字为b,十位数字为c,个位数字为d,记,且.当均是整数时,来出所有满足条作的M.
24.如图,直线与反比例函数的图象相交于点,与x轴交于点.
(1)求m和k的值.
(2)若点与点O关于直线对称,连接.
①求点P的坐标;
②若点M在反比例函数的图象上,点N在x轴上,以点A,P,M,N为顶点的四边形平行四边形,请直接写出点M的坐标.
25.在中,,将绕点A旋转,得到.
(1)如图1,当时,四边形是什么四边形?并说明理由;
(2)将绕点A由图1的位置开始顺时针旋转,的延长线交直线于点F.
①旋转至如图2,用等式表示与的数量关系,并证明你的结论;
②旋转至如图3,在①的结论下,的延长线交于点H,E为的中点,且直接写出的长.
同课章节目录
