立体几何中球的内切和外接问题 课件(共64张PPT)
文档属性
| 名称 | 立体几何中球的内切和外接问题 课件(共64张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-16 06:40:21 | ||
图片预览




文档简介
(共64张PPT)
类型:内切球、棱切球、外接球
几何体相切:
一个几何体各个面分别与另一个几
何体各个面相切。
与球有关的接切问题
几何体棱切:
一个几何体各个面分别与另一个几
何体各条棱相切。
几何体外接:
一个几何体所有顶点都在另一个几
何体表面上。
二、球与多面体的接、切
定义1:若一个多面体的各顶点都在一个球的球面上, 则称这个多面体是这个球的内接多面体, 这个球是这个 。
定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体, 这个球是这个 。
一、
球体的体积与表面积
①
②
多面体的外接球
多面体的内切球
若棱长为3的正方体的顶点都在同一球面上,
则该球的表面积为 .
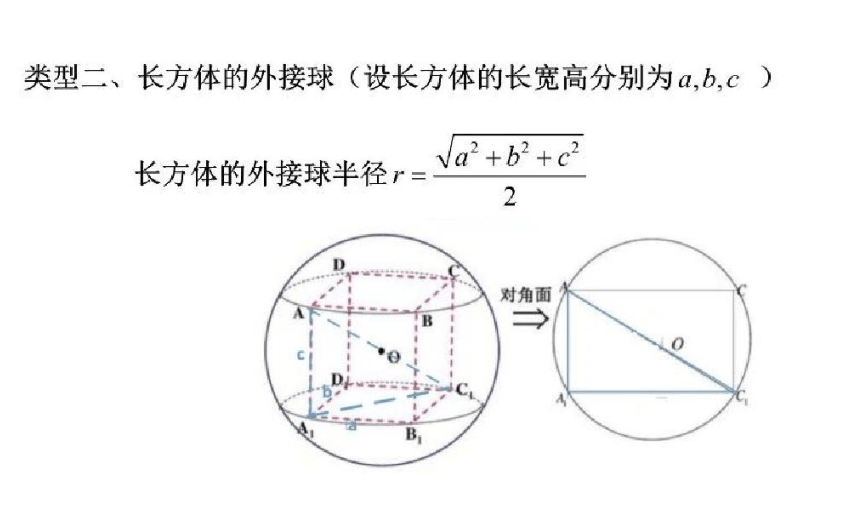
一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3 ,则此球的表面积为 .
A
中截面
设棱长为1
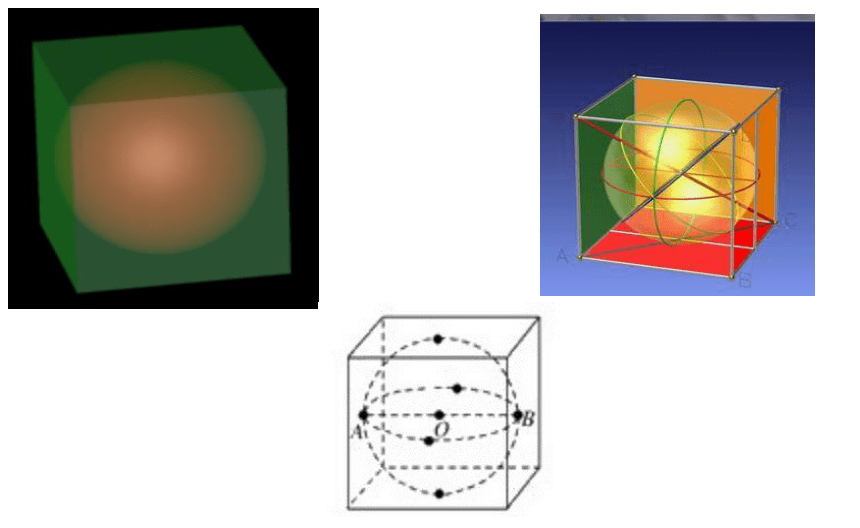
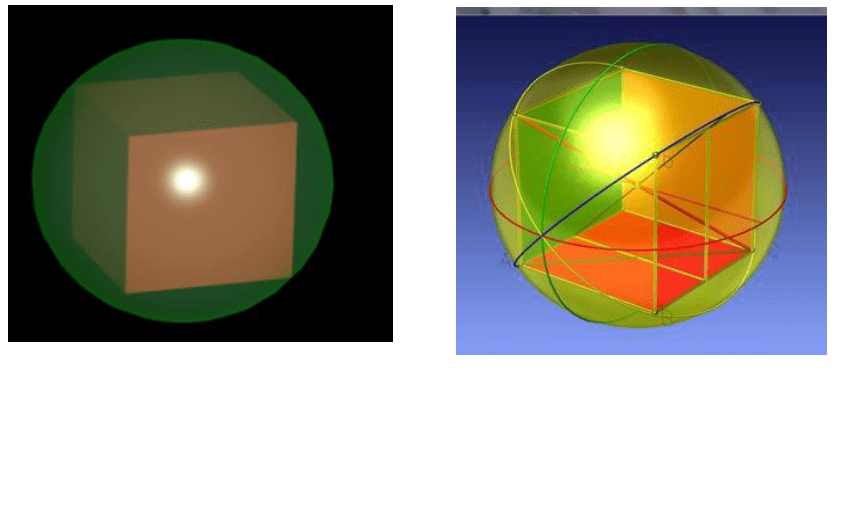
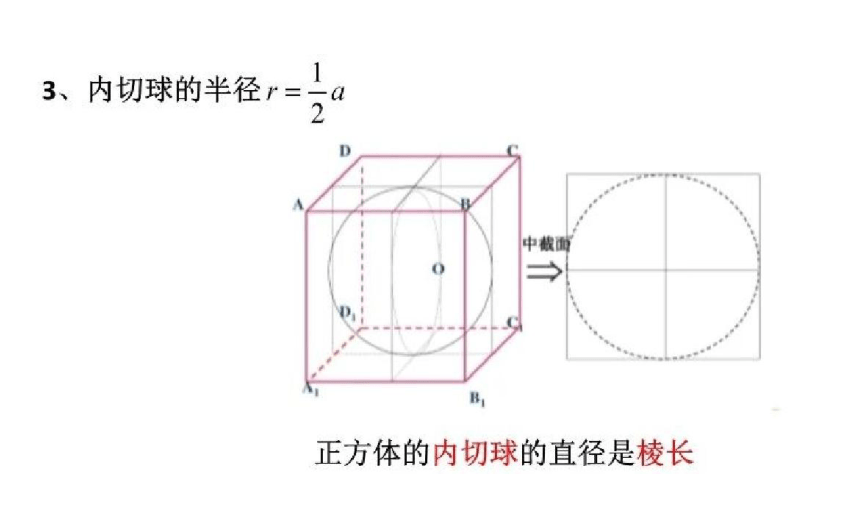
正方体的内切球直径等于棱长。
A
B
C
D
D1
C1
B1
A1
O
甲球内切于正方体的各面,乙球内切于该正方体的各条棱, 丙球外接于该正方体,则三球表面面积之比为( ) A. 1:2:3 B. C. D.
A
B
C
D
D1
C1
B1
A1
O
中截面
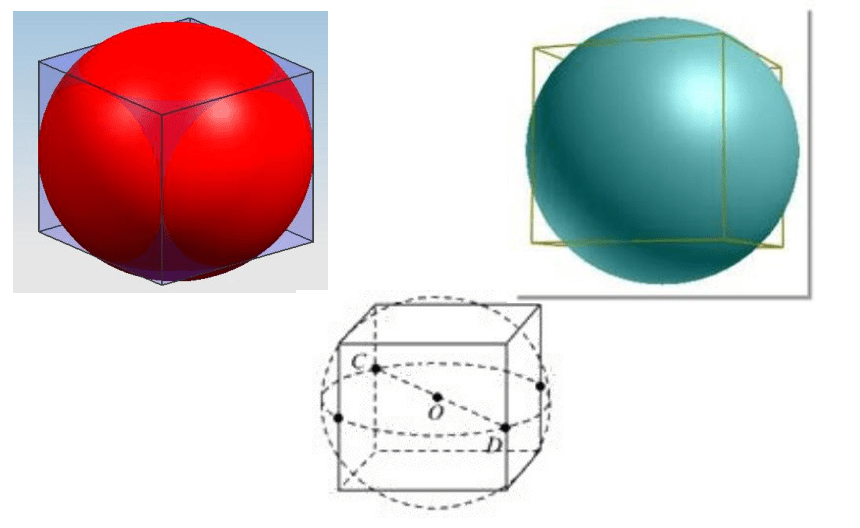
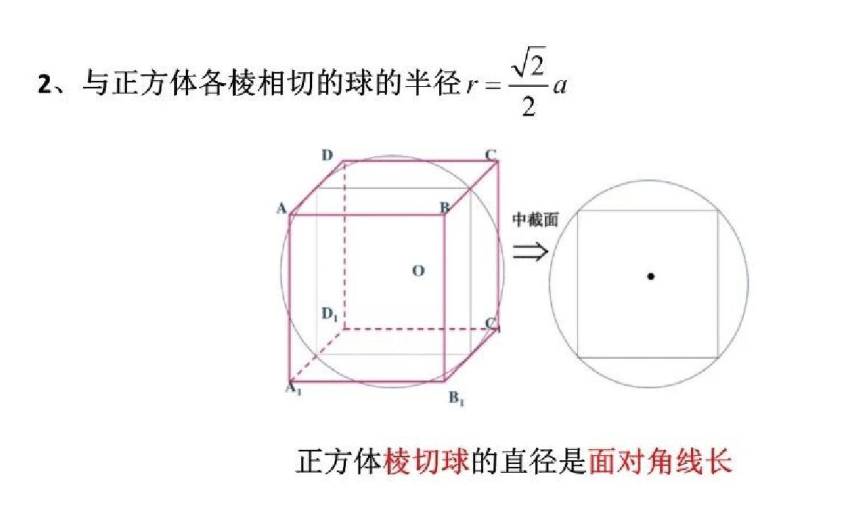
球与正方体棱相切:球的直径等于正方形的面对角线。
.
球内切于正方体的棱
设棱长为1
A
B
C
D
D1
C1
A1
O
B1
对角面
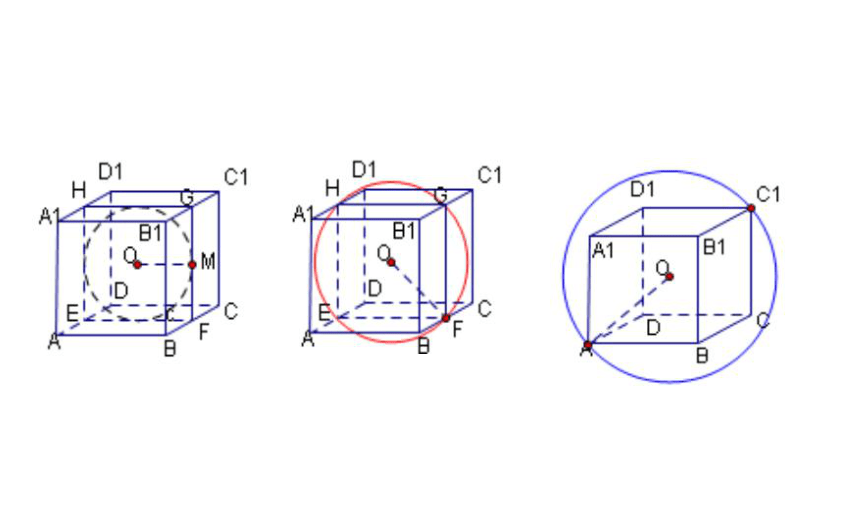
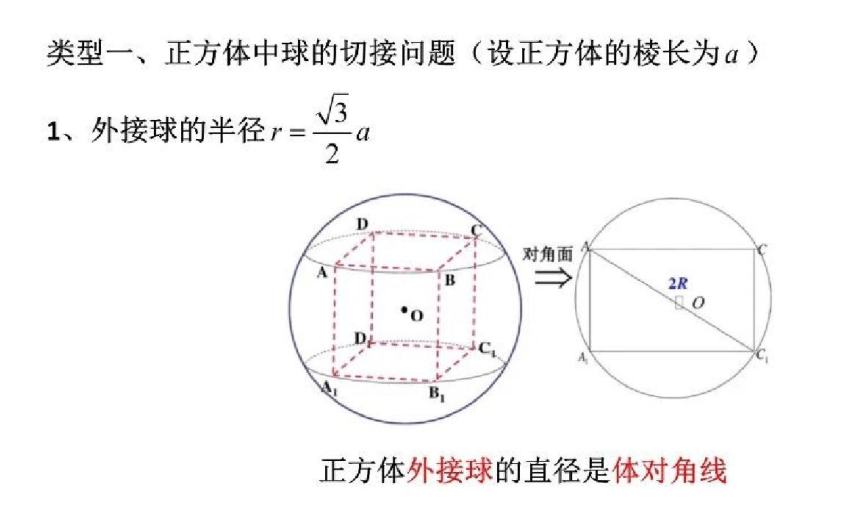
正方体外接球直径是体对角线。
正方体外接球
设棱长为1
A
C
B
P
O
若三棱锥的三条侧棱两两垂直, 且侧棱长均为 ,则其外接球的表面积是
A
B
C
D
O
A
B
C
D
O
求正多面体外接球的半径
求正方体外接球的半径
一个四面体的所有棱长都为 ,四个顶点在同一球面上,则此球的表面积为( )
A. B. C. D.
A
A
B
C
D
O
A
B
C
D
O
求棱长为1的正四面体外接球的体积.
C
A
O
D
B
求棱长为a的正四面体内切球的体积.
正三角形ABC的边长为 ,将它沿高AD翻折,使点B 与点C间的距离为 ,此时四面体ABCD的外接球的体积为 。
等边三角形
某几何体的三视图如图,该几何体的顶点都在球O 的球面上,球O的表面积是 ( )
C
四棱锥P—ABCD,底面ABCD是边长为6的正方形,且PA = PB = PC = PD,若一个半径为1的球与此四棱锥的各个面相切,则此四棱锥的体积为( )
A.15 B.24 C.27 D.30
正视图
侧视图
俯视图
A
A
C
类型:内切球、棱切球、外接球
几何体相切:
一个几何体各个面分别与另一个几
何体各个面相切。
与球有关的接切问题
几何体棱切:
一个几何体各个面分别与另一个几
何体各条棱相切。
几何体外接:
一个几何体所有顶点都在另一个几
何体表面上。
二、球与多面体的接、切
定义1:若一个多面体的各顶点都在一个球的球面上, 则称这个多面体是这个球的内接多面体, 这个球是这个 。
定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体, 这个球是这个 。
一、
球体的体积与表面积
①
②
多面体的外接球
多面体的内切球
若棱长为3的正方体的顶点都在同一球面上,
则该球的表面积为 .
一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3 ,则此球的表面积为 .
A
中截面
设棱长为1
正方体的内切球直径等于棱长。
A
B
C
D
D1
C1
B1
A1
O
甲球内切于正方体的各面,乙球内切于该正方体的各条棱, 丙球外接于该正方体,则三球表面面积之比为( ) A. 1:2:3 B. C. D.
A
B
C
D
D1
C1
B1
A1
O
中截面
球与正方体棱相切:球的直径等于正方形的面对角线。
.
球内切于正方体的棱
设棱长为1
A
B
C
D
D1
C1
A1
O
B1
对角面
正方体外接球直径是体对角线。
正方体外接球
设棱长为1
A
C
B
P
O
若三棱锥的三条侧棱两两垂直, 且侧棱长均为 ,则其外接球的表面积是
A
B
C
D
O
A
B
C
D
O
求正多面体外接球的半径
求正方体外接球的半径
一个四面体的所有棱长都为 ,四个顶点在同一球面上,则此球的表面积为( )
A. B. C. D.
A
A
B
C
D
O
A
B
C
D
O
求棱长为1的正四面体外接球的体积.
C
A
O
D
B
求棱长为a的正四面体内切球的体积.
正三角形ABC的边长为 ,将它沿高AD翻折,使点B 与点C间的距离为 ,此时四面体ABCD的外接球的体积为 。
等边三角形
某几何体的三视图如图,该几何体的顶点都在球O 的球面上,球O的表面积是 ( )
C
四棱锥P—ABCD,底面ABCD是边长为6的正方形,且PA = PB = PC = PD,若一个半径为1的球与此四棱锥的各个面相切,则此四棱锥的体积为( )
A.15 B.24 C.27 D.30
正视图
侧视图
俯视图
A
A
C
同课章节目录
