安徽省滁州市定远县育才学校2022-2023学年九年级下学期3月月考数学试题(含解析)
文档属性
| 名称 | 安徽省滁州市定远县育才学校2022-2023学年九年级下学期3月月考数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 240.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-16 23:09:14 | ||
图片预览




文档简介
定远育才学校2022-2023学年度第二学期3月考试
九年级数学试题
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、选择题(本大题共10小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 的相反数是( )
A. B. C. D.
2. 下列运算正确的是( )
A. B.
C. D.
3. 中国华为麒麟处理器是采用纳米制程工艺的手机芯片,在的尺寸上塞进了亿个晶体管,是世界上最先进的具有人工智能的手机处理,亿用科学记数法表示为( )
A. B. C. D.
4. 由个相同的小正方体组成的几何体如图所示,从正面看该几何体得到的平面图形是( )
A. B.
C. D.
5. 若关于的分式方程的解是负数,则的取值范围为( )
A. 且 B.
C. 且 D.
6. 如图,将钝角绕点按逆时针方向旋转,得到,连接,若,则的大小为( )
A. B. C. D.
7. 本学期某校举行了四次数学测试,李娜同学四次的成绩单位:分分别为,,,,王玥同学四次的成绩分别为,,,,且李娜同学四次成绩的中位数比王玥同学四次成绩的中位数少分,则下列说法正确的是( )
A. 的值为
B. 两位同学成绩的平均数相同
C. 李娜同学成绩的众数比王玥同学成绩的众数大
D. 王玥同学的成绩比李娜同学的成绩稳定
8. 某轮船在静水中的速度为,水流速度为,该船从甲码头顺流航行到乙码头,再返回甲码头,共用时不计停留时间,设甲、乙两码头之间的距离为,则可列方程为( )
A. B.
C. D.
9. 如图,在中,以点为圆心,适当长度为半径画弧,分别交、于点、再分别以点、为圆心,大于的长为半径画弧.两弧交于点作射线交边于点过点作于点,若,,,则的长度为( )
A.
B.
C.
D.
10. 如图是抛物线的一部分,抛物线的顶点坐标是,与轴的一个交点是,点在抛物线上,且在直线上方,则下列结论正确的是( )
A.
B. 方程有两个相等的实数根
C.
D. 点到直线的最大距离
二、填空题(本大题共4小题,共20分)
11. 因式分______.
12. 如图,半径为的两个等圆,外切于点,切于点,弦,连接,,则图中阴影部分的面积等于______结果保留
13. 如图,、是第二象限内双曲线上的点,、两点的横坐标分别是、,线段的延长线交轴于点,若,则的值为______ .
14. 如图,在矩形中,,点为射线上一点,且,点为的中点,连接,,将沿直线折叠,若点的对应点恰好落在上,则的长为______.
三、解答题(本大题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤)
15. 本小题分
计算:;
化简:.
16. 本小题分
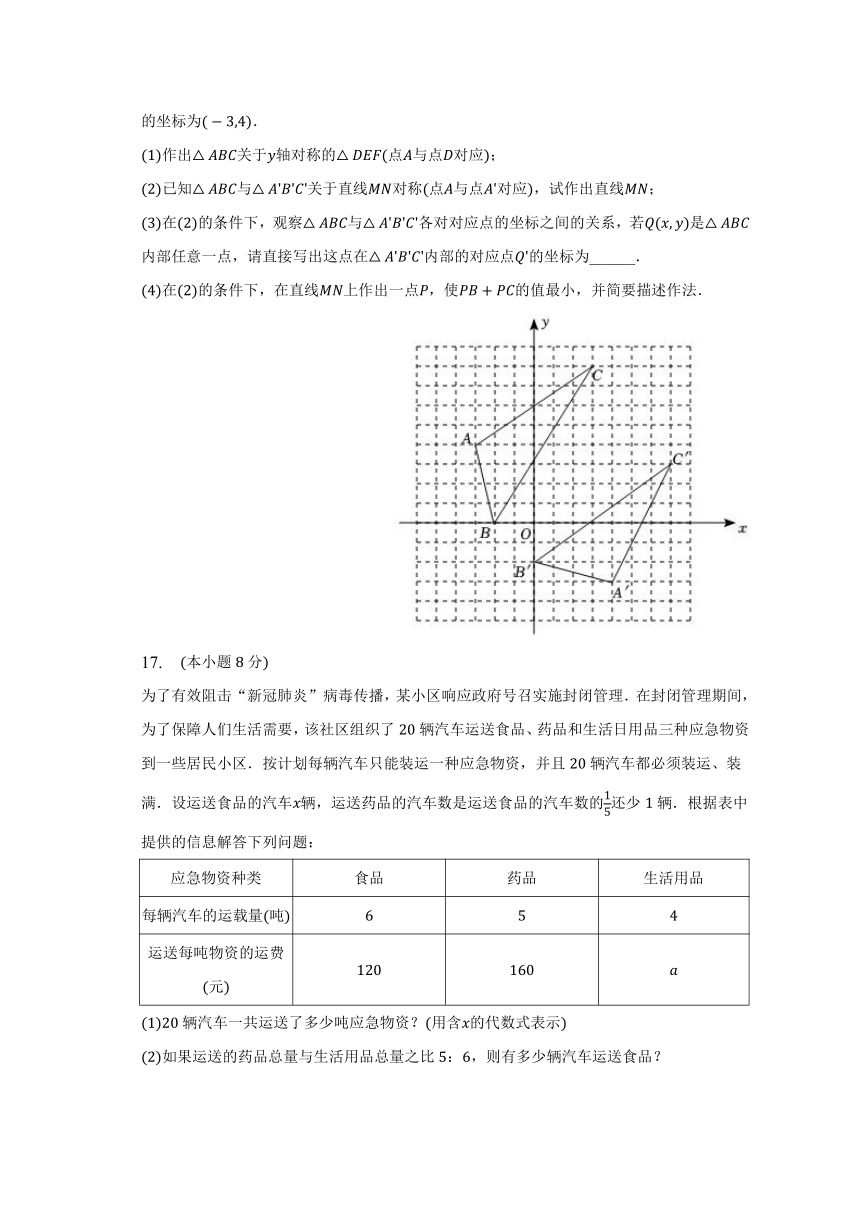
如图,在下列带有坐标系的网格中,的顶点都在边长为的小正方形的顶点上,且点的坐标为.
作出关于轴对称的点与点对应;
已知与关于直线对称点与点对应,试作出直线;
在的条件下,观察与各对对应点的坐标之间的关系,若是内部任意一点,请直接写出这点在内部的对应点的坐标为______.
在的条件下,在直线上作出一点,使的值最小,并简要描述作法.
17. 本小题分
为了有效阻击“新冠肺炎”病毒传播,某小区响应政府号召实施封闭管理.在封闭管理期间,为了保障人们生活需要,该社区组织了辆汽车运送食品、药品和生活日用品三种应急物资到一些居民小区.按计划每辆汽车只能装运一种应急物资,并且辆汽车都必须装运、装满.设运送食品的汽车辆,运送药品的汽车数是运送食品的汽车数的还少辆.根据表中提供的信息解答下列问题:
应急物资种类 食品 药品 生活用品
每辆汽车的运载量吨
运送每吨物资的运费元
辆汽车一共运送了多少吨应急物资?用含的代数式表示
如果运送的药品总量与生活用品总量之比:,则有多少辆汽车运送食品?
在的条件下,若运送这批应急物资所需要的总运费是元,则运送吨生活用品的运费是多少元?
18. 本小题分
新修订的未成年人保护法是一部全方位保障未成年人权益的综合性、基础性法律某中学为了让学生学习并进行测试,现分别从七、八两个年级各随机抽取名学生的测试成绩分,并对其统计、整理如下:
七年级名学生测试成绩扇形统计图如下,其测试成绩在之间的是:、、、、;
八年级名同学测试成绩统计如下:、、、、、、、、、;
两个年级测试成绩的平均数、中位数、众数如表:
统计量 平均数 中位数 众数
七年级
八年级
根据以信息,回答下列问题:
填空:______;______;
若该校八年级共有年学生,请根据上述调查结果估计八年级测试成绩在之间的人数;
已知七年教本次测试成绩中排在前四名的学生是名男生和名女生,若从他们中任选两人作为代表进行普法演讲,试求恰好选中两个男生的概率.
19. 本小题分
如图,、是两个核酸检测点,点、、是附近的在同一条直线上的三个小区的物业服务中心,在处测得点在正北处,点在北偏东,在处测得点在北偏东,点在北偏西,,求、两个小区的物业服务中心距离.结果保留整数,参考数据:
20. 本小题分
阅读下列材料:
,,,,,
.
解答下列问题:
在和式中,第项为______,第项是______.
上述求和的想法是:将和式中的各分数转化为两数之差,使得除首末两项外的中间各项可以抵消,从而达到求和的目的,受此启发,请你解下面的方程:.
21. 本小题分
如图,是的外接圆,是的直径,是延长线上一点,连接,,且.
求证:是的切线;
若,,求的长.
22. 本小题分
如图,抛物线与轴交于、两点,与轴交于点,且,直线与抛物线交于、两点,与轴交于点,点是抛物线的顶点,设直线上方抛物线上的动点的横坐标为.
求该抛物线的解析式及顶点的坐标;
连接、,当为何值时,;
在直线上是否存在一点使为等腰直角三角形,若存在请直接写出点的坐标,不存在请说明理由.
23. 本小题分
已知为等边三角形,点、分别是、上一点.
如图,,连接、,交于点,在的延长线上取点,使得,连接,若,求的面积;
如图,、相交于点,点为延长线上一点,连接、、,已知,,,探究、、之间的数量关系并说明理由;
如图,已知,过点作于点,点是直线上一点,以为边,在的下方作等边,连,当取最小值时请直接写出的长.
答案和解析
1. 【解析】的相反数是,故选:.
2. 【解析】,故选项A错误,不符合题意;
,故选项B错误,不符合题意;
,故选项C正确,符合题意;
,故选项D错误,不符合题意;故选:.
3. 【解析】亿.故选:.
4. 【解析】这个组合体从正面看到的图形如下:
故选:.
5. 【解析】分式方程去分母得:,
整理得:,
移项合并得:,
解得:,
分式方程的解为负数,
且,
解得:且.故选:.
6. 【解析】由旋转的性质可得,,
,
,
,
,故A正确.故选:.
7. 【解析】李娜同学四次的成绩的中位数为分,
由题意知王玥同学四次的成绩的中位数为分,
则分,故A选项错误;
李娜成绩的平均数为分,王玥成绩的平均数为分,故B选项错误;
李娜同学成绩的众数为分,王玥同学成绩的众数为分,故C选项错误;
王玥同学的成绩的方差为,
李娜同学的成绩的方差为,
王玥同学的成绩比李娜同学的成绩稳定,故D选项正确;故选:.
8. 【解析】由题意得,
,故选D.
9.
【解析】如图,延长交的延长线于点,作于点,于点,
,,,
,,
,
,
设,则,
由作图可知平分,
,,
,
,
,
,
在中,,
,
,
故选:.
10. 【解析】由图象可知开口向下,
,
函数与轴的交点在轴的正半轴上,
,
对称轴为直线,
,
,
故A不符合题意;
抛物线的顶点坐标是,
时,方程的解为,
方程有且只有一个实数根,
故B不符合题意;
当时,,
,即,
故C符合题意;
设直线的解析式为,
,
解得,
,
设抛物线,将点代入,
,
解得,
,
过点作轴交于点,
设点坐标为,则,
,
当时,的面积有最大值,
,
,
点到直线的最大距离,
故D不符合题意;故选:.
11.
【解析】原式
.故答案为:.
12.
【解析】连接,,
,,
,,,
是正三角形
阴影部分的面积.
13.
【解析】分别过点、作轴于点,轴于点,轴于点,轴于点,
反比例函数的图象在第二象限,
,
点是反比例函数图象上的点,
,
、两点的横坐标分别是、,
,
点是的二等分点,
,,
,解得,
故答案为:.
14.或
【解析】分两种情况:
设,
当在边上时,如图,连接,则,
四边形是矩形,
,,
,,
,
由折叠得:,,,
点为的中点,
,
,
,
在和中
≌,
,
,
,
,
;
当点在的延长线上时,如图,连接,则,
,
,
,
,
综上,的长是或.
15.
;
.
16.
【解析】如图所示,即为所求;
如图所示,直线即为所求;
点;故答案为:;
如图所示,连接或交直线于点,则点即为所求.
17.由题意可知,运送药品的汽车有辆,则运送生活日用品的汽车有辆,
辆汽车一共运送的应急物资有:
吨,
辆汽车一共运送了吨应急物资;
依题意有:::,
解得.
故有辆汽车运送食品;
当时,一共运送的应急物资为:
吨,
运送这批应急物资的总费用是:
依题意有:,
解得.
故运送吨生活用品的运费是元.
18.
【解析】的人数为人,的人数为人,
七年级中位数在中,
由题意知七年级中位数,
八年级众数,
故答案为:,;
估计八年级测试成绩在之间的人数为人;
列表如下:
男 男 男 女
男 男,男 男,男 女,男
男 男,男 男,男 女,男
男 男,男 男,男 女,男
女 男,女 男,女 男,女
由表知,共有种等可能结果,其中恰好选中两个男生的有种结果,
所以恰好选中两个男生的概率为.
19.如图,
过作于点,过作于点,
则四边形是矩形,
,,
由题意得:,,,
是等腰直角三角形,
,
在中,,,
,,
,,
,
在中,,,
,
,
,
答:、两个小区的物业服务中心距离约为.
20. ;
【解析】,
故答案为:;;
将分式方程变形为,
整理得,方程两边都乘以,
得,
解得.
经检验,是原分式方程的根.
21.连接,
是的直径,
,
,
又,
,
又.
,
,
即,
是的切线;
,,
,
在中,
,,
,
,
,
,,
∽,
,
设,则,,
又,
即,
解得或舍去,
.
22.,,
点的坐标为,点的坐标为,
设抛物线的表达式为,将点的坐标代入,得,
解得,
抛物线的表达式为,
,
抛物线的顶点坐标为:.
联立,
解得:,,
点的坐标为,
如图,过点作轴的平行线,交于点,设点,则点,
,
解得:或.
存在;
设点,点,,而点,
当时,如图,过点作轴的平行线,过点,点作轴的平行线,交过点且平行于轴的直线于点,,
,,
,
,,
≌,
,,
即,,
解得:或,
当时,,解得,舍去
点;
当时,如图所示,
此时,则点、关于抛物线对称轴对称,即垂直抛物线的对称轴,而对称轴与轴垂直,故轴,则,
同理可得,舍去,
故点坐标为.
当时,
Ⅰ当点在抛物线对称轴右侧时,如图所示:
点在下方,与题意不符,故舍去;
Ⅱ当点在抛物线对称轴左侧时,同理可得,
解得:舍去,,
点;
综上可得,点的坐标为或.
23.是等边三角形,
,,
又,
≌,
,
,
又,
是等边三角形,
;
,理由如下:
由可知:≌,,,
又,
是等边三角形,
,,
,
又,
≌,
,
,
,,
,,
≌,
,
,
,
;
如图,连接,
是等边三角形,,
,,,,
是等边三角形,
,,
,
≌,
,,
点在过点且与成度的直线上移动,
当时,有最小值,
此时,的最小值,
,
,
,
.
九年级数学试题
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、选择题(本大题共10小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 的相反数是( )
A. B. C. D.
2. 下列运算正确的是( )
A. B.
C. D.
3. 中国华为麒麟处理器是采用纳米制程工艺的手机芯片,在的尺寸上塞进了亿个晶体管,是世界上最先进的具有人工智能的手机处理,亿用科学记数法表示为( )
A. B. C. D.
4. 由个相同的小正方体组成的几何体如图所示,从正面看该几何体得到的平面图形是( )
A. B.
C. D.
5. 若关于的分式方程的解是负数,则的取值范围为( )
A. 且 B.
C. 且 D.
6. 如图,将钝角绕点按逆时针方向旋转,得到,连接,若,则的大小为( )
A. B. C. D.
7. 本学期某校举行了四次数学测试,李娜同学四次的成绩单位:分分别为,,,,王玥同学四次的成绩分别为,,,,且李娜同学四次成绩的中位数比王玥同学四次成绩的中位数少分,则下列说法正确的是( )
A. 的值为
B. 两位同学成绩的平均数相同
C. 李娜同学成绩的众数比王玥同学成绩的众数大
D. 王玥同学的成绩比李娜同学的成绩稳定
8. 某轮船在静水中的速度为,水流速度为,该船从甲码头顺流航行到乙码头,再返回甲码头,共用时不计停留时间,设甲、乙两码头之间的距离为,则可列方程为( )
A. B.
C. D.
9. 如图,在中,以点为圆心,适当长度为半径画弧,分别交、于点、再分别以点、为圆心,大于的长为半径画弧.两弧交于点作射线交边于点过点作于点,若,,,则的长度为( )
A.
B.
C.
D.
10. 如图是抛物线的一部分,抛物线的顶点坐标是,与轴的一个交点是,点在抛物线上,且在直线上方,则下列结论正确的是( )
A.
B. 方程有两个相等的实数根
C.
D. 点到直线的最大距离
二、填空题(本大题共4小题,共20分)
11. 因式分______.
12. 如图,半径为的两个等圆,外切于点,切于点,弦,连接,,则图中阴影部分的面积等于______结果保留
13. 如图,、是第二象限内双曲线上的点,、两点的横坐标分别是、,线段的延长线交轴于点,若,则的值为______ .
14. 如图,在矩形中,,点为射线上一点,且,点为的中点,连接,,将沿直线折叠,若点的对应点恰好落在上,则的长为______.
三、解答题(本大题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤)
15. 本小题分
计算:;
化简:.
16. 本小题分
如图,在下列带有坐标系的网格中,的顶点都在边长为的小正方形的顶点上,且点的坐标为.
作出关于轴对称的点与点对应;
已知与关于直线对称点与点对应,试作出直线;
在的条件下,观察与各对对应点的坐标之间的关系,若是内部任意一点,请直接写出这点在内部的对应点的坐标为______.
在的条件下,在直线上作出一点,使的值最小,并简要描述作法.
17. 本小题分
为了有效阻击“新冠肺炎”病毒传播,某小区响应政府号召实施封闭管理.在封闭管理期间,为了保障人们生活需要,该社区组织了辆汽车运送食品、药品和生活日用品三种应急物资到一些居民小区.按计划每辆汽车只能装运一种应急物资,并且辆汽车都必须装运、装满.设运送食品的汽车辆,运送药品的汽车数是运送食品的汽车数的还少辆.根据表中提供的信息解答下列问题:
应急物资种类 食品 药品 生活用品
每辆汽车的运载量吨
运送每吨物资的运费元
辆汽车一共运送了多少吨应急物资?用含的代数式表示
如果运送的药品总量与生活用品总量之比:,则有多少辆汽车运送食品?
在的条件下,若运送这批应急物资所需要的总运费是元,则运送吨生活用品的运费是多少元?
18. 本小题分
新修订的未成年人保护法是一部全方位保障未成年人权益的综合性、基础性法律某中学为了让学生学习并进行测试,现分别从七、八两个年级各随机抽取名学生的测试成绩分,并对其统计、整理如下:
七年级名学生测试成绩扇形统计图如下,其测试成绩在之间的是:、、、、;
八年级名同学测试成绩统计如下:、、、、、、、、、;
两个年级测试成绩的平均数、中位数、众数如表:
统计量 平均数 中位数 众数
七年级
八年级
根据以信息,回答下列问题:
填空:______;______;
若该校八年级共有年学生,请根据上述调查结果估计八年级测试成绩在之间的人数;
已知七年教本次测试成绩中排在前四名的学生是名男生和名女生,若从他们中任选两人作为代表进行普法演讲,试求恰好选中两个男生的概率.
19. 本小题分
如图,、是两个核酸检测点,点、、是附近的在同一条直线上的三个小区的物业服务中心,在处测得点在正北处,点在北偏东,在处测得点在北偏东,点在北偏西,,求、两个小区的物业服务中心距离.结果保留整数,参考数据:
20. 本小题分
阅读下列材料:
,,,,,
.
解答下列问题:
在和式中,第项为______,第项是______.
上述求和的想法是:将和式中的各分数转化为两数之差,使得除首末两项外的中间各项可以抵消,从而达到求和的目的,受此启发,请你解下面的方程:.
21. 本小题分
如图,是的外接圆,是的直径,是延长线上一点,连接,,且.
求证:是的切线;
若,,求的长.
22. 本小题分
如图,抛物线与轴交于、两点,与轴交于点,且,直线与抛物线交于、两点,与轴交于点,点是抛物线的顶点,设直线上方抛物线上的动点的横坐标为.
求该抛物线的解析式及顶点的坐标;
连接、,当为何值时,;
在直线上是否存在一点使为等腰直角三角形,若存在请直接写出点的坐标,不存在请说明理由.
23. 本小题分
已知为等边三角形,点、分别是、上一点.
如图,,连接、,交于点,在的延长线上取点,使得,连接,若,求的面积;
如图,、相交于点,点为延长线上一点,连接、、,已知,,,探究、、之间的数量关系并说明理由;
如图,已知,过点作于点,点是直线上一点,以为边,在的下方作等边,连,当取最小值时请直接写出的长.
答案和解析
1. 【解析】的相反数是,故选:.
2. 【解析】,故选项A错误,不符合题意;
,故选项B错误,不符合题意;
,故选项C正确,符合题意;
,故选项D错误,不符合题意;故选:.
3. 【解析】亿.故选:.
4. 【解析】这个组合体从正面看到的图形如下:
故选:.
5. 【解析】分式方程去分母得:,
整理得:,
移项合并得:,
解得:,
分式方程的解为负数,
且,
解得:且.故选:.
6. 【解析】由旋转的性质可得,,
,
,
,
,故A正确.故选:.
7. 【解析】李娜同学四次的成绩的中位数为分,
由题意知王玥同学四次的成绩的中位数为分,
则分,故A选项错误;
李娜成绩的平均数为分,王玥成绩的平均数为分,故B选项错误;
李娜同学成绩的众数为分,王玥同学成绩的众数为分,故C选项错误;
王玥同学的成绩的方差为,
李娜同学的成绩的方差为,
王玥同学的成绩比李娜同学的成绩稳定,故D选项正确;故选:.
8. 【解析】由题意得,
,故选D.
9.
【解析】如图,延长交的延长线于点,作于点,于点,
,,,
,,
,
,
设,则,
由作图可知平分,
,,
,
,
,
,
在中,,
,
,
故选:.
10. 【解析】由图象可知开口向下,
,
函数与轴的交点在轴的正半轴上,
,
对称轴为直线,
,
,
故A不符合题意;
抛物线的顶点坐标是,
时,方程的解为,
方程有且只有一个实数根,
故B不符合题意;
当时,,
,即,
故C符合题意;
设直线的解析式为,
,
解得,
,
设抛物线,将点代入,
,
解得,
,
过点作轴交于点,
设点坐标为,则,
,
当时,的面积有最大值,
,
,
点到直线的最大距离,
故D不符合题意;故选:.
11.
【解析】原式
.故答案为:.
12.
【解析】连接,,
,,
,,,
是正三角形
阴影部分的面积.
13.
【解析】分别过点、作轴于点,轴于点,轴于点,轴于点,
反比例函数的图象在第二象限,
,
点是反比例函数图象上的点,
,
、两点的横坐标分别是、,
,
点是的二等分点,
,,
,解得,
故答案为:.
14.或
【解析】分两种情况:
设,
当在边上时,如图,连接,则,
四边形是矩形,
,,
,,
,
由折叠得:,,,
点为的中点,
,
,
,
在和中
≌,
,
,
,
,
;
当点在的延长线上时,如图,连接,则,
,
,
,
,
综上,的长是或.
15.
;
.
16.
【解析】如图所示,即为所求;
如图所示,直线即为所求;
点;故答案为:;
如图所示,连接或交直线于点,则点即为所求.
17.由题意可知,运送药品的汽车有辆,则运送生活日用品的汽车有辆,
辆汽车一共运送的应急物资有:
吨,
辆汽车一共运送了吨应急物资;
依题意有:::,
解得.
故有辆汽车运送食品;
当时,一共运送的应急物资为:
吨,
运送这批应急物资的总费用是:
依题意有:,
解得.
故运送吨生活用品的运费是元.
18.
【解析】的人数为人,的人数为人,
七年级中位数在中,
由题意知七年级中位数,
八年级众数,
故答案为:,;
估计八年级测试成绩在之间的人数为人;
列表如下:
男 男 男 女
男 男,男 男,男 女,男
男 男,男 男,男 女,男
男 男,男 男,男 女,男
女 男,女 男,女 男,女
由表知,共有种等可能结果,其中恰好选中两个男生的有种结果,
所以恰好选中两个男生的概率为.
19.如图,
过作于点,过作于点,
则四边形是矩形,
,,
由题意得:,,,
是等腰直角三角形,
,
在中,,,
,,
,,
,
在中,,,
,
,
,
答:、两个小区的物业服务中心距离约为.
20. ;
【解析】,
故答案为:;;
将分式方程变形为,
整理得,方程两边都乘以,
得,
解得.
经检验,是原分式方程的根.
21.连接,
是的直径,
,
,
又,
,
又.
,
,
即,
是的切线;
,,
,
在中,
,,
,
,
,
,,
∽,
,
设,则,,
又,
即,
解得或舍去,
.
22.,,
点的坐标为,点的坐标为,
设抛物线的表达式为,将点的坐标代入,得,
解得,
抛物线的表达式为,
,
抛物线的顶点坐标为:.
联立,
解得:,,
点的坐标为,
如图,过点作轴的平行线,交于点,设点,则点,
,
解得:或.
存在;
设点,点,,而点,
当时,如图,过点作轴的平行线,过点,点作轴的平行线,交过点且平行于轴的直线于点,,
,,
,
,,
≌,
,,
即,,
解得:或,
当时,,解得,舍去
点;
当时,如图所示,
此时,则点、关于抛物线对称轴对称,即垂直抛物线的对称轴,而对称轴与轴垂直,故轴,则,
同理可得,舍去,
故点坐标为.
当时,
Ⅰ当点在抛物线对称轴右侧时,如图所示:
点在下方,与题意不符,故舍去;
Ⅱ当点在抛物线对称轴左侧时,同理可得,
解得:舍去,,
点;
综上可得,点的坐标为或.
23.是等边三角形,
,,
又,
≌,
,
,
又,
是等边三角形,
;
,理由如下:
由可知:≌,,,
又,
是等边三角形,
,,
,
又,
≌,
,
,
,,
,,
≌,
,
,
,
;
如图,连接,
是等边三角形,,
,,,,
是等边三角形,
,,
,
≌,
,,
点在过点且与成度的直线上移动,
当时,有最小值,
此时,的最小值,
,
,
,
.
同课章节目录
