2023年高考数学复习专题课件★★立体几何中的综合问题 课件(共38张PPT)
文档属性
| 名称 | 2023年高考数学复习专题课件★★立体几何中的综合问题 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 14:35:32 | ||
图片预览










文档简介
(共38张PPT)
2023年高考数学发展专题课件★★立体几何中的综合问题
命题点(一) 立体几何中的折叠问题
对立体几何中的折叠问题,要求学生要有较强的空间想象力和准确的计算运算能力,才能顺利解答.从实际教学和考试来看,学生对这类题看到就头疼.分析原因,首先是学生的空间想象力较弱,其次是学生对这类问题没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理.
[关键点拨]
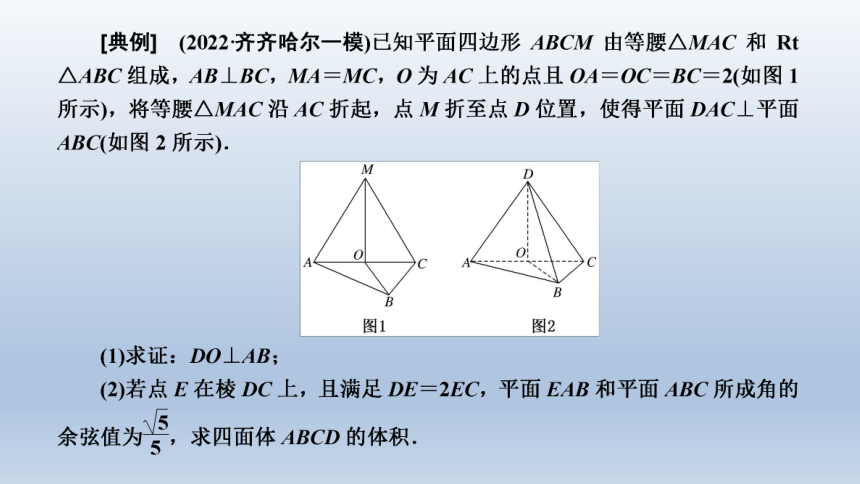
切入点 通过面面垂直的性质证明DO⊥平面ABC,进而证明DO⊥AB
迁移点 建立坐标系,写出两个平面的法向量,通过锐二面角的余弦值求出参数,进而计算四面体ABCD的体积
[解] (1)证明:因为MA=MC,OA=OC,
所以在△ACD中,DO⊥AC.
又因为平面DAC⊥平面ABC,平面DAC∩平面ABC=AC,DO 平面DAC,
所以DO⊥平面ABC,
又因为AB 平面ABC,
所以DO⊥AB.
画好翻折前后的平面图形与立体图形,分清翻折前后图形的位置和数量关系的变与不变.一般地,位于“折痕”同侧的点、线、面之间的位置和数量关系不变,而位于“折痕”两侧的点、线、面之间的位置关系会发生变化;对于不变的关系应在平面图形中处理,而对于变化的关系则要在立体图形中解决.
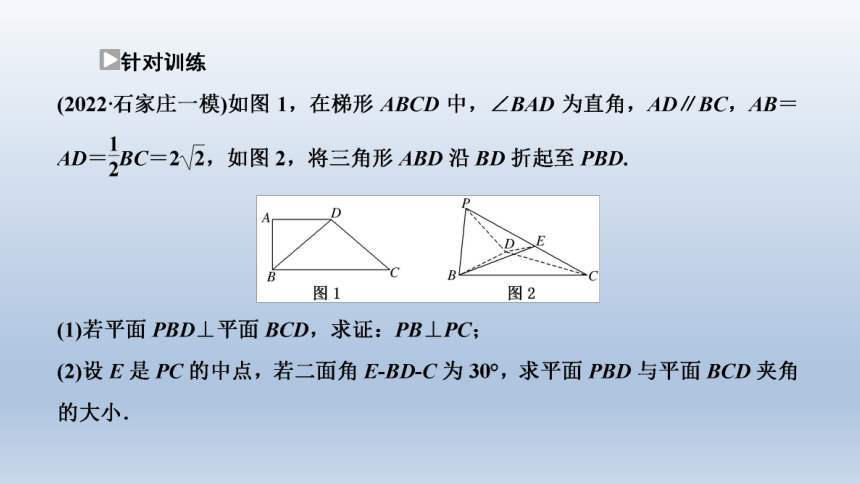
(2)设M,N分别是BD,BC的中点,连接PM,MN,则PM⊥BD,MN⊥BD,
又PM∩MN=M,
则BD⊥平面PMN,
所以∠PMN是二面角P-BD-C的平面角.
在平面PMN上过M作Mz⊥MN,
如图,以M为原点,直线MB为x轴,直线MN为y轴,直线Mz为
z轴,建立空间直角坐标系.
则B(2,0,0),C(-2,4,0),
D(-2,0,0),设∠PMN=θ,θ∈(0,π),
命题点(二) 立体几何中的探究性问题
与空间向量有关的探究性问题主要有两类:一类是探究线面的位置关系;另一类是探究线面角或两平面的夹角满足特定要求时的存在性问题.处理原则:先建立空间直角坐标系,引入参数(有些是题中已给出),设出关键点的坐标,然后探究这样的点是否存在,或参数是否满足要求,从而作出判断.
[典例] (2022·济南期末)如图,在正四棱柱ABCD-A1B1C1D1中,
AA1=2AB=2,E,F,分别为棱AA1,CC1的中点,G为棱DD1上的
动点.
(1)求证:B,E,D1,F四点共面;
(2)是否存在点G,使得平面GEF⊥平面BEF?若存在,求出DG的长度;若不存在,说明理由.
[关键点拨]
切入点 以D为坐标原点,DA,DC,DD1分别为x轴,y轴,z轴建立空间直角坐标系
迁移点 假设存在满足题意的点G,根据题意列方程求解
[解] (1)证明:如图所示.
连接D1E,D1F,取BB1的中点为M,连接MC1,ME,
因为E为AA1的中点,所以EM∥A1B1∥C1D1,且EM=A1B1=
C1D1,
所以四边形EMC1D1为平行四边形,
所以D1E∥MC1,
又因为F为CC1的中点,
所以BM∥C1F,且BM=C1F,
所以四边形BMC1F为平行四边形,
所以BF∥MC1,
所以BF∥D1E,
所以B,E,D1,F四点共面.
解决立体几何中探索性问题的基本方法
(1)通常假设问题中的数学对象存在或结论成立,再在这个前提下进行推理,如果能推出与条件吻合的数据或事实,说明假设成立,并可进一步证明,否则假设不成立.
(2)探索线段上是否存在满足条件的点时,一定注意三点共线的条件的应用.
解:(1)证明:因为FC∥PE,FC 平面A′PE,PE 平面A′PE,所以FC∥平面A′PE.
因为平面A′PE⊥平面ABC,平面A′PE∩平面ABC=PE,且A′E⊥PE,A′E 平面A′PE,所以A′E⊥平面ABC,
同理,B′F⊥平面ABC,所以B′F∥A′E,因为A′E 平面A′PE,所以B′F∥平面A′PE.
又B′F,FC均在平面B′CF内,B′F∩FC=F,所以平面B′CF∥平面A′PE,从而B′C∥平面A′PE.
命题点(三) 立体几何中的最值问题
立体几何中的最值问题主要有三类,一是距离(长度)的最值问题;二是面(体)积的最值问题;三是在最值已知的条件下,确定参数(其他几何量)的值.从解答思路看,有几何法(利用几何特征)和代数法(应用函数思想、基本不等式等)两种,这两种解答思路都需要我们正确揭示空间图形与平面图形的联系,并有效地实施空间图形与平面图形的转换.要善于将空间问题转化为平面问题,这一步要求我们具备较强的空间想象能力,熟练掌握几何体的结构特征及有关计算公式.
[解] (1)证明:在正三棱柱ABC-A1B1C1中,
因为D,E分别为BC,B1C1的中点,所以EC1綊BD,
所以四边形BDC1E为平行四边形,所以BE∥DC1,
又因为BE 平面C1DA,DC1 平面C1DA,所以BE∥平面C1DA,同理可证A1E∥平面C1DA,
因为A1E∩BE=E,A1E,BE 平面BA1E,所以平面BA1E∥平面C1DA.
角度与距离取值范围问题的求解策略
极端化 在考察空间几何体中的运动对象时,直接考虑它的极端情形,如它的起点位置与终点位置,从中得出一般性的结论,从而达到解决问题的目的
函数化 将所有待解决的立体几何中的最值问题通过代数化转化为一个变量或多个变量的函数问题,运用函数求最值的方法来解决立体几何中的最值问题.此外,用变量表示出立体几何待求的问题后,也常用均值不等式的方法加以解决.立体几何问题的函数化,常用方法是建立平面直角坐标系或空间直角坐标系,用坐标中的变量表示几何对象的变化
答案:C
2.(2022·枣庄三模)如图,在平行六面体ABCD-A1B1C1D1中,A1D
⊥底面ABCD,AB=AA1=2AD=2,∠DAB=60°.
(1)证明:AD⊥A1B;
(2)设点P为线段DC1上一点(异于D,C1),当DP为何值时,平面A1PB与平面AA1D1D夹角的余弦值最大?
“课时验收评价”见“课时验收评价(四)”
(单击进入电子文档)
2023年高考数学发展专题课件★★立体几何中的综合问题
命题点(一) 立体几何中的折叠问题
对立体几何中的折叠问题,要求学生要有较强的空间想象力和准确的计算运算能力,才能顺利解答.从实际教学和考试来看,学生对这类题看到就头疼.分析原因,首先是学生的空间想象力较弱,其次是学生对这类问题没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理.
[关键点拨]
切入点 通过面面垂直的性质证明DO⊥平面ABC,进而证明DO⊥AB
迁移点 建立坐标系,写出两个平面的法向量,通过锐二面角的余弦值求出参数,进而计算四面体ABCD的体积
[解] (1)证明:因为MA=MC,OA=OC,
所以在△ACD中,DO⊥AC.
又因为平面DAC⊥平面ABC,平面DAC∩平面ABC=AC,DO 平面DAC,
所以DO⊥平面ABC,
又因为AB 平面ABC,
所以DO⊥AB.
画好翻折前后的平面图形与立体图形,分清翻折前后图形的位置和数量关系的变与不变.一般地,位于“折痕”同侧的点、线、面之间的位置和数量关系不变,而位于“折痕”两侧的点、线、面之间的位置关系会发生变化;对于不变的关系应在平面图形中处理,而对于变化的关系则要在立体图形中解决.
(2)设M,N分别是BD,BC的中点,连接PM,MN,则PM⊥BD,MN⊥BD,
又PM∩MN=M,
则BD⊥平面PMN,
所以∠PMN是二面角P-BD-C的平面角.
在平面PMN上过M作Mz⊥MN,
如图,以M为原点,直线MB为x轴,直线MN为y轴,直线Mz为
z轴,建立空间直角坐标系.
则B(2,0,0),C(-2,4,0),
D(-2,0,0),设∠PMN=θ,θ∈(0,π),
命题点(二) 立体几何中的探究性问题
与空间向量有关的探究性问题主要有两类:一类是探究线面的位置关系;另一类是探究线面角或两平面的夹角满足特定要求时的存在性问题.处理原则:先建立空间直角坐标系,引入参数(有些是题中已给出),设出关键点的坐标,然后探究这样的点是否存在,或参数是否满足要求,从而作出判断.
[典例] (2022·济南期末)如图,在正四棱柱ABCD-A1B1C1D1中,
AA1=2AB=2,E,F,分别为棱AA1,CC1的中点,G为棱DD1上的
动点.
(1)求证:B,E,D1,F四点共面;
(2)是否存在点G,使得平面GEF⊥平面BEF?若存在,求出DG的长度;若不存在,说明理由.
[关键点拨]
切入点 以D为坐标原点,DA,DC,DD1分别为x轴,y轴,z轴建立空间直角坐标系
迁移点 假设存在满足题意的点G,根据题意列方程求解
[解] (1)证明:如图所示.
连接D1E,D1F,取BB1的中点为M,连接MC1,ME,
因为E为AA1的中点,所以EM∥A1B1∥C1D1,且EM=A1B1=
C1D1,
所以四边形EMC1D1为平行四边形,
所以D1E∥MC1,
又因为F为CC1的中点,
所以BM∥C1F,且BM=C1F,
所以四边形BMC1F为平行四边形,
所以BF∥MC1,
所以BF∥D1E,
所以B,E,D1,F四点共面.
解决立体几何中探索性问题的基本方法
(1)通常假设问题中的数学对象存在或结论成立,再在这个前提下进行推理,如果能推出与条件吻合的数据或事实,说明假设成立,并可进一步证明,否则假设不成立.
(2)探索线段上是否存在满足条件的点时,一定注意三点共线的条件的应用.
解:(1)证明:因为FC∥PE,FC 平面A′PE,PE 平面A′PE,所以FC∥平面A′PE.
因为平面A′PE⊥平面ABC,平面A′PE∩平面ABC=PE,且A′E⊥PE,A′E 平面A′PE,所以A′E⊥平面ABC,
同理,B′F⊥平面ABC,所以B′F∥A′E,因为A′E 平面A′PE,所以B′F∥平面A′PE.
又B′F,FC均在平面B′CF内,B′F∩FC=F,所以平面B′CF∥平面A′PE,从而B′C∥平面A′PE.
命题点(三) 立体几何中的最值问题
立体几何中的最值问题主要有三类,一是距离(长度)的最值问题;二是面(体)积的最值问题;三是在最值已知的条件下,确定参数(其他几何量)的值.从解答思路看,有几何法(利用几何特征)和代数法(应用函数思想、基本不等式等)两种,这两种解答思路都需要我们正确揭示空间图形与平面图形的联系,并有效地实施空间图形与平面图形的转换.要善于将空间问题转化为平面问题,这一步要求我们具备较强的空间想象能力,熟练掌握几何体的结构特征及有关计算公式.
[解] (1)证明:在正三棱柱ABC-A1B1C1中,
因为D,E分别为BC,B1C1的中点,所以EC1綊BD,
所以四边形BDC1E为平行四边形,所以BE∥DC1,
又因为BE 平面C1DA,DC1 平面C1DA,所以BE∥平面C1DA,同理可证A1E∥平面C1DA,
因为A1E∩BE=E,A1E,BE 平面BA1E,所以平面BA1E∥平面C1DA.
角度与距离取值范围问题的求解策略
极端化 在考察空间几何体中的运动对象时,直接考虑它的极端情形,如它的起点位置与终点位置,从中得出一般性的结论,从而达到解决问题的目的
函数化 将所有待解决的立体几何中的最值问题通过代数化转化为一个变量或多个变量的函数问题,运用函数求最值的方法来解决立体几何中的最值问题.此外,用变量表示出立体几何待求的问题后,也常用均值不等式的方法加以解决.立体几何问题的函数化,常用方法是建立平面直角坐标系或空间直角坐标系,用坐标中的变量表示几何对象的变化
答案:C
2.(2022·枣庄三模)如图,在平行六面体ABCD-A1B1C1D1中,A1D
⊥底面ABCD,AB=AA1=2AD=2,∠DAB=60°.
(1)证明:AD⊥A1B;
(2)设点P为线段DC1上一点(异于D,C1),当DP为何值时,平面A1PB与平面AA1D1D夹角的余弦值最大?
“课时验收评价”见“课时验收评价(四)”
(单击进入电子文档)
同课章节目录
