2023年高考数学复习专题课件★★解析几何中的最值与范围、探索性问题 课件(共30张PPT)
文档属性
| 名称 | 2023年高考数学复习专题课件★★解析几何中的最值与范围、探索性问题 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 598.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 14:37:00 | ||
图片预览




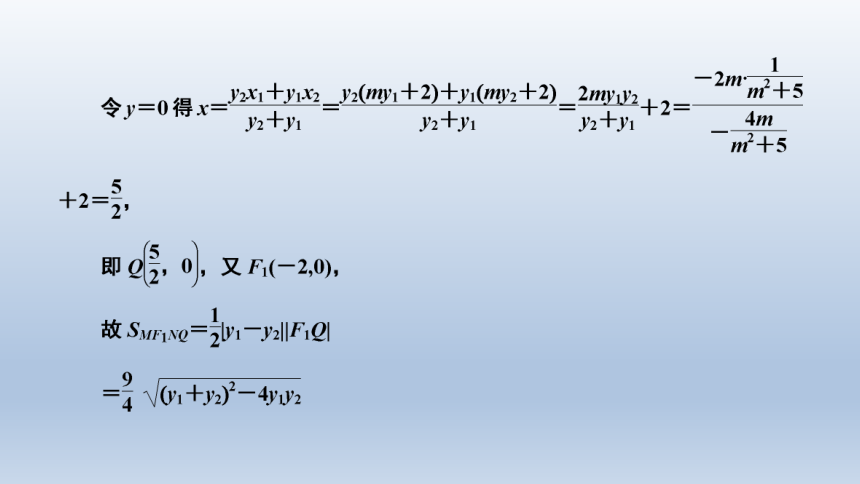




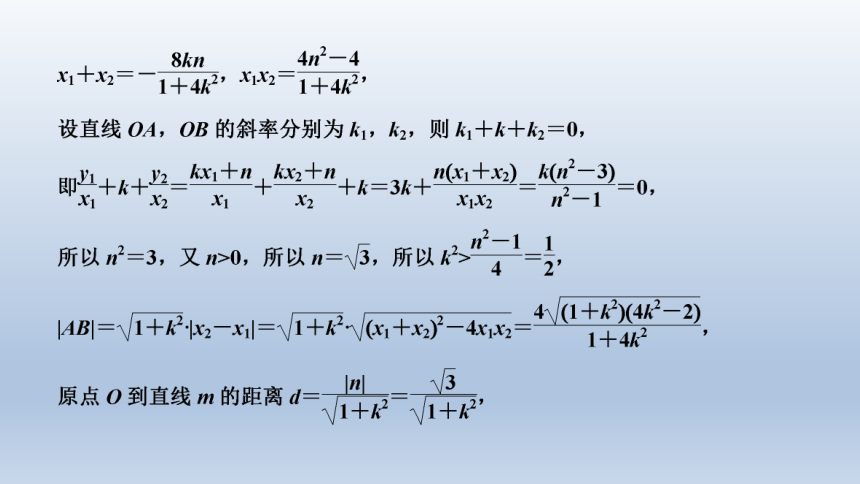


文档简介
(共30张PPT)
2023年高考数学复习专题课件★★
解析几何中的最值与范围、探索性问题
命题点(一) 最值与范围问题
求解范围、最值问题的常见方法?
(1)利用判别式来构造不等关系.?
(2)利用已知参数的范围,在两个参数之间建立函数关系.?
(3)利用隐含或已知的不等关系建立不等式.?
(4)利用基本不等式.
求四边形面积的最值,首先分割,借助三角形面积转化为函数的最值问题;求解最值应用了两个技巧:一是换元,运用函数的性质;二是利用已知或隐含的不等关系构造不等式求解.
圆锥曲线中求解含双变量的式子的取值范围的方法:几何条件定代换,目标关系式求范围.
一般分三步完成:第一步,消参,将直线l的方程与圆锥曲线的方程联立,得两个变量的等量关系 (此时需要检验判别式Δ>0);
第二步,将等量关系代入目标关系式;
第三步,利用函数的性质求取值范围.
命题点(二) 探索性问题
解决探索性问题,先假设存在,推证满足条件的结论,若结论正确则存在,若结论不正确则不存在.?
(1)当条件和结论不唯一时要分类讨论.?
(2)当给出结论而要推导出存在的条件时,先假设成立,再推出条件.?
(3)当要讨论的量能够确定时,可先确定,再证明结论符合题意.
探索性问题的求解步骤:假设满足条件的元素(点、直线、曲线或参数)存在,用待定系数法设出,列出关于待定系数的方程组,若方程组有实数解,则元素(点、直线、曲线或参数)存在,否则,元素(点、直线、曲线或参数)不存在.
2023年高考数学复习专题课件★★
解析几何中的最值与范围、探索性问题
命题点(一) 最值与范围问题
求解范围、最值问题的常见方法?
(1)利用判别式来构造不等关系.?
(2)利用已知参数的范围,在两个参数之间建立函数关系.?
(3)利用隐含或已知的不等关系建立不等式.?
(4)利用基本不等式.
求四边形面积的最值,首先分割,借助三角形面积转化为函数的最值问题;求解最值应用了两个技巧:一是换元,运用函数的性质;二是利用已知或隐含的不等关系构造不等式求解.
圆锥曲线中求解含双变量的式子的取值范围的方法:几何条件定代换,目标关系式求范围.
一般分三步完成:第一步,消参,将直线l的方程与圆锥曲线的方程联立,得两个变量的等量关系 (此时需要检验判别式Δ>0);
第二步,将等量关系代入目标关系式;
第三步,利用函数的性质求取值范围.
命题点(二) 探索性问题
解决探索性问题,先假设存在,推证满足条件的结论,若结论正确则存在,若结论不正确则不存在.?
(1)当条件和结论不唯一时要分类讨论.?
(2)当给出结论而要推导出存在的条件时,先假设成立,再推出条件.?
(3)当要讨论的量能够确定时,可先确定,再证明结论符合题意.
探索性问题的求解步骤:假设满足条件的元素(点、直线、曲线或参数)存在,用待定系数法设出,列出关于待定系数的方程组,若方程组有实数解,则元素(点、直线、曲线或参数)存在,否则,元素(点、直线、曲线或参数)不存在.
同课章节目录
