2023届高考数学复习专题★★ 圆锥曲线中的证明与探索性问题 课件(共28张PPT)
文档属性
| 名称 | 2023届高考数学复习专题★★ 圆锥曲线中的证明与探索性问题 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-30 09:04:04 | ||
图片预览





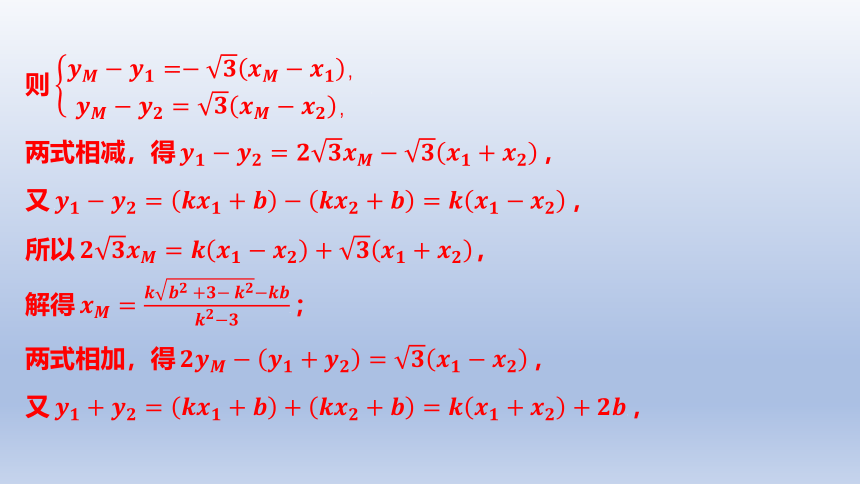



文档简介
(共28张PPT)
圆锥曲线中的证明与探索性问题
2023届高考数学复习专题★★
技法一 代数运算巧证明
【模型解法】
圆锥曲线证明问题,常见的有位置关系和数量关系,位置关系证明有相切、垂直、过定点等;数量关系证明有存在定值、恒成立、值相等、角相等、三点共线等.其解题策略为:
例1 (2022·新高考卷Ⅱ)已知双曲线
(1)求
【解】由题意得
因为双曲线的渐近线方程为
所以
又
所以双曲线
(2)过
①
注:若选择不同的组合分别解答,则按第一个解答计分.
【解】由题意知直线
则
所以
所以
设点
则
两式相减,得
又
所以
解得
两式相加,得
又
所以
解得
因此,点
若选择①②:因为
不妨令点
则由
同理可得
所以
点
得
故
若选择①③:当直线
不在直线
当直线
不妨令点
则由
同理可得
因为
所以
又点
解得
若选择②③:因为
不妨令点
则由
同理可得
设
因为
即点
与
即点
圆锥曲线中证明问题的求解策略
处理圆锥曲线中的证明问题常采用直接法证明,证明时常借助于等价转化思想,化几何关系为数量关系,然后借助函数方程思想、数形结合思想解决.
(2022·高三名校联考信息卷(二))已知动点
(1)求
解:根据抛物线的定义知,点
设
易知抛物线
准线为直线
所以抛物线
(2)过
证明:因为圆
所以圆心
设
则直线
即
(2022·高三名校联考信息卷(二))已知动点
因为直线
整理得
同理可得
所以
所以
又直线
所以圆
所以直线
技法二 假设存在探求存在性
【模型解法】
圆锥曲线中的是否存在问题一般采用假设存在法破解,即先假设所探究的元素存在,在这个假设下探究其是否符合题目中所给信息,从而得到结论.解决问题的策略:
例2 (2022·广东广州综合测试(一))在平面直角坐标系
(1)求
【解】设点
所以
(2)已知点
【解】存在.根据椭圆的对称性,不妨设点
轴的上方.
①当点
由于直线
则直线
所以
②当点
设直线
由
得
得
得
由
直线
直线
因为
所以
综上所述,存在
求解探索性问题的注意点
(1)当条件和结论不唯一时,要分类讨论;
(2)当给出结论而要推导出存在的条件时,先假设成立,再推出条件;
(3)当条件和结论都不确定,按常规方法解题很难时,要开放思维,采取别的合适的方法.
(2022·贵州贵阳五校联考(三))已知椭圆
(1)求椭圆
解:设椭圆
因为过椭圆
所以
所以
故椭圆
(2)是否存在斜率为2的直线
[答案] 假设存在满足条件的直线
设直线
由
所以
故
连接
而
所以
此时点
圆锥曲线中的证明与探索性问题
2023届高考数学复习专题★★
技法一 代数运算巧证明
【模型解法】
圆锥曲线证明问题,常见的有位置关系和数量关系,位置关系证明有相切、垂直、过定点等;数量关系证明有存在定值、恒成立、值相等、角相等、三点共线等.其解题策略为:
例1 (2022·新高考卷Ⅱ)已知双曲线
(1)求
【解】由题意得
因为双曲线的渐近线方程为
所以
又
所以双曲线
(2)过
①
注:若选择不同的组合分别解答,则按第一个解答计分.
【解】由题意知直线
则
所以
所以
设点
则
两式相减,得
又
所以
解得
两式相加,得
又
所以
解得
因此,点
若选择①②:因为
不妨令点
则由
同理可得
所以
点
得
故
若选择①③:当直线
不在直线
当直线
不妨令点
则由
同理可得
因为
所以
又点
解得
若选择②③:因为
不妨令点
则由
同理可得
设
因为
即点
与
即点
圆锥曲线中证明问题的求解策略
处理圆锥曲线中的证明问题常采用直接法证明,证明时常借助于等价转化思想,化几何关系为数量关系,然后借助函数方程思想、数形结合思想解决.
(2022·高三名校联考信息卷(二))已知动点
(1)求
解:根据抛物线的定义知,点
设
易知抛物线
准线为直线
所以抛物线
(2)过
证明:因为圆
所以圆心
设
则直线
即
(2022·高三名校联考信息卷(二))已知动点
因为直线
整理得
同理可得
所以
所以
又直线
所以圆
所以直线
技法二 假设存在探求存在性
【模型解法】
圆锥曲线中的是否存在问题一般采用假设存在法破解,即先假设所探究的元素存在,在这个假设下探究其是否符合题目中所给信息,从而得到结论.解决问题的策略:
例2 (2022·广东广州综合测试(一))在平面直角坐标系
(1)求
【解】设点
所以
(2)已知点
【解】存在.根据椭圆的对称性,不妨设点
轴的上方.
①当点
由于直线
则直线
所以
②当点
设直线
由
得
得
得
由
直线
直线
因为
所以
综上所述,存在
求解探索性问题的注意点
(1)当条件和结论不唯一时,要分类讨论;
(2)当给出结论而要推导出存在的条件时,先假设成立,再推出条件;
(3)当条件和结论都不确定,按常规方法解题很难时,要开放思维,采取别的合适的方法.
(2022·贵州贵阳五校联考(三))已知椭圆
(1)求椭圆
解:设椭圆
因为过椭圆
所以
所以
故椭圆
(2)是否存在斜率为2的直线
[答案] 假设存在满足条件的直线
设直线
由
所以
故
连接
而
所以
此时点
同课章节目录
