广东省深圳市南山外国语集团2022-2023学年九年级下学期三月质量监测数学试卷(无答案)
文档属性
| 名称 | 广东省深圳市南山外国语集团2022-2023学年九年级下学期三月质量监测数学试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-31 14:48:16 | ||
图片预览

文档简介
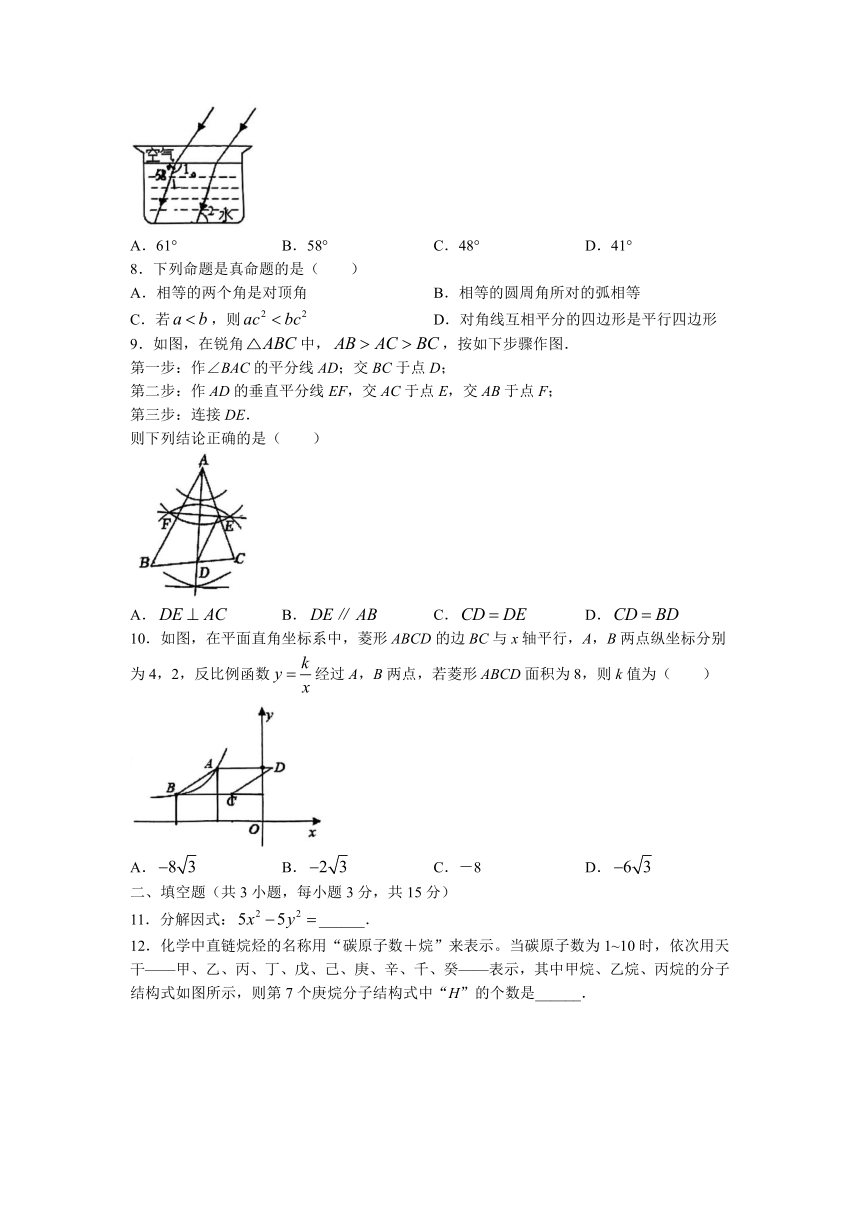
2022-2023学年第二学期三月质量监测
九年级数学试卷
一、选择题(共10小题,每小题3分,共30分)
1.-2023的相反数是( )
A.-2023 B.2023 C. D.
2.2022年4月16日,神舟十三号载人飞船圆满完成全部既定任务,顺利返回地球家园.六个月的飞天之旅展现了中国航天科技的新高度.下列航天图标,其图案是中心对称图形的是( )
A.中国探火 B.中国火箭
C.中国行星探测 D.航天神舟
3.2021年是中国共产党建党百年,走过百年光辉历程的中国共产党,成为世界最大的马克思主义执政党.截止2023年6月5日全国共有9518万名中国共产党员,将“9518万”用科学记数法表示应为( )
A. B. C. D.
4.下列运算正确的是( )
A. B.
C. D.
5.神奇的自然界处处蕴含着数学知识.动物学家在鹦鹉螺外壳上发现,其每圈螺纹的直径与相邻螺纹直径的比约为0.618,这体现了数学中的( )
A.平移 B.旋转 C.轴对称 D.黄金分割
6.某小组长统计组内5人一天在课堂上的发言次数分别为3,3,0,4,5.关于这组数据,下列说法错误的是( )
A.众数是3 B.中位数是0 C.平均数是3 D.极差是5
7.光线在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.如图,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且,则( )
A.61° B.58° C.48° D.41°
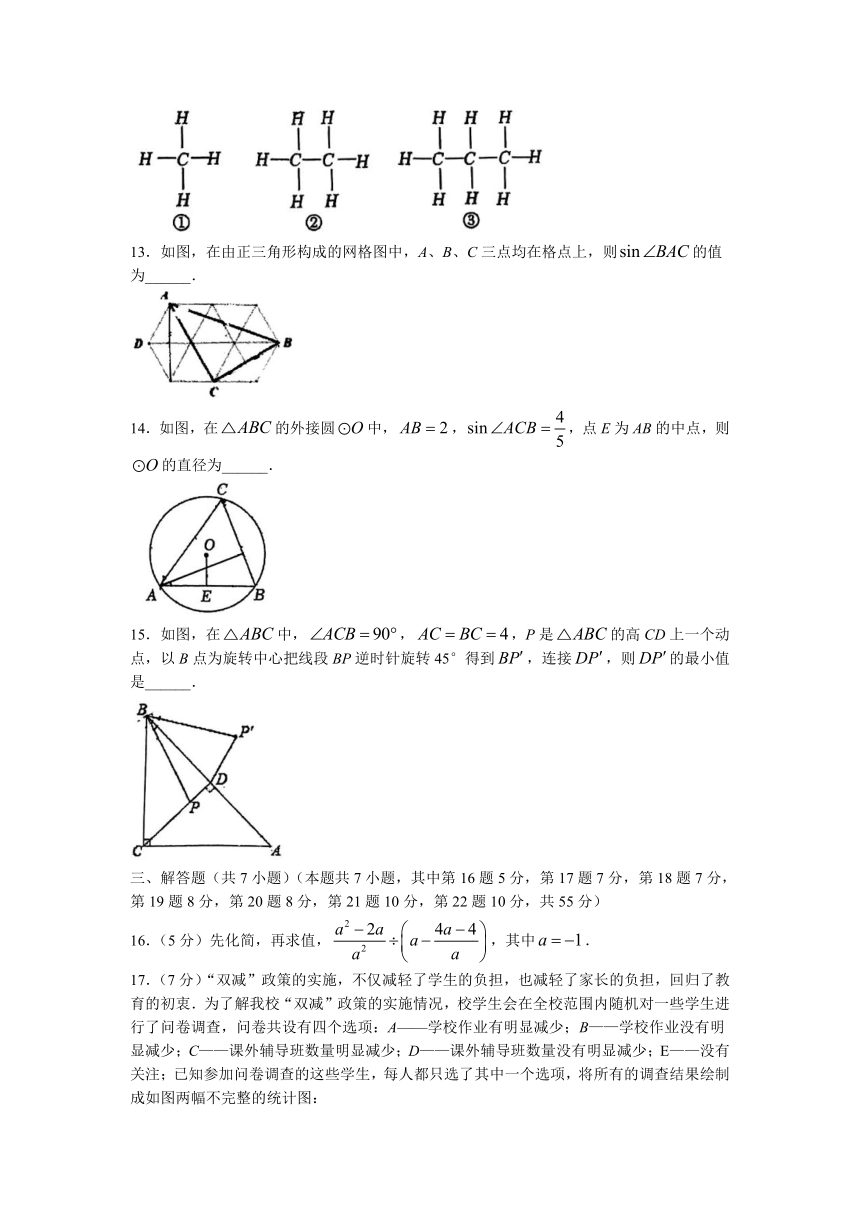
8.下列命题是真命题的是( )
A.相等的两个角是对顶角 B.相等的圆周角所对的弧相等
C.若,则 D.对角线互相平分的四边形是平行四边形
9.如图,在锐角中,,按如下步骤作图.
第一步:作∠BAC的平分线AD;交BC于点D;
第二步:作AD的垂直平分线EF,交AC于点E,交AB于点F;
第三步:连接DE.
则下列结论正确的是( )
A. B. C. D.
10.如图,在平面直角坐标系中,菱形ABCD的边BC与x轴平行,A,B两点纵坐标分别为4,2,反比例函数经过A,B两点,若菱形ABCD面积为8,则k值为( )
A. B. C.-8 D.
二、填空题(共3小题,每小题3分,共15分)
11.分解因式:______.
12.化学中直链烷烃的名称用“碳原子数+烷”来表示。当碳原子数为1~10时,依次用天干——甲、乙、丙、丁、戊、己、庚、辛、千、癸——表示,其中甲烷、乙烷、丙烷的分子结构式如图所示,则第7个庚烷分子结构式中“H”的个数是______.
13.如图,在由正三角形构成的网格图中,A、B、C三点均在格点上,则的值为______.
14.如图,在的外接圆中,,,点E为AB的中点,则的直径为______.
15.如图,在中,,,P是的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到,连接,则的最小值是______.
三、解答题(共7小题)(本题共7小题,其中第16题5分,第17题7分,第18题7分,第19题8分,第20题8分,第21题10分,第22题10分,共55分)
16.(5分)先化简,再求值,,其中.
17.(7分)“双减”政策的实施,不仅减轻了学生的负担,也减轻了家长的负担,回归了教育的初衷.为了解我校“双减”政策的实施情况,校学生会在全校范围内随机对一些学生进行了问卷调查,问卷共设有四个选项:A——学校作业有明显减少;B——学校作业没有明显减少;C——课外辅导班数量明显减少;D——课外辅导班数量没有明显减少;E——没有关注;已知参加问卷调查的这些学生,每人都只选了其中一个选项,将所有的调查结果绘制成如图两幅不完整的统计图:
请你根据以上信息,回答下列问题:
(1)本次接受调查的学生共有______人;______°;______;
(2)补全条形统计图;
(3)该校计划在某个班向家长展示“双减”背景下的课堂教学活动,用于展开活动的备选班级共5个,其中有2个为八年级班级(分别用A、B表示),3个为九年级班级(分别用C、D、E表示),由于报名参加观摩课堂教学活动的家长较多,学校计划分两周进行,第一周先从这5个备选班级中任意选择一个开展活动,第二周再从剩下的四个备选班级中任意选择一个开展活动.请用列表法或画树状图的方法求两次选中的既有)年级班级又有九年级班级的概率.
18.(7分)消防车是救援火灾的主要装备,图①是一辆登高云梯消防车的实物图,图②是其工作示意图,起重臂AC(20米≤AC≤30米)是可伸缩的,且起重臂AC可绕点A在一定范围内上下转动张角,转动点A距离地面的高度AE为4米.
(1)当起重臂AC的长度为24米,张角时,云梯消防车最高点C距离地面的高度CF的长为_____米.
(2)某日一栋大楼突发火灾,着火点距离地面的高度为26米,该消防车在这栋楼下能否实施有效救援?请说明理由(参考数据:)
(提示:当起重臂AC伸到最长且张角∠CAE最大时,云梯顶端C可以达到最大高度)
19.(8分)如图,在中,以边AB为直径作,交AC于点D,点E为边BC上一点,连接DE.给出下列信息:①;②;③DE是的切线.
(1)请在上述3条信息中选择其中两条作为条件,剩下的一条作为结论,组成一个命题.你选择的两个条件是______,结论是______(只要填写序号).判断此命题是否正确,并说明理由;
(2)在(1)的条件下,若,,求的直径.
20.(8分)某种商品的标价为200元/件,由于市场的影响,销量不佳,店家经过两次降价后的价格为128元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为80元/件,若以128元/件售出,平均每天能售出20件,另外每天需支付其他各种费用100元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售出5件,如果每天盈利1475元,每件应降价多少元?
21.(10分)小明同学在探究函数的图象和性质时经历以下几个学习过程:
(I)列表(完成以下表格).
x … -2 -1 0 1 2 3 4 5 6 …
… 15 8 0 0 3 15 …
… 15 8 0 0 3 15 …
(II)描点并画出函数图象草图(在备用图①中描点并画图).
(I)根据图象解决以下问题:
(1)观察图象:函数的图象可由函数的图象如何变化得到?
答:______.
(2)探究发现直线与函数的图象交于点E,F,,,则不等式的解集是______.
(3)设函数的图象与x轴交于A,B两点(B位于A的右侧),与y轴交于点C.
①求直线BC的解析式;
②探究应用:将直线BC沿y轴平移m个单位长度后与函数的图象恰好有3个交点,求此时m的值.
22.(10分)如图,在矩形ABCD中,点E为边AD的中点,点F为AB上的一个动点,连接FE并延长,交CD的延长线于点G,以FG为底边在FG下方作等腰,且.
(1)如图①,若点H恰好落在BC上,连接BE,EH.
①求证:;
②若,,求的面积;
(2)如图②,点H落在矩形ABCD内,连接CH,若,,求四边形FHCB面积的最大值.
九年级数学试卷
一、选择题(共10小题,每小题3分,共30分)
1.-2023的相反数是( )
A.-2023 B.2023 C. D.
2.2022年4月16日,神舟十三号载人飞船圆满完成全部既定任务,顺利返回地球家园.六个月的飞天之旅展现了中国航天科技的新高度.下列航天图标,其图案是中心对称图形的是( )
A.中国探火 B.中国火箭
C.中国行星探测 D.航天神舟
3.2021年是中国共产党建党百年,走过百年光辉历程的中国共产党,成为世界最大的马克思主义执政党.截止2023年6月5日全国共有9518万名中国共产党员,将“9518万”用科学记数法表示应为( )
A. B. C. D.
4.下列运算正确的是( )
A. B.
C. D.
5.神奇的自然界处处蕴含着数学知识.动物学家在鹦鹉螺外壳上发现,其每圈螺纹的直径与相邻螺纹直径的比约为0.618,这体现了数学中的( )
A.平移 B.旋转 C.轴对称 D.黄金分割
6.某小组长统计组内5人一天在课堂上的发言次数分别为3,3,0,4,5.关于这组数据,下列说法错误的是( )
A.众数是3 B.中位数是0 C.平均数是3 D.极差是5
7.光线在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.如图,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且,则( )
A.61° B.58° C.48° D.41°
8.下列命题是真命题的是( )
A.相等的两个角是对顶角 B.相等的圆周角所对的弧相等
C.若,则 D.对角线互相平分的四边形是平行四边形
9.如图,在锐角中,,按如下步骤作图.
第一步:作∠BAC的平分线AD;交BC于点D;
第二步:作AD的垂直平分线EF,交AC于点E,交AB于点F;
第三步:连接DE.
则下列结论正确的是( )
A. B. C. D.
10.如图,在平面直角坐标系中,菱形ABCD的边BC与x轴平行,A,B两点纵坐标分别为4,2,反比例函数经过A,B两点,若菱形ABCD面积为8,则k值为( )
A. B. C.-8 D.
二、填空题(共3小题,每小题3分,共15分)
11.分解因式:______.
12.化学中直链烷烃的名称用“碳原子数+烷”来表示。当碳原子数为1~10时,依次用天干——甲、乙、丙、丁、戊、己、庚、辛、千、癸——表示,其中甲烷、乙烷、丙烷的分子结构式如图所示,则第7个庚烷分子结构式中“H”的个数是______.
13.如图,在由正三角形构成的网格图中,A、B、C三点均在格点上,则的值为______.
14.如图,在的外接圆中,,,点E为AB的中点,则的直径为______.
15.如图,在中,,,P是的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到,连接,则的最小值是______.
三、解答题(共7小题)(本题共7小题,其中第16题5分,第17题7分,第18题7分,第19题8分,第20题8分,第21题10分,第22题10分,共55分)
16.(5分)先化简,再求值,,其中.
17.(7分)“双减”政策的实施,不仅减轻了学生的负担,也减轻了家长的负担,回归了教育的初衷.为了解我校“双减”政策的实施情况,校学生会在全校范围内随机对一些学生进行了问卷调查,问卷共设有四个选项:A——学校作业有明显减少;B——学校作业没有明显减少;C——课外辅导班数量明显减少;D——课外辅导班数量没有明显减少;E——没有关注;已知参加问卷调查的这些学生,每人都只选了其中一个选项,将所有的调查结果绘制成如图两幅不完整的统计图:
请你根据以上信息,回答下列问题:
(1)本次接受调查的学生共有______人;______°;______;
(2)补全条形统计图;
(3)该校计划在某个班向家长展示“双减”背景下的课堂教学活动,用于展开活动的备选班级共5个,其中有2个为八年级班级(分别用A、B表示),3个为九年级班级(分别用C、D、E表示),由于报名参加观摩课堂教学活动的家长较多,学校计划分两周进行,第一周先从这5个备选班级中任意选择一个开展活动,第二周再从剩下的四个备选班级中任意选择一个开展活动.请用列表法或画树状图的方法求两次选中的既有)年级班级又有九年级班级的概率.
18.(7分)消防车是救援火灾的主要装备,图①是一辆登高云梯消防车的实物图,图②是其工作示意图,起重臂AC(20米≤AC≤30米)是可伸缩的,且起重臂AC可绕点A在一定范围内上下转动张角,转动点A距离地面的高度AE为4米.
(1)当起重臂AC的长度为24米,张角时,云梯消防车最高点C距离地面的高度CF的长为_____米.
(2)某日一栋大楼突发火灾,着火点距离地面的高度为26米,该消防车在这栋楼下能否实施有效救援?请说明理由(参考数据:)
(提示:当起重臂AC伸到最长且张角∠CAE最大时,云梯顶端C可以达到最大高度)
19.(8分)如图,在中,以边AB为直径作,交AC于点D,点E为边BC上一点,连接DE.给出下列信息:①;②;③DE是的切线.
(1)请在上述3条信息中选择其中两条作为条件,剩下的一条作为结论,组成一个命题.你选择的两个条件是______,结论是______(只要填写序号).判断此命题是否正确,并说明理由;
(2)在(1)的条件下,若,,求的直径.
20.(8分)某种商品的标价为200元/件,由于市场的影响,销量不佳,店家经过两次降价后的价格为128元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为80元/件,若以128元/件售出,平均每天能售出20件,另外每天需支付其他各种费用100元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售出5件,如果每天盈利1475元,每件应降价多少元?
21.(10分)小明同学在探究函数的图象和性质时经历以下几个学习过程:
(I)列表(完成以下表格).
x … -2 -1 0 1 2 3 4 5 6 …
… 15 8 0 0 3 15 …
… 15 8 0 0 3 15 …
(II)描点并画出函数图象草图(在备用图①中描点并画图).
(I)根据图象解决以下问题:
(1)观察图象:函数的图象可由函数的图象如何变化得到?
答:______.
(2)探究发现直线与函数的图象交于点E,F,,,则不等式的解集是______.
(3)设函数的图象与x轴交于A,B两点(B位于A的右侧),与y轴交于点C.
①求直线BC的解析式;
②探究应用:将直线BC沿y轴平移m个单位长度后与函数的图象恰好有3个交点,求此时m的值.
22.(10分)如图,在矩形ABCD中,点E为边AD的中点,点F为AB上的一个动点,连接FE并延长,交CD的延长线于点G,以FG为底边在FG下方作等腰,且.
(1)如图①,若点H恰好落在BC上,连接BE,EH.
①求证:;
②若,,求的面积;
(2)如图②,点H落在矩形ABCD内,连接CH,若,,求四边形FHCB面积的最大值.
同课章节目录
